Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T15:04:53.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On the limiting distribution of the failure time of fibrous materials

Published online by Cambridge University Press:  01 July 2016

Wagner De Souza Borges
Wagner De Souza Borges*
Affiliation:
Universidade de São Paulo
*
∗Postal address: Instituto de Matemática e Estatistica, Universidade de São Paulo, Caixa Postal 20570, Ag lguatemi, 05508 São Paulo SP, Brazil.
Get access Rights & Permissions [Opens in a new window]

Abstract

A large deviation theorem of the Cramér–Petrov type and a ranking limit theorem of Loève are used to derive an approximation for the statistical distribution of the failure time of fibrous materials. For that, fibrous materials are modeled as a series of independent and identical bundles of parallel filaments and the asymptotic distribution of their failure time is determined in terms of statistical characteristics of the individual filaments, as both the number of filaments in each bundle and the number of bundles in the chain grow large simultaneously. While keeping the number n of filaments in each bundle fixed and increasing only the chain length k leads to a Weibull limiting distribution for the failure time, letting both increase in such a way that log k(n) = o(n), we show that the limit distribution is 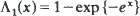for 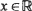. Since fibrous materials which are both long and have many filaments prevail, the result is of importance in the materials science area since refined approximations to failure-time distributions can be achieved.

Keywords

MECHANICAL SYSTEMSFIBER BUNDLESRELIABILITYLIFE DISTRIBUTION
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 2 , June 1983 , pp. 331 - 348
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partly carried out while the author was visiting the University of Pittsburgh.

Supported in part by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), processo n°. 200175-81.

References

Book, S. (1976) The Cramér-Feller-Petrov large deviation theorem for triangular arrays. Unpublished report.Google Scholar
Borges, W. S. (1978) Extreme Value Theory in Triangular Arrays with an Application to the Reliability of Fibrous Materials. Ph.D. Dissertation, Department of Operations Research, Cornell University.Google Scholar
Coleman, B. D. (1957) Time dependence of mechanical breakdown in bundles of fibres I. Constant total load. J. Appl. Phys. 28, 1058–1064.Google Scholar
Coleman, B. D. (1958) Time dependence of mechanical breakdown in bundles of fibers III. The power law breakdwon rule. Trans. Soc. Rheol. 2, 195–218.Google Scholar
Daniels, H. E. (1945) The statistical theory of the strength of bundles of threads, I. Proc. R. Soc. London A 183, 403–435.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Gnedenko, B. V. (1946) Sur la distribution limite du terme maximum d'une série aléatoire. Ann. Math. 44, 423–453.Google Scholar
Harlow, D. G. (1977) Probabilistic Models for the Tensile Strength of Composite Materials. , Department of Operations Research, Cornell University.Google Scholar
Harlow, D. G. and Phoenix, S. L. (1978) The chain-of-bundles model for the strength of fibrous materials I. J. Composite Materials 12, 195–214.CrossRefGoogle Scholar
Harlow, D. G., Smith, R. and Taylor, H. M. (1978) The asymptotic distribution of certain long composite cables. Technical Report 384, Department of Operations Research, Cornell University.Google Scholar
Ivchenko, G. I. (1973) Variational series for a scheme of summing independent variables. Theory Prob. Appl. 18, 531–545.Google Scholar
Loeve, M. (1956) Ranking limit problem. Proc. 3rd Berkeley Symp. Math. Statist. Prob. 2, 177–194.Google Scholar
Phoenix, S. L. (1978) The asymptotic time to failure of a mechanical system of parallel members. SIAM J. Appl. Math. 34, 227–246.CrossRefGoogle Scholar
Phoenix, S. L. (1979) The asymptotic distribution for the time to failure of a fibre bundle. Adv. Appl. Prob. 11, 153–187.CrossRefGoogle Scholar
Phoenix, S. L. and Taylor, H. M. (1973) Asymptotic strength distribution of a general fiber bundle. Adv. Appl. Prob. 5, 200–216.CrossRefGoogle Scholar
Rudin, W. (1966) Real and Complex Analysis. McGraw-Hill, New York.Google Scholar
Smirnov, N. V. (1952) Limit distributions for the terms of a variational series. Amer. Math. Soc. Transl. 67, 1–64.Google Scholar
Smith, R. (1982) The asymptotic distribution of the strength of a series-parallel system with equal load sharing. Ann. Prob. 10, 137–171.CrossRefGoogle Scholar
Statulevicius, V. (1966) On large deviations. Z. Wahrscheinlichkeitsth. 6, 133–144.Google Scholar
Suh, W. M., Bhattacharyya, B. B. and Grand Age, A. (1970) On the distribution and moments of the strength of a bundle of filaments. J. Appl. Prob. 7, 712–720.Google Scholar