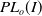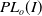1. Introduction
The notion of a girth for a finitely generated group was first introduced in [Reference Schleimer14] motivated by the study of Heegaard splittings of closed 3-manifolds.
Definition 1.1.
Let
![]() $\Gamma$
be a finitely generated group. For any finite generating set
$\Gamma$
be a finitely generated group. For any finite generating set
![]() $S$
of
$S$
of
![]() $\Gamma$
,
$\Gamma$
,
![]() $girth (\Gamma, S)$
will denote the minimal length of relations among the elements of
$girth (\Gamma, S)$
will denote the minimal length of relations among the elements of
![]() $S$
. Then, we define
$S$
. Then, we define
By definition above, an infinite cyclic group has infinite girth, but this fact should be viewed as a degeneracy since (as remarked in [Reference Akhmedov1]) any group satisfying a law and non-isomorphic to
![]() $\mathbb{Z}$
has a finite girth.
$\mathbb{Z}$
has a finite girth.
In [Reference Akhmedov2], we have proved that if a finitely generated group is word hyperbolic, or one-relator, or linear then it is either virtually solvable or has infinite girth. More generally, given a class
![]() $\mathcal{C}$
of finitely generated groups, we will say that
$\mathcal{C}$
of finitely generated groups, we will say that
![]() $\mathcal{C}$
satisfies the Girth Alternative if any group from the class
$\mathcal{C}$
satisfies the Girth Alternative if any group from the class
![]() $\mathcal{C}$
is either virtually solvable or has infinite girth.
$\mathcal{C}$
is either virtually solvable or has infinite girth.
In [Reference Yamagata15], S. Yamagata has proved the Girth Alternative for convergence groups and for irreducible subgroups of mapping class groups. Independently, in [Reference Nakamura12] and [Reference Nakamura13], K. Nakamura proves the alternative for convergence groups but also for all subgroups of mapping class groups as well as for subgroups of
![]() $Out(\mathbb{F}_n)$
that contain irreducible elements with irreducible powers.
$Out(\mathbb{F}_n)$
that contain irreducible elements with irreducible powers.
In this paper, we will prove that the Girth Alternative holds for subgroups of
![]() $PL_o(I)$
—the group of orientation-preserving piecewise linear homeomorphisms of the closed interval
$PL_o(I)$
—the group of orientation-preserving piecewise linear homeomorphisms of the closed interval
![]() $I = [0,1]$
. It is known that any virtually solvable subgroup of
$I = [0,1]$
. It is known that any virtually solvable subgroup of
![]() $PL_o(I)$
is indeed solvable (see [Reference Bleak7], Corollary 1.3.), so the Girth Alternative in this case is equivalent to the following:
$PL_o(I)$
is indeed solvable (see [Reference Bleak7], Corollary 1.3.), so the Girth Alternative in this case is equivalent to the following:
Theorem 1.2.
Any finitely generated subgroup of
![]() $PL_o(I)$
is either solvable or has infinite girth.
$PL_o(I)$
is either solvable or has infinite girth.
It is remarked in [Reference Akhmedov1] that a finitely generated noncyclic group which satisfies a law has a finite girth. Thus, we obtain the following corollary.
Corollary 1.3.
If a subgroup of
![]() $PL_o(I)$
satisfies a law then it is solvable.
$PL_o(I)$
satisfies a law then it is solvable.
Remark 1.4.
As another corollary of Theorem
1.2
, we obtain that
![]() $girth (F) = \infty$
where
$girth (F) = \infty$
where
![]() $F$
denotes the R.Thompson’s group. This fact has been proved in [Reference Brin9] and in [Reference Akhmedov, Stein and Taback4]; both proofs use different ideas from each other and from the proof of Theorem
1.2
. Theorem
1.2
also implies that
$F$
denotes the R.Thompson’s group. This fact has been proved in [Reference Brin9] and in [Reference Akhmedov, Stein and Taback4]; both proofs use different ideas from each other and from the proof of Theorem
1.2
. Theorem
1.2
also implies that
![]() $girth(B) = \infty$
where
$girth(B) = \infty$
where
![]() $B$
is the Brin group introduced in [Reference Brin10] under the notation
$B$
is the Brin group introduced in [Reference Brin10] under the notation
![]() $G_1$
(the notation
$G_1$
(the notation
![]() $B$
is used in [Reference Bleak7] and in [Reference Dranishnikov and Sapir11], among other places).
$B$
is used in [Reference Bleak7] and in [Reference Dranishnikov and Sapir11], among other places).
It is easy to prove the Girth Alternative for Diff
![]() $_{\omega }(I)$
—the group of orientation-preserving analytic diffeomorphisms of
$_{\omega }(I)$
—the group of orientation-preserving analytic diffeomorphisms of
![]() $I$
, however, we do not know if the alternative still holds when the regularity is decreased. The following questions are interesting to us:
$I$
, however, we do not know if the alternative still holds when the regularity is decreased. The following questions are interesting to us:
Question 1. Does Girth Alternative hold for subgroups
(a) of Homeo
![]() $_{+}(I)$
? (b) of Diff
$_{+}(I)$
? (b) of Diff
![]() $_{+}(I)$
?
$_{+}(I)$
?
Question 2. Footnote 1 Is there a finitely generated subgroup of
![]() $PL_o(I)$
which is not embeddable into Diff
$PL_o(I)$
which is not embeddable into Diff
![]() $_{+}(I)$
?
$_{+}(I)$
?
In regard to Question 1, we prove the following partial result.
Theorem 1.5.
Let
![]() $\Gamma$
be any finitely generated subgroup of Homeo
$\Gamma$
be any finitely generated subgroup of Homeo
![]() $_{+}(I)$
. Assume that for all
$_{+}(I)$
. Assume that for all
![]() $N\in \mathbb{N}$
, for every sequence
$N\in \mathbb{N}$
, for every sequence
![]() $0 \lt x_1 \lt x_2 \lt \cdots \lt x_N \lt 1$
, and for all
$0 \lt x_1 \lt x_2 \lt \cdots \lt x_N \lt 1$
, and for all
![]() $\epsilon \gt 0$
, one can find an element
$\epsilon \gt 0$
, one can find an element
![]() $\gamma \in \Gamma$
such that
$\gamma \in \Gamma$
such that
![]() $Fix(\gamma ) = \{0, c_1, \ldots, c_N, 1\}$
, and
$Fix(\gamma ) = \{0, c_1, \ldots, c_N, 1\}$
, and
![]() $|c_i-x_i| \lt \epsilon$
, for all
$|c_i-x_i| \lt \epsilon$
, for all
![]() $1\leq i\leq N$
. Then
$1\leq i\leq N$
. Then
![]() $girth (\Gamma ) = \infty$
.
$girth (\Gamma ) = \infty$
.
Remark 1.6.
As a corollary of Theorem
1.5
, we obtain yet another proof of the fact that
![]() $girth (F) = \infty$
.
$girth (F) = \infty$
.
At the end of this section, let us also note that the core of the ideas in our proofs (more visibly in the proof of Theorem 1.5) aligns with (and can be viewed as a case of) the method of “fast generating sets” which has been developed systematically in [Reference Bleak, Brin, Kassabov, Moore and Zaremsky5]. In [Reference Bleak, Brin and Moorie6], the authors exploit this method to build elementary amenable subgroups of
![]() $PL_o(I)$
with very complex EA class.
$PL_o(I)$
with very complex EA class.
2. Towers and exemplary towers: review of Collin Bleak’s results
In the proof of Theorem 1.2, as a crucial tool, we use the result of C. Bleak on the existence of arbitrarily high towers in a non-solvable subgroup of
![]() $PL_o(I)$
, [Reference Bleak7]. First, we would like to introduce the following notions essentially borrowed from [Reference Bleak7], with a slightly different terminology.
$PL_o(I)$
, [Reference Bleak7]. First, we would like to introduce the following notions essentially borrowed from [Reference Bleak7], with a slightly different terminology.
Definition 2.1.
An ordered
![]() $n$
-tuple
$n$
-tuple
![]() $(f_1, \ldots, f_n)$
of elements of
$(f_1, \ldots, f_n)$
of elements of
![]() $PL_o(I)$
is said to form a strict tower if there exist intervals
$PL_o(I)$
is said to form a strict tower if there exist intervals
![]() $(a_i, b_i), 1\leq i\leq n$
such that
$(a_i, b_i), 1\leq i\leq n$
such that
-
(i)
 $0 \lt a_1 \lt \ldots \lt a_n \lt b_n \lt \ldots \lt b_1 \lt 1$
;
$0 \lt a_1 \lt \ldots \lt a_n \lt b_n \lt \ldots \lt b_1 \lt 1$
; -
(ii) for all
 $i\in \{1, \ldots, n\}, \ f_i(a_i) = a_i, f(b_i) = b_i$
, and
$i\in \{1, \ldots, n\}, \ f_i(a_i) = a_i, f(b_i) = b_i$
, and
 $f_i$
has no fixed points in
$f_i$
has no fixed points in
 $(a_i, b_i)$
.
$(a_i, b_i)$
. -
(iii) for all
 $i, j\in \{1, \ldots, n\}$
, if
$i, j\in \{1, \ldots, n\}$
, if
 $i \lt j$
then
$i \lt j$
then
 $f_i(x) \gt f_j(x), \forall x\in [a_j,b_j]$
$f_i(x) \gt f_j(x), \forall x\in [a_j,b_j]$
We will denote the strict tower by
![]() $T = [(f_1, \ldots, f_n);\; (a_1,b_1), \ldots, (a_n, b_n)]$
;
$T = [(f_1, \ldots, f_n);\; (a_1,b_1), \ldots, (a_n, b_n)]$
;
![]() $n$
will be called the height of the tower
$n$
will be called the height of the tower
![]() $T$
, and the interval
$T$
, and the interval
![]() $(a_i, b_i)$
will be called the
$(a_i, b_i)$
will be called the
![]() $i$
-th base of the tower.
$i$
-th base of the tower.
Definition 2.2. We will say that a strict tower
is suitable if for any nonzero integer
![]() $p$
and for all
$p$
and for all
![]() $1\leq i \lt j \leq n$
, the following condition holds:
$1\leq i \lt j \leq n$
, the following condition holds:
![]() $ f_i^p([a_j,b_j])\cap \displaystyle \mathop{\cup }_{i+1\leq k\leq n} supp (f_k) = \emptyset \ (1)$
.
$ f_i^p([a_j,b_j])\cap \displaystyle \mathop{\cup }_{i+1\leq k\leq n} supp (f_k) = \emptyset \ (1)$
.
Remark 2.3.
Condition (1) of Definition 2.2 implies that for any nonzero integer
![]() $p$
and for all
$p$
and for all
![]() $1\,{\leq}\, i\,{\lt}\, j\, {\leq}\, n$
,
$1\,{\leq}\, i\,{\lt}\, j\, {\leq}\, n$
,
![]() $ f_i^p([a_j,b_j])\cap [a_j,b_j] = \emptyset \ (2)$
. Notice that, if the
$ f_i^p([a_j,b_j])\cap [a_j,b_j] = \emptyset \ (2)$
. Notice that, if the
![]() $n$
-tuple
$n$
-tuple
![]() $(f_1, \ldots, f_n)$
of elements of
$(f_1, \ldots, f_n)$
of elements of
![]() $PL_o(I)$
forms a tower then for sufficiently big
$PL_o(I)$
forms a tower then for sufficiently big
![]() $q\in \mathbb{N}$
, the
$q\in \mathbb{N}$
, the
![]() $n$
-tuple
$n$
-tuple
![]() $(f_1^q, \ldots, f_n^q)$
forms a tower with the same bases which satisfies condition
$(f_1^q, \ldots, f_n^q)$
forms a tower with the same bases which satisfies condition
![]() $(2)$
. Also, the existence of a suitable tower of arbitrary height in non-solvable subgroups of
$(2)$
. Also, the existence of a suitable tower of arbitrary height in non-solvable subgroups of
![]() $PL_o(I)$
immediately follows from the existence of the exemplary towers of arbitrary height, [Reference Bleak7].
$PL_o(I)$
immediately follows from the existence of the exemplary towers of arbitrary height, [Reference Bleak7].
To explain the existence of exemplary towers, we would like to make a digression into some of the results of C. Bleak. For the rest of this section, let
![]() $\Gamma \leq PL_o(I)$
. The following notions and notations are all borrowed directly from [Reference Bleak7].
$\Gamma \leq PL_o(I)$
. The following notions and notations are all borrowed directly from [Reference Bleak7].
We will call the convex hull of a point in
![]() $I$
under the action of
$I$
under the action of
![]() $\Gamma$
an orbital of
$\Gamma$
an orbital of
![]() $\Gamma$
, if this convex hull contains more than one point. We note that the orbitals are open intervals. If
$\Gamma$
, if this convex hull contains more than one point. We note that the orbitals are open intervals. If
![]() $g\in \Gamma$
, we will refer to an orbital of the group
$g\in \Gamma$
, we will refer to an orbital of the group
![]() $\langle g \rangle$
as an orbital of
$\langle g \rangle$
as an orbital of
![]() $g$
. If an open interval
$g$
. If an open interval
![]() $A$
is an orbital of
$A$
is an orbital of
![]() $g$
, then the pair
$g$
, then the pair
![]() $(A,g)$
will be called a signed orbital of
$(A,g)$
will be called a signed orbital of
![]() $G$
.
$G$
.
![]() $g$
will be called the signature of the signed orbital
$g$
will be called the signature of the signed orbital
![]() $(A,g)$
.
$(A,g)$
.
Given a set
![]() $Y$
of signed orbitals of
$Y$
of signed orbitals of
![]() $G$
, the symbol
$G$
, the symbol
![]() $S_Y$
will refer to the set of signatures of the signed orbitals in
$S_Y$
will refer to the set of signatures of the signed orbitals in
![]() $Y$
. Similarly, the symbol
$Y$
. Similarly, the symbol
![]() $O_Y$
will refer to the set of orbitals of the signed orbitals of
$O_Y$
will refer to the set of orbitals of the signed orbitals of
![]() $Y$
. We note that the set of signed orbitals of
$Y$
. We note that the set of signed orbitals of
![]() $PL_o(I)$
is a partially ordered set under the lexicographic order induced from the partial order on subsets of
$PL_o(I)$
is a partially ordered set under the lexicographic order induced from the partial order on subsets of
![]() $I$
(induced by inclusion) in the first coordinate, and the left total order of the elements of
$I$
(induced by inclusion) in the first coordinate, and the left total order of the elements of
![]() $PL_o(I)$
in the second coordinate.
$PL_o(I)$
in the second coordinate.
A tower
![]() $T$
of
$T$
of
![]() $G$
is a set of signed orbitals which satisfies the following two criteria.
$G$
is a set of signed orbitals which satisfies the following two criteria.
-
1.
 $T$
is a chain in the partial order on the signed orbitals of
$T$
is a chain in the partial order on the signed orbitals of
 $G$
.
$G$
. -
2. For any
 $A\in O_T$
,
$A\in O_T$
,
 $T$
has exactly one element of the form
$T$
has exactly one element of the form
 $(A,g)$
.
$(A,g)$
.
Given a tower
![]() $T$
of
$T$
of
![]() $G$
, if
$G$
, if
![]() $(A,g), (B,h)\in T$
then one of
$(A,g), (B,h)\in T$
then one of
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $B\subseteq A$
holds, with equality occurring only if
$B\subseteq A$
holds, with equality occurring only if
![]() $g = h$
as well. Therefore, one can visualize the tower as a stack of nested levels that are always getting wider as one goes “up” the stack.
$g = h$
as well. Therefore, one can visualize the tower as a stack of nested levels that are always getting wider as one goes “up” the stack.
The cardinality of the set
![]() $O_T$
will be called the height of the tower
$O_T$
will be called the height of the tower
![]() $T$
. Besides the cardinality, we also want to make use of the order structure of towers which allows to define the following more sensitive notions: if there is an order-preserving injection from
$T$
. Besides the cardinality, we also want to make use of the order structure of towers which allows to define the following more sensitive notions: if there is an order-preserving injection from
![]() ${\mathbb{N}}$
to
${\mathbb{N}}$
to
![]() $T$
, then we will say
$T$
, then we will say
![]() $T$
is tall, and if there is an order-preserving injection from
$T$
is tall, and if there is an order-preserving injection from
![]() $-{\mathbb{N}}$
to
$-{\mathbb{N}}$
to
![]() $T$
, then we will say
$T$
, then we will say
![]() $T$
is deep. If
$T$
is deep. If
![]() $T$
is both deep and tall, then we will say
$T$
is both deep and tall, then we will say
![]() $T$
is a bi-infinite tower; in the latter case, there will be an order-preserving injection from
$T$
is a bi-infinite tower; in the latter case, there will be an order-preserving injection from
![]() ${\mathbb{Z}}$
to
${\mathbb{Z}}$
to
![]() $T$
.
$T$
.
A major result of [Reference Bleak7] is the following beautiful geometric characterization of solvable subgroups of
![]() $PL_o(I)$
.
$PL_o(I)$
.
Theorem 2.4.
If
![]() $G\leq PL_o(I)$
is a non-solvable subgroup if and only if
$G\leq PL_o(I)$
is a non-solvable subgroup if and only if
![]() $G$
admits a tower of height
$G$
admits a tower of height
![]() $n$
for any
$n$
for any
![]() $n\geq 1$
.
$n\geq 1$
.
If
![]() $G$
admits two signed orbitals
$G$
admits two signed orbitals
![]() $(A,g)$
and
$(A,g)$
and
![]() $(B,h)$
so that
$(B,h)$
so that
![]() $A = (a_1,a_2)$
and
$A = (a_1,a_2)$
and
![]() $B = (b_1, b_2)$
, with
$B = (b_1, b_2)$
, with
![]() $a_1 \lt b_1 \lt a_2 \lt b_2$
then we will say that
$a_1 \lt b_1 \lt a_2 \lt b_2$
then we will say that
![]() $G$
admits a transition chain of length two. One can similarly define transition chains of any (finite) length, but we will have no need for that generality here.
$G$
admits a transition chain of length two. One can similarly define transition chains of any (finite) length, but we will have no need for that generality here.
If
![]() $A = (a,b)$
is an orbital of the group
$A = (a,b)$
is an orbital of the group
![]() $G$
, and
$G$
, and
![]() $G$
has an element
$G$
has an element
![]() $g$
which has an orbital
$g$
which has an orbital
![]() $B = (c,d)$
so that either
$B = (c,d)$
so that either
![]() $c = a$
or
$c = a$
or
![]() $d = b$
, then we say that
$d = b$
, then we say that
![]() $g$
has an orbital that shares an end with
$g$
has an orbital that shares an end with
![]() $A$
.
$A$
.
Given an orbital
![]() $A$
of
$A$
of
![]() $H$
, we say that
$H$
, we say that
![]() $h$
realizes an end of
$h$
realizes an end of
![]() $A$
if some orbital of
$A$
if some orbital of
![]() $h$
lies entirely in
$h$
lies entirely in
![]() $A$
and shares an end with
$A$
and shares an end with
![]() $A$
. If
$A$
. If
![]() $g$
and
$g$
and
![]() $h$
are elements of
$h$
are elements of
![]() $PL_o(I)$
and there is an interval
$PL_o(I)$
and there is an interval
![]() $B = (a,b)\subset I$
so that both
$B = (a,b)\subset I$
so that both
![]() $g$
and
$g$
and
![]() $h$
have
$h$
have
![]() $B$
as an orbital, then we will say that
$B$
as an orbital, then we will say that
![]() $g$
and
$g$
and
![]() $h$
share the orbital
$h$
share the orbital
![]() $B$
.
$B$
.
We will say that an orbital
![]() $A$
of a group
$A$
of a group
![]() $H\leq PL_o(I)$
is imbalanced if some element
$H\leq PL_o(I)$
is imbalanced if some element
![]() $h\in H$
realizes one end of
$h\in H$
realizes one end of
![]() $A$
, but not the other, and we will say
$A$
, but not the other, and we will say
![]() $A$
is balanced if whenever an element
$A$
is balanced if whenever an element
![]() $h\in H$
realizes one end of
$h\in H$
realizes one end of
![]() $A$
, then
$A$
, then
![]() $h$
also realizes the other end of
$h$
also realizes the other end of
![]() $A$
(note that
$A$
(note that
![]() $h$
might do this with two distinct orbitals). A subgroup
$h$
might do this with two distinct orbitals). A subgroup
![]() $H\leq PL_o(I)$
will be called balanced if given any subgroup
$H\leq PL_o(I)$
will be called balanced if given any subgroup
![]() $G\leq H$
, and any orbital
$G\leq H$
, and any orbital
![]() $A$
of
$A$
of
![]() $G$
, every element of
$G$
, every element of
![]() $G$
which realizes one end of
$G$
which realizes one end of
![]() $A$
also realizes the other end of
$A$
also realizes the other end of
![]() $A$
. In the case where
$A$
. In the case where
![]() $H$
has a subgroup
$H$
has a subgroup
![]() $G$
with an imbalanced orbital, then we will say that
$G$
with an imbalanced orbital, then we will say that
![]() $H$
is imbalanced.
$H$
is imbalanced.
We say a tower
![]() $T$
is an exemplary tower if the following two additional properties hold:
$T$
is an exemplary tower if the following two additional properties hold:
-
1. Whenever
 $(A,g), (B,h)\in T$
then
$(A,g), (B,h)\in T$
then
 $(A,g)\leq (B,h)$
implies the orbitals of
$(A,g)\leq (B,h)$
implies the orbitals of
 $g$
are disjoint from both ends of the orbital
$g$
are disjoint from both ends of the orbital
 $B$
.
$B$
. -
2. Whenever
 $(A, g), (B, h)\in T$
then
$(A, g), (B, h)\in T$
then
 $(A,g)\leq (B,h)$
implies no orbital of
$(A,g)\leq (B,h)$
implies no orbital of
 $g$
in
$g$
in
 $B$
shares an end with
$B$
shares an end with
 $B$
.
$B$
.
C. Bleak proves several technical results which indicate the plethora of exemplary towers in
![]() $PL_o(I)$
. The following two lemmas are stated in [Reference Bleak7] as Lemmas 1.4 and 2.12, respectively.
$PL_o(I)$
. The following two lemmas are stated in [Reference Bleak7] as Lemmas 1.4 and 2.12, respectively.
Lemma 2.5.
If
![]() $H$
is a subgroup of
$H$
is a subgroup of
![]() $PL_o(I)$
, and
$PL_o(I)$
, and
![]() $H$
admits a transition chain of length two, then
$H$
admits a transition chain of length two, then
![]() $H$
admits infinite towers.
$H$
admits infinite towers.
Lemma 2.6.
If
![]() $H$
is a subgroup of
$H$
is a subgroup of
![]() $PL_o(I)$
which does not admit a transition chain of length two and
$PL_o(I)$
which does not admit a transition chain of length two and
![]() $H$
has a tower
$H$
has a tower
![]() $T$
, then
$T$
, then
![]() $T$
is exemplary.
$T$
is exemplary.
Thus, the existence of a transition chain of length two implies the existence of infinite towers, and the absence of the transition chain of length two implies that all towers are nice, that is, exemplary. It turns out the absence of a transition chain of length two also implies certain nice properties of the group itself. The following result is stated as Remark 4.9 in [Reference Bleak7].
Lemma 2.7.
If
![]() $G$
is a subgroup of
$G$
is a subgroup of
![]() $PL_o(I)$
that does not admit transition chains of length two, then
$PL_o(I)$
that does not admit transition chains of length two, then
![]() $G$
is balanced.
$G$
is balanced.
We also need the following two technical results from [Reference Bleak7].
Lemma 2.8 (Corollary 2.13, [Reference Bleak7]). If
![]() $G$
is a balanced subgroup of
$G$
is a balanced subgroup of
![]() $PL_o(I)$
and
$PL_o(I)$
and
![]() $G$
admits a tall tower in some orbital
$G$
admits a tall tower in some orbital
![]() $A$
, or
$A$
, or
![]() $G$
admits a deep tower in some orbital
$G$
admits a deep tower in some orbital
![]() $A$
, or
$A$
, or
![]() $G$
admits a bi-infinite tower in some orbital
$G$
admits a bi-infinite tower in some orbital
![]() $A$
, then
$A$
, then
![]() $G$
admits an exemplary tall tower in
$G$
admits an exemplary tall tower in
![]() $A$
, or
$A$
, or
![]() $G$
admits an exemplary deep tower in
$G$
admits an exemplary deep tower in
![]() $A$
, or
$A$
, or
![]() $G$
admits an exemplary bi-infinite tower in
$G$
admits an exemplary bi-infinite tower in
![]() $A$
, respectively.
$A$
, respectively.
Lemma 2.9 (Lemma 2.8, [Reference Bleak7]). Suppose
![]() $H\leq PL_o(I)$
, and that
$H\leq PL_o(I)$
, and that
![]() $G\leq H$
has an imbalanced orbital
$G\leq H$
has an imbalanced orbital
![]() $A = (a,b)$
. Then
$A = (a,b)$
. Then
![]() $H$
admits an exemplary bi-infinite tower
$H$
admits an exemplary bi-infinite tower
![]() $E$
whose orbitals are all in
$E$
whose orbitals are all in
![]() $A$
.
$A$
.
Corollary 2.10.
If
![]() $H$
is an imbalanced subgroup of
$H$
is an imbalanced subgroup of
![]() $PL_o(I)$
, then
$PL_o(I)$
, then
![]() $H$
admits an exemplary bi-infinite tower.
$H$
admits an exemplary bi-infinite tower.
Combining the above results we can now claim the following lemma.
Lemma 2.11.
If
![]() $\Gamma \leq PL_o(I)$
is not solvable, then it contains an exemplary tower of any height
$\Gamma \leq PL_o(I)$
is not solvable, then it contains an exemplary tower of any height
![]() $n\geq 1$
.
$n\geq 1$
.
Proof. If
![]() $\Gamma$
does not admit a transition chain of length two, then the claim follows from Theorem 2.4 and Lemma 2.6. If
$\Gamma$
does not admit a transition chain of length two, then the claim follows from Theorem 2.4 and Lemma 2.6. If
![]() $\Gamma$
is not balanced then the claim follows from Corollary 2.10. Thus, we can assume that
$\Gamma$
is not balanced then the claim follows from Corollary 2.10. Thus, we can assume that
![]() $\Gamma$
is balanced and admits a transition chain of length two. Then by Lemma 2.5,
$\Gamma$
is balanced and admits a transition chain of length two. Then by Lemma 2.5,
![]() $\Gamma$
admits an infinite tower. Then by Lemma 2.8, it admits an exemplary bi-infinite tower.
$\Gamma$
admits an infinite tower. Then by Lemma 2.8, it admits an exemplary bi-infinite tower.
3. Proof of Theorem 1.2
For any natural number
![]() $r$
, let
$r$
, let
![]() $G_r = (\ldots ((\mathbb{Z}\wr \mathbb{Z})\wr \mathbb{Z})\wr \ldots \mathbb{Z})\wr \mathbb{Z}$
where the iterated wreath product is taken
$G_r = (\ldots ((\mathbb{Z}\wr \mathbb{Z})\wr \mathbb{Z})\wr \ldots \mathbb{Z})\wr \mathbb{Z}$
where the iterated wreath product is taken
![]() $r$
times. The group
$r$
times. The group
![]() $G_r$
can be defined inductively as
$G_r$
can be defined inductively as
![]() $G_0 = 1, G_{i+1} = G_i\wr \mathbb{Z} \;:\!=\; \mathbb{Z}\ltimes \displaystyle \mathop{\oplus }_{n\in \mathbb{Z}}G_i, 0\leq i\leq r-1$
. In the wreath product
$G_0 = 1, G_{i+1} = G_i\wr \mathbb{Z} \;:\!=\; \mathbb{Z}\ltimes \displaystyle \mathop{\oplus }_{n\in \mathbb{Z}}G_i, 0\leq i\leq r-1$
. In the wreath product
![]() $G_i\wr \mathbb{Z}$
, the standard generator of the acting group
$G_i\wr \mathbb{Z}$
, the standard generator of the acting group
![]() $\mathbb{Z}$
will be denoted by
$\mathbb{Z}$
will be denoted by
![]() $g_{r-i}$
. (in [Reference Bleak7], the group
$g_{r-i}$
. (in [Reference Bleak7], the group
![]() $G_r$
is denoted by
$G_r$
is denoted by
![]() $W_r$
).
$W_r$
).
The following lemma will be useful; the idea of its proof is essentially borrowed from the proof of Lemma 2.3 in [Reference Akhmedov1].
Lemma 3.1.
For all
![]() $q, k\in \mathbb{N}$
, there exist
$q, k\in \mathbb{N}$
, there exist
![]() $r\in \mathbb{N}$
and
$r\in \mathbb{N}$
and
![]() $w_1, \ldots, w_k\in G_r$
such that there is no relation of length less than
$w_1, \ldots, w_k\in G_r$
such that there is no relation of length less than
![]() $q$
among
$q$
among
![]() $w_1, \ldots, w_k$
.
$w_1, \ldots, w_k$
.
Proof. Since a free group on two generators contains a free group on
![]() $k$
generators for any
$k$
generators for any
![]() $k\geq 3$
, it is sufficient to prove the claim for
$k\geq 3$
, it is sufficient to prove the claim for
![]() $k=2$
. We will do this by induction; more precisely, it suffices to prove the following claim: if
$k=2$
. We will do this by induction; more precisely, it suffices to prove the following claim: if
![]() $A, B$
are nontrivial groups and
$A, B$
are nontrivial groups and
![]() $A$
satisfies no law in two variables of length less than
$A$
satisfies no law in two variables of length less than
![]() $n\geq 4$
, then the wreath product
$n\geq 4$
, then the wreath product
![]() $B\wr A = A\ltimes \displaystyle \mathop{\oplus }_{i\in A}B$
satisfies no law in two variables of length less than
$B\wr A = A\ltimes \displaystyle \mathop{\oplus }_{i\in A}B$
satisfies no law in two variables of length less than
![]() $n+1$
.
$n+1$
.
Indeed, let
![]() $w_1, w_2\in A$
with no relation of length less than
$w_1, w_2\in A$
with no relation of length less than
![]() $n$
. An element of
$n$
. An element of
![]() $\displaystyle \mathop{\oplus }_{i\in A}B$
can be written as
$\displaystyle \mathop{\oplus }_{i\in A}B$
can be written as
![]() $(x_g)_{g\in A}$
where all but finitely many “coordinates” are 1. Let
$(x_g)_{g\in A}$
where all but finitely many “coordinates” are 1. Let
![]() $b$
be a non-identity element of
$b$
be a non-identity element of
![]() $B$
, and
$B$
, and
![]() $t = (x_g)_{g\in A}$
be the element of
$t = (x_g)_{g\in A}$
be the element of
![]() $\displaystyle \mathop{\oplus }_{i\in A}B$
where
$\displaystyle \mathop{\oplus }_{i\in A}B$
where
![]() $x_g = b$
for
$x_g = b$
for
![]() $g=1$
and
$g=1$
and
![]() $x_g = 1$
otherwise.
$x_g = 1$
otherwise.
Then there is no relation of length less than
![]() $n+1$
among the elements
$n+1$
among the elements
![]() $tw_1$
and
$tw_1$
and
![]() $w_2$
. Indeed, let
$w_2$
. Indeed, let
![]() $W(x,y)$
be a nontrivial reduced word of length
$W(x,y)$
be a nontrivial reduced word of length
![]() $k \lt n+1$
in the alphabet
$k \lt n+1$
in the alphabet
![]() $\{x^{\pm 1}, y^{\pm 1}\}$
such that
$\{x^{\pm 1}, y^{\pm 1}\}$
such that
![]() $W(tw_1,w_2) = 1\in B\wr A$
. For every
$W(tw_1,w_2) = 1\in B\wr A$
. For every
![]() $1\leq i\leq k$
, let also
$1\leq i\leq k$
, let also
![]() $W_i$
be the prefix of
$W_i$
be the prefix of
![]() $W$
of length
$W$
of length
![]() $i$
. Then
$i$
. Then
![]() $W(w_1,w_2) = W_k(w_1,w_2) = 1\in A$
, moreover, for at least one
$W(w_1,w_2) = W_k(w_1,w_2) = 1\in A$
, moreover, for at least one
![]() $i\in \{1,\ldots, k\}$
there exists
$i\in \{1,\ldots, k\}$
there exists
![]() $j\in \{1,\ldots, k\}\backslash \{i\}$
such that
$j\in \{1,\ldots, k\}\backslash \{i\}$
such that
![]() $W_i(w_1,w_2) = W_j(w_1, w_2)$
. Indeed, we have
$W_i(w_1,w_2) = W_j(w_1, w_2)$
. Indeed, we have
where
![]() $1\leq s\leq k, \epsilon _i\in \{-1,1\}, 1\leq i\leq s$
and
$1\leq s\leq k, \epsilon _i\in \{-1,1\}, 1\leq i\leq s$
and
![]() $0\leq n_1 \lt n_2 \lt \dots \lt n_s\leq k$
(here, we define
$0\leq n_1 \lt n_2 \lt \dots \lt n_s\leq k$
(here, we define
![]() $W_0 = 1$
).
$W_0 = 1$
).
Now, we have
![]() $W_{n_i}t^{\epsilon _i}W_{n_i}^{-1}\in \displaystyle \mathop{\bigoplus }_{\alpha \in A}B$
for all
$W_{n_i}t^{\epsilon _i}W_{n_i}^{-1}\in \displaystyle \mathop{\bigoplus }_{\alpha \in A}B$
for all
![]() $1\leq i\leq s$
. Moreover, by the re-indexing action of
$1\leq i\leq s$
. Moreover, by the re-indexing action of
![]() $A$
on
$A$
on
![]() $\displaystyle \mathop{\bigoplus }_{\alpha \in A}B$
, for each of the terms
$\displaystyle \mathop{\bigoplus }_{\alpha \in A}B$
, for each of the terms
![]() $W_{n_i}t^{\epsilon _i}W_{n_i}^{-1}$
we have only one nontrivial (i.e. non-identity) coordinate consisting of
$W_{n_i}t^{\epsilon _i}W_{n_i}^{-1}$
we have only one nontrivial (i.e. non-identity) coordinate consisting of
![]() $b$
or
$b$
or
![]() $b^{-1}$
depending if
$b^{-1}$
depending if
![]() $\epsilon _i = 1$
or
$\epsilon _i = 1$
or
![]() $\epsilon _i = -1$
respectively. Hence, to have a necessary cancelation, we need to have two distinct
$\epsilon _i = -1$
respectively. Hence, to have a necessary cancelation, we need to have two distinct
![]() $p,q\in \{1,\dots, s\}$
such that
$p,q\in \{1,\dots, s\}$
such that
![]() $W_{n_p} = W_{n_q}$
(and
$W_{n_p} = W_{n_q}$
(and
![]() $\epsilon _p = -\epsilon _q$
). Thus, we can take
$\epsilon _p = -\epsilon _q$
). Thus, we can take
![]() $i = n_p, j = n_q$
.
$i = n_p, j = n_q$
.
Thus, we established that for at least one
![]() $i\in \{1,\ldots, k\}$
there exists
$i\in \{1,\ldots, k\}$
there exists
![]() $j\in \{1,\ldots, k\}\backslash \{i\}$
such that
$j\in \{1,\ldots, k\}\backslash \{i\}$
such that
![]() $W_i(w_1,w_2) = W_j(w_1, w_2)$
. But this implies a relation of length less than
$W_i(w_1,w_2) = W_j(w_1, w_2)$
. But this implies a relation of length less than
![]() $n$
among
$n$
among
![]() $w_1$
and
$w_1$
and
![]() $w_2$
.
$w_2$
.
Let us note that in the proof of Lemma 3.1, we are using a careful re-examination of the word
![]() $W(tw_1, w_2)$
. We view the latter as a word in the alphabet
$W(tw_1, w_2)$
. We view the latter as a word in the alphabet
![]() $\{t^{\pm 1}, w_1^{\pm 1}, w_2^{\pm 1}\}$
. There will be no consecutive occurrences of
$\{t^{\pm 1}, w_1^{\pm 1}, w_2^{\pm 1}\}$
. There will be no consecutive occurrences of
![]() $t^{\pm 1}$
; as we read through from left to right, we write
$t^{\pm 1}$
; as we read through from left to right, we write
![]() $W(tw_1, w_2)$
as a product of conjugates of
$W(tw_1, w_2)$
as a product of conjugates of
![]() $t^{\pm 1}$
. The residue at the very right will be the word
$t^{\pm 1}$
. The residue at the very right will be the word
![]() $W(w_1, w_2)$
. For example, if
$W(w_1, w_2)$
. For example, if
![]() $W(x,y) = [x,y] = xyx^{-1}y^{-1}$
, then we will have
$W(x,y) = [x,y] = xyx^{-1}y^{-1}$
, then we will have
We also would like to observe the following simple lemma.
Lemma 3.2.
Let
![]() $T = [(f_1, \ldots, f_n, f_{n+1});\; (a_1,b_1), \ldots, (a_n, b_n), (a_{n+1}, b_{n+1})]$
be a suitable tower, and
$T = [(f_1, \ldots, f_n, f_{n+1});\; (a_1,b_1), \ldots, (a_n, b_n), (a_{n+1}, b_{n+1})]$
be a suitable tower, and
![]() $\phi _1, \ldots, \phi _n\in PL_o(I)$
be such that for all
$\phi _1, \ldots, \phi _n\in PL_o(I)$
be such that for all
![]() $i\in \{1, \ldots, n\}$
,
$i\in \{1, \ldots, n\}$
,
![]() $supp(\phi _i) \subseteq [a_i, b_i]$
and
$supp(\phi _i) \subseteq [a_i, b_i]$
and
![]() $\phi _i|_{[a_i,b_i]} = f_i|_{[a_i,b_i]}$
. Then
$\phi _i|_{[a_i,b_i]} = f_i|_{[a_i,b_i]}$
. Then
(a) the maps
![]() $\phi _1, \ldots, \phi _n$
generate a subgroup
$\phi _1, \ldots, \phi _n$
generate a subgroup
![]() $H_n\leq PL_o(I)$
such that there exists an isomorphism
$H_n\leq PL_o(I)$
such that there exists an isomorphism
![]() $\Phi : H_n\rightarrow G_n$
given by
$\Phi : H_n\rightarrow G_n$
given by
![]() $\Phi (\phi _i) = g_i, 1\leq i\leq n$
;
$\Phi (\phi _i) = g_i, 1\leq i\leq n$
;
(b) if
![]() $W = W(g_1, \ldots, g_n)$
is any non-identity element of
$W = W(g_1, \ldots, g_n)$
is any non-identity element of
![]() $G_n$
, then there exists a word
$G_n$
, then there exists a word
![]() $U = U(g_1, \ldots, g_n)\in G_n$
such that
$U = U(g_1, \ldots, g_n)\in G_n$
such that
![]() $W_1((U_1(a_{n+1}, b_{n+1})))\cap U_1((a_{n+1}, b_{n+1})) = \emptyset$
where
$W_1((U_1(a_{n+1}, b_{n+1})))\cap U_1((a_{n+1}, b_{n+1})) = \emptyset$
where
![]() $W_1 = W(\phi _1, \ldots, \phi _n), U_1 = U(\phi _1, \ldots, \phi _n)$
;
$W_1 = W(\phi _1, \ldots, \phi _n), U_1 = U(\phi _1, \ldots, \phi _n)$
;
(c) if
![]() $W = W(g_1, \ldots, g_n)\in G_n$
and
$W = W(g_1, \ldots, g_n)\in G_n$
and
![]() $x\in (a_{n+1}, b_{n+1})$
, then
$x\in (a_{n+1}, b_{n+1})$
, then
![]() $W(f_1, \ldots, f_n)(x) = W(\phi _1, \ldots, \phi _n)(x)$
.
$W(f_1, \ldots, f_n)(x) = W(\phi _1, \ldots, \phi _n)(x)$
.
Now, let
![]() $\Gamma$
be a finitely generated non-solvable subgroup of
$\Gamma$
be a finitely generated non-solvable subgroup of
![]() $PL_o(I)$
,
$PL_o(I)$
,
![]() $s = d(\Gamma )$
(i.e.
$s = d(\Gamma )$
(i.e.
![]() $s$
is the minimal cardinality for a generating subset of
$s$
is the minimal cardinality for a generating subset of
![]() $\Gamma$
). Without loss of generality, we may assume that
$\Gamma$
). Without loss of generality, we may assume that
![]() $\Gamma$
is irreducible, that is, it has no global fixed point in the interval
$\Gamma$
is irreducible, that is, it has no global fixed point in the interval
![]() $(0,1)$
.
$(0,1)$
.
For every finite generating set
![]() $X$
of
$X$
of
![]() $\Gamma$
, we will fix the left-invariant Cayley metric on
$\Gamma$
, we will fix the left-invariant Cayley metric on
![]() $\Gamma$
with respect to
$\Gamma$
with respect to
![]() $X$
, and let
$X$
, and let
![]() $B_k(1;\; X)$
denote the ball of radius
$B_k(1;\; X)$
denote the ball of radius
![]() $k$
centered at identity element
$k$
centered at identity element
![]() $1\in \Gamma$
, for all
$1\in \Gamma$
, for all
![]() $k\geq 1$
. We also let
$k\geq 1$
. We also let
Fix a positive integer
![]() $m$
, and let
$m$
, and let
![]() $q = 2m^2$
. By Lemma 3.1, there exists
$q = 2m^2$
. By Lemma 3.1, there exists
![]() $r\in \mathbb{N}$
such that in the group
$r\in \mathbb{N}$
such that in the group
![]() $G_r$
there exist
$G_r$
there exist
![]() $s$
elements
$s$
elements
![]() $w_1, w_2, \ldots, w_s$
such that there is no relation of length less than
$w_1, w_2, \ldots, w_s$
such that there is no relation of length less than
![]() $q$
among
$q$
among
![]() $w_1, \ldots, w_s$
. Let
$w_1, \ldots, w_s$
. Let
![]() $g_1, \ldots, g_r$
be the standard generators of
$g_1, \ldots, g_r$
be the standard generators of
![]() $G_r$
and let
$G_r$
and let
![]() $w_i = W_i(g_1, \ldots, g_r)$
,
$w_i = W_i(g_1, \ldots, g_r)$
,
![]() $1\leq i\leq s$
, where
$1\leq i\leq s$
, where
![]() $W_i$
is a reduced word in the free group of rank
$W_i$
is a reduced word in the free group of rank
![]() $r$
formally generated by the letters
$r$
formally generated by the letters
![]() $g_1, \ldots, g_r$
.
$g_1, \ldots, g_r$
.
Since
![]() $\Gamma$
is non-solvable, the commutator subgroup
$\Gamma$
is non-solvable, the commutator subgroup
![]() $[\Gamma, \Gamma ]$
is non-solvable. Then by Remark 2.3 and Lemma 2.11, there exists an ordered
$[\Gamma, \Gamma ]$
is non-solvable. Then by Remark 2.3 and Lemma 2.11, there exists an ordered
![]() $(r+1)$
-tuple
$(r+1)$
-tuple
![]() $(f_1, \ldots, f_r, f_{r+1})$
of elements of
$(f_1, \ldots, f_r, f_{r+1})$
of elements of
![]() $[\Gamma, \Gamma ]$
which form a suitable tower of height
$[\Gamma, \Gamma ]$
which form a suitable tower of height
![]() $r+1$
. Let
$r+1$
. Let
![]() $0 \lt d \lt D \lt 1$
such that
$0 \lt d \lt D \lt 1$
such that
![]() $\displaystyle \mathop{\cup }_{1\leq i\leq r+1}supp(f_i)\subset (d,D)$
.
$\displaystyle \mathop{\cup }_{1\leq i\leq r+1}supp(f_i)\subset (d,D)$
.
Then, we can find
![]() $\epsilon _0 \gt 0$
, a finite generating set
$\epsilon _0 \gt 0$
, a finite generating set
![]() $S$
of
$S$
of
![]() $\Gamma$
of cardinality
$\Gamma$
of cardinality
![]() $s$
, and a suitable tower
$s$
, and a suitable tower
![]() $(h_1, \ldots, h_{r}, h_{r+1})$
of elements of
$(h_1, \ldots, h_{r}, h_{r+1})$
of elements of
![]() $\Gamma$
with bases
$\Gamma$
with bases
![]() $(a_i, b_i)\subset (0, \epsilon _0), 1\leq i\leq r+1$
and
$(a_i, b_i)\subset (0, \epsilon _0), 1\leq i\leq r+1$
and
![]() $\Omega = \displaystyle \mathop{\cup }_{1\leq i\leq r+1}supp(h_i)$
such that
$\Omega = \displaystyle \mathop{\cup }_{1\leq i\leq r+1}supp(h_i)$
such that
![]() $S\cap S^{-1} = \emptyset$
and the following conditions hold:
$S\cap S^{-1} = \emptyset$
and the following conditions hold:
-
(i) for all
 $\beta \in B_{2m}(1;\; S), \beta (\Omega )\subset (0, \epsilon _0)$
;
$\beta \in B_{2m}(1;\; S), \beta (\Omega )\subset (0, \epsilon _0)$
; -
(ii) for any two distinct
 $c_1, c_2 \in \mathbb{R}_{+}$
, and for all
$c_1, c_2 \in \mathbb{R}_{+}$
, and for all
 $\beta _1\in S_{2m}(\Gamma, S, c_1), \beta _2\in S_{2m}(\Gamma, S, c_2)$
,
$\beta _1\in S_{2m}(\Gamma, S, c_1), \beta _2\in S_{2m}(\Gamma, S, c_2)$
,
 $\beta _1(\Omega )\cap \beta _2(\Omega ) = \emptyset$
;
$\beta _1(\Omega )\cap \beta _2(\Omega ) = \emptyset$
; -
(iii) for all
 $c\in \mathbb{R}_{+}, \beta _1, \beta _2\in S_{2m}(\Gamma, S, c)$
, and for all
$c\in \mathbb{R}_{+}, \beta _1, \beta _2\in S_{2m}(\Gamma, S, c)$
, and for all
 $x\in \Omega$
,
$x\in \Omega$
,
 $\beta _1(x) = \beta _2(x)$
(so, in particular, for all
$\beta _1(x) = \beta _2(x)$
(so, in particular, for all
 $\beta \in S_{2m}(\Gamma, S)$
and for all
$\beta \in S_{2m}(\Gamma, S)$
and for all
 $x\in \Omega, \ \beta (x) = x$
).
$x\in \Omega, \ \beta (x) = x$
).
Indeed, let
![]() $X_0 = \{\alpha _1, \dots, \alpha _s\}$
be any generating set of
$X_0 = \{\alpha _1, \dots, \alpha _s\}$
be any generating set of
![]() $\Gamma$
of cardinality
$\Gamma$
of cardinality
![]() $s$
. Without loss of generality, we may assume that
$s$
. Without loss of generality, we may assume that
Let
![]() $\delta \gt 0$
such that
$\delta \gt 0$
such that
![]() $\alpha _s$
has no singularity in
$\alpha _s$
has no singularity in
![]() $(0,\delta )$
. By irreducibility, there exists
$(0,\delta )$
. By irreducibility, there exists
![]() $\phi \in \Gamma$
such that
$\phi \in \Gamma$
such that
![]() $\phi (D) \lt \delta$
. For
$\phi (D) \lt \delta$
. For
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $1\leq i\leq r+1$
, we let
$1\leq i\leq r+1$
, we let
![]() $f_i^{(n)} = \psi _n^{-1} f_i\psi _n$
, where
$f_i^{(n)} = \psi _n^{-1} f_i\psi _n$
, where
![]() $\psi _n = \phi ^{-1}\alpha _s^n$
. Let also
$\psi _n = \phi ^{-1}\alpha _s^n$
. Let also
![]() $(d_n, D_n) = \psi _n^{-1}((d,D)), n\geq 1$
. Notice that the interval
$(d_n, D_n) = \psi _n^{-1}((d,D)), n\geq 1$
. Notice that the interval
![]() $(d_n, D_n)$
(in particular, its subset
$(d_n, D_n)$
(in particular, its subset
![]() $ \mathop{\cup }_{1\leq i\leq r+1}supp(f_i^{(n)})$
) converges to zero as
$ \mathop{\cup }_{1\leq i\leq r+1}supp(f_i^{(n)})$
) converges to zero as
![]() $n\to \infty$
; moreover, there exists a positive integer
$n\to \infty$
; moreover, there exists a positive integer
![]() $p$
such that for all
$p$
such that for all
![]() $k\geq p$
, we have
$k\geq p$
, we have
![]() $\frac{D_k}{d_k} = \frac{D_p}{d_p}$
.
$\frac{D_k}{d_k} = \frac{D_p}{d_p}$
.
We can choose a finite generating set
![]() $S = \{\gamma _1, \dots, \gamma _s\}$
such that the inequality
$S = \{\gamma _1, \dots, \gamma _s\}$
such that the inequality
![]() $\min \{c\in C_{2m}(\Gamma, S) \ | \ c \gt 1\} \gt \frac{D_p}{d_p}$
holds. To see this, first, we let
$\min \{c\in C_{2m}(\Gamma, S) \ | \ c \gt 1\} \gt \frac{D_p}{d_p}$
holds. To see this, first, we let
![]() $X_1 = \{\beta _1, \dots, \beta _s\}$
where
$X_1 = \{\beta _1, \dots, \beta _s\}$
where
![]() $\beta _s = \alpha _s$
, and
$\beta _s = \alpha _s$
, and
![]() $\beta _i = \alpha _i\alpha _{s}^{n_i}, 1\leq i\leq s-1$
for some
$\beta _i = \alpha _i\alpha _{s}^{n_i}, 1\leq i\leq s-1$
for some
![]() $n_{s-1}\leq \dots \leq n_2\leq n_1$
such that
$n_{s-1}\leq \dots \leq n_2\leq n_1$
such that
![]() $1 \lt \beta^{\prime}_s(0) \leq \beta^{\prime}_{s-1}(0) \leq \dots \leq \beta _1'(0)$
and
$1 \lt \beta^{\prime}_s(0) \leq \beta^{\prime}_{s-1}(0) \leq \dots \leq \beta _1'(0)$
and
![]() $\beta _{1}'(0) \gt \frac{D_p}{d_p}$
. After this, we modify the generating set
$\beta _{1}'(0) \gt \frac{D_p}{d_p}$
. After this, we modify the generating set
![]() $X_1$
further by letting
$X_1$
further by letting
![]() $S = \{\beta _1, \beta _1^{\lambda }\beta _2, \beta _1^{\lambda ^2}\beta _{3}, \dots, \beta _1^{\lambda ^{s-1}}\beta _{s}\}$
where
$S = \{\beta _1, \beta _1^{\lambda }\beta _2, \beta _1^{\lambda ^2}\beta _{3}, \dots, \beta _1^{\lambda ^{s-1}}\beta _{s}\}$
where
![]() $\lambda = 4m+1$
.
$\lambda = 4m+1$
.
Then, for sufficiently big
![]() $n$
, we can take
$n$
, we can take
![]() $h_i = f_i^{(n)}, 1\leq i\leq r+1$
to satisfy the claims (i)–(iii).
$h_i = f_i^{(n)}, 1\leq i\leq r+1$
to satisfy the claims (i)–(iii).
Now, let
![]() $A_m$
be a minimal subset of
$A_m$
be a minimal subset of
![]() $B_m(1;S)$
such that
$B_m(1;S)$
such that
![]() $A_m\cap S_m(\Gamma, S, c) \neq \emptyset$
for every
$A_m\cap S_m(\Gamma, S, c) \neq \emptyset$
for every
![]() $c\in C_m(\Gamma, S)$
; and for all
$c\in C_m(\Gamma, S)$
; and for all
![]() $k\in \{1, \ldots, s\}$
, let
$k\in \{1, \ldots, s\}$
, let
where
![]() $v_k = W_k(h_1, \ldots, h_r), u_k = v_k^m$
and for the products (the formulas for
$v_k = W_k(h_1, \ldots, h_r), u_k = v_k^m$
and for the products (the formulas for
![]() $\omega _k$
and
$\omega _k$
and
![]() $\eta _k$
) we choose any linear order on the set
$\eta _k$
) we choose any linear order on the set
![]() $A_m$
.
$A_m$
.
Notice that because of conditions (i)–(iii), for any two
![]() $\gamma ', \gamma ''\in B_m(1)$
, we have
$\gamma ', \gamma ''\in B_m(1)$
, we have
![]() $[\gamma 'v_k(\gamma ')^{-1}, \gamma ''v_k(\gamma '')^{-1}] = 1$
and
$[\gamma 'v_k(\gamma ')^{-1}, \gamma ''v_k(\gamma '')^{-1}] = 1$
and
![]() $[\gamma 'u_k(\gamma ')^{-1}, \gamma ''u_k(\gamma '')^{-1}] = 1$
, so the order in the products
$[\gamma 'u_k(\gamma ')^{-1}, \gamma ''u_k(\gamma '')^{-1}] = 1$
, so the order in the products
![]() $\displaystyle \prod _{\gamma \in A_m}(\gamma v_k\gamma ^{-1})$
and
$\displaystyle \prod _{\gamma \in A_m}(\gamma v_k\gamma ^{-1})$
and
![]() $\displaystyle \prod _{\gamma \in A_m}(\gamma u_k\gamma ^{-1})$
does not matter.
$\displaystyle \prod _{\gamma \in A_m}(\gamma u_k\gamma ^{-1})$
does not matter.
Now, let
![]() $S^{(m)} = \{\eta _1\gamma _1\eta _2, \eta _2\gamma _2 \eta _3, \ldots, \eta _s\gamma _s\eta _1, \omega _1, \ldots, \omega _s\}$
. Then, since
$S^{(m)} = \{\eta _1\gamma _1\eta _2, \eta _2\gamma _2 \eta _3, \ldots, \eta _s\gamma _s\eta _1, \omega _1, \ldots, \omega _s\}$
. Then, since
![]() $\omega _k^m = \eta _k$
for all
$\omega _k^m = \eta _k$
for all
![]() $1\leq k\leq s$
, the set
$1\leq k\leq s$
, the set
![]() $S^{(m)}$
generates
$S^{(m)}$
generates
![]() $\Gamma$
, and there is no relation of length less than
$\Gamma$
, and there is no relation of length less than
![]() $m$
among the elements of
$m$
among the elements of
![]() $S^{(m)}$
.
$S^{(m)}$
.
Indeed, let
![]() $R = R(\eta _1\gamma _1\eta _2, \eta _2\gamma _2 \eta _3, \ldots, \eta _s\gamma _s\eta _1, \omega _1, \ldots, \omega _s)$
denote such a relation. Then, we can write
$R = R(\eta _1\gamma _1\eta _2, \eta _2\gamma _2 \eta _3, \ldots, \eta _s\gamma _s\eta _1, \omega _1, \ldots, \omega _s)$
denote such a relation. Then, we can write
where
![]() $n\leq m$
,
$n\leq m$
,
![]() $\theta _i\in B_m(1)$
for all
$\theta _i\in B_m(1)$
for all
![]() $1\leq i\leq n$
, and
$1\leq i\leq n$
, and
![]() $R_j = R_j(\eta _1, \ldots, \eta _s, \omega _1, \ldots, \omega _s)$
is a reduced word of length at most
$R_j = R_j(\eta _1, \ldots, \eta _s, \omega _1, \ldots, \omega _s)$
is a reduced word of length at most
![]() $m$
for all
$m$
for all
![]() $0\leq j\leq n+1$
; moreover,
$0\leq j\leq n+1$
; moreover,
![]() $R_1, \ldots, R_n$
are nontrivial.
$R_1, \ldots, R_n$
are nontrivial.
Notice that for all
![]() $g\in B_m(1;\; S)$
, the shift
$g\in B_m(1;\; S)$
, the shift
![]() $gB_m(1;\; S)$
still contains
$gB_m(1;\; S)$
still contains
![]() $1\in \Gamma$
. Then we obtain a nontrivial relation
$1\in \Gamma$
. Then we obtain a nontrivial relation
![]() $V(v_1, \ldots, v_s)$
among
$V(v_1, \ldots, v_s)$
among
![]() $v_1, \ldots, v_s$
of length at most
$v_1, \ldots, v_s$
of length at most
![]() $2m^2$
.Footnote 2 We can write
$2m^2$
.Footnote 2 We can write
![]() $V(v_1, \ldots, v_s) = W(h_1, \ldots, h_r) = 1$
where
$V(v_1, \ldots, v_s) = W(h_1, \ldots, h_r) = 1$
where
![]() $W$
is a nontrivial reduced word. Notice that
$W$
is a nontrivial reduced word. Notice that
![]() $V(v_1, \ldots, v_s) = W(h_1, \ldots, h_r)$
represents a map in
$V(v_1, \ldots, v_s) = W(h_1, \ldots, h_r)$
represents a map in
![]() $PL_o(I)$
, while
$PL_o(I)$
, while
![]() $V(w_1,\ldots, w_s)$
represents a word in
$V(w_1,\ldots, w_s)$
represents a word in
![]() $G_r$
which by our choices does not represent an identity element in
$G_r$
which by our choices does not represent an identity element in
![]() $G_r$
. Then, by Lemma 3.2, for some word
$G_r$
. Then, by Lemma 3.2, for some word
![]() $U = U(h_1, \ldots, h_r)$
and for all
$U = U(h_1, \ldots, h_r)$
and for all
![]() $x\in U((a_{r+1}, b_{r+1}))$
we have
$x\in U((a_{r+1}, b_{r+1}))$
we have
![]() $W(x)\notin U((a_{r+1}, b_{r+1}))$
, thus
$W(x)\notin U((a_{r+1}, b_{r+1}))$
, thus
![]() $W(x)\neq x$
. Since
$W(x)\neq x$
. Since
![]() $m$
is arbitrary, we conclude that
$m$
is arbitrary, we conclude that
![]() $girth(\Gamma ) = \infty$
.
$girth(\Gamma ) = \infty$
.
The main idea of the proof of Theorem 1.2 is described below. For any given
![]() $q, k$
, in a suitable tower of sufficiently big height
$q, k$
, in a suitable tower of sufficiently big height
![]() $r$
, formed by PL-maps
$r$
, formed by PL-maps
![]() $\phi _1, \ldots, \phi _r, \phi _{r+1}$
, one can find words
$\phi _1, \ldots, \phi _r, \phi _{r+1}$
, one can find words
![]() $w_1, \ldots, w_k$
in the alphabet
$w_1, \ldots, w_k$
in the alphabet
![]() $\{\phi _1^{\pm 1}, \ldots, \phi _r^{\pm 1}\}$
such that the corresponding elements (let us denote them by
$\{\phi _1^{\pm 1}, \ldots, \phi _r^{\pm 1}\}$
such that the corresponding elements (let us denote them by
![]() $\overline{w_1}, \ldots, \overline{w_k}$
) do not have a relation of length less than
$\overline{w_1}, \ldots, \overline{w_k}$
) do not have a relation of length less than
![]() $q$
. This is because, upon the action on the innermost base of the tower (an orbital of
$q$
. This is because, upon the action on the innermost base of the tower (an orbital of
![]() $\phi _{r+1}$
), a suitable tower behaves as if the maps generate a genuine copy of
$\phi _{r+1}$
), a suitable tower behaves as if the maps generate a genuine copy of
![]() $G_r$
, for elements in the ball of certain radius. The problem is how to find a finite generating set without a short relation among the generators, not just among some elements. For this, we pick up a tower with sufficient height such that the PL homeomorphisms forming this tower are supported in a very small interval. This interval can be made arbitrarily small; therefore, using irreducibility of
$G_r$
, for elements in the ball of certain radius. The problem is how to find a finite generating set without a short relation among the generators, not just among some elements. For this, we pick up a tower with sufficient height such that the PL homeomorphisms forming this tower are supported in a very small interval. This interval can be made arbitrarily small; therefore, using irreducibility of
![]() $\Gamma$
, one can push this support (interval) close enough to the end 0 of the interval
$\Gamma$
, one can push this support (interval) close enough to the end 0 of the interval
![]() $[0,1]$
such that the new support
$[0,1]$
such that the new support
![]() $\Omega$
satisfies conditions (i)–(iii), namely, (i) any PL map
$\Omega$
satisfies conditions (i)–(iii), namely, (i) any PL map
![]() $\beta$
from the ball
$\beta$
from the ball
![]() $B_m(1)$
still keeps
$B_m(1)$
still keeps
![]() $\Omega$
inside an interval
$\Omega$
inside an interval
![]() $(0,\epsilon _0)$
; (ii) the image of
$(0,\epsilon _0)$
; (ii) the image of
![]() $\Omega$
by elements of
$\Omega$
by elements of
![]() $B_m(1)$
with different slopes at 0 are disjoint; and (iii) the images of
$B_m(1)$
with different slopes at 0 are disjoint; and (iii) the images of
![]() $\Omega$
by elements of
$\Omega$
by elements of
![]() $B_m(1)$
with the same slope at 0 are the same. Then we pick up a generating set which involves the elements
$B_m(1)$
with the same slope at 0 are the same. Then we pick up a generating set which involves the elements
![]() $\overline{w_1}, \ldots, \overline{w_k}$
. By properties (i)–(iii), we again obtain a short relation among
$\overline{w_1}, \ldots, \overline{w_k}$
. By properties (i)–(iii), we again obtain a short relation among
![]() $\overline{w_1}, \ldots, \overline{w_k}$
thus a contradiction.
$\overline{w_1}, \ldots, \overline{w_k}$
thus a contradiction.
4. Girth of subgroups with hyperbolic-like elements
In this section, we will prove Theorem 1.5.
Let
![]() $d(\Gamma ) = s$
, and
$d(\Gamma ) = s$
, and
![]() $m$
be a natural number. We will find
$m$
be a natural number. We will find
![]() $s+2$
generators of
$s+2$
generators of
![]() $\Gamma$
such that there is no relation of length
$\Gamma$
such that there is no relation of length
![]() $m$
or less in
$m$
or less in
![]() $\Gamma$
in these generators. (since
$\Gamma$
in these generators. (since
![]() $m$
is arbitrary, this proves that
$m$
is arbitrary, this proves that
![]() $girth(\Gamma ) = \infty$
).
$girth(\Gamma ) = \infty$
).
Let
![]() $S = \{X_1, \ldots, X_s\}$
be a finite generating set of
$S = \{X_1, \ldots, X_s\}$
be a finite generating set of
![]() $\Gamma$
, and
$\Gamma$
, and
![]() $S^{\ast }$
be the symmetrization of
$S^{\ast }$
be the symmetrization of
![]() $S$
, that is
$S$
, that is
![]() $S^{\ast } = \{X_1, \ldots, X_s, X_1^{-1}, \ldots, X_s^{-1}\}$
. Let also
$S^{\ast } = \{X_1, \ldots, X_s, X_1^{-1}, \ldots, X_s^{-1}\}$
. Let also
![]() $p_0\in (0,1)$
(one could take
$p_0\in (0,1)$
(one could take
![]() $p_0 = \frac{1}{2}$
). We can find a natural number
$p_0 = \frac{1}{2}$
). We can find a natural number
![]() $N \gt 4m$
and a sequence
$N \gt 4m$
and a sequence
![]() $0 = c_0 \lt c_1 \lt c_2 \lt \ldots \lt c_{2N} \lt c_{2N+1} = 1$
such that the following three conditions are satisfied.
$0 = c_0 \lt c_1 \lt c_2 \lt \ldots \lt c_{2N} \lt c_{2N+1} = 1$
such that the following three conditions are satisfied.
-
(i)
 $p_0\in (c_{N}, c_{N+1})$
;
$p_0\in (c_{N}, c_{N+1})$
; -
(ii) for all
 $X\in S^{\ast }$
and
$X\in S^{\ast }$
and
 $p\in \{p_0, c_1, \dots, c_{2N}\}, X(p)\notin \{c_1, \ldots, c_{2N}\}\backslash \{p\}$
;
$p\in \{p_0, c_1, \dots, c_{2N}\}, X(p)\notin \{c_1, \ldots, c_{2N}\}\backslash \{p\}$
; -
(iii)
 $W(X_1, \ldots, X_s, Y_N)(p_0)\subset (c_1, c_{2N})$
for all reduced words
$W(X_1, \ldots, X_s, Y_N)(p_0)\subset (c_1, c_{2N})$
for all reduced words
 $W$
of the form
$W$
of the form
 $W_0Y_N^{n_1}W_1Y_N^{n_2}\ldots W_{k-1} Y_N^{n_k}W_k$
where
$W_0Y_N^{n_1}W_1Y_N^{n_2}\ldots W_{k-1} Y_N^{n_k}W_k$
where
 $Y_N$
is any orientation-preserving homeomorphism satisfying the conditions
$Y_N$
is any orientation-preserving homeomorphism satisfying the conditions
 $Y_N(c_i) = c_{i+4}, 1\leq i\leq 2N-4$
,
$Y_N(c_i) = c_{i+4}, 1\leq i\leq 2N-4$
,
 $n_1, \ldots, n_k\in \{-1, 1\}$
, and
$n_1, \ldots, n_k\in \{-1, 1\}$
, and
 $W_i$
is a reduced word in the alphabet
$W_i$
is a reduced word in the alphabet
 $\{X_1^{\pm 1}, \ldots, X_s^{\pm 1}\}$
of length
$\{X_1^{\pm 1}, \ldots, X_s^{\pm 1}\}$
of length
 $L_i, 0\leq i\leq k$
where
$L_i, 0\leq i\leq k$
where
 $\displaystyle \sum _{i=0}^kL_i \leq 2m$
.
$\displaystyle \sum _{i=0}^kL_i \leq 2m$
.
Notice that condition (iii) implies that
where
![]() $d = 2m - \displaystyle \mathop{\sum }_{i=0}^{k}L_i$
.
$d = 2m - \displaystyle \mathop{\sum }_{i=0}^{k}L_i$
.
Let
![]() $\delta = \displaystyle \min _{0\leq i\leq 2N} |c_{i+1}-c_i|$
and
$\delta = \displaystyle \min _{0\leq i\leq 2N} |c_{i+1}-c_i|$
and
![]() $\epsilon \lt \frac{1}{8}\min \{\delta, |p_0-c_N|, |p_0-c_{N+1}|\}$
be such that
$\epsilon \lt \frac{1}{8}\min \{\delta, |p_0-c_N|, |p_0-c_{N+1}|\}$
be such that
![]() $X(p-\epsilon, p+\epsilon )\cap (q-\epsilon, q+\epsilon ) = \emptyset$
for all
$X(p-\epsilon, p+\epsilon )\cap (q-\epsilon, q+\epsilon ) = \emptyset$
for all
![]() $X\in S^{\ast }$
and distinct
$X\in S^{\ast }$
and distinct
![]() $p, q\in \{p_0, c_1, \dots, c_{2N}\}$
. Then we can find a natural number
$p, q\in \{p_0, c_1, \dots, c_{2N}\}$
. Then we can find a natural number
![]() $M \gt 2m$
and elements
$M \gt 2m$
and elements
![]() $\gamma, \theta \in \Gamma$
such that:
$\gamma, \theta \in \Gamma$
such that:
-
(iv)
 $Fix(\gamma ) = \{0, a_1, a_2, \ldots, a_N, 1\}, Fix(\theta ) = \{0, b_1, b_2, \ldots, b_N, 1\}$
and for all
$Fix(\gamma ) = \{0, a_1, a_2, \ldots, a_N, 1\}, Fix(\theta ) = \{0, b_1, b_2, \ldots, b_N, 1\}$
and for all
 $1\leq i\leq N$
, the inequalities
$1\leq i\leq N$
, the inequalities
 $|a_i-c_{2i-1}| \lt \epsilon$
and
$|a_i-c_{2i-1}| \lt \epsilon$
and
 $|b_i-c_{2i}| \lt \epsilon$
hold;
$|b_i-c_{2i}| \lt \epsilon$
hold; -
(v) for all
 $n\geq M$
, we have
$n\geq M$
, we have
 $\gamma ^{\pm n}(U_{\gamma })\subset V_{\gamma }$
where
$\gamma ^{\pm n}(U_{\gamma })\subset V_{\gamma }$
where \begin{align*}U_{\gamma } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N}(a_i + \epsilon, a_{i+1} - \epsilon ), V_{\gamma } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N+1}(a_i - \epsilon, a_i + \epsilon );\end{align*}
\begin{align*}U_{\gamma } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N}(a_i + \epsilon, a_{i+1} - \epsilon ), V_{\gamma } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N+1}(a_i - \epsilon, a_i + \epsilon );\end{align*}
-
(vi) for all
 $n\geq M$
, we have
$n\geq M$
, we have
 $\theta ^{\pm n}(U_{\theta })\subset V_{\theta }$
where
$\theta ^{\pm n}(U_{\theta })\subset V_{\theta }$
where \begin{align*}U_{\theta } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N}(b_i + \epsilon, b_{i+1} - \epsilon ), V_{\theta } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N+1}(b_i - \epsilon, b_i + \epsilon ).\end{align*}
\begin{align*}U_{\theta } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N}(b_i + \epsilon, b_{i+1} - \epsilon ), V_{\theta } = \displaystyle \mathop {\sqcup } _{0\leq i\leq N+1}(b_i - \epsilon, b_i + \epsilon ).\end{align*}
It is straightforward to make all these arrangements. (Let us also clarify that we define
![]() $a_0 = b_0 = 0$
and
$a_0 = b_0 = 0$
and
![]() $a_{N+1} = b_{N+1} = 1$
.)
$a_{N+1} = b_{N+1} = 1$
.)
Notice that
![]() $p_0\in U_{\gamma } \cup U_{\theta }$
and
$p_0\in U_{\gamma } \cup U_{\theta }$
and
![]() $p_0\notin V_{\gamma } \cup V_{\theta }$
. Now, let
$p_0\notin V_{\gamma } \cup V_{\theta }$
. Now, let
![]() $r \geq 2M$
, and
$r \geq 2M$
, and
![]() $S' = \{\gamma ^r, \theta ^r, \gamma ^{r^2}X_1\theta ^{r^2}, \ldots, \gamma ^{sr^2}X_s\theta ^{sr^2} \}$
.
$S' = \{\gamma ^r, \theta ^r, \gamma ^{r^2}X_1\theta ^{r^2}, \ldots, \gamma ^{sr^2}X_s\theta ^{sr^2} \}$
.
Then if
![]() $W_0$
is a nontrivial reduced word in these generators of length at most
$W_0$
is a nontrivial reduced word in these generators of length at most
![]() $m$
, and if
$m$
, and if
![]() $W'$
is any suffix of
$W'$
is any suffix of
![]() $W_0$
in the alphabet
$W_0$
in the alphabet
![]() $S'$
, then because of (i)–(vi), we have
$S'$
, then because of (i)–(vi), we have
![]() $W'(p_0)\in (c_1, c_N)$
.
$W'(p_0)\in (c_1, c_N)$
.
Indeed,
![]() $W'$
can be written as:
$W'$
can be written as:
where for all
![]() $1\leq i\leq k$
,
$1\leq i\leq k$
,
![]() $j_i\in \{1,\dots,s\}, \epsilon _i\in \{-1,1\}$
and
$j_i\in \{1,\dots,s\}, \epsilon _i\in \{-1,1\}$
and
![]() $\alpha _i, 1\leq i\leq k+1$
belong to the set:
$\alpha _i, 1\leq i\leq k+1$
belong to the set:
From the re-writing
![]() $W'$
as a suffix of
$W'$
as a suffix of
![]() $W_0$
, we obtain that
$W_0$
, we obtain that
![]() $k\leq m$
. On the other hand, for all
$k\leq m$
. On the other hand, for all
![]() $1\leq i\leq k, \epsilon \in \{-1,1\}$
and
$1\leq i\leq k, \epsilon \in \{-1,1\}$
and
![]() $x\in (c_4, c_{N-4})$
we have the inequality
$x\in (c_4, c_{N-4})$
we have the inequality
![]() $Y_N^{-1}(x) \lt \alpha _i^{\epsilon }(x) \lt Y_N(x)$
. Then letting
$Y_N^{-1}(x) \lt \alpha _i^{\epsilon }(x) \lt Y_N(x)$
. Then letting
![]() $W_i = X_{n_i}^{\epsilon _i}, 1\leq i\leq k$
, we obtain that
$W_i = X_{n_i}^{\epsilon _i}, 1\leq i\leq k$
, we obtain that
![]() $|W_i|= 1, 1\leq i\leq k$
in the alphabet
$|W_i|= 1, 1\leq i\leq k$
in the alphabet
![]() $S^{\ast }$
, hence
$S^{\ast }$
, hence
![]() $ \displaystyle \mathop{\sum }_{i=1}^{k}|W_i| = k \leq m \lt \frac{N}{4}$
.
$ \displaystyle \mathop{\sum }_{i=1}^{k}|W_i| = k \leq m \lt \frac{N}{4}$
.
By condition (iii), for every suffix
![]() $W''$
of
$W''$
of
![]() $W'$
, we have
$W'$
, we have
![]() $W''(p_0)\in (c_1, c_{2N})$
, in fact,
$W''(p_0)\in (c_1, c_{2N})$
, in fact,
![]() $W''(p_0)\in (c_{1+4d}, c_{2N-4d})$
where
$W''(p_0)\in (c_{1+4d}, c_{2N-4d})$
where
![]() $d = 2m-L$
and
$d = 2m-L$
and
![]() $L$
is the number of occurrences of
$L$
is the number of occurrences of
![]() $X_i^{\pm 1}, 1\leq i\leq s$
in
$X_i^{\pm 1}, 1\leq i\leq s$
in
![]() $W''$
. So, we have
$W''$
. So, we have
![]() $W'(p_0)\in (c_{1+4d}, c_{2N-4d})$
with
$W'(p_0)\in (c_{1+4d}, c_{2N-4d})$
with
![]() $d = 2m-k$
.
$d = 2m-k$
.
Then, inductively (ping-pong argument),
![]() $W_0(p_0)\in V_{\gamma }\cup V_{\theta }$
; more precisely,
$W_0(p_0)\in V_{\gamma }\cup V_{\theta }$
; more precisely,
![]() $W_0(p_0)\in V_{\gamma }$
if
$W_0(p_0)\in V_{\gamma }$
if
![]() $W_0$
starts with
$W_0$
starts with
![]() $\gamma ^{\pm 1}$
and
$\gamma ^{\pm 1}$
and
![]() $W_0(p_0)\in V_{\theta }$
if
$W_0(p_0)\in V_{\theta }$
if
![]() $W_0$
starts with
$W_0$
starts with
![]() $\theta ^{\pm 1}$
. Then,
$\theta ^{\pm 1}$
. Then,
![]() $W_0(p_0)\neq p_0$
, hence
$W_0(p_0)\neq p_0$
, hence
![]() $W_0\neq 1$
.
$W_0\neq 1$
.
Remark 4.1. The assumptions of Theorem 1.5 can be weakened significantly (at the expense of making the statement more technical).
The proof of Theorem 1.5 uses the well-known “ping-pong idea” where one designs a certain “ping-pong table” which could involve two or more sets (in our case
![]() $U_{\gamma }$
and
$U_{\gamma }$
and
![]() $U_{\theta }$
), and (in one of the versions) the point (in our case
$U_{\theta }$
), and (in one of the versions) the point (in our case
![]() $p_0$
) taken outside of these sets arrives to one of these sets and then either jumps from one to another never returning back to its original position or in a slightly more subtle version as in our case, even if it leaves
$p_0$
) taken outside of these sets arrives to one of these sets and then either jumps from one to another never returning back to its original position or in a slightly more subtle version as in our case, even if it leaves
![]() $U_{\gamma }\cup U_{\theta }$
(in our case this might happen by the action of
$U_{\gamma }\cup U_{\theta }$
(in our case this might happen by the action of
![]() $X\in S^{\ast }$
), then immediately returns back to it. In condition (i) of our proof,
$X\in S^{\ast }$
), then immediately returns back to it. In condition (i) of our proof,
![]() $p_0$
is taken in the middle interval just for convenience. We are following the orbit of it by the consecutive suffixes of
$p_0$
is taken in the middle interval just for convenience. We are following the orbit of it by the consecutive suffixes of
![]() $W_0$
. Notice that by our choice of
$W_0$
. Notice that by our choice of
![]() $r$
, there will not be any occurrence of
$r$
, there will not be any occurrence of
![]() $X_i^{\pm 1}X_j^{\pm 1}$
in
$X_i^{\pm 1}X_j^{\pm 1}$
in
![]() $W_0$
; moreover, the exponents of both
$W_0$
; moreover, the exponents of both
![]() $\gamma$
and
$\gamma$
and
![]() $\theta$
are sufficiently big. By condition (ii) and the choice of
$\theta$
are sufficiently big. By condition (ii) and the choice of
![]() $\epsilon$
, our point stays away from
$\epsilon$
, our point stays away from
![]() $Fix (\gamma )\cup Fix(\theta )$
whenever
$Fix (\gamma )\cup Fix(\theta )$
whenever
![]() $X\in S^{\ast }$
is applied. It may get close to
$X\in S^{\ast }$
is applied. It may get close to
![]() $Fix (\gamma )$
, then hits
$Fix (\gamma )$
, then hits
![]() $U_{\gamma }$
and is immediately taken away from it by
$U_{\gamma }$
and is immediately taken away from it by
![]() $X\in S^{\ast }$
or by sufficiently big powers of
$X\in S^{\ast }$
or by sufficiently big powers of
![]() $\theta$
. Similar effect happens when we get close to
$\theta$
. Similar effect happens when we get close to
![]() $Fix(\theta )$
. Condition (iii) guarantees that we stay in the field of action where arrangements are suitable.
$Fix(\theta )$
. Condition (iii) guarantees that we stay in the field of action where arrangements are suitable.
Remark 4.2.
From the proof we see that one can state a much more general theorem for the girth of groups acting on metric spaces by homeomorphisms. For every non-elementary word hyperbolic group we do have such a theorem indeed (see Theorem 2.6, [Reference Akhmedov2], where the metric space is the boundary of the group, and for every hyperbolic element we have one attracting and one repelling point). In our case, the metric space is typically non-compact (in the case of Theorem
1.5
, the metric space is the non-compact space
![]() $(0,1)\cong \mathbb{R}$
), and the “hyperbolic-like” elements have several points (instead of two) which are “attractive-repelling like” within “certain compact subspace.”
$(0,1)\cong \mathbb{R}$
), and the “hyperbolic-like” elements have several points (instead of two) which are “attractive-repelling like” within “certain compact subspace.”
We would like to give a precise definition of a hyperbolic-like element.
Definition 4.3.
Let
![]() $X$
be a Hausdorff topological space,
$X$
be a Hausdorff topological space,
![]() $\Gamma$
be a subgroup of Homeo
$\Gamma$
be a subgroup of Homeo
![]() $(X)$
generated by a finite subset
$(X)$
generated by a finite subset
![]() $S\subseteq \Gamma$
,
$S\subseteq \Gamma$
,
![]() $S^{\star } = S\cup S^{-1}\cup \{1\}$
,
$S^{\star } = S\cup S^{-1}\cup \{1\}$
,
![]() $z\in X, m\in \mathbb{N}$
, and
$z\in X, m\in \mathbb{N}$
, and
![]() $\gamma \in \Gamma$
. We say
$\gamma \in \Gamma$
. We say
![]() $\gamma$
is
$\gamma$
is
![]() $(S,z,m)$
-hyperbolic-like if there exists a chain
$(S,z,m)$
-hyperbolic-like if there exists a chain
![]() $\Omega _0 \subset \Omega _1\subset \ldots \subset \Omega _m$
of finite subsets of
$\Omega _0 \subset \Omega _1\subset \ldots \subset \Omega _m$
of finite subsets of
![]() $X$
such that
$X$
such that
-
(i)
 $\Omega _0 = \{z\}$
;
$\Omega _0 = \{z\}$
; -
(ii)
 $s(\Omega _m) \cap \Omega _m = \emptyset, \forall s\in S^{\star }\backslash \{1\}$
;
$s(\Omega _m) \cap \Omega _m = \emptyset, \forall s\in S^{\star }\backslash \{1\}$
; -
(iii) for all
 $x\in (S^{\star }\backslash \{1\})\Omega _k, 0\leq k\leq m-1$
, there exist distinct
$x\in (S^{\star }\backslash \{1\})\Omega _k, 0\leq k\leq m-1$
, there exist distinct
 $p_a, p_r\in \Omega _{k+1}$
such that for all disjoint open neighborhoods
$p_a, p_r\in \Omega _{k+1}$
such that for all disjoint open neighborhoods
 $U_{p_a}, U_{p_r}$
of
$U_{p_a}, U_{p_r}$
of
 $p_a$
and
$p_a$
and
 $p_r$
, respectively, there exist
$p_r$
, respectively, there exist
 $M\in \mathbb{N}$
such that for all
$M\in \mathbb{N}$
such that for all
 $n\geq M$
,
$n\geq M$
,
 $\gamma ^{n}(x)\in U_{p_a}, \gamma ^{-n}(x)\in U_{p_r}$
.
$\gamma ^{n}(x)\in U_{p_a}, \gamma ^{-n}(x)\in U_{p_r}$
.
The proof of the following theorem utilizes the main idea of the proof of Theorem 1.5.
Theorem 4.4.
Let
![]() $X$
be a Hausdorff space,
$X$
be a Hausdorff space,
![]() $z\in X$
,
$z\in X$
,
![]() $\Gamma$
be a finitely generated subgroup of Homeo
$\Gamma$
be a finitely generated subgroup of Homeo
![]() $(X)$
,
$(X)$
,
![]() $S$
be a finite generating set of
$S$
be a finite generating set of
![]() $\Gamma$
. Assume that for all natural
$\Gamma$
. Assume that for all natural
![]() $m$
. there exists an
$m$
. there exists an
![]() $(S,z,m)$
-hyperbolic-like element of
$(S,z,m)$
-hyperbolic-like element of
![]() $\Gamma$
. Then
$\Gamma$
. Then
![]() $girth(\Gamma ) = \infty$
.
$girth(\Gamma ) = \infty$
.
Proof. Without loss of generality, we may assume that
![]() $1\notin S$
. Since
$1\notin S$
. Since
![]() $X$
is Hausdorff, the attractive and repelling points
$X$
is Hausdorff, the attractive and repelling points
![]() $p_a, p_r$
in condition (iii) are unique. By condition (ii), we also have
$p_a, p_r$
in condition (iii) are unique. By condition (ii), we also have
![]() $p_a, p_r\notin (S^{\star }\backslash \{1\})\Omega _k, 0\leq k\leq m-1$
. Then we can claim that there exists a natural number
$p_a, p_r\notin (S^{\star }\backslash \{1\})\Omega _k, 0\leq k\leq m-1$
. Then we can claim that there exists a natural number
![]() $M$
such that for all
$M$
such that for all
![]() $0\leq k\leq m-1$
, there exist unique and distinct
$0\leq k\leq m-1$
, there exist unique and distinct
![]() $p_a^{(k)}, p_r^{(k)}\in \Omega _{k+1}$
and disjoint open neighborhoods
$p_a^{(k)}, p_r^{(k)}\in \Omega _{k+1}$
and disjoint open neighborhoods
![]() $U_{p_a^{(k)}}, U_{p_r^{(k)}}$
of
$U_{p_a^{(k)}}, U_{p_r^{(k)}}$
of
![]() $p_a^{(k)}$
and
$p_a^{(k)}$
and
![]() $p_r^{(k)}$
, respectively, such that for all
$p_r^{(k)}$
, respectively, such that for all
![]() $n \gt M$
and for all
$n \gt M$
and for all
![]() $x\in (S^{\star }\backslash \{1\})\Omega _k$
,
$x\in (S^{\star }\backslash \{1\})\Omega _k$
,
![]() $\gamma ^{n}(x)\in U_{p_a^{(k)}}, \gamma ^{-n}(x)\in U_{p_r^{(k)}}$
; moreover,
$\gamma ^{n}(x)\in U_{p_a^{(k)}}, \gamma ^{-n}(x)\in U_{p_r^{(k)}}$
; moreover,
![]() $(U_{p_a^{(k)}}\sqcup U_{p_r^{(k)}})\cap (S^{\star }\backslash \{1\})\Omega _k = \emptyset$
. Then for sufficiently big
$(U_{p_a^{(k)}}\sqcup U_{p_r^{(k)}})\cap (S^{\star }\backslash \{1\})\Omega _k = \emptyset$
. Then for sufficiently big
![]() $n$
, there is no relation of length less than
$n$
, there is no relation of length less than
![]() $m-2$
among the elements of the generating set
$m-2$
among the elements of the generating set
![]() $\{\gamma, \gamma ^n\gamma _1\gamma ^n, \gamma ^{2n}\gamma _2\gamma ^{2n}, \dots, \gamma ^{sn}\gamma _s\gamma ^{sn}\}$
where
$\{\gamma, \gamma ^n\gamma _1\gamma ^n, \gamma ^{2n}\gamma _2\gamma ^{2n}, \dots, \gamma ^{sn}\gamma _s\gamma ^{sn}\}$
where
![]() $S = \{\gamma _1, \dots, \gamma _s\}$
.
$S = \{\gamma _1, \dots, \gamma _s\}$
.
Indeed, such a relation would be of the form:
where
![]() $r\leq m-2$
,
$r\leq m-2$
,
![]() $|n_i| \geq n - m, 1\leq i\leq r+1$
, and
$|n_i| \geq n - m, 1\leq i\leq r+1$
, and
![]() $\delta _i\in S^{\star }\backslash \{1\}, 1\leq i\leq r$
. Let
$\delta _i\in S^{\star }\backslash \{1\}, 1\leq i\leq r$
. Let
![]() $y\in (S^{\star }\backslash \{1\})z$
. Then for sufficiently big
$y\in (S^{\star }\backslash \{1\})z$
. Then for sufficiently big
![]() $n$
, we have
$n$
, we have
![]() $W(y)\in U_{p_a^{(r+2)}}\sqcup U_{p_r^{(r+2)}}$
. Hence,
$W(y)\in U_{p_a^{(r+2)}}\sqcup U_{p_r^{(r+2)}}$
. Hence,
![]() $W(y)\neq y$
. Since
$W(y)\neq y$
. Since
![]() $m$
is arbitrary, we conclude that
$m$
is arbitrary, we conclude that
![]() $girth(\Gamma ) = \infty$
.
$girth(\Gamma ) = \infty$
.
Remark 4.5. Theorem 4.4 generalizes Theorem 2.1 from [Reference Akhmedov2] which states that any finitely generated non-elementary subgroup of a word hyperbolic group has infinite girth.
Remark 4.6.
It is interesting that the group
![]() $F$
(the standard representation of it in
$F$
(the standard representation of it in
![]() $PL_o(I)$
) is very rich with hyperbolic-like elements, for the standard finite generating set
$PL_o(I)$
) is very rich with hyperbolic-like elements, for the standard finite generating set
![]() $S$
of
$S$
of
![]() $F$
. It is not known to us if the same can be true for a faithful representation of an elementary amenable subgroup of Homeo
$F$
. It is not known to us if the same can be true for a faithful representation of an elementary amenable subgroup of Homeo
![]() $_{+}(\mathbb{R})$
.
$_{+}(\mathbb{R})$
.
We will borrow the following definition from [Reference Akhmedov3].
Definition 4.7.
Let
![]() $\Gamma$
be a finitely generated group,
$\Gamma$
be a finitely generated group,
![]() $d(\Gamma )$
be the minimal number of a generating set of
$d(\Gamma )$
be the minimal number of a generating set of
![]() $\Gamma$
and
$\Gamma$
and
![]() $k\geq d(\Gamma )$
be a positive integer. Then, we define
$k\geq d(\Gamma )$
be a positive integer. Then, we define
![]() $girth _k(\Gamma ) = \displaystyle \sup _{\langle S \rangle = \Gamma, |S| \leq k}girth (\Gamma, S)$
.
$girth _k(\Gamma ) = \displaystyle \sup _{\langle S \rangle = \Gamma, |S| \leq k}girth (\Gamma, S)$
.
While proving Theorem 1.2, we indeed proved a bit more, namely, for any non-solvable finitely generated group
![]() $\Gamma$
of
$\Gamma$
of
![]() $PL_o(I)$
, we proved that
$PL_o(I)$
, we proved that
![]() $girth _{2d}(\Gamma ) = \infty$
where
$girth _{2d}(\Gamma ) = \infty$
where
![]() $d = d(\Gamma )$
. Also, in the proof of Theorem 1.5, we indeed proved that
$d = d(\Gamma )$
. Also, in the proof of Theorem 1.5, we indeed proved that
![]() $girth _{d+2}(\Gamma ) = \infty$
. With a slightly different argument, one can improve this result showing that
$girth _{d+2}(\Gamma ) = \infty$
. With a slightly different argument, one can improve this result showing that
![]() $girth _{d+1}(\Gamma ) = \infty$
; and in Theorem 4.4, one can prove that
$girth _{d+1}(\Gamma ) = \infty$
; and in Theorem 4.4, one can prove that
![]() $girth _{|S|+1}(\Gamma ) = \infty$
.
$girth _{|S|+1}(\Gamma ) = \infty$
.
Acknowledgment
I am thankful to Collin Bleak and Matthew Brin for useful discussions. I am also very grateful to an anonymous referee for many useful suggestions and corrections.