1. Introduction
Leonardo da Vinci (1452–1519), a luminary of the Renaissance era, was renowned not only as a painter and draftsman, but also as an engineer and fluid mechanician. Based on observations, Leonardo had illustrated many valuable concepts in modern fluid mechanics such as turbulence, the hydraulic jump and the no-slip condition (Marusic & Broomhall Reference Marusic and Broomhall2021). A notable example is the depiction of pipe flow shown in figure 1(a), where Leonardo commented: ‘The water that rises through a pipe, that which rises highest will be furthest away from the walls of the pipe’. This comment suggested that he had been aware of the no-slip boundary condition, and it could also be found in his other works, such as the drawing of an experimental water tank in figure 1(b).
Although the boundary layer had been demonstrated by Leonardo, scientific inquiry of the boundary layer had to wait until the 18th and 19th centuries, when many renowned physicists started to consider this topic, including Bernoulli, Euler, Coulomb, Darcy, Navier, Helmholtz, Poisson, Poiseuille, Stokes, Hagen, Couette, Maxwell, Prandtl and Taylor (Lauga, Brenner & Stone Reference Lauga, Brenner and Stone2007). In 1823, Navier proposed the linear boundary condition (Navier Reference Navier1823), as depicted in figure 1(c), where 
$\lambda$ is the slip length. Afterwards, Maxwell quantified the slip length of gas flowing past a solid surface (Maxwell Reference Maxwell1879), which indicated that the slip length was of the order of the mean free path of the fluid.
The definition of the boundary condition proposed by Navier and Maxwell has been widely adopted in characterising the slip properties at a fluid–solid interface. In most cases, the no-slip boundary condition (i.e. $\lambda =0$) is found to be valid. Nevertheless, the development of the surface force apparatus enables a much more precise measurement of the slip length, down to a few nanometres. From these measurements the slip length $\lambda$ is found to vary from nanometre to micrometre scales (Lauga et al. Reference Lauga, Brenner and Stone2007). As shown in figure 1(d), $\lambda$ depends on the surface roughness, surface nanobubbles, wetting properties (e.g. the contact angle $\theta$) and the shear rate $\dot {\gamma }$.
According to these experimental observations, the principal question concerns the applicability of the no-slip condition at a solid–liquid boundary, especially for complex boundaries. To better understand the slip boundary condition, Lauga & Stone (Reference Lauga and Stone2003) proposed an effective slip model, as illustrated in figure 1(e), emphasising the effect of surface heterogeneities induced by surface nanobubbles.
2. Overview
The paper by Lauga & Stone (Reference Lauga and Stone2003) considered two elementary configurations of surface heterogeneities in steady pressure-driven Stokes flow, as illustrated in figure 1(e). The pipe of radius $R$ with no-slip boundary condition (i.e. $\lambda =0$ at a fluid–solid interface) was patterned with perfect slip boundary condition (i.e. $\lambda =\infty$ at a fluid–gas interface) of width $h$ and separation $H$ in transverse and longitudinal configurations, respectively. The dimensionless spacing and percentage of the perfect slip domains are defined as $L=H/R$ and $\delta =h/H$.
The equations of incompressible Stokes flow in a circular pipe were solved numerically with the appropriate boundary conditions. Utilising analytical derivation and asymptotic approximation, the effective slip length $\lambda _{eff}$ in the longitudinal ($\lambda _{eff,\parallel }$) and transverse ($\lambda _{eff,\perp }$) directions along the pipe can be derived, as shown in table 1.
When the percentage of slip is small ($\delta \to 0$), the transverse patterns can lead to a larger effective slip length than the longitudinal patterns, $\lambda _{eff,\perp }>\lambda _{eff,\parallel }$. When the percentage of slip is large ($\delta \to 1$), the longitudinal patterns have a much more significant impact on the friction than the transverse patterns. Moreover, when the distance between the perfect slip domains is small ($L \to 0$), the slip regions are approximately two-dimensional and the shear in the longitudinal case is expected to be twice as large as the shear in the transverse case. Consequently, the slip length in the longitudinal case is double that in the transverse case, $\lambda _{eff,\parallel }=2\lambda _{eff,\perp }$.
In reality, surface heterogeneities (or slip/non-slip regions) are unlikely to be distributed in either purely transverse or purely longitudinal fashion, but may be viewed as a combination of the two. Therefore, the experimentally obtained effective slip length would be intermediate between that given by a distribution of transverse slip domains $\lambda _{eff,\perp }$ and that given by a distribution of longitudinal domains $\lambda _{eff,\parallel }$. This reflects the power of the model. It is simple yet applicable to a myriad of complicated situations. Indeed, with regard to experimentally determined slip length, the effective slip model provides a robust interpretation of the observed slip length, ensuring the applicability of the no-slip condition at a fluid–solid interface. This simple model can reproduce the sizes of slip domains that are consistent with the experimental observation of nanobubbles on hydrophobic surfaces (Tyrrell & Attard Reference Tyrrell and Attard2001) and surface roughness (Watanabe, Udagawa & Udagawa Reference Watanabe, Udagawa and Udagawa1999).
3. Impact
The work by Lauga & Stone (Reference Lauga and Stone2003) elegantly demonstrates how surface heterogeneities at the microscopic level affect the macroscopic effective slip length, and has garnered widespread recognition in the field of fluid dynamics. From a physical perspective, the concept of effective slip lays down the fundamental understanding of slip boundary conditions, especially over complex and heterogeneous boundaries.
From a practical perspective, given the inherent heterogeneity and the complex interplay of various physical parameters within experimental set-ups, the concept of effective slip offers a more coherent framework for guiding the design of surfaces, such as nanofluidics (Kavokine, Netz & Bocquet Reference Kavokine, Netz and Bocquet2021), microfluidics (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004), superhydrophobic surfaces (Quéré Reference Quéré2008) and liquid-infused surfaces (Hardt & McHale Reference Hardt and McHale2022). The slip characteristic can significantly affect fluid behaviours near the fluid–solid interface, and further affect global characteristics, including drop rebounce (Sprittles Reference Sprittles2024), drag reduction and enhanced mixing (Rothstein Reference Rothstein2010).
4. Outlook
Since the publication of Lauga & Stone (Reference Lauga and Stone2003), our understanding of the slip boundary condition over the past two decades has significantly advanced, which is partly owing to the swift progression of experimental and computational fluid dynamics (Vega-Sánchez et al. Reference Vega-Sánchez, Peppou-Chapman, Zhu and Neto2022; Hadjiconstantinou Reference Hadjiconstantinou2024) as well as the widespread existence and stability of surface nanobubbles (Lohse & Zhang Reference Lohse and Zhang2015), which were among the situations that motivated the Lauga and Stone model. From both fundamental and applied points of view, much future work remains to be done that should include multicomponent (Lyu et al. Reference Lyu, Tan, Wakata, Yang, Law, Lohse and Sun2021), multiphase, phase transition (Canale et al. Reference Canale, Comtet, Niguès, Cohen, Clanet, Siria and Bocquet2019), extreme conditions, molecular scale (Hadjiconstantinou Reference Hadjiconstantinou2024) and fluid–elastic interactions (Rallabandi Reference Rallabandi2024). It should also be stressed that the effective slip length developed in the Lauga and Stone model is very different from the microscopic slip length at the scale of individual molecules, which must be determined using molecular dynamics approaches and depends on material properties. A truly microscopic model based on a first-principles approach would be necessary to fully understand the slippery boundary problem. However, this has been a long-standing challenge due to the wide separation of length scales necessary to tackle this problem. In this context, the Lauga and Stone model provides a simple yet powerful framework for bridging the microscopic and the macroscopic.
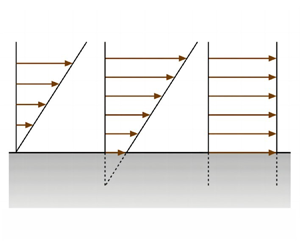
$\lambda$ and (d) experimentally determined slip length 
$\lambda$ for different surface (the contact angle 
$\theta$) and flow conditions (shear rate 
$\dot {\gamma }$), respectively, both adapted from Lauga et al. (2007). (e) Schematic drawing of the effective slip length model, adapted from Lauga & Stone (2003).
$\lambda _{eff}$ proposed by Lauga & Stone (2003).
You have
Access
1. Introduction
Leonardo da Vinci (1452–1519), a luminary of the Renaissance era, was renowned not only as a painter and draftsman, but also as an engineer and fluid mechanician. Based on observations, Leonardo had illustrated many valuable concepts in modern fluid mechanics such as turbulence, the hydraulic jump and the no-slip condition (Marusic & Broomhall Reference Marusic and Broomhall2021). A notable example is the depiction of pipe flow shown in figure 1(a), where Leonardo commented: ‘The water that rises through a pipe, that which rises highest will be furthest away from the walls of the pipe’. This comment suggested that he had been aware of the no-slip boundary condition, and it could also be found in his other works, such as the drawing of an experimental water tank in figure 1(b).
Figure 1. Leonardo da Vinci's depictions of (a) pipe flow (Royal Collection at Windsor, RCIN 919117r) and (b) water tank (Paris Manuscript I, f. 41v), both adapted from Marusic & Broomhall (Reference Marusic and Broomhall2021), from where the figures are taken with permission. (c) Illustration of the Maxwell–Navier slip length
$\lambda$ and (d) experimentally determined slip length 
$\lambda$ for different surface (the contact angle 
$\theta$) and flow conditions (shear rate 
$\dot {\gamma }$), respectively, both adapted from Lauga et al. (Reference Lauga, Brenner and Stone2007). (e) Schematic drawing of the effective slip length model, adapted from Lauga & Stone (Reference Lauga and Stone2003).
Although the boundary layer had been demonstrated by Leonardo, scientific inquiry of the boundary layer had to wait until the 18th and 19th centuries, when many renowned physicists started to consider this topic, including Bernoulli, Euler, Coulomb, Darcy, Navier, Helmholtz, Poisson, Poiseuille, Stokes, Hagen, Couette, Maxwell, Prandtl and Taylor (Lauga, Brenner & Stone Reference Lauga, Brenner and Stone2007). In 1823, Navier proposed the linear boundary condition (Navier Reference Navier1823), as depicted in figure 1(c), where
$\lambda$ is the slip length. Afterwards, Maxwell quantified the slip length of gas flowing past a solid surface (Maxwell Reference Maxwell1879), which indicated that the slip length was of the order of the mean free path of the fluid.
The definition of the boundary condition proposed by Navier and Maxwell has been widely adopted in characterising the slip properties at a fluid–solid interface. In most cases, the no-slip boundary condition (i.e.
$\lambda =0$) is found to be valid. Nevertheless, the development of the surface force apparatus enables a much more precise measurement of the slip length, down to a few nanometres. From these measurements the slip length 
$\lambda$ is found to vary from nanometre to micrometre scales (Lauga et al. Reference Lauga, Brenner and Stone2007). As shown in figure 1(d), 
$\lambda$ depends on the surface roughness, surface nanobubbles, wetting properties (e.g. the contact angle 
$\theta$) and the shear rate 
$\dot {\gamma }$.
According to these experimental observations, the principal question concerns the applicability of the no-slip condition at a solid–liquid boundary, especially for complex boundaries. To better understand the slip boundary condition, Lauga & Stone (Reference Lauga and Stone2003) proposed an effective slip model, as illustrated in figure 1(e), emphasising the effect of surface heterogeneities induced by surface nanobubbles.
2. Overview
The paper by Lauga & Stone (Reference Lauga and Stone2003) considered two elementary configurations of surface heterogeneities in steady pressure-driven Stokes flow, as illustrated in figure 1(e). The pipe of radius
$R$ with no-slip boundary condition (i.e. 
$\lambda =0$ at a fluid–solid interface) was patterned with perfect slip boundary condition (i.e. 
$\lambda =\infty$ at a fluid–gas interface) of width 
$h$ and separation 
$H$ in transverse and longitudinal configurations, respectively. The dimensionless spacing and percentage of the perfect slip domains are defined as 
$L=H/R$ and 
$\delta =h/H$.
The equations of incompressible Stokes flow in a circular pipe were solved numerically with the appropriate boundary conditions. Utilising analytical derivation and asymptotic approximation, the effective slip length
$\lambda _{eff}$ in the longitudinal (
$\lambda _{eff,\parallel }$) and transverse (
$\lambda _{eff,\perp }$) directions along the pipe can be derived, as shown in table 1.
Table 1. Summary of the effective slip length
$\lambda _{eff}$ proposed by Lauga & Stone (Reference Lauga and Stone2003).
When the percentage of slip is small (
$\delta \to 0$), the transverse patterns can lead to a larger effective slip length than the longitudinal patterns, 
$\lambda _{eff,\perp }>\lambda _{eff,\parallel }$. When the percentage of slip is large (
$\delta \to 1$), the longitudinal patterns have a much more significant impact on the friction than the transverse patterns. Moreover, when the distance between the perfect slip domains is small (
$L \to 0$), the slip regions are approximately two-dimensional and the shear in the longitudinal case is expected to be twice as large as the shear in the transverse case. Consequently, the slip length in the longitudinal case is double that in the transverse case, 
$\lambda _{eff,\parallel }=2\lambda _{eff,\perp }$.
In reality, surface heterogeneities (or slip/non-slip regions) are unlikely to be distributed in either purely transverse or purely longitudinal fashion, but may be viewed as a combination of the two. Therefore, the experimentally obtained effective slip length would be intermediate between that given by a distribution of transverse slip domains
$\lambda _{eff,\perp }$ and that given by a distribution of longitudinal domains 
$\lambda _{eff,\parallel }$. This reflects the power of the model. It is simple yet applicable to a myriad of complicated situations. Indeed, with regard to experimentally determined slip length, the effective slip model provides a robust interpretation of the observed slip length, ensuring the applicability of the no-slip condition at a fluid–solid interface. This simple model can reproduce the sizes of slip domains that are consistent with the experimental observation of nanobubbles on hydrophobic surfaces (Tyrrell & Attard Reference Tyrrell and Attard2001) and surface roughness (Watanabe, Udagawa & Udagawa Reference Watanabe, Udagawa and Udagawa1999).
3. Impact
The work by Lauga & Stone (Reference Lauga and Stone2003) elegantly demonstrates how surface heterogeneities at the microscopic level affect the macroscopic effective slip length, and has garnered widespread recognition in the field of fluid dynamics. From a physical perspective, the concept of effective slip lays down the fundamental understanding of slip boundary conditions, especially over complex and heterogeneous boundaries.
From a practical perspective, given the inherent heterogeneity and the complex interplay of various physical parameters within experimental set-ups, the concept of effective slip offers a more coherent framework for guiding the design of surfaces, such as nanofluidics (Kavokine, Netz & Bocquet Reference Kavokine, Netz and Bocquet2021), microfluidics (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004), superhydrophobic surfaces (Quéré Reference Quéré2008) and liquid-infused surfaces (Hardt & McHale Reference Hardt and McHale2022). The slip characteristic can significantly affect fluid behaviours near the fluid–solid interface, and further affect global characteristics, including drop rebounce (Sprittles Reference Sprittles2024), drag reduction and enhanced mixing (Rothstein Reference Rothstein2010).
4. Outlook
Since the publication of Lauga & Stone (Reference Lauga and Stone2003), our understanding of the slip boundary condition over the past two decades has significantly advanced, which is partly owing to the swift progression of experimental and computational fluid dynamics (Vega-Sánchez et al. Reference Vega-Sánchez, Peppou-Chapman, Zhu and Neto2022; Hadjiconstantinou Reference Hadjiconstantinou2024) as well as the widespread existence and stability of surface nanobubbles (Lohse & Zhang Reference Lohse and Zhang2015), which were among the situations that motivated the Lauga and Stone model. From both fundamental and applied points of view, much future work remains to be done that should include multicomponent (Lyu et al. Reference Lyu, Tan, Wakata, Yang, Law, Lohse and Sun2021), multiphase, phase transition (Canale et al. Reference Canale, Comtet, Niguès, Cohen, Clanet, Siria and Bocquet2019), extreme conditions, molecular scale (Hadjiconstantinou Reference Hadjiconstantinou2024) and fluid–elastic interactions (Rallabandi Reference Rallabandi2024). It should also be stressed that the effective slip length developed in the Lauga and Stone model is very different from the microscopic slip length at the scale of individual molecules, which must be determined using molecular dynamics approaches and depends on material properties. A truly microscopic model based on a first-principles approach would be necessary to fully understand the slippery boundary problem. However, this has been a long-standing challenge due to the wide separation of length scales necessary to tackle this problem. In this context, the Lauga and Stone model provides a simple yet powerful framework for bridging the microscopic and the macroscopic.
Acknowledgements
The author is indebted to C. Sun for many illuminating discussions and for his help with drafting of the manuscript.
Funding
The author acknowledges support by the National Natural Science Foundation of China under grant nos 12072144 and 12232010.
Declaration of interests
The author reports no conflict of interest.