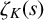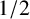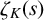1 Introduction
Let
![]() $K/\mathbb {Q}$
be a number field. The Dedekind zeta-function associated with K is defined on
$K/\mathbb {Q}$
be a number field. The Dedekind zeta-function associated with K is defined on
![]() ${\mathrm {Re}}(s)>1$
by
${\mathrm {Re}}(s)>1$
by
 $$ \begin{align*} \zeta_K(s) := \sum_{\mathfrak{a}} \frac{1}{N\mathfrak{a}^s}. \end{align*} $$
$$ \begin{align*} \zeta_K(s) := \sum_{\mathfrak{a}} \frac{1}{N\mathfrak{a}^s}. \end{align*} $$
Here,
![]() $\mathfrak {a}$
runs over all nonzero integral ideals of K. This function has an analytic continuation to
$\mathfrak {a}$
runs over all nonzero integral ideals of K. This function has an analytic continuation to
![]() $\mathbb {C}$
except for a simple pole at
$\mathbb {C}$
except for a simple pole at
![]() $s=1$
. The zeros of
$s=1$
. The zeros of
![]() $\zeta _K(s)$
in the critical strip
$\zeta _K(s)$
in the critical strip
![]() $0<{\mathrm { Re}}(s) < 1$
are called the nontrivial zeros. One of the central problems in analytic number theory is to study the order and magnitude of these nontrivial zeros. The generalised Riemann hypothesis (GRH) says that all the nontrivial zeros of
$0<{\mathrm { Re}}(s) < 1$
are called the nontrivial zeros. One of the central problems in analytic number theory is to study the order and magnitude of these nontrivial zeros. The generalised Riemann hypothesis (GRH) says that all the nontrivial zeros of
![]() $\zeta _K(s)$
lie on the vertical line
$\zeta _K(s)$
lie on the vertical line
![]() ${\mathrm {Re}}(s) = \tfrac 12$
. Under GRH, one can consider the height of a zero, that is, its distance from the point
${\mathrm {Re}}(s) = \tfrac 12$
. Under GRH, one can consider the height of a zero, that is, its distance from the point
![]() $s=\tfrac 12$
. Define
$s=\tfrac 12$
. Define
the lowest height of a nontrivial zero of
![]() $\zeta _K(s)$
other than
$\zeta _K(s)$
other than
![]() $\tfrac 12$
. It is possible that
$\tfrac 12$
. It is possible that
![]() $\zeta _K(\tfrac 12)=0$
, as shown by Armitage [Reference Armitage1] in 1971. However, it is believed that as we vary over number fields,
$\zeta _K(\tfrac 12)=0$
, as shown by Armitage [Reference Armitage1] in 1971. However, it is believed that as we vary over number fields,
![]() $\zeta _K(\tfrac 12)$
vanishes very rarely. Indeed, Soundararajan [Reference Soundararajan13] showed that for a large proportion (87.5%) of quadratic number fields,
$\zeta _K(\tfrac 12)$
vanishes very rarely. Indeed, Soundararajan [Reference Soundararajan13] showed that for a large proportion (87.5%) of quadratic number fields,
![]() $\zeta _K(\tfrac 12) \neq 0$
.
$\zeta _K(\tfrac 12) \neq 0$
.
One of the natural questions is to obtain upper and lower bounds on
![]() $\tau (K)$
. The importance of studying
$\tau (K)$
. The importance of studying
![]() $\tau (K)$
is evident from its connection to the discriminant of the number field, as highlighted in the survey paper by Odlyzko [Reference Odlyzko9]. The low-lying zeros of
$\tau (K)$
is evident from its connection to the discriminant of the number field, as highlighted in the survey paper by Odlyzko [Reference Odlyzko9]. The low-lying zeros of
![]() $\zeta _K(s)$
also have consequences for Lehmer’s conjecture on heights of algebraic numbers (see [Reference Dixit and Kala4]). In 1979, Hoffstein [Reference Hoffstein and Nathanson5] showed that for number fields K with sufficiently large degree,
$\zeta _K(s)$
also have consequences for Lehmer’s conjecture on heights of algebraic numbers (see [Reference Dixit and Kala4]). In 1979, Hoffstein [Reference Hoffstein and Nathanson5] showed that for number fields K with sufficiently large degree,
For a number field K, denote by
![]() $n_K$
the degree
$n_K$
the degree
![]() $[K:\mathbb {Q}]$
and by
$[K:\mathbb {Q}]$
and by
![]() $d_K$
the discriminant
$d_K$
the discriminant
![]() $\mbox {disc}(K/\mathbb {Q})$
. Let
$\mbox {disc}(K/\mathbb {Q})$
. Let
![]() $\alpha _K$
be the log root discriminant of K defined by
$\alpha _K$
be the log root discriminant of K defined by
In 1985, Neugebauer [Reference Neugebauer8] showed the existence of a nontrivial zero of
![]() $\zeta _K(s)$
in the rectangle
$\zeta _K(s)$
in the rectangle
for every
![]() $T\geq 50$
. Later in 1988, Neugebauer [Reference Neugebauer7] derived an explicit upper bound, namely either
$T\geq 50$
. Later in 1988, Neugebauer [Reference Neugebauer7] derived an explicit upper bound, namely either
![]() $\zeta _K(1/2)=0$
or
$\zeta _K(1/2)=0$
or
 $$ \begin{align} \tau(K) \leq \operatorname\min \bigg\{ 60, \frac{64 \pi^2}{\log \big( \frac{1}{4} \log (82 + 27 \alpha_K) \big)} \bigg\}. \end{align} $$
$$ \begin{align} \tau(K) \leq \operatorname\min \bigg\{ 60, \frac{64 \pi^2}{\log \big( \frac{1}{4} \log (82 + 27 \alpha_K) \big)} \bigg\}. \end{align} $$
Tollis [Reference Tollis14] conjectured that
 $$ \begin{align} \tau(K) \ll \frac{1}{\log |d_K|}, \end{align} $$
$$ \begin{align} \tau(K) \ll \frac{1}{\log |d_K|}, \end{align} $$
where the implied constant is absolute. Although this remains open, Sami [Reference Sami12] showed that under GRH,
 $$ \begin{align*} \tau(K) \ll_{n_K} \frac{1}{\log \log \left(\left|d_K\right|\right)}. \end{align*} $$
$$ \begin{align*} \tau(K) \ll_{n_K} \frac{1}{\log \log \left(\left|d_K\right|\right)}. \end{align*} $$
Thus, the lowest zero of the Dedekind zeta function converges to
![]() $\tfrac 12$
as we vary over number fields with a fixed degree. In [Reference Mestre6], an ineffective upper bound of a similar nature has been obtained for newforms of weight k on
$\tfrac 12$
as we vary over number fields with a fixed degree. In [Reference Mestre6], an ineffective upper bound of a similar nature has been obtained for newforms of weight k on
![]() $\Gamma _0(N)$
.
$\Gamma _0(N)$
.
Let
![]() $\tau _0:= \tau (\mathbb {Q})\, (=14.1347\ldots ) $
be the lowest zero of the Riemann zeta-function
$\tau _0:= \tau (\mathbb {Q})\, (=14.1347\ldots ) $
be the lowest zero of the Riemann zeta-function
![]() $\zeta (s)$
. Recall the famous Dedekind conjecture, which states that
$\zeta (s)$
. Recall the famous Dedekind conjecture, which states that
![]() $\zeta _K(s)/\zeta (s)$
is entire. Therefore, one expects
$\zeta _K(s)/\zeta (s)$
is entire. Therefore, one expects
![]() $\zeta _K(1/2 + i\tau _0)=0$
for all number fields K. Explicit upper bounds for the height of the lowest zero (under GRH) for automorphic L-functions were studied in [Reference Carneiro, Chandee and Milinovich3], and Bllaca [Reference Bllaca2] examined the L-functions in the Selberg class. The goal of this paper is to give a simple and effective version of Sami’s upper bound [Reference Sami12] on the first zero of the Dedekind zeta function under GRH. We obtain the following effective upper bound for the lowest zero of
$\zeta _K(1/2 + i\tau _0)=0$
for all number fields K. Explicit upper bounds for the height of the lowest zero (under GRH) for automorphic L-functions were studied in [Reference Carneiro, Chandee and Milinovich3], and Bllaca [Reference Bllaca2] examined the L-functions in the Selberg class. The goal of this paper is to give a simple and effective version of Sami’s upper bound [Reference Sami12] on the first zero of the Dedekind zeta function under GRH. We obtain the following effective upper bound for the lowest zero of
![]() $\zeta _K(s)$
.
$\zeta _K(s)$
.
Theorem 1.1. Let K be a number field such that the log root discriminant
![]() $\alpha _K> 6.6958$
and
$\alpha _K> 6.6958$
and
![]() $\zeta _K(1/2) \neq 0$
. Then, under GRH, either
$\zeta _K(1/2) \neq 0$
. Then, under GRH, either
![]() $\tau (K) \geq \tau _0$
or
$\tau (K) \geq \tau _0$
or
 $$ \begin{align*} \tau(K) \leq \frac{ \pi}{ \sqrt{2} \log (\tfrac{\alpha_K - 1.2874}{5.4084} )}. \end{align*} $$
$$ \begin{align*} \tau(K) \leq \frac{ \pi}{ \sqrt{2} \log (\tfrac{\alpha_K - 1.2874}{5.4084} )}. \end{align*} $$
Remark 1.2. One can improve this bound using Hoffstein’s result [Reference Hoffstein and Nathanson5, page 194], which states that
![]() $\tau (K) \leq 0.87$
for all number fields with sufficiently large degree. Indeed, the method of our proof shows that for number fields K with sufficiently large degree, if
$\tau (K) \leq 0.87$
for all number fields with sufficiently large degree. Indeed, the method of our proof shows that for number fields K with sufficiently large degree, if
![]() $\alpha _K> 6.4435$
, then under GRH,
$\alpha _K> 6.4435$
, then under GRH,
 $$ \begin{align*} \tau(K) \leq \frac{ \pi}{ \sqrt{2} \log ( \tfrac{\alpha_K - 1.2874}{5.1561} )}. \end{align*} $$
$$ \begin{align*} \tau(K) \leq \frac{ \pi}{ \sqrt{2} \log ( \tfrac{\alpha_K - 1.2874}{5.1561} )}. \end{align*} $$
Further, it follows from Hoffstein’s result that
![]() $\tau (K) \leq 0.37$
except for finitely many number fields with
$\tau (K) \leq 0.37$
except for finitely many number fields with
![]() $\alpha _K \leq 6.6958$
. Therefore,
$\alpha _K \leq 6.6958$
. Therefore,
 $$ \begin{align*} \tau(K) \leq \operatorname\min \left\{ 0.37, \frac{ \pi}{ \sqrt{2} \log ( \tfrac{\alpha_K - 1.2874}{5.1561} )} \right\} \end{align*} $$
$$ \begin{align*} \tau(K) \leq \operatorname\min \left\{ 0.37, \frac{ \pi}{ \sqrt{2} \log ( \tfrac{\alpha_K - 1.2874}{5.1561} )} \right\} \end{align*} $$
for all but finitely many number fields.
Assuming GRH, Sami’s bound was improved by Carneiro et al. [Reference Carneiro, Chandee and Milinovich3, Theorem 7], where they showed that as
![]() $\alpha _K \rightarrow \infty $
,
$\alpha _K \rightarrow \infty $
,
 $$ \begin{align} \tau(K) \leq \frac{\pi}{2 \log \alpha_K}+O\bigg(\frac{\log \log \alpha_K}{(\log \alpha_K)^2}\bigg). \end{align} $$
$$ \begin{align} \tau(K) \leq \frac{\pi}{2 \log \alpha_K}+O\bigg(\frac{\log \log \alpha_K}{(\log \alpha_K)^2}\bigg). \end{align} $$
Note that Theorem 1.1 yields
 $$ \begin{align*} \tau(K) \leq \frac{\pi}{\sqrt{2} \log \alpha_K}+O\bigg(\frac{1}{(\log \alpha_K)^2}\bigg). \end{align*} $$
$$ \begin{align*} \tau(K) \leq \frac{\pi}{\sqrt{2} \log \alpha_K}+O\bigg(\frac{1}{(\log \alpha_K)^2}\bigg). \end{align*} $$
So, Theorem 1.1 is weaker than (1.3) asymptotically. However, it holds for all number fields K with
![]() $\alpha _K \geq 6.6958$
without any error term.
$\alpha _K \geq 6.6958$
without any error term.
Next, we address the case where
![]() $\zeta _K(s)$
vanishes at
$\zeta _K(s)$
vanishes at
![]() $s=1/2$
.
$s=1/2$
.
Theorem 1.3. Suppose K is a number field with
![]() $\alpha _K> 12.1048 $
and
$\alpha _K> 12.1048 $
and
![]() $\zeta _K(1/2) = 0$
. Let
$\zeta _K(1/2) = 0$
. Let
 $$ \begin{align*} A :={\frac{\pi^2}{34.4} \frac{ \log \log |d_K|}{\alpha_K}}{(\alpha_K - 1.2874)} \quad\text{and}\quad B := 2 \log \bigg( \frac{\alpha_K - 1.2874}{10.8168}\bigg). \end{align*} $$
$$ \begin{align*} A :={\frac{\pi^2}{34.4} \frac{ \log \log |d_K|}{\alpha_K}}{(\alpha_K - 1.2874)} \quad\text{and}\quad B := 2 \log \bigg( \frac{\alpha_K - 1.2874}{10.8168}\bigg). \end{align*} $$
Then, under GRH, either
![]() $\tau (K) \geq \tau _0$
or
$\tau (K) \geq \tau _0$
or
 $$ \begin{align*} \tau(K) \leq \frac{\sqrt{2} \pi}{ \operatorname\min\{ A, B \}}. \end{align*} $$
$$ \begin{align*} \tau(K) \leq \frac{\sqrt{2} \pi}{ \operatorname\min\{ A, B \}}. \end{align*} $$
From Tollis’s conjecture (1.2), it is clear that over any family of number fields
![]() $\{K_i\}$
, the height of the lowest zero
$\{K_i\}$
, the height of the lowest zero
![]() $\tau (K)$
tends to
$\tau (K)$
tends to
![]() $0$
. However, in Theorems 1.1 and 1.3 (also in [Reference Sami12]), we show this for families of number fields
$0$
. However, in Theorems 1.1 and 1.3 (also in [Reference Sami12]), we show this for families of number fields
![]() $\{K_i\}$
, where the root discriminant tends to infinity. This property is also discussed in [Reference Tsfasman and Vlăduţ15, Proposition 5.2]. Also note that the bound in Theorem 1.3 is weaker than that in Theorem 1.1. This is perhaps indicative of the ‘zero repulsion’ effect due to the existing zero at
$\{K_i\}$
, where the root discriminant tends to infinity. This property is also discussed in [Reference Tsfasman and Vlăduţ15, Proposition 5.2]. Also note that the bound in Theorem 1.3 is weaker than that in Theorem 1.1. This is perhaps indicative of the ‘zero repulsion’ effect due to the existing zero at
![]() $\tfrac 12$
.
$\tfrac 12$
.
2 Preliminaries
In this section, we state and prove some results which will be useful in the proof of the main theorems. We first recall Weil’s explicit formula. Let F be a real-valued even function such that:
-
(i) F is continuously differentiable on
 $\mathbb {R}$
except at a finite number of points
$\mathbb {R}$
except at a finite number of points
 $a_i$
where
$a_i$
where
 $F(x)$
and its derivative
$F(x)$
and its derivative
 $F^{\prime }(x)$
have only discontinuities of the first kind for which F satisfies the mean condition, that is,
$F^{\prime }(x)$
have only discontinuities of the first kind for which F satisfies the mean condition, that is,  $$ \begin{align*} F(a_i)=\tfrac{1}{2}(F( a_i+0)+F(a_i-0)); \end{align*} $$
$$ \begin{align*} F(a_i)=\tfrac{1}{2}(F( a_i+0)+F(a_i-0)); \end{align*} $$
-
(ii) there exists
 $b>0$
such that
$b>0$
such that
 $F(x)$
and
$F(x)$
and
 $F^{\prime }(x)$
are
$F^{\prime }(x)$
are
 $O(e^{-(1 / 2+b)|x |})$
as
$O(e^{-(1 / 2+b)|x |})$
as
 $x\to \infty $
.
$x\to \infty $
.
Then, the Mellin transform of F, given by
is holomorphic in any strip
![]() $-a \leq \sigma \leq 1+a$
, where
$-a \leq \sigma \leq 1+a$
, where
![]() $0<a<b$
,
$0<a<b$
,
![]() $a<1$
. The following explicit formula is due to Weil [Reference Poitou10] (formulated by Poitou).
$a<1$
. The following explicit formula is due to Weil [Reference Poitou10] (formulated by Poitou).
Theorem 2.1 (Weil).
Let F satisfy conditions (i) and (ii) above with
![]() $F(0)=1$
. Then, the sum
$F(0)=1$
. Then, the sum
![]() $\sum \Phi (\rho )$
taken over the nontrivial zeros
$\sum \Phi (\rho )$
taken over the nontrivial zeros
![]() $\rho =\beta +i \gamma $
of
$\rho =\beta +i \gamma $
of
![]() $\zeta _K(s)$
with
$\zeta _K(s)$
with
![]() $|\gamma |<T$
has a limit when T tends to infinity given by the formula
$|\gamma |<T$
has a limit when T tends to infinity given by the formula
 $$ \begin{align} \sum_{\rho} \Phi(\rho) & = \Phi(0)+\Phi(1)-2 \sum_{\mathfrak{p}} \sum_{m=1}^{\infty} \frac{\log (N(\mathfrak{p }))}{N(\mathfrak{p})^{m / 2}} F(m \log (N(\mathfrak{p}))) + \log (|d_K|) \nonumber\\ &\quad - n_K [\log (2 \pi)+\gamma+2 \log (2)]-r_1 J(F)+n_K I(F), \end{align} $$
$$ \begin{align} \sum_{\rho} \Phi(\rho) & = \Phi(0)+\Phi(1)-2 \sum_{\mathfrak{p}} \sum_{m=1}^{\infty} \frac{\log (N(\mathfrak{p }))}{N(\mathfrak{p})^{m / 2}} F(m \log (N(\mathfrak{p}))) + \log (|d_K|) \nonumber\\ &\quad - n_K [\log (2 \pi)+\gamma+2 \log (2)]-r_1 J(F)+n_K I(F), \end{align} $$
where
 $$ \begin{align*} J(F)=\int_0^{\infty} \frac{F(x)}{2 \operatorname{cosh}(x / 2)} \,d x, \quad I(F)=\int_0^{\infty} \frac{1-F(x)}{2 \operatorname{sinh}(x / 2)} \,d x \end{align*} $$
$$ \begin{align*} J(F)=\int_0^{\infty} \frac{F(x)}{2 \operatorname{cosh}(x / 2)} \,d x, \quad I(F)=\int_0^{\infty} \frac{1-F(x)}{2 \operatorname{sinh}(x / 2)} \,d x \end{align*} $$
and
![]() $\gamma =0.57721566 \ldots $
denotes the Euler–Mascheroni constant. Here,
$\gamma =0.57721566 \ldots $
denotes the Euler–Mascheroni constant. Here,
![]() $\mathfrak {p}$
runs over all the prime ideals of K,
$\mathfrak {p}$
runs over all the prime ideals of K,
![]() $N(\mathfrak {p})$
denotes the ideal norm of
$N(\mathfrak {p})$
denotes the ideal norm of
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $r_1$
denotes the number of real embeddings of K.
$r_1$
denotes the number of real embeddings of K.
Observe that
 $$ \begin{align*} \Phi(0)+\Phi(1)=4 \int_0^{\infty} F(x) \operatorname{cosh}(x / 2) \,d x \text {. } \end{align*} $$
$$ \begin{align*} \Phi(0)+\Phi(1)=4 \int_0^{\infty} F(x) \operatorname{cosh}(x / 2) \,d x \text {. } \end{align*} $$
For a function
![]() $F \in L^1(\mathbb {R})$
, the Fourier transform of F is given by
$F \in L^1(\mathbb {R})$
, the Fourier transform of F is given by
Under GRH, we have
![]() $\Phi (\rho )=\widehat {F}(t)$
, where
$\Phi (\rho )=\widehat {F}(t)$
, where
![]() $\rho =1 / 2+i t$
. Set
$\rho =1 / 2+i t$
. Set
![]() $F_T(x):= F({x}/{T})$
, then
$F_T(x):= F({x}/{T})$
, then
![]() $\widehat {F}_T(u)=T \widehat {F}(T u)$
. We now recall the following lemma proved in [Reference Sami12].
$\widehat {F}_T(u)=T \widehat {F}(T u)$
. We now recall the following lemma proved in [Reference Sami12].
Lemma 2.2 (Sami).
Let F be a compactly supported even function defined on
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
 $$ \begin{align*} F(x)= \begin{cases}(1-|x|) \cos (\pi x)+\dfrac{3}{\pi} \sin (\pi |x|) & \text {if } 0 \leq |x| \leq 1, \\ 0 & \text {otherwise. }\end{cases} \end{align*} $$
$$ \begin{align*} F(x)= \begin{cases}(1-|x|) \cos (\pi x)+\dfrac{3}{\pi} \sin (\pi |x|) & \text {if } 0 \leq |x| \leq 1, \\ 0 & \text {otherwise. }\end{cases} \end{align*} $$
Then, F satisfies the growth conditions of the explicit formula and
 $$ \begin{align*} \widehat{F}(u)=2 \bigg(2-\frac{u^2}{\pi^2}\bigg)\bigg[\frac{2 \pi}{\pi^2-u^2} \cos(u/2)\bigg]^2. \end{align*} $$
$$ \begin{align*} \widehat{F}(u)=2 \bigg(2-\frac{u^2}{\pi^2}\bigg)\bigg[\frac{2 \pi}{\pi^2-u^2} \cos(u/2)\bigg]^2. \end{align*} $$
We also need the following straightforward lemma (proved by contradiction).
Lemma 2.3. Let
![]() $a, b, c$
be three positive real constants satisfying
$a, b, c$
be three positive real constants satisfying
![]() $c>2b$
. If
$c>2b$
. If
![]() $T>0$
and
$T>0$
and
![]() $a T+b e^{T / 2} \geq c$
, then
$a T+b e^{T / 2} \geq c$
, then
3 Proof of the main theorems
The proof of our theorems follows a similar method to [Reference Sami12]. We start with the following lemma.
Lemma 3.1. Let
![]() $F_T(x)=F({x}/{T})$
as in the explicit formula (2.1). Then,
$F_T(x)=F({x}/{T})$
as in the explicit formula (2.1). Then,
 $$ \begin{align*} \sum_{\mathfrak{p}}\sum_{m=1}^{\infty} \frac{\log (N(\mathfrak{p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \leq 1.2571\, n_K (2\,e^{T/2}-1), \end{align*} $$
$$ \begin{align*} \sum_{\mathfrak{p}}\sum_{m=1}^{\infty} \frac{\log (N(\mathfrak{p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \leq 1.2571\, n_K (2\,e^{T/2}-1), \end{align*} $$
where
![]() $\mathfrak {p}$
runs over all prime ideals of K.
$\mathfrak {p}$
runs over all prime ideals of K.
Proof. Let p be a rational prime. Since
![]() $ \sum _{p | \mathfrak {p}} \log N(\mathfrak {p}) \leq n_K \log p$
,
$ \sum _{p | \mathfrak {p}} \log N(\mathfrak {p}) \leq n_K \log p$
,
 $$ \begin{align*} \sum_{p | \mathfrak{p}} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m/2}} \leq n_K \frac{\log p}{p^{m/2}}. \end{align*} $$
$$ \begin{align*} \sum_{p | \mathfrak{p}} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m/2}} \leq n_K \frac{\log p}{p^{m/2}}. \end{align*} $$
From the definition of
![]() $F(x)$
, it follows that
$F(x)$
, it follows that
![]() $|F(x)| \leq 1.21$
. Hence, the above inequality gives
$|F(x)| \leq 1.21$
. Hence, the above inequality gives
 $$ \begin{align} \sum_{\mathfrak{p}, m} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m / 2}} F_T(m \log N(\mathfrak{p})) &= \sum_{m,p} \sum_{p | \mathfrak{p}} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m / 2}} F_T(m \log N(\mathfrak{p})) \nonumber \\ &\leq 1.21 \, n_K \sum_{m \log p \leq T} \frac{\log p}{p^{m / 2 }} \nonumber \\ &= 1.21 \, n_K \sum_{n \leq e^T} \frac{\Lambda(n)}{\sqrt{n}} , \end{align} $$
$$ \begin{align} \sum_{\mathfrak{p}, m} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m / 2}} F_T(m \log N(\mathfrak{p})) &= \sum_{m,p} \sum_{p | \mathfrak{p}} \frac{\log N(\mathfrak{p})}{N(\mathfrak{p})^{m / 2}} F_T(m \log N(\mathfrak{p})) \nonumber \\ &\leq 1.21 \, n_K \sum_{m \log p \leq T} \frac{\log p}{p^{m / 2 }} \nonumber \\ &= 1.21 \, n_K \sum_{n \leq e^T} \frac{\Lambda(n)}{\sqrt{n}} , \end{align} $$
where
![]() $\Lambda $
is the von Mangoldt function. Now, recall the Chebyshev function,
$\Lambda $
is the von Mangoldt function. Now, recall the Chebyshev function,
Applying partial summation and using the bound
![]() $\Psi (x) \leq 1.0389 \,x$
by Rosser and Schoenfeld [Reference Rosser and Schoenfeld11],
$\Psi (x) \leq 1.0389 \,x$
by Rosser and Schoenfeld [Reference Rosser and Schoenfeld11],
 $$ \begin{align} \sum_{n \leq e^T} \frac{\Lambda(n)}{\sqrt{n}} = \frac{\Psi(e^T)}{e^{T/2}} + \frac{1}{2} \int_1^{e^T} \frac{\Psi(t)}{t^{3/2}}\,dt &\leq 1.0389 \, ( 2 e^{T/2} - 1). \end{align} $$
$$ \begin{align} \sum_{n \leq e^T} \frac{\Lambda(n)}{\sqrt{n}} = \frac{\Psi(e^T)}{e^{T/2}} + \frac{1}{2} \int_1^{e^T} \frac{\Psi(t)}{t^{3/2}}\,dt &\leq 1.0389 \, ( 2 e^{T/2} - 1). \end{align} $$
Let
![]() $T={\sqrt {2} \pi }/{ \tau (K)}$
and let
$T={\sqrt {2} \pi }/{ \tau (K)}$
and let
![]() $F(x)$
be the function defined in Lemma 2.2. Applying Theorem 2.1 to
$F(x)$
be the function defined in Lemma 2.2. Applying Theorem 2.1 to
![]() $F_T(x)=F(x / T)$
,
$F_T(x)=F(x / T)$
,
 $$ \begin{align} \sum_{\rho} \Phi(\rho) &= \Phi_T(0)+\Phi_T(1)-2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \nonumber\\ &\quad +\log |d_K|-n_K[\log (2 \pi)+\gamma+2 \log (2)]-r_1 J(F_T)+n_K I(F_T). \end{align} $$
$$ \begin{align} \sum_{\rho} \Phi(\rho) &= \Phi_T(0)+\Phi_T(1)-2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \nonumber\\ &\quad +\log |d_K|-n_K[\log (2 \pi)+\gamma+2 \log (2)]-r_1 J(F_T)+n_K I(F_T). \end{align} $$
Since
![]() $\tau (K) \leq \tau _0$
, we have
$\tau (K) \leq \tau _0$
, we have
![]() $T \geq 0.314$
. For such T, the remaining terms on the right-hand side of (3.3) can be bounded by
$T \geq 0.314$
. For such T, the remaining terms on the right-hand side of (3.3) can be bounded by
 $$ \begin{align} \!\!\!\!\kern-1pt\!\!J(F_T) &= \int_0^{T} \frac{F(x/T)}{2 \operatorname{cosh}(x / 2)} \,d x \leq 0.276 \, e^{T/2}, \end{align} $$
$$ \begin{align} \!\!\!\!\kern-1pt\!\!J(F_T) &= \int_0^{T} \frac{F(x/T)}{2 \operatorname{cosh}(x / 2)} \,d x \leq 0.276 \, e^{T/2}, \end{align} $$
 $$ \begin{align} I(F_T) &= \int_0^{T} \frac{1-F(x/T)}{2 \operatorname{sinh}(x / 2)} \,d x \geq -0.1034 \, e^{T/2}. \end{align} $$
$$ \begin{align} I(F_T) &= \int_0^{T} \frac{1-F(x/T)}{2 \operatorname{sinh}(x / 2)} \,d x \geq -0.1034 \, e^{T/2}. \end{align} $$
We are now ready to prove our theorems.
Proof of Theorem 1.1.
Since
![]() $\zeta _K(1/2) \neq 0$
, (3.3) gives
$\zeta _K(1/2) \neq 0$
, (3.3) gives
 $$ \begin{align*} \log |d_K| + \Phi_T(0)+\Phi_T(1) &\leq 2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \\ &\quad + n_K[\log (2 \pi)+\gamma+2 \log (2)] + r_1 J\left(F_T\right)-n_K I(F_T). \end{align*} $$
$$ \begin{align*} \log |d_K| + \Phi_T(0)+\Phi_T(1) &\leq 2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) \\ &\quad + n_K[\log (2 \pi)+\gamma+2 \log (2)] + r_1 J\left(F_T\right)-n_K I(F_T). \end{align*} $$
From Lemma 2.2 along with (3.4) and (3.5),
Thus,
![]() $ \alpha _K - 1.2874 \leq 5.4084 \,e^{T/2}$
and, for
$ \alpha _K - 1.2874 \leq 5.4084 \,e^{T/2}$
and, for
![]() $\alpha _K> 6.6958$
,
$\alpha _K> 6.6958$
,
Since
![]() $T={\sqrt {2}\pi }/{\tau (K)}$
, the theorem follows.
$T={\sqrt {2}\pi }/{\tau (K)}$
, the theorem follows.
Proof of Theorem 1.3.
Here,
![]() $\zeta _K(\tfrac 12)=0$
and therefore (3.3) gives
$\zeta _K(\tfrac 12)=0$
and therefore (3.3) gives
 $$ \begin{align*} \log |d_K| + \Phi_T(0) & +\Phi_T(1) \leq 2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) + \\ &\quad + n_K[\log (2 \pi)+\gamma+2 \log (2)] + r_1 J(F_T)-n_K I(F_T) + \frac{16}{\pi^2}rT, \end{align*} $$
$$ \begin{align*} \log |d_K| + \Phi_T(0) & +\Phi_T(1) \leq 2 \sum_{\mathfrak{p}, m} \frac{\log (N(\mathfrak {p}))}{N(\mathfrak{p})^{m / 2}} F_T(m \log (N(\mathfrak{p}))) + \\ &\quad + n_K[\log (2 \pi)+\gamma+2 \log (2)] + r_1 J(F_T)-n_K I(F_T) + \frac{16}{\pi^2}rT, \end{align*} $$
where r is the order of
![]() $\zeta _K(s)$
at
$\zeta _K(s)$
at
![]() $1/2$
. As before, using Lemma 2.2 along with (3.4) and (3.5),
$1/2$
. As before, using Lemma 2.2 along with (3.4) and (3.5),
From [Reference Sami12, Proposition 1], we can bound the order of the zero of
![]() $\zeta _K(s)$
at
$\zeta _K(s)$
at
![]() $s=1/2$
by
$s=1/2$
by
 $$ \begin{align*} r \leq \frac{\log |d_K|}{\log \log |d_K|} + \frac{n_K}{2 \log \log |d_K|}. \end{align*} $$
$$ \begin{align*} r \leq \frac{\log |d_K|}{\log \log |d_K|} + \frac{n_K}{2 \log \log |d_K|}. \end{align*} $$
Thus,
 $$ \begin{align*} \alpha_K - 1.2874 & \leq 5.4084 \, e^{T/2} + \bigg( \frac{17.2}{\pi^2}\frac{\alpha_K} {\log \log |d_K|} \bigg) T. \end{align*} $$
$$ \begin{align*} \alpha_K - 1.2874 & \leq 5.4084 \, e^{T/2} + \bigg( \frac{17.2}{\pi^2}\frac{\alpha_K} {\log \log |d_K|} \bigg) T. \end{align*} $$
Using Lemma 2.3 with
 $$ \begin{align*}a=\bigg( \frac{17.2}{\pi^2}\frac{\alpha_K} {\log \log |d_K|} \bigg), \quad b=5.4084, \quad c=\alpha_K - 1.2874,\end{align*} $$
$$ \begin{align*}a=\bigg( \frac{17.2}{\pi^2}\frac{\alpha_K} {\log \log |d_K|} \bigg), \quad b=5.4084, \quad c=\alpha_K - 1.2874,\end{align*} $$
we conclude that
 $$ \begin{align*} \tau(K) \leq \frac{\sqrt{2} \pi}{ \operatorname\min\{ A, B \}}, \end{align*} $$
$$ \begin{align*} \tau(K) \leq \frac{\sqrt{2} \pi}{ \operatorname\min\{ A, B \}}, \end{align*} $$
where
![]() $A,B$
are as in the statement of the theorem. This completes the proof.
$A,B$
are as in the statement of the theorem. This completes the proof.
4 Computational data and concluding remarks
Let
![]() $K=\mathbb {Q}(\beta )$
be a number field and
$K=\mathbb {Q}(\beta )$
be a number field and
![]() $m_{\beta }(x)$
be the minimal polynomial of
$m_{\beta }(x)$
be the minimal polynomial of
![]() $\beta $
. Using SageMath, we can compare the lowest zero and the bounds obtained using Theorem 1.1 (see Table 1).
$\beta $
. Using SageMath, we can compare the lowest zero and the bounds obtained using Theorem 1.1 (see Table 1).
Table 1 Comparing the bound in Theorem 1.1 with the height of the first zero.

However, we can also compare Theorem 1.1 with Neugebaur’s bound in (1.1). Although the bound in (1.1) is unconditional, it applies only for the cases where
![]() $\alpha _K$
is very large
$\alpha _K$
is very large
![]() $(> 10^{64849})$
, whereas Theorem 1.1 applies for all K with
$(> 10^{64849})$
, whereas Theorem 1.1 applies for all K with
![]() $\alpha _K \geq 6.6958$
.
$\alpha _K \geq 6.6958$
.
Acknowledgements
I would like to thank the referee for carefully going through the paper and providing useful comments and suggestions. I thank my advisor Dr. Anup Dixit for several fruitful discussions. I am grateful to Dr. Siddhi Pathak for pointing out the result of Hoffstein in [Reference Hoffstein and Nathanson5]. I also thank Prof. Jeffery Hoffstein for his support and encouragement.