1. Introduction
Wall-shear stress fluctuation is a crucial physical quantity in wall-bounded turbulence, as it is of importance for noise radiation, structural vibration, drag generation and wall heat transfer, among others (Diaz-Daniel, Laizet & Vassilicos Reference Diaz-Daniel, Laizet and Vassilicos2017; Cheng et al. Reference Cheng, Li, Lozano-Durán and Liu2020). In the past two decades, ample evidence has shown that the root-mean-squared value of streamwise wall-shear stress fluctuations (![]() $\tau _{x,rms}^{'}$) is sensitive to the flow Reynolds number (Abe, Kawamura & Choi Reference Abe, Kawamura and Choi2004; Schlatter & Örlü Reference Schlatter and Örlü2010; Yang & Lozano-Durán Reference Yang and Lozano-Durán2017; Guerrero, Lambert & Chin Reference Guerrero, Lambert and Chin2020). It indicates that large-scale energy-containing eddies populating the logarithmic and outer regions in high-Reynolds-number wall turbulence have non-negligible influences on the near-wall turbulence dynamics, and thus the wall friction (de Giovanetti, Hwang & Choi Reference de Giovanetti, Hwang and Choi2016; Li et al. Reference Li, Fan, Modesti and Cheng2019).
$\tau _{x,rms}^{'}$) is sensitive to the flow Reynolds number (Abe, Kawamura & Choi Reference Abe, Kawamura and Choi2004; Schlatter & Örlü Reference Schlatter and Örlü2010; Yang & Lozano-Durán Reference Yang and Lozano-Durán2017; Guerrero, Lambert & Chin Reference Guerrero, Lambert and Chin2020). It indicates that large-scale energy-containing eddies populating the logarithmic and outer regions in high-Reynolds-number wall turbulence have non-negligible influences on the near-wall turbulence dynamics, and thus the wall friction (de Giovanetti, Hwang & Choi Reference de Giovanetti, Hwang and Choi2016; Li et al. Reference Li, Fan, Modesti and Cheng2019).
Until now, several models have been proposed on the organization of motions in logarithmic and outer regions and their interactions with the near-wall dynamics. Marusic, Mathis & Hutchins (Reference Marusic, Mathis and Hutchins2010) have established that superposition and modulation are the two basic mechanisms that large-scale motions (LSM) and very-large-scale motions (VLSM) exert influences on the near-wall turbulence. The former refers to the footprints of LSM and VLSM on the near-wall turbulence, while the latter indicates the intensity amplification or attenuation of near-wall small-scale turbulence by the outer motions. Mathis et al. (Reference Mathis, Marusic, Chernyshenko and Hutchins2013) extended the model to interpret the generation of wall-shear stress fluctuations in high-Reynolds-number flows. They emphasized that superposition and modulation are still two essential factors. This inner–outer interaction model (IOIM) has also been successfully developed to predict the near-wall velocity fluctuations with data inputs from the log layer (Marusic et al. Reference Marusic, Mathis and Hutchins2010; Baars, Hutchins & Marusic Reference Baars, Hutchins and Marusic2016; Wang, Hu & Zheng Reference Wang, Hu and Zheng2021).
On the other hand, the most elegant conceptual model describing the motions in the logarithmic region is the attached-eddy model (AEM) (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982). It conjectures that the logarithmic region is occupied by an array of self-similar energy-containing motions (or eddies) with their roots attached to the near-wall region. Extensive validations support the existence of attached eddies in high-Reynolds-number turbulence, such as the logarithmic decaying of streamwise velocity fluctuation intensities (Meneveau & Marusic Reference Meneveau and Marusic2013), as originally predicted by Townsend (Reference Townsend1976). The reader is referred to a recent review work by Marusic & Monty (Reference Marusic and Monty2019) for more details. Given the existence of wall-attached energy-containing motions in the logarithmic region, it would be quite natural to hypothesize that the near-wall part of these motions would affect the generation of the wall-shear fluctuations to some extent, maybe, via the superposition and modulation mechanisms. However, some fundamental questions may be raised, e.g. whether the IOIM and AEM are consistent with each other? There's a possibility that the superposition component of ![]() $\tau _x'$ decomposed by the IOIM in physical space cannot fully follow the predictions made by the AEM quantitatively. If yes, whether these two models can shed light on the mechanism of wall-shear fluctuation generation and be indicative for modelling approaches?
$\tau _x'$ decomposed by the IOIM in physical space cannot fully follow the predictions made by the AEM quantitatively. If yes, whether these two models can shed light on the mechanism of wall-shear fluctuation generation and be indicative for modelling approaches?
Previous study (Yang & Lozano-Durán Reference Yang and Lozano-Durán2017) verified that the generation of wall-shear stress fluctuations can be interpreted as the outcomes of the momentum cascade across momentum-carried eddies of different scales, and modelled by an additive process. Here, we first aim to couple the additive description with the AEM to portray the generation process of streamwise wall-shear fluctuations, resulting from wall-attached eddies. Two scaling laws describing their intensities and the linkages with the characteristic scales of attached eddies can be derived (the characteristic scales of attached eddies are their wall-normal heights according to AEM (Townsend Reference Townsend1976)). Then, we intend to isolate the streamwise wall-shear stress fluctuations generated by attached eddies in a turbulent channel flow at ![]() $Re_{\tau }=2003$ (
$Re_{\tau }=2003$ (![]() $Re_{\tau }=hu_{\tau }/\nu$,
$Re_{\tau }=hu_{\tau }/\nu$, ![]() $h$ denotes the channel half-height,
$h$ denotes the channel half-height, ![]() $u_{\tau }$ the wall friction velocity and
$u_{\tau }$ the wall friction velocity and ![]() $\nu$ the kinematic viscosity) by resorting to the IOIM (Marusic et al. Reference Marusic, Mathis and Hutchins2010; Baars et al. Reference Baars, Hutchins and Marusic2016). Here, the IOIM is employed as a tool to estimate the streamwise wall-shear fluctuations generated by attached eddies. The statistics from the IOIM can be processed to verify the scaling laws deduced by the AEM, so as to demonstrate their consistency. Moreover, a simple algebraic model describing the instantaneous distributions of the streamwise wall-shear stress fluctuations generated by attached eddies will be proposed.
$\nu$ the kinematic viscosity) by resorting to the IOIM (Marusic et al. Reference Marusic, Mathis and Hutchins2010; Baars et al. Reference Baars, Hutchins and Marusic2016). Here, the IOIM is employed as a tool to estimate the streamwise wall-shear fluctuations generated by attached eddies. The statistics from the IOIM can be processed to verify the scaling laws deduced by the AEM, so as to demonstrate their consistency. Moreover, a simple algebraic model describing the instantaneous distributions of the streamwise wall-shear stress fluctuations generated by attached eddies will be proposed.
2. Streamwise wall-shear stress fluctuations generated by attached eddies
According to Mandelbrot (Reference Mandelbrot1974) and Yang & Lozano-Durán (Reference Yang and Lozano-Durán2017), the generation of streamwise wall-stress fluctuations can be modelled as an additive process within multifractal formalism, which takes the form of
 \begin{equation} \tau_{x}^{'+}=\sum_{i=1}^{n}a_i, \end{equation}
\begin{equation} \tau_{x}^{'+}=\sum_{i=1}^{n}a_i, \end{equation}
where ![]() $a_i$ are random addends, representing an increment in
$a_i$ are random addends, representing an increment in ![]() $\tau _x^{'+}$ due to eddies with wall-normal height
$\tau _x^{'+}$ due to eddies with wall-normal height ![]() $h/2^i$, and superscript
$h/2^i$, and superscript ![]() $+$ denotes the normalization with wall units. Here, we intend to isolate the contributions from the eddies populating the logarithmic region (
$+$ denotes the normalization with wall units. Here, we intend to isolate the contributions from the eddies populating the logarithmic region (![]() $\tau _{x,o}^{'+}$) and link to their wall-normal positions
$\tau _{x,o}^{'+}$) and link to their wall-normal positions ![]() $y$. Here,
$y$. Here, ![]() $\tau _{x,o}^{'+}$ can be expressed as
$\tau _{x,o}^{'+}$ can be expressed as
 \begin{equation} \tau_{x,o}^{'+}=\sum_{i=n_s}^{n_o}a_i, \end{equation}
\begin{equation} \tau_{x,o}^{'+}=\sum_{i=n_s}^{n_o}a_i, \end{equation}
where ![]() $n_s$ and
$n_s$ and ![]() $n_o$ represent the additives that correspond to the eddies with the wall-normal height at
$n_o$ represent the additives that correspond to the eddies with the wall-normal height at ![]() $y_s$ and
$y_s$ and ![]() $y_o$, respectively. Here,
$y_o$, respectively. Here, ![]() $y_s$ is the lower bound of the logarithmic region, and generally believed to be
$y_s$ is the lower bound of the logarithmic region, and generally believed to be ![]() $80 \leq y_s^+\leq 100$ (Jiménez Reference Jiménez2018; Baars & Marusic Reference Baars and Marusic2020);
$80 \leq y_s^+\leq 100$ (Jiménez Reference Jiménez2018; Baars & Marusic Reference Baars and Marusic2020); ![]() $y_o$ is the outer reference height. It can be found that
$y_o$ is the outer reference height. It can be found that ![]() $1< n_s < n_o < n$. The addends
$1< n_s < n_o < n$. The addends ![]() $a_i$ are assumed to be identically and independently distributed (i.i.d.) and equal to
$a_i$ are assumed to be identically and independently distributed (i.i.d.) and equal to ![]() $a$. The number of the addends should be proportional to
$a$. The number of the addends should be proportional to
where ![]() $p(y)$ is the eddy population density, which is proportional to
$p(y)$ is the eddy population density, which is proportional to ![]() $1/y$ according to the AEM (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982). A momentum generation function
$1/y$ according to the AEM (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982). A momentum generation function ![]() $\langle \exp (q\tau _{x,o}^{'+})\rangle$, where
$\langle \exp (q\tau _{x,o}^{'+})\rangle$, where ![]() $\langle \; \rangle$ represents the averaging in the temporal and spatially homogeneous directions, is defined to scrutinize the scaling behaviour of
$\langle \; \rangle$ represents the averaging in the temporal and spatially homogeneous directions, is defined to scrutinize the scaling behaviour of ![]() $\tau _{x,o}^{'+}$ (Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016). Here,
$\tau _{x,o}^{'+}$ (Yang, Marusic & Meneveau Reference Yang, Marusic and Meneveau2016). Here, ![]() $\langle \exp (q\tau _{x,o}^{'+})\rangle$ can be evaluated as
$\langle \exp (q\tau _{x,o}^{'+})\rangle$ can be evaluated as
 \begin{equation} \left\langle \exp(q\tau_{x,o}^{'+})\right\rangle=\left\langle \exp(qa)\right\rangle^{n_o-n_s+1}\sim \left(\frac{y_o}{y_s}\right)^{s(q)}, \end{equation}
\begin{equation} \left\langle \exp(q\tau_{x,o}^{'+})\right\rangle=\left\langle \exp(qa)\right\rangle^{n_o-n_s+1}\sim \left(\frac{y_o}{y_s}\right)^{s(q)}, \end{equation}
where ![]() $q$ is a real number,
$q$ is a real number, ![]() $s(q)=C_1\ln \langle \exp (qa)\rangle$ is called the anomalous exponent and
$s(q)=C_1\ln \langle \exp (qa)\rangle$ is called the anomalous exponent and ![]() $C_1$ is a constant. Equation (2.4) is called strong self-similarity (SSS). If
$C_1$ is a constant. Equation (2.4) is called strong self-similarity (SSS). If ![]() $a$ is a Gaussian variable, the anomalous exponent can be recast as
$a$ is a Gaussian variable, the anomalous exponent can be recast as
where ![]() $C_2$ is another constant. On the other hand, an extended self-similarity (ESS) is defined to describe the relationship between
$C_2$ is another constant. On the other hand, an extended self-similarity (ESS) is defined to describe the relationship between ![]() $\langle \exp (q\tau _{x,o}^{'+})\rangle$ and
$\langle \exp (q\tau _{x,o}^{'+})\rangle$ and ![]() $\langle \exp (q_0\tau _{x,o}^{'+})\rangle$ (fixed
$\langle \exp (q_0\tau _{x,o}^{'+})\rangle$ (fixed ![]() $q_0$) (Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993), i.e.
$q_0$) (Benzi et al. Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993), i.e.
where ![]() $\xi (q,q_0)$ is a function of
$\xi (q,q_0)$ is a function of ![]() $q$ (fixed
$q$ (fixed ![]() $q_0$). Note that ESS does not strictly rely on the identically and independently distribution of the addends, but the additive process (2.2).
$q_0$). Note that ESS does not strictly rely on the identically and independently distribution of the addends, but the additive process (2.2).
3. DNS database and scale decomposition method
The direct numerical simulation (DNS) database used in the present study is an incompressible turbulent channel flow at ![]() $Re_{\tau }=2003$, which has been extensively validated by previous studies (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Jiménez & Hoyas Reference Jiménez and Hoyas2008). The decomposition of
$Re_{\tau }=2003$, which has been extensively validated by previous studies (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Jiménez & Hoyas Reference Jiménez and Hoyas2008). The decomposition of ![]() $\tau '_x$ is based on the IOIM first proposed by Marusic et al. (Reference Marusic, Mathis and Hutchins2010). Baars et al. (Reference Baars, Hutchins and Marusic2016) modified the computational process by introducing spectral stochastic estimation to avoid artificial scale decomposition. In this work, the modified version of the IOIM is adopted to investigate the multiscale characteristics of
$\tau '_x$ is based on the IOIM first proposed by Marusic et al. (Reference Marusic, Mathis and Hutchins2010). Baars et al. (Reference Baars, Hutchins and Marusic2016) modified the computational process by introducing spectral stochastic estimation to avoid artificial scale decomposition. In this work, the modified version of the IOIM is adopted to investigate the multiscale characteristics of ![]() $\tau '_x$. It can be expressed as
$\tau '_x$. It can be expressed as
 \begin{equation} u_{p}^{+}\left(y^{+}\right)=\underbrace{u^{*}\left(y^{+}\right)\left\{1+\varGamma_{u u} u_{L}^{+}\left(y^{+}\right)\right\}}_{u_{s}^{+}}+u_{L}^{+}\left(y^{+}\right), \end{equation}
\begin{equation} u_{p}^{+}\left(y^{+}\right)=\underbrace{u^{*}\left(y^{+}\right)\left\{1+\varGamma_{u u} u_{L}^{+}\left(y^{+}\right)\right\}}_{u_{s}^{+}}+u_{L}^{+}\left(y^{+}\right), \end{equation}
where ![]() $u_{p}^{+}$ denotes the predicted near-wall streamwise velocity fluctuation,
$u_{p}^{+}$ denotes the predicted near-wall streamwise velocity fluctuation, ![]() $u^{*}$ denotes the universal velocity signal without large-scale impact,
$u^{*}$ denotes the universal velocity signal without large-scale impact, ![]() $u_L^{+}$ is the superposition component,
$u_L^{+}$ is the superposition component, ![]() $\varGamma _{u u}$ is the amplitude-modulation coefficient and
$\varGamma _{u u}$ is the amplitude-modulation coefficient and ![]() $u_{s}^{+}$ denotes the amplitude modulation of the universal signal
$u_{s}^{+}$ denotes the amplitude modulation of the universal signal ![]() $u^{*}$. Here,
$u^{*}$. Here, ![]() $u_{L}^{+}$ is obtained by spectral stochastic estimation of the streamwise velocity fluctuation at the logarithmic region
$u_{L}^{+}$ is obtained by spectral stochastic estimation of the streamwise velocity fluctuation at the logarithmic region ![]() $y_o^+$, namely,
$y_o^+$, namely,
where ![]() $u_{o}^{+}$ is the streamwise velocity fluctuation at
$u_{o}^{+}$ is the streamwise velocity fluctuation at ![]() $y_o^+$ in the logarithmic region and
$y_o^+$ in the logarithmic region and ![]() $F_x$ and
$F_x$ and ![]() $F_x^{-1}$ denote the fast Fourier transform and the inverse fast Fourier transform in the streamwise direction, respectively. Here,
$F_x^{-1}$ denote the fast Fourier transform and the inverse fast Fourier transform in the streamwise direction, respectively. Here, ![]() $H_L$ is the transfer kernel, which evaluates the correlation between
$H_L$ is the transfer kernel, which evaluates the correlation between ![]() $u^+(y^+)$ and
$u^+(y^+)$ and ![]() $u_{o}^{+}(y_o^+)$ at a given length scale
$u_{o}^{+}(y_o^+)$ at a given length scale ![]() $\lambda _{x}^{+}$, and can be calculated as
$\lambda _{x}^{+}$, and can be calculated as
 \begin{equation} H_{L}\left(\lambda_{x}^{+}, y^{+}\right)=\frac{\left\langle\hat{u}\left(\lambda_{x}^{+}, y^{+}, z^{+}\right) \overline{\hat{u}_o}\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right)\right\rangle}{\left\langle\hat{u}_o\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right) \overline{\hat{u}_o}\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right)\right\rangle}, \end{equation}
\begin{equation} H_{L}\left(\lambda_{x}^{+}, y^{+}\right)=\frac{\left\langle\hat{u}\left(\lambda_{x}^{+}, y^{+}, z^{+}\right) \overline{\hat{u}_o}\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right)\right\rangle}{\left\langle\hat{u}_o\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right) \overline{\hat{u}_o}\left(\lambda_{x}^{+}, y_{o}^{+}, z^{+}\right)\right\rangle}, \end{equation}
where ![]() $\hat {u}$ is the Fourier coefficient of
$\hat {u}$ is the Fourier coefficient of ![]() $u$, and
$u$, and ![]() $\bar {\hat {u}}$ is the complex conjugate of
$\bar {\hat {u}}$ is the complex conjugate of ![]() $\hat {u}$.
$\hat {u}$.
In this work, we mainly pay attention to the quantity, ![]() $\tau '_x$ generated by the attached eddies. Thus, the predicted position
$\tau '_x$ generated by the attached eddies. Thus, the predicted position ![]() $y^+$ is fixed at
$y^+$ is fixed at ![]() $y^+=0.3$, and the outer reference height
$y^+=0.3$, and the outer reference height ![]() $y_o^+$ varies from
$y_o^+$ varies from ![]() $100$ (namely
$100$ (namely ![]() $y_s^+$) to
$y_s^+$) to ![]() $0.2h^+$ (denoted as
$0.2h^+$ (denoted as ![]() $y_e^+$), i.e. the upper boundary of the logarithmic region (Jiménez Reference Jiménez2018). We have checked that as long as the predicted position is around
$y_e^+$), i.e. the upper boundary of the logarithmic region (Jiménez Reference Jiménez2018). We have checked that as long as the predicted position is around ![]() $y^+\le O(1)$, the results presented below are insensitive to the choice of specific
$y^+\le O(1)$, the results presented below are insensitive to the choice of specific ![]() $y^+$. Once
$y^+$. Once ![]() $u_L^+$ is obtained, the superposition component of
$u_L^+$ is obtained, the superposition component of ![]() $\tau _x^{'+}$ can be calculated by definition (i.e.
$\tau _x^{'+}$ can be calculated by definition (i.e. ![]() ${\partial u_L^{'+}}/{\partial y^+}$ at the wall) and denoted as
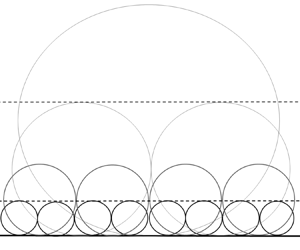
${\partial u_L^{'+}}/{\partial y^+}$ at the wall) and denoted as ![]() $\tau _{x,L}^{'+}(y_o^+)$. According to the hierarchical attached eddies in high-Reynolds-number wall turbulence (see figure 1),
$\tau _{x,L}^{'+}(y_o^+)$. According to the hierarchical attached eddies in high-Reynolds-number wall turbulence (see figure 1), ![]() $\tau _{x,L}^{'+}(y_o^+)$ represents the superposition contributed from the wall-coherent motions with their height larger than
$\tau _{x,L}^{'+}(y_o^+)$ represents the superposition contributed from the wall-coherent motions with their height larger than ![]() $y_o^+$. Thus, the difference value
$y_o^+$. Thus, the difference value ![]() $\tau _{x,L}^{'+}(y_s^+)-\tau _{x,L}^{'+}(y_o^+)$ can be interpreted as the superposition contribution generated by the wall-coherent eddies with their wall-normal heights within
$\tau _{x,L}^{'+}(y_s^+)-\tau _{x,L}^{'+}(y_o^+)$ can be interpreted as the superposition contribution generated by the wall-coherent eddies with their wall-normal heights within ![]() $y_s^+$ and
$y_s^+$ and ![]() $y_o^+$, i.e.
$y_o^+$, i.e. ![]() $\tau _{x,o}^{'+}$ in (2.2). Considering that
$\tau _{x,o}^{'+}$ in (2.2). Considering that ![]() $y_s^+$ is the lower bound of the logarithmic region, the increase of
$y_s^+$ is the lower bound of the logarithmic region, the increase of ![]() $y_o^+$ corresponds to the enlargement of the addends in the additive description (see (2.2)). In this way, the connection between the AEM and the IOIM are established, and the AEM predictions (see (2.4)–(2.6)) can be verified directly.
$y_o^+$ corresponds to the enlargement of the addends in the additive description (see (2.2)). In this way, the connection between the AEM and the IOIM are established, and the AEM predictions (see (2.4)–(2.6)) can be verified directly.

Figure 1. A schematic of the AEM (Hwang Reference Hwang2015). Each circle represents an individual attached eddy. Here, ![]() $y_s^+$ and
$y_s^+$ and ![]() $y_e^+$ are the lower and upper bounds of the logarithmic region, respectively;
$y_e^+$ are the lower and upper bounds of the logarithmic region, respectively; ![]() $y_0^+$ is the outer reference height, and varies from
$y_0^+$ is the outer reference height, and varies from ![]() $y_s^+$ to
$y_s^+$ to ![]() $y_e^+$.
$y_e^+$.
4. Results and discussion
4.1. Scaling laws of  $\tau _{x,o}^{'+}$
$\tau _{x,o}^{'+}$
Here, we further define a moment generation function based on the IOIM. It takes the form of
Figure 2(a) shows the variations of ![]() $G$ as a function of
$G$ as a function of ![]() $y_o/y_s$ for
$y_o/y_s$ for ![]() $q=\pm 5$ and
$q=\pm 5$ and ![]() $q=\pm 3$. Power-law behaviours can be found in the interval between
$q=\pm 3$. Power-law behaviours can be found in the interval between ![]() $1.7\le y_o/y_s\le 2.9$ for positive
$1.7\le y_o/y_s\le 2.9$ for positive ![]() $q$ and
$q$ and ![]() $1.7\le y_o/y_s\le 4$ for negative
$1.7\le y_o/y_s\le 4$ for negative ![]() $q$, justifying the validity of SSS, i.e. (2.4). Figure 2(b) is in aid of accessing the scalings by displaying the variations of premultiplied
$q$, justifying the validity of SSS, i.e. (2.4). Figure 2(b) is in aid of accessing the scalings by displaying the variations of premultiplied ![]() $G$. This observation highlights that the superpositions of wall-attached log-region motions on wall surface follow the additive process, characterized by (2.2). It is also worth mentioning that the power-law behaviour can be observed for larger wall-normal intervals for negative
$G$. This observation highlights that the superpositions of wall-attached log-region motions on wall surface follow the additive process, characterized by (2.2). It is also worth mentioning that the power-law behaviour can be observed for larger wall-normal intervals for negative ![]() $q$. As
$q$. As ![]() $G(q,y_o^+)$ quantifies
$G(q,y_o^+)$ quantifies ![]() $\tau _{x,L}^{'+}(y_s^+)-\tau _{x,L}^{'+}(y_o^+)$, which features the same sign as
$\tau _{x,L}^{'+}(y_s^+)-\tau _{x,L}^{'+}(y_o^+)$, which features the same sign as ![]() $q$, this observation is consistent with the work of Cheng et al. (Reference Cheng, Li, Lozano-Durán and Liu2020), which showed that the footprints of the inactive part of attached eddies populating the logarithmic region are actively connected with large-scale negative
$q$, this observation is consistent with the work of Cheng et al. (Reference Cheng, Li, Lozano-Durán and Liu2020), which showed that the footprints of the inactive part of attached eddies populating the logarithmic region are actively connected with large-scale negative ![]() $\tau '_x$. Other
$\tau '_x$. Other ![]() $q$ values yield similar results and are not shown here for brevity.
$q$ values yield similar results and are not shown here for brevity.

Figure 2. (a) ![]() $G$ as functions of
$G$ as functions of ![]() $y_o/y_s$ for
$y_o/y_s$ for ![]() $q=\pm 5$ and
$q=\pm 5$ and ![]() $q=\pm 3$; (b) premultiplied
$q=\pm 3$; (b) premultiplied ![]() $G$ as functions of
$G$ as functions of ![]() $y_o/y_s$ for
$y_o/y_s$ for ![]() $q=\pm 5$ and
$q=\pm 5$ and ![]() $q=\pm 3$.
$q=\pm 3$.
The anomalous exponent ![]() $s(q)$ can be obtained by fitting the range
$s(q)$ can be obtained by fitting the range ![]() $2\le y_o/y_s\le 2.9$, where both positive and negative
$2\le y_o/y_s\le 2.9$, where both positive and negative ![]() $q$ display good power-law scalings. Figure 3(a) displays the variation of the anomalous exponent
$q$ display good power-law scalings. Figure 3(a) displays the variation of the anomalous exponent ![]() $s(q)$ as a function of
$s(q)$ as a function of ![]() $q$. The solid line denotes the quadratic fit within
$q$. The solid line denotes the quadratic fit within ![]() $-0.5\le q \le 0.5$. It can be seen that the variation of
$-0.5\le q \le 0.5$. It can be seen that the variation of ![]() $s(q)$ is very close to the model prediction, i.e. the quadratic function as (2.5) with
$s(q)$ is very close to the model prediction, i.e. the quadratic function as (2.5) with ![]() $C_2=0.00629$. Only minor discrepancies between DNS data and model predictions can be observed. As such, it is reasonable to hypothesize that the streamwise wall-shear stress fluctuation
$C_2=0.00629$. Only minor discrepancies between DNS data and model predictions can be observed. As such, it is reasonable to hypothesize that the streamwise wall-shear stress fluctuation ![]() $\tau '_x$ generated by attached eddies of a given size follows the Gaussian distribution. Moreover, we can also estimate the statistical moments of
$\tau '_x$ generated by attached eddies of a given size follows the Gaussian distribution. Moreover, we can also estimate the statistical moments of ![]() $\tau _{x,o}^{+}$ by taking the derivative of
$\tau _{x,o}^{+}$ by taking the derivative of ![]() $G(q,y_e^+)$ with respect to
$G(q,y_e^+)$ with respect to ![]() $q$ around
$q$ around ![]() $q=0$ (Yang et al. Reference Yang, Marusic and Meneveau2016), i.e.
$q=0$ (Yang et al. Reference Yang, Marusic and Meneveau2016), i.e.
 \begin{gather} \left\langle \tau_{x,o}^{'4+} \right\rangle^{1/2}=\left(\left.\frac{\partial^{4} G(q ;y_o^+)}{\partial q^{4}}\right|_{q=0}\right)^{1/2} \sim 2\sqrt{3}C_2\ln(y_o/y_s) \sim 2\sqrt{3}C_2\ln Re_{\tau}, \end{gather}
\begin{gather} \left\langle \tau_{x,o}^{'4+} \right\rangle^{1/2}=\left(\left.\frac{\partial^{4} G(q ;y_o^+)}{\partial q^{4}}\right|_{q=0}\right)^{1/2} \sim 2\sqrt{3}C_2\ln(y_o/y_s) \sim 2\sqrt{3}C_2\ln Re_{\tau}, \end{gather} \begin{gather} \left\langle \tau_{x,o}^{'6+} \right\rangle^{1/3} =\left(\left.\frac{\partial^{6} G(q ;y_o^+)}{\partial q^{6}}\right|_{q=0}\right)^{1/3} \sim 2\sqrt[3]{15}C_2\ln(y_o/y_s) \sim 2\sqrt[3]{15}C_2\ln Re_{\tau}. \end{gather}
\begin{gather} \left\langle \tau_{x,o}^{'6+} \right\rangle^{1/3} =\left(\left.\frac{\partial^{6} G(q ;y_o^+)}{\partial q^{6}}\right|_{q=0}\right)^{1/3} \sim 2\sqrt[3]{15}C_2\ln(y_o/y_s) \sim 2\sqrt[3]{15}C_2\ln Re_{\tau}. \end{gather} Figure 3(b) shows the variations of second- (![]() $p=1$) to sixth- (
$p=1$) to sixth- (![]() $p=3$) order moments of
$p=3$) order moments of ![]() $\tau '_x$ calculated from DNS of channel flows (Iwamoto, Suzuki & Kasagi Reference Iwamoto, Suzuki and Kasagi2002; Del Álamo & Jiménez Reference Del Álamo and Jiménez2003; Abe et al. Reference Abe, Kawamura and Choi2004; Del Álamo et al. Reference Del Álamo, Jiménez, Zandonade and Moser2004; Hu, Morfey & Sandham Reference Hu, Morfey and Sandham2006; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014; Lee & Moser Reference Lee and Moser2015; Cheng et al. Reference Cheng, Li, Lozano-Durán and Liu2019; Kaneda & Yamamoto Reference Kaneda and Yamamoto2021) and compares them with the model prediction, i.e. (4.2)–(4.4). For the second- and fourth-order variances, the model predictions are roughly consistent with the DNS results. The comparisons also indicate a Reynolds-number dependence of
$\tau '_x$ calculated from DNS of channel flows (Iwamoto, Suzuki & Kasagi Reference Iwamoto, Suzuki and Kasagi2002; Del Álamo & Jiménez Reference Del Álamo and Jiménez2003; Abe et al. Reference Abe, Kawamura and Choi2004; Del Álamo et al. Reference Del Álamo, Jiménez, Zandonade and Moser2004; Hu, Morfey & Sandham Reference Hu, Morfey and Sandham2006; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014; Lee & Moser Reference Lee and Moser2015; Cheng et al. Reference Cheng, Li, Lozano-Durán and Liu2019; Kaneda & Yamamoto Reference Kaneda and Yamamoto2021) and compares them with the model prediction, i.e. (4.2)–(4.4). For the second- and fourth-order variances, the model predictions are roughly consistent with the DNS results. The comparisons also indicate a Reynolds-number dependence of ![]() $\langle \tau _{x}^{'2+} \rangle$, which has been reported by vast studies (Schlatter & Örlü Reference Schlatter and Örlü2010; Mathis et al. Reference Mathis, Marusic, Chernyshenko and Hutchins2013; Guerrero et al. Reference Guerrero, Lambert and Chin2020), and may be ascribed to the superposition effects of the wall-attached log-region motions. Wang, Pan & Wang (Reference Wang, Pan and Wang2020) speculated that the amplitude modulation effect plays a more prominent role in affecting the statistic characteristics of
$\langle \tau _{x}^{'2+} \rangle$, which has been reported by vast studies (Schlatter & Örlü Reference Schlatter and Örlü2010; Mathis et al. Reference Mathis, Marusic, Chernyshenko and Hutchins2013; Guerrero et al. Reference Guerrero, Lambert and Chin2020), and may be ascribed to the superposition effects of the wall-attached log-region motions. Wang, Pan & Wang (Reference Wang, Pan and Wang2020) speculated that the amplitude modulation effect plays a more prominent role in affecting the statistic characteristics of ![]() $\tau _{x,rms}^{'+}$ than the superposition effect, which contradicts the present findings. In fact, amplitude modulation has been demonstrated to exert a negligible effect on the even-order moments (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011; Blackman, Perret & Mathis Reference Blackman, Perret and Mathis2019). Therefore, the deduction of Wang et al. (Reference Wang, Pan and Wang2020) needs to be revisited. For sixth-order moments, the model prediction displays substantial discrepancies with the DNS data. It is expected since high-order moments are dominated by the rare events resulting from the intermittent small-scale motions (Frisch & Donnelly Reference Frisch and Donnelly1996), which cannot be captured by the IOIM (see figure 5a).
$\tau _{x,rms}^{'+}$ than the superposition effect, which contradicts the present findings. In fact, amplitude modulation has been demonstrated to exert a negligible effect on the even-order moments (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011; Blackman, Perret & Mathis Reference Blackman, Perret and Mathis2019). Therefore, the deduction of Wang et al. (Reference Wang, Pan and Wang2020) needs to be revisited. For sixth-order moments, the model prediction displays substantial discrepancies with the DNS data. It is expected since high-order moments are dominated by the rare events resulting from the intermittent small-scale motions (Frisch & Donnelly Reference Frisch and Donnelly1996), which cannot be captured by the IOIM (see figure 5a).
The ESS (i.e. (2.6)) is another scaling predicted by the multifractal formalism. Different from SSS, ESS does not rely on the identically and independently distribution of the addends, but the additive process (see (2.2)). Figures 4(a) and 4(b) shows the ESS scalings for ![]() $q_0=-2$ and
$q_0=-2$ and ![]() $q_0=2$, respectively. The ESS holds for the entire logarithmic region. The observation suggests that the streamwise wall-shear fluctuations generated by logarithmic motions obey the additive process, though the streamwise wall-shear fluctuations generated by attached eddies with wall-normal heights at approximately
$q_0=2$, respectively. The ESS holds for the entire logarithmic region. The observation suggests that the streamwise wall-shear fluctuations generated by logarithmic motions obey the additive process, though the streamwise wall-shear fluctuations generated by attached eddies with wall-normal heights at approximately ![]() $0.2h^+$ are not i.i.d. due to the scale interactions (see figure 2), which are not described by the attached-eddy model.
$0.2h^+$ are not i.i.d. due to the scale interactions (see figure 2), which are not described by the attached-eddy model.

Figure 4. (a) ![]() $G(q)$ as functions of
$G(q)$ as functions of ![]() $G(-2)$ for
$G(-2)$ for ![]() $q=-1,-3,-5,-7$; (b)
$q=-1,-3,-5,-7$; (b) ![]() $G(q)$ as functions of
$G(q)$ as functions of ![]() $G(2)$ for
$G(2)$ for ![]() $q=1,3,5,7$. Both vertical and horizontal axes in (a,b) are plotted in logarithmic form.
$q=1,3,5,7$. Both vertical and horizontal axes in (a,b) are plotted in logarithmic form.
4.2. Instantaneous distribution of  $\tau '_x$
$\tau '_x$
Furthermore, the instantaneous ![]() $\tau _x^{'+}$ can be decomposed as
$\tau _x^{'+}$ can be decomposed as
 \begin{equation} \tau_x^{'+}=\tau_{x,s}^{'+}+\underbrace{\tau_{x,L}^{'+}(y_s^+)-\tau_{x,L}^{'+}(y_e^+)}_{\tau_{x,log}^{'+}}+\underbrace{\tau_{x,L}^{'+}(y_e^+)}_{\tau_{x,out}^{'+}}, \end{equation}
\begin{equation} \tau_x^{'+}=\tau_{x,s}^{'+}+\underbrace{\tau_{x,L}^{'+}(y_s^+)-\tau_{x,L}^{'+}(y_e^+)}_{\tau_{x,log}^{'+}}+\underbrace{\tau_{x,L}^{'+}(y_e^+)}_{\tau_{x,out}^{'+}}, \end{equation}
where ![]() $\tau _{x,s}^{'+}$ denotes the amplitude modulation of the universal signal
$\tau _{x,s}^{'+}$ denotes the amplitude modulation of the universal signal ![]() $\tau _{x}^{'*+}$;
$\tau _{x}^{'*+}$; ![]() $\tau _{x,log}^{'+}$ and
$\tau _{x,log}^{'+}$ and ![]() $\tau _{x,out}^{'+}$ are the superposition components contributed from the log region and the outer wall-coherent motions, respectively. The methodology of removing modulation effects can be found in Mathis et al. (Reference Mathis, Hutchins and Marusic2011) and Baars et al. (Reference Baars, Hutchins and Marusic2016), whose details are out of the range of the present study. Figure 5(a) shows the probability density functions (p.d.f.s) of
$\tau _{x,out}^{'+}$ are the superposition components contributed from the log region and the outer wall-coherent motions, respectively. The methodology of removing modulation effects can be found in Mathis et al. (Reference Mathis, Hutchins and Marusic2011) and Baars et al. (Reference Baars, Hutchins and Marusic2016), whose details are out of the range of the present study. Figure 5(a) shows the probability density functions (p.d.f.s) of ![]() $\tau _{x}^{'*+}$,
$\tau _{x}^{'*+}$, ![]() $\tau _{x,s}^{'+}$,
$\tau _{x,s}^{'+}$, ![]() $\tau _{x,log}^{'+}$ and
$\tau _{x,log}^{'+}$ and ![]() $\tau _{x,out}^{'+}$, and compares with the p.d.f. for the full channel data. The p.d.f.s of
$\tau _{x,out}^{'+}$, and compares with the p.d.f. for the full channel data. The p.d.f.s of ![]() $\tau _{x,s}^{'+}$ and
$\tau _{x,s}^{'+}$ and ![]() $\tau _{x}^{'*+}$ nearly coincide with that of
$\tau _{x}^{'*+}$ nearly coincide with that of ![]() $\tau _{x}^{'+}$ with asymmetric and positively skewed shape, which demonstrates that removing the superposition and modulation effects barely affects the instantaneous distributions. The asymmetries between the positive and negative wall-shear fluctuations are the essential characters of the near-wall small-scale turbulence, which may be associated with the celebrated near-wall sustaining process (Schoppa & Hussain Reference Schoppa and Hussain2002). In contrast, the p.d.f.s of
$\tau _{x}^{'+}$ with asymmetric and positively skewed shape, which demonstrates that removing the superposition and modulation effects barely affects the instantaneous distributions. The asymmetries between the positive and negative wall-shear fluctuations are the essential characters of the near-wall small-scale turbulence, which may be associated with the celebrated near-wall sustaining process (Schoppa & Hussain Reference Schoppa and Hussain2002). In contrast, the p.d.f.s of ![]() $\tau _{x,log}^{'+}$ and
$\tau _{x,log}^{'+}$ and ![]() $\tau _{x,out}^{'+}$ are more symmetric with rare events invisible, suggesting that the superposition components of logarithmic and outer motions are less intermittent than the small-scale universal signals. This also explains the reason why the log-normal model describes the additive process well (see figure 3a), although the log-normal model is inapplicable for rare events (Landau & Lifshitz Reference Landau and Lifshitz1987). Moreover, the skewness and flatness of
$\tau _{x,out}^{'+}$ are more symmetric with rare events invisible, suggesting that the superposition components of logarithmic and outer motions are less intermittent than the small-scale universal signals. This also explains the reason why the log-normal model describes the additive process well (see figure 3a), although the log-normal model is inapplicable for rare events (Landau & Lifshitz Reference Landau and Lifshitz1987). Moreover, the skewness and flatness of ![]() $\tau _{x,log}^{'+}$ are 0.05 and 2.91, which are very close to those of a Gaussian distribution. It strongly supports the conclusion drawn above that the streamwise wall-shear stress fluctuations generated by attached eddies populating the logarithmic region can be absolutely treated as Gaussian variables with
$\tau _{x,log}^{'+}$ are 0.05 and 2.91, which are very close to those of a Gaussian distribution. It strongly supports the conclusion drawn above that the streamwise wall-shear stress fluctuations generated by attached eddies populating the logarithmic region can be absolutely treated as Gaussian variables with
where ![]() $p(\xi )$ denotes the p.d.f., and
$p(\xi )$ denotes the p.d.f., and ![]() $\xi$ is the independent variable. It is worth noting that the variation of variance can be well predicted by the log-normal model, namely,
$\xi$ is the independent variable. It is worth noting that the variation of variance can be well predicted by the log-normal model, namely,
where ![]() $C_2\approx 0.00629$, and
$C_2\approx 0.00629$, and ![]() $C_3\approx -0.07959$ is a constant and determined by the DNS data at
$C_3\approx -0.07959$ is a constant and determined by the DNS data at ![]() $Re_{\tau }=2003$. Figure 5(b) shows the p.d.f.s of
$Re_{\tau }=2003$. Figure 5(b) shows the p.d.f.s of ![]() $\tau _{x,log}^{'+}$ and the model prediction by (4.6), results of two other Reynolds numbers (Del Álamo et al. Reference Del Álamo, Jiménez, Zandonade and Moser2004; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014) are also included for comparison. It can be seen that the Gaussian model proposed here works reasonably well and can cover a wide range of Reynolds numbers. The model remains to be validated by higher-Reynolds-number DNS data.
$\tau _{x,log}^{'+}$ and the model prediction by (4.6), results of two other Reynolds numbers (Del Álamo et al. Reference Del Álamo, Jiménez, Zandonade and Moser2004; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014) are also included for comparison. It can be seen that the Gaussian model proposed here works reasonably well and can cover a wide range of Reynolds numbers. The model remains to be validated by higher-Reynolds-number DNS data.

Figure 5. (a) The p.d.f.s of ![]() $\tau _{x}^{'*+}$,
$\tau _{x}^{'*+}$, ![]() $\tau _{x,s}^{'+}$,
$\tau _{x,s}^{'+}$, ![]() $\tau _{x,log}^{'+}$,
$\tau _{x,log}^{'+}$, ![]() $\tau _{x,out}^{'+}$, and
$\tau _{x,out}^{'+}$, and ![]() $\tau _{x}^{'+}$; (b) The p.d.f.s of
$\tau _{x}^{'+}$; (b) The p.d.f.s of ![]() $\tau _{x,log}^{'+}$ in channel flows with
$\tau _{x,log}^{'+}$ in channel flows with ![]() $Re_{\tau }=934$,
$Re_{\tau }=934$, ![]() $2003$, and
$2003$, and ![]() $4179$. Dashed lines denote the Gaussian model predictions with (4.6)–(4.7).
$4179$. Dashed lines denote the Gaussian model predictions with (4.6)–(4.7).
5. Concluding remarks
In summary, the present study reveals that the IOIM and the AEM are consistent with each other quantitatively. The statistical characteristics of the superpositions of log-region eddies follow the predictions of the AEM, namely, the SSS and ESS scalings. Based on these observations, we conclude that the streamwise wall-shear stress fluctuations generated by attached eddies populating the logarithmic region can be treated as Gaussian variables. A Gaussian model is then proposed to describe their instantaneous distributions and verified by DNS data spanned broad-band Reynolds numbers. Considering the fact that the intensity of wall-shear stress fluctuations is typically underpredicted by state-of-the-art wall-modelled large-eddy simulation (WMLES) approaches (Park & Moin Reference Park and Moin2016), the Gaussian model proposed in the present study may be constructive for the development of the LES methodology, and the distribution characteristics of ![]() $\tau _{x}^{'*+}$ are helpful for developing more accurate near-wall models of WMLES approaches.
$\tau _{x}^{'*+}$ are helpful for developing more accurate near-wall models of WMLES approaches.
It is noted that some previous works adopted the IOIM to investigate the spectral characteristics of the wall-coherent components of the signals in the near-wall region, such as the work of Marusic, Baars & Hutchins (Reference Marusic, Baars and Hutchins2017), but whether they are consistent with the AEM predictions in physical space quantitatively has not been verified in detail. The consistency of the two models demonstrated here fills the gap and complements their works. Moreover, the findings in the present study indicate that we can isolate the footprints of attached eddies within a selected wall-normal range by employing the IOIM, i.e. by adjusting ![]() $y_1^+$ and
$y_1^+$ and ![]() $y_2^+$ in
$y_2^+$ in ![]() $\tau _{x,L}^{'+}(y_1^+)-\tau _{x,L}^{'+}(y_2^+)$. Here,
$\tau _{x,L}^{'+}(y_1^+)-\tau _{x,L}^{'+}(y_2^+)$. Here, ![]() $y_1^+$ and
$y_1^+$ and ![]() $y_2^+$ are two selected wall-normal heights in the logarithmic region, and
$y_2^+$ are two selected wall-normal heights in the logarithmic region, and ![]() $y_1^+< y_2^+$. In this regard, the present study may provide a new perspective for analysing some flow physics in wall-bounded turbulence, such as the inner peak of the intensity of
$y_1^+< y_2^+$. In this regard, the present study may provide a new perspective for analysing some flow physics in wall-bounded turbulence, such as the inner peak of the intensity of ![]() $u'$, and the streamwise inclined angles of attached eddies. All these are under investigation currently and will be reported in separate forthcoming papers.
$u'$, and the streamwise inclined angles of attached eddies. All these are under investigation currently and will be reported in separate forthcoming papers.
Acknowledgements
We are grateful to the authors cited in figure 3(b) for making their invaluable data available.
Funding
L.F. acknowledges the fund from CORE as a joint research centre for ocean research between QNLM and HKUST.
Declaration of interests
The authors report no conflict of interest.