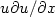Barriers of very different character such as localized obstacles and the extended Peierls- Nabarro relief may control the dislocation motion in crystals in different stress and temperature ranges. The great difference in the microscopic parameters characterizing these two mechanisms, e.g., in the activation volumes, manifests itself even on the macroscopic scale as a strong change of the plastic properties in a rather narrow transition range of the temperature. A theory describing the temperature dependence of the flow stress and the strain rate sensitivity near the transition has been developed and compared with experimental data on the plastic deformation of cubic ZrO2 single crystals in a soft orientation.

We have studied Zr1−XCeXO2 film growth on (001) Si by Pulsed Laser Deposition using sputtering of metallic alloy targets and sintered ceramic targets. The conditions of the epitaxial growth have been found and optimized. The epitaxial oxide film growth (001) [100]||(001) [100] Si was obtained for a range of CeO2 content in ZrO2: from 4.5 up to 14% mol in ZrO2. The oxide film structure corresponds to a tetragonal phase with strong preference for c-axis orientation normal to the growth surface. The results obtained by RHEED, XRD and AFM methods have confirmed the high quality of heteroepitaxial Zr1−XCeXO2 layers, and the difference in crystallinities for the films grown from metallic alloy targets and ceramic targets was evaluated. The XRD results show the absence of any reflection distinct from (00l) and (l00) for films grown from alloy targets, and, in contrast with this, the film structure contains some random oriented inclusions in the case of oxide target deposition. Use of metallic alloy Zr-12% Ce targets and low oxygen pressure during deposition provide the best film quality with the minimum of surface microrelief (Rrms < 0.3 nm for 1 × 1 µm2 surface area was achieved).

The optical properties of Ag-TiO2 nanocermet thin films are studied with the aim of optical filtering applications. Beyond the classical properties of cermets with noble metal inclusions predicted by the effective medium theories, the optical properties of Ag-TiO2 nanocermets deposited by R.F. co-sputtering are governed by their columnar morphology and the under-stoichiometry of the TiO2 matrix. A careful experimental analysis of the different parameters and effects involved in the optical response of these nanocermets is performed both on TiO2 and Ag-TiO2: film thickness, silver volume fraction, thermal treatments, oxidation. The influence of these parameters on the surface plasmon resonance and the infrared transmission of the nanocermet thin films is optimized.

Heterogeneous CoxAg1−x and NixAg1−x alloys have giant magnetoresistance properties. Such alloys, with atomic concentrations x = 0.20 and 0.37, were studied by transmission X-ray Absorption Spectroscopy at the Co or Ni K-edge after in situ thermal annealing. For alloys as-deposited and annealed at 200 °C, Extended X-ray Absorption Fine Structure analysis displays both Co-Co (Ni-Ni) bonds related to Co (Ni) atoms agglomerated in magnetic particles and Co-Ag (Ni-Ag) bonds related to Co (Ni) atoms in substitutional sites in the Ag matrix. At the same alloy concentration, the miscibility in the Ag matrix is found larger for Ni than for Co. After annealing around 250 °C, the marked decrease of the Ag neighbour peak corresponds to a diffusion of magnetic atoms outside the Ag matrix. The Co-Co coordination number increases regularly with annealing temperatures up to 450 °C reflecting a progressive expansion of Co particles. On the contrary, for Ni alloys, no further particle expansion has been observed in the same annealing range. This different behaviour may be linked both to the difference between the as-deposited structural states and to the Co/Ag and Ni/Ag interfaces energies. Using a simple model, evolution of the mean particle size has been estimated as a function of annealing.

Granular Fe-V2O5 thin films with different iron concentrations prepared by means of radiofrequency magnetron co-sputtering technique were investigated by means of X-ray diffraction, Transmission Electron Microscopy and 57Fe Mössbauer spectrometry as a function of iron concentration. A common experimental feature reveals that a percolation-like threshold occurs at around 23−25% atomic Fe. Below such a critical value, the co-sputtering process favours the presence of ultrafine amorphous oxide grains with sizes lower than 10 nm embedded in a vanadium oxide matrix. Above, one clearly observes the presence of fine grains (sizes comprised between 10−100 nm) composed of either hematite or maghemite phases dispersed in the same matrix, the set displaying a magnetic order at room temperature.

I-V-T data is routinely used to determine the conduction band discontinuity in heterojunction structures. In the present paper, capacitance-voltage and current-voltage-temperature measurements performed on AlGaAs/GaAs isotype heterojunctions are presented and analysed over a wide temperature range (77 K-300 K). Considering thermionic emission alone when analysing I-V-T data resulted in several problems. The Richardson plot $[\ln(J_0/T^2) vs. 1/T]$, in particular while suggesting that the thermally activated process is of importance in the overall conduction mechanism, shows two distinct linear regions of different slope over two temperature ranges. Also the derived activation energies and hence the band discontinuity from I-V-T data is very much lower than the value obtained from C-V profiling which is in very good agreement with values routinely published in literature. However, the results obtained from both I-V-T and C-V data are reconciled when considering a simple analytical expression for the current based on the assumption that thermally assisted tunneling is the dominant current generating mechanism over most of the temperature range.

The microcrack distribution in a low porous granite exposed to weathering after quarrying was investigated in order to detect its microstructural evolution. Two blocks (A and B) were taken in the same granite body from two quarry faces respectively exposed during a few weeks and twenty years. Porosimetry by injection of carbon-14-methylmethacrylate (14C-MMA) was used for analysing the porous medium. Measurements of optical densities of autoradiographs provided data for the localization and the quantification of porosity. Results are compared with those obtained by mercury porosimetry. Average porosity of sample A was found to be 0.37 ± 0.03% whereas average porosity in sample B reaches 1.07 ± 0.45%. Most of the porosity increase may be explained by the opening of grain boundaries.

EELS (electron energy loss spectrometry) in the transmission electron microscope (TEM) was used to determine the composition of a nanocrystalline magnetic specimen. The relative amounts of the hard magnetic phase Nd2Fe14B and the soft magnetic phase Fe3B at the point of measurement was measured by standard EELS quantification. In order to determine the structure of Fe3B present, the fine structure of the boron K-ionisation edge was analysed. Comparison of the experimental spectra with simulations of the fine structures based on the TELNES extension of the WIEN97 program package, a full potential linearised augmented plane wave approach to the calculation of electronic structure in crystals, shows that the tetragonal form of Fe3B is predominant.

Our purpose is to build an inverse method which best fits a model of artery flow and experimental measurements (we assume that we are able to measure the displacement of the artery as a function of time at three stations). Having no clinical data, we simulate these measurements with the numerical computations from a "boundary layer" code. First, we revisit the system of Ling and Atabek of boundary layer type for the transmission of a pressure pulse in the arterial system for the case of an elastic wall (but we solve it without any simplification in the $u\partial u/\partial x$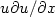 term). Then, using a method analogous to the well known Von Kármán-Pohlhausen method from aeronautics but transposed here for a pulsatile flow, we build a system of three coupled non-linear partial differential equations depending only on time and axial co-ordinate. This system governs the dynamics of internal artery radius, centre velocity and a quantity related to the presence of viscous effects. These two methods give nearly the same numerical results. Second, we construct an inverse method: the aim is to find for the simple integral model, the physical parameters to put in the "boundary layer" code (simulating clinical data). This is done by varying in the integral model the viscosity and elasticity in order to fit best with the data. To achieve this in a rational way, we have to minimise a cost function, which involves the computation of the adjoint system of the integral method. The good set of parameters (i.e. viscosity, and two coefficients of a wall law) is effectively found again. It opens the perspective for application in real clinical cases of this new non-invasive method for evaluating the viscosity of the flow and elasticity of the wall.

This paper mainly deals with the design of an advanced control law for induction motors and its real-time implementation on an experimental test benchmark. First, relationship between the classical field oriented control (FOC) and non linear linearizing control laws is studied. It is shown that both control laws are similar. Classical non linear linearizing control improves the performances but not in a spectacular way when the observer and the controller are designed independently. A new non linear observer based control law is designed, which is shown to be globally stable and is implemented on an experimental test-bench. The control algorithm is studied and applied in many configurations (various set-points, flux and speed profiles and torque disturbances) and is shown to be very efficient.