1. Introduction
Inspired by nature, soft robotics offer unique opportunities to develop autonomous systems that can provide multi-functional features, structural flexibility, and more degrees of freedom than traditional robotics. While the foregoing attributes are highly desirable, they pose various challenges that limit their implementation in realistic situations. Particularly in the area of dielectric elastomer (DE) transducers, which have found many applications [Reference Anderson, Gisby, McKay, O’Brien and Calius1–Reference Cao, Gao and Conn15], some of these challenges can be related to the diversity of behaviors exhibited by typical DE materials, depending on loading and environmental conditions, at least. Modeling challenges stem from the dynamic and complex microstructures of polymeric materials and their effects on the electromechanical behavior during operation (see Fig. 1). Besides stretch state-dependent electrical properties, DEs exhibit mechanical behaviors with dependence on both strain rate and temperature. Also, they can display hysteresis, strain-softening, and strain-hardening behaviors during cycling loading [Reference Khajehsaeid, Arghavani, Naghdabadi and Sohrabpour16, Reference Amin, Lion, Sekita and Okui17], see Fig. 1. These combined effects call out for more careful modeling and model implementations, especially in realistic configurations that depart from lab-based schemes [Reference Dorfmann and Ogden18–Reference Grasinger and Dayal22]. In fact, the aforementioned complexities have recently motivated researchers to explore data-driven algorithms such as reinforcement learning to model DE material behavior [Reference Yang, Xiao, Zhang, Liang, Li, Zhang, Li, Wong, Wang, Li and Huang23, Reference Massenio, Rizzello, Comitangelo, Naso and Seelecke24]. However, this type of modeling scheme is in its infancy stage and physics-based material modeling is still the de facto method in the research/development community. In order to alleviate some of the modeling challenges, researchers and developers assume simplified models such as constant electrical properties. Unfortunately, these assumptions can become critical in certain applications requiring a large range of deformations [Reference Kumar and Patra25, Reference Su, Wu, Chen and Lü26] or high accuracy requirements.
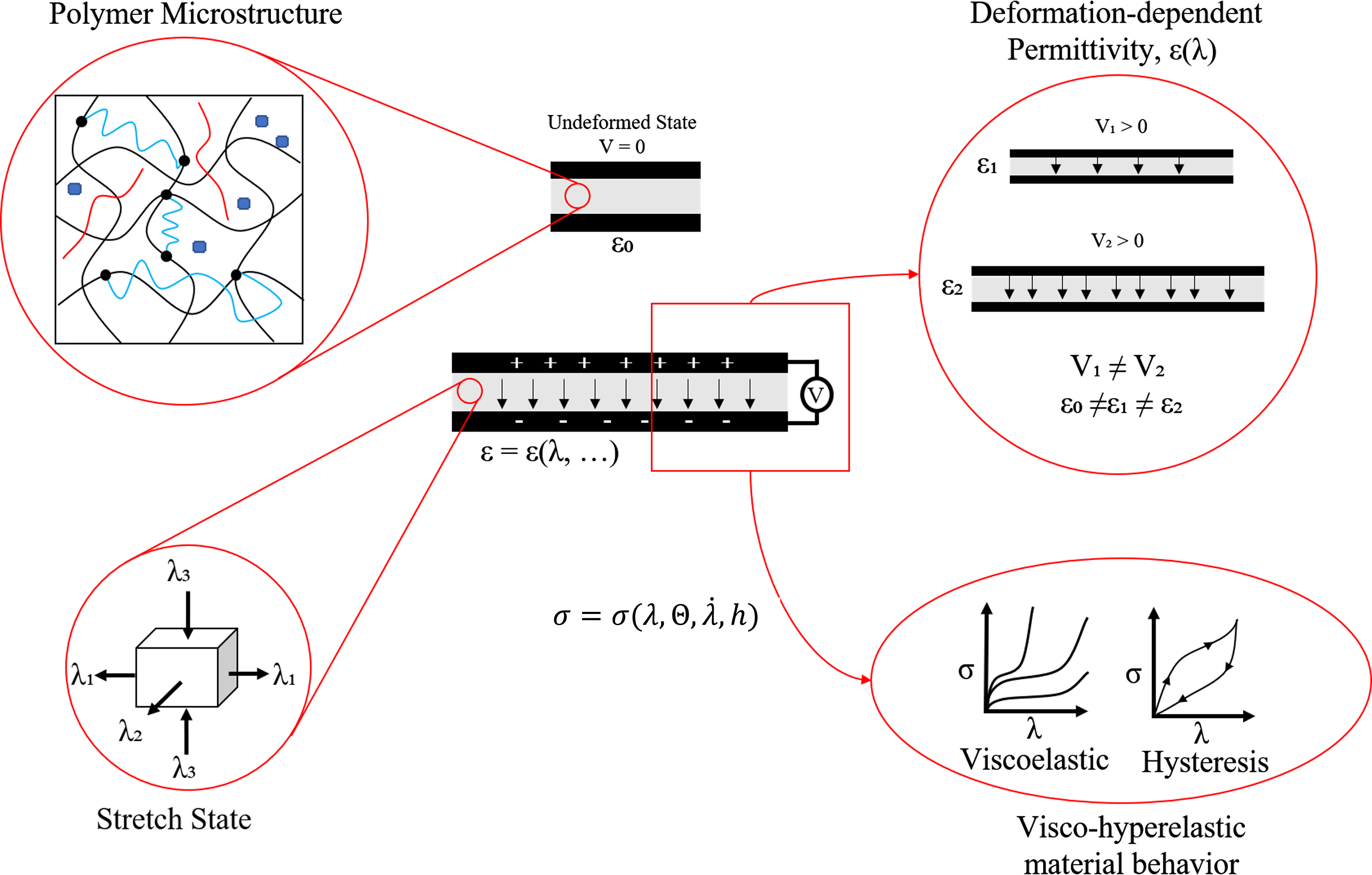
Figure 1. A dielectric elastomer membrane is typically a polymeric material with highly complex molecular structure: crosslinking, entanglement, sliplinks, impurities, etc. The membrane can be actuated by the application of electrical potential (V). This causes the material to deform with principal stretches (
$\lambda _1$
,
$\lambda _2$
,
$\lambda _3$
). The stress (
$\sigma$
) induced is a function not only of stretch but also of temperature (
$\Theta$
), strain rate (
$\dot{\lambda }$
), and humidity (h). Electrically, the permittivity of the material changes with stretch due to the rearrangement of the molecular structure. This state of affairs renders the material highly nonlinear, viscoelastic and hysteric, and thus difficult to be universally modeled.
As perused in the literature, the deformation dependency of electrical properties (e.g. permittivity) of DEs has rarely been implemented in actual soft robotic applications. Instead, as implied above, many reported works were based on constant permittivity [Reference Zhu, Cai and Suo27–Reference Medina and Farmer33]. This has been a long-standing assumption since it was shown that for a commonly used DE material, VHB 4910, the change in dielectric constant is less than 5% for a radial stretch of five [Reference Kofod, Sommer-Larsen, Kornbluh and Pelrine34]. Using that assumption and the idea of ignoring the effects of crosslinks in polarization, Suo [Reference Suo35] presented, what he called, an ideal DE where the polarization is equivalent to that of a polymer melt. Hence, one of the tenets of this ideal DE is constant permittivity. This allows for the easy relation between the true electric field,
$E$
, and true electric displacement,
$D$
, such that,
$ E=\frac{D}{\varepsilon _0}$
, where
$\varepsilon _0$
is the constant dielectric permittivity in any direction. Interestingly, there seems to be some discrepancies related to reported values of
$\varepsilon _0$
. This can be noted from the wide range of values used for VHB 4910, for example.Footnote
1
Qiang et al. also reported changes in permittivity of unstretched VHB 4910 due to both frequency and temperature [Reference Qiang, Chen and Li40]. McKay et al. investigated this wide range of results and reported that the dielectric permittivity “is highly sensitive to the characterization technique” [Reference McKay, Calius and Anderson41]. This leads to the conclusion that more factors should be taken into account when reporting the dielectric constant of a material, and assuming a constant permittivity is not always a valid assumption.
It has been shown that, in fact, the electrical permittivity can exhibit a highly nonlinear dependency on stretch [Reference Kumar and Patra25, Reference Jiménez and McMeeking42–Reference Tagarielli, Hildick-Smith and Huber50]. Furthermore, under certain conditions, deformation-dependent permittivity can reveal material instabilities and/or potential dielectric breakdowns [Reference Jiménez and McMeeking42, Reference Gei, Colonnelli and Springhetti51–Reference Li, Chen, Zhao and Yang53]. This is partly due to the intricate electromechanical properties exhibited by DEs that are rooted on their labyrinthine polymeric (or nanocomposite) microstructure. Based on the pioneering work by Kuhn and Grün [Reference Kuhn and Grün54], some authors have proposed deformation-dependent permittivity models [Reference Cohen and deBotton20, Reference Jiménez and McMeeking42–Reference Tröls, Kogler, Baumgartner, Kaltseis, Keplinger, Schwödiauer, Graz and Bauer46, Reference Jiménez and McMeeking55]. Others have attempted to accomplish this by empirical means [Reference Dorfmann and Ogden18, Reference Kumar and Patra25, Reference Sheng, Chen, Li and Wang56, Reference Schlögl and Leyendecker57]. The implementation of such models has been limited, however, to uniaxially or biaxially loaded planar DE actuators (DEAs), and hence their utilization on more complex (or realistic) configurations is lacking. For example, a particular configuration that has found many applications in soft robotics is the family of the so-called conical DEAs (CDEAs) [Reference Cao, Gao and Conn15, Reference Korn, Farmer and Medina58–Reference Zhang, Lai, Rao, Zhang and Yurchenko61]. These CDEAs can be used for multiple applications being that they can exhibit motion with large ranges, high prescribability, smoothness, reasonable bandwidth of
$\mathcal{O}(10^0)$
to
$\mathcal{O}(10^3)$
Hz, and capability of resonance. Due to their broad potential, their employment is pursued by both experts and non-experts in the field of soft robotics [Reference Cao, Gao and Conn15, Reference Berselli, Vertechy, Vassura and Parenti-Castelli30, Reference Cao and Conn31, Reference Linnebach, Rizzello and Seelecke59, Reference Ye, Chen, Asmatulu and Chan60, Reference Dubowsky, Kesner, Plante and Boston62, Reference Bortot and Gei63]. In none of those aforecited works, the electrical properties of the DE were assumed to vary with stretch state. However, in cases of inhomogeneous deformation, as typically observed in single-cone DEA (SCDEA) [Reference Korn, Farmer and Medina58] or double conical DEA [Reference Medina and Farmer33, Reference Farmer and Medina64], the permittivity is expected to vary throughout the membrane. For applications that rely on those configurations, such as knee joints [Reference Zhao, Niu, McCoul, Ren and Pei7, Reference Nguyen, Phung, Nguyen, Jung and Choi8], pumps [Reference Christianson, Goldberg and Tolley14, Reference Cao, Gao and Conn15, Reference Linnebach, Rizzello and Seelecke59], and pulse tracking devices [Reference Ye, Chen, Asmatulu and Chan60], a model that accurately describes the inhomogeneities experienced by the membrane is required for highly precise control and sensing. In addition, for implementation of models in finite element analysis (or the like), more robust modeling schemes would enhance local (mesh level) accuracy. As far the authors know, there has not been any modeling work for CDEAs that include stretch-dependent permittivity.
Therefore, in the current work, we present a study of the out-of-plane deformation (OPD) of a SCDEA using a constitutive stretch-dependent permittivity model. Furthermore, our work utilizes a hyperelastic model that accounts for the effects of entanglement and sliplinks of the polymer network. Even though our base configuration is described as a conical actuator, our analysis and conclusions are extended to DE-based sensors. A direct example application would be a self-sensing CDEA for a soft robotic limb to create a feedback loop for sensing and controlling the displacement.
This article starts by presenting a brief compilation of the stretch-dependent permittivity models, followed by the equations of state for describing the deformation of a SCDEA. Afterwards, we combine our selected mechanical and electrical models to investigate the OPD of the SCDEA. Discussions are presented that reveal certain bifurcation behaviors due to the electromechanical coupling of hyperelasticity with stretch-dependent permittivity, applicable to both actuators and sensors. The deformation-dependent permittivity results and discussion can be viewed as a theoretical study of material properties at the limit.
2. Electrical and hyperelastic material models
In the sequel, a brief survey of the permittivity-varying models is presented. Emphasis is placed on a particular constitutive model, which is later employed in this work. In addition, six commonly used hyperelastic material modelsFootnote 2 are used in a later comparison using the OPD of a SDCEA configuration. Ultimately, a hyperelastic model that considers the effects of entanglements and sliplinks in the polymer network is selected and later employed. A detailed description of the hyperelastic models considered can be found in Appendix A.
2.1. Deformation-dependent permittivity models
The electrical properties of DEs can be highly nonlinearly dependent on the stretch state, see Fig. 2. Table I provides a summary of a selection of the reported literature on such models.Footnote 3 Some of the models reported can be classified as constitutive in that they were developed from: either (a) statistical mechanics principles based on the polymer networks, (b) continuum mechanics principles, or (c) a simplified expression of the previous two. The empirical models borrowed the invariant-based-polynomial approach typical of some hyperelastic modeling scheme (such as Yeoh or Ogden). The interested reader is invited to peruse the provided literature in Table I for more details.
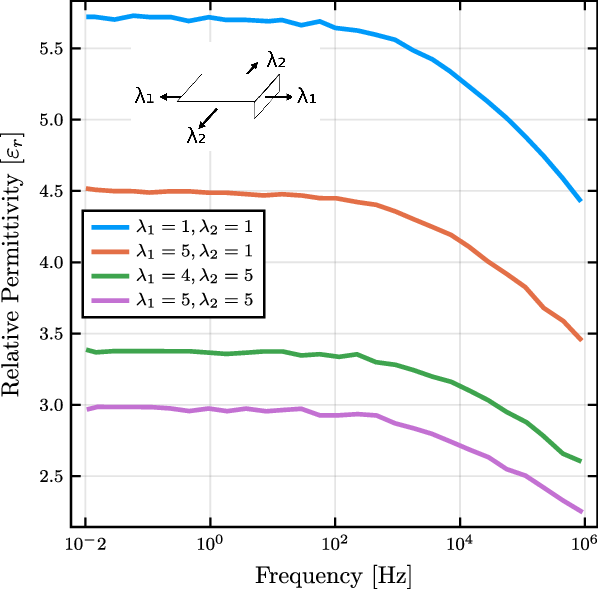
Figure 2. From biaxial stretch states, the relative permittivity of VHB4910 exhibits a deformation dependence for across a range of alternating-current (AC) frequencies. Recreated from ref. [Reference Kumar and Patra25].
Table I. A brief summary of works (or models) that consider deformation -dependent permittivity.
Theoretical pioneering work developed by Kuhn and Grün [Reference Kuhn and Grün54] predicted that both electrical and optical properties of some elastomers are dependent on the deformation state. Several experimental studiesFootnote
4
have shown that the dielectric permittivity is highly dependent on the deformation (or stress) of the DE membrane [Reference Di Lillo, Schmidt, Carnelli, Ermanni, Kovacs, Mazza and Bergamini43–Reference Cohen, Oren and deBotton49]. Following the framework outlined by Kuhn and Grün [Reference Kuhn and Grün54], Jimenèz et al. developed an analytical solution for determining the dielectric permittivity provided the stretch state is known [Reference Jiménez and McMeeking42, Reference Jiménez and McMeeking55]. Based on the work by ref. [Reference Jiménez and McMeeking55] and assuming incompressibility, the resulting equation for deformation-dependent dielectric permittivity in the
$i$
-direction (i = 1,2,3),
$\varepsilon _i$
, was found to be:
\begin{equation} \frac{\varepsilon _i}{\varepsilon _0}= 1+\kappa [1+1/3(I_1/I_m)+1/3(I_1/I_m)^2]\!\left(\lambda _i^2-\frac{1}{3}I_1\right), \end{equation}
where
$\varepsilon _0$
is the undeformed permittivity,
$\kappa$
is the ratio electrostrictive coefficient to the undeformed permittivity of the incompressible material,
$\lambda _i$
is the stretch in the
$i$
-direction of the membrane (see Fig. 1), and
$I_1$
and
$I_m$
are the regular and the limiting stretch first stretch invariants, respectively. Models similar to that in Eq. (1) could, for example, be used to develop and represent materials with tunable dielectric or optical properties. Similarly, Cohen et al. [Reference Cohen, Oren and deBotton49] presented a model following a microstructurally motivated approach. In the limit of small electric fields and uniaxial deformation, they determined the relative permittivity,
$\varepsilon _r$
, to be:
\begin{equation} \varepsilon _r = \chi _0\!\left(1-\frac{1}{5n}\left(\lambda _{\text{uniaxial}}^2-\frac{1}{\lambda _{\text{uniaxial}}}\right)\right)+1 \end{equation}
where
$\chi _0 = \frac{\zeta N_0 K}{\Theta }$
is the initial susceptibility,
$\zeta$
is the persistence length of the polymer chains,
$N_0$
is the referential chain density,
$K$
is the number of monomers in a chain,
$\lambda _{\text{uniaxial}}$
is the uniaxial stretch, and
$\Theta$
is the absolute temperature in Kelvins.
Besides deformation dependence, other models have been developed to explore thermal dependency such as in ref. [Reference Sheng, Chen, Li and Wang56], which utilizes a framework based on the Debye model (DM) for the dielectric constant of a gas. While the DM relationship accounts for the temperature dependence of the dielectric permittivity, the model developed in ref. [Reference Sheng, Chen, Li and Wang56] was empirical. Their approach consisted of using experimental data produced by ref. [Reference Jean-Mistral, Sylvestre, Basrour and Chaillout45], a squared-law prestretch-permittivity relationship, and the DM to empirically fit the following expression:
\begin{equation} \varepsilon _3 = \alpha \lambda _{\text{biaxial}}^2+\frac{\beta }{\Theta } + \gamma \end{equation}
where
$\lambda _{\text{biaxial}}$
refers to a planar (biaxial) stretch, and
$\alpha$
,
$\beta$
, and
$\gamma$
are empirical constants. In the Section 4, temperature-independent conditions are assumed to be consistent with the scope of the current work, and Eq. (1) will be used to model the deformation response of the dielectric permittivity. Other permittivity-varying models are provided in the references in Table I.
2.2. Hyperelastic material models
The mechanical properties of the hyperelastic material can be described by a multitude of possible strain energy density functions. To predict the mechanical behavior of the material, the neo-Hookean (NH) [Reference Treloar71], Ogden (OM) [Reference Ogden72], Yeoh (YM) [Reference Yeoh73], Gent (GM) [Reference Gent74], Arruda-Boyce (AB) [Reference Arruda and Boyce75], and the Edward–Vilgis (EV) [Reference Edwards and Vilgis76] hyperelastic models are compared with experimental data. The interested reader is referred to read Appendix A to find descriptions and equations for each of the material models.
2.3. Employment of material models
For each material model, the mechanical (elastically storable) energy density,
$^{xy}W_S$
(see noteFootnote
5
), is added to the electrical energy density,
$W_{E}$
, to produce the total free energy density,
$W$
, or:
\begin{equation} W=\ ^{xy}W_{S}+W_{E}. \end{equation}
where
\begin{equation} W_{E}=\frac{1}{2}\varepsilon _3 E^2= \frac{1}{2}\frac{D^2}{\varepsilon _3}=\frac{1}{2}\frac{\tilde{D}^2}{\varepsilon _3}\lambda _1^{-2}\lambda _2^{-2}, \end{equation}
where
$E$
is the true electric field,
$D$
is the true electric displacement, and
$\tilde{D}$
is the nominal electric displacement. Also,
$\lambda _1$
and
$\lambda _2$
are the principal stretches in the 1- and 2-directions, respectively (see Fig. 1). Finally, note that
$\varepsilon _3$
refers to the dielectric permittivity in the through-thickness direction (refer to Fig. 1). Note that, although, the current work will ultimately include deformation-dependent permittivity [Eq. (1)], for the selection of the hyperelastic model (in the next section) constant values will be assumed. After that, the model will be expanded to include deformation-dependent permittivity by substituting Eq. (1) into Eq. (5) for the through-thickness permittivity (i = 3). Finally, the in-plane nominal stresses,
$s_1$
and
$s_2$
, and nominal electric field,
$\tilde{E}$
, are derived by taking partial derivatives of Eq. (4) w.r.t.
$\lambda _1$
,
$\lambda _2$
, and
$\tilde{D}$
, respectively, which results in:
\begin{equation} s_1 = \frac{\partial W}{\partial \lambda _1} \end{equation}
\begin{equation} s_2 = \frac{\partial W}{\partial \lambda _2} \end{equation}
\begin{equation} \tilde{E} = \frac{\partial W}{\partial \tilde{D}} \end{equation}
3. Deformation of a CDEA
To compare the various hyperelastic models (and for the remainder of this work), we analyze the OPD of a SCDEA.Footnote 6 Here, we provide a brief summary of the state equations. For more details, the interested reader can consult the reference work in [Reference He, Zhao and Suo28] and the easy-to-follow numerical framework proposed in [Reference Korn, Farmer and Medina58].
Consider the DEA configuration shown in Fig. 3. The elastomer begins at the undeformed state with outer radius,
$B$
, and inner radius,
$A$
, and thickness,
$T$
. The membrane is then prestretched,
$\lambda _p$
, a force,
$F$
, is applied to the center of the membrane, and an electric field,
$E$
, is applied through the thickness of the membrane resulting in OPD in the
$z$
direction, as shown in Fig. 3. The final position of a particle from the undeformed state,
$R$
, is determined by
$r(R)$
and
$z(R)$
.
The following system of four equations completely describes the motion of the system due to electrical and mechanical inputs. These equations, which are independent of material model, can be used to determine the state of any particle from the undeformed to the deformed membrane and are expressed as:
\begin{equation} \frac{dr}{dR}=\lambda _1\cos{\theta } \end{equation}
\begin{equation} \frac{dz}{dR}=-\lambda _1\sin{\theta } \end{equation}
\begin{equation} \frac{d\theta }{dR}=-\frac{s_2}{s_1R}\sin{\theta } \end{equation}
\begin{equation} 0=2\pi TRs_1\sin{\theta }-F \end{equation}
with the following boundary conditions (BCs):
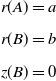\begin{equation} \begin{split} & r(A)=a\\[5pt] & r(B)=b\\[5pt] & z(B)=0 \end{split} \end{equation}
The first two BCs at
$r$
are defined by the radius of the inner,
$a$
, and outer,
$b$
, rigid supports, respectively. The condition at
$z$
is due to the definition of the
$r$
-
$z$
coordinate system. Furthermore, for convenience, the following dimensionless forms will be used when presenting the results:
$F_n = F/(2\pi aT\mu )$
and
$V_n = E/(\sqrt{\mu/\varepsilon })$
, where
$\mu$
is the shear modulus.
4. Results
4.1. Material model differences and selection
The hyperelastic material models considered (see Appendix A) were calibrated to a uniaxial tensile experiment for VHB4910 at a strain rate of 0.01 Hz (see Fig. 4a). Those models were used to compute the OPD behavior for the SCDEA shown in Fig. 4b. In general, the cone-like deformation observed results from a complex 3D stretch state (see Fig. 3). The
$\lambda _1$
and
$\lambda _3$
dominate the stretch state; however, the prestretch in the membrane affects also
$\lambda _2$
. Because of the complex stretch state, wrinkling of the membrane at locations close to the rigid disk (r = a) could occur at voltages near the breakdown voltage. With the maximum stretch state occurring near the rigid disk,
$\lambda _3$
is highly compressive in that region, resulting in an increased likelihood of dielectric breakdown due to membrane thinning. Toward the outer ring,
$\lambda _1$
decreases and approaches the prestretch value causing the membrane to transition from the highly compressive stretch state near the rigid disk to a less compressive state near the rigid support. With this state of affairs, the effects of the compressive Maxwell stress can cause higher stresses to be “felt” near the rigid disk (when compared to the outer edges) due to the membrane being thinner.
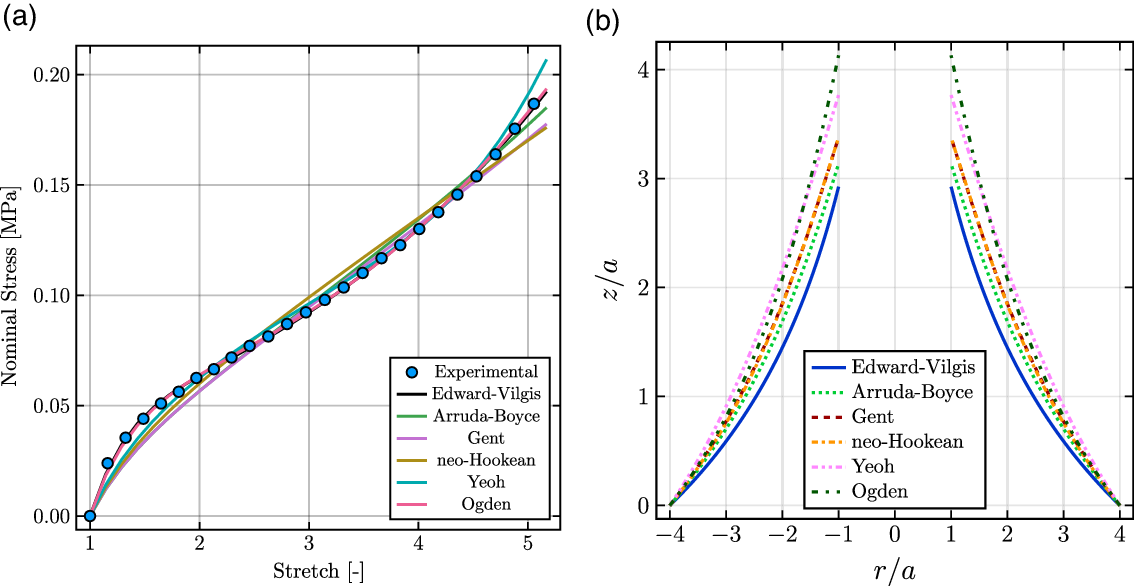
Figure 4. (a) Model predictions from a uniaxial tensile test of VHB4910 at 0.01 Hz. Note the Ogden and EV models almost overlap. (b) Comparison of various material models applied to the out-of-plane deformation of a SCDEA configuration. Only for this material selection step, the permittivity was assumed constant. Note the neo-Hookean model overlaps the Gent model predictions.
$V_n = 0.2$
,
$F_n = 2.0$
,
$\lambda _p = 2.0$
,
$b/a = 4.0$
.
For the example at hand (Fig. 3), the performance of the various hyperelastic models previously outlined (and briefly described in Appendix A) is compared. Best-fit curves are shown in Fig 4a and the model parameters are in Table II. The relative undeformed permittivity was taken to be 3.211 from ref. [36]. As shown in Fig. 4b, there are important differences in deformation among the various models, particularly near the inner disc. Only because of the high value of the limiting stretch invariant,
$J_m$
, the NH and GM models nearly overlap. An analysis of the effects of
$J_m$
on the maximum OPD was given in ref. [Reference Korn, Farmer and Medina58]. In general, and some minor exceptions, the OM seems to exhibit the highest deformation values while the EV model exhibits the lowest. When compared against either the AB or GM models, the EV model is said to model better strain-softening behaviors seen in DE materials (see Fig. 3 in ref. [Reference Mathew, Vo and Koh78]). Consideration of the effects due to sliplinks can be accounted as part of the cause for the difference exhibited by the EV model in comparison to the others, as shown in Fig. 4b. It is worth noting that the reported robustness of well-known models such as GM or AB was validated mainly for traditional rubber-like materials, without showing specific applications using softer DE materials, such as VHB4910/05. Furthermore, from observing the behavior of each of the material models, the results could indicate the need for the invariant-based phenomenological models to be fit to multiple stress-stretch tests, for more accurate implementation. For example, the large deformations observed for the model OM in Fig. 4b could be due to it being fit only to uniaxial stress data. Based on the aforementioned observations and the apparent advantages offered by the EV model to represent DE materials, in the sequel we use such a model for permittivity-varying analysis.
Table II. Material model parameters as obtained from a uniaxial stress-stretch test conducted at 0.01 Hz.
4.2. Effects of deformation-dependent permittivity
Figure 5 was developed using the EV model and stretch-dependent permittivity based on Eq. (1) and applied to the SCDEA example. Figure 5 shows the different effects of changing the electrostrictive coefficient ratio on the deformation state of the material. The electrostrictive coefficient was found to influence the maximum deformation along with the maximum stresses and stretches in the material. Of interest is the stress in the 1-direction and the electric field (see Figs. 5d and f). As the electrostrictive coefficient becomes more negative, the maximum stress and electric field in the membrane increase throughout and further increase near the inner rigid disk. With this increase in electric field and material stress, dielectric breakdown or tearing of the material becomes more likely to occur. When selecting a material for constructing a DEA, the consideration of the electrostrictive coefficient is found to be important for determining maximum voltages. It might be worth noticing the differences in
$\sigma _2$
between Fig. 5e, in the current work, and Fig. 4 in the work of He et al. [Reference He, Zhao and Suo28]. The general use of figures such as those shown in ref. [Reference He, Zhao and Suo28] as well as those Fig. 5 might be limited by the lack of other important parameters (e.g. the prestretch or material model parameters). Similarly, Fig. 6 shows how the prestretch state of the membrane influences the deformation and electrical state of the membrane. With increasing prestretches, the membrane follows the expected trend of larger stresses and stretches in the material. With the influence of the deformation-dependent permittivity, the stretches and stress are observed to increase with decreasing electrostrictive coefficient. For example, in Fig. 6a and c, the differences in the maximum stress and stretch state between the smallest and largest electrostrictive coefficients are significant that applying similar loadings to both cases would yield drastically different results with the material possibly failing in the case of a very negative electrostrictive coefficient. Furthermore, while the stretch in the
$2$
-direction does not show a large change among the electrostrictive coefficients, the stress,
$\sigma _2$
, changes rapidly with a decreasing electrostrictive coefficient (see Fig. 6b and d). The rapid increase in the maximum
$\lambda _2$
-stretch could contribute to an increased likelihood of material failure as a result of the sudden thinning. The importance of understanding the electrostrictive properties of a selected DE can help in the designing of soft actuators against material failure.
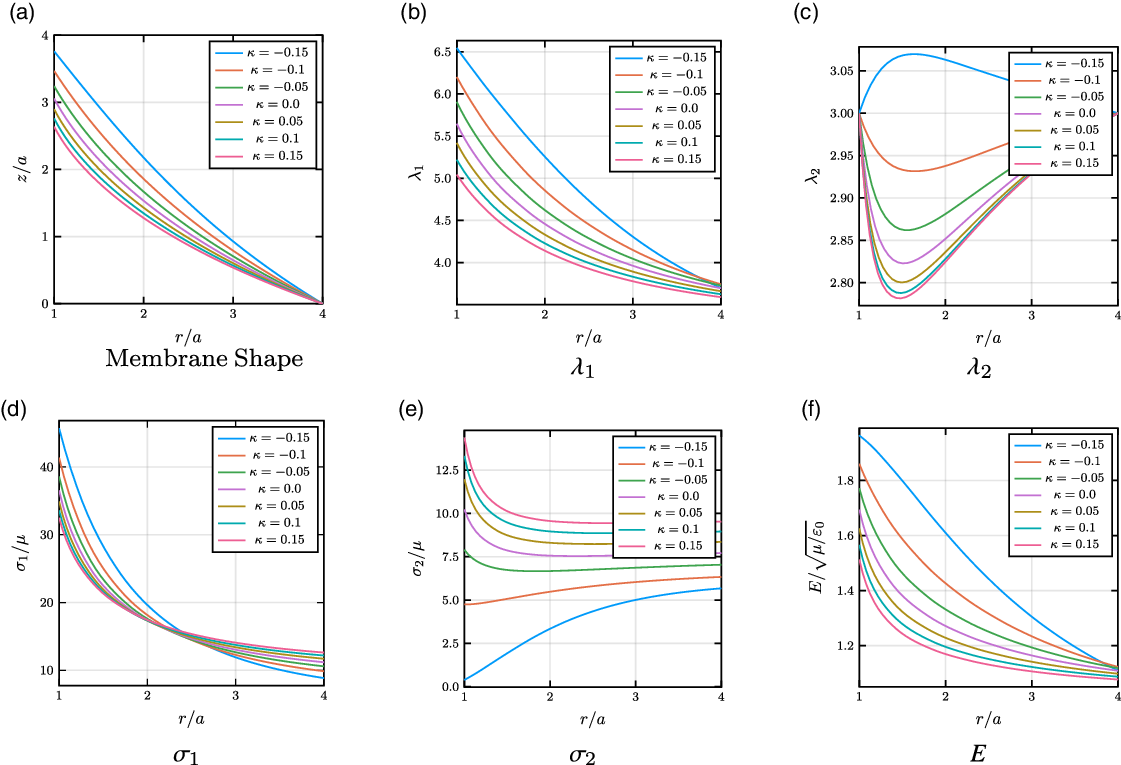
Figure 5. With decreasing electrostrictive coefficients, the maximum deformation increases (a) along with an increase in the stretches in the 1 and 2 directions (b–c). However, the stress in the 1-direction increases (d) while the stress in the 2-direction significantly decreases near the center of the cone (e). Furthermore, the electric field significantly increases near the center of the cone (f). The loading and geometry parameters are
$V_n = 0.1$
,
$F_n = 2.0$
,
$\lambda _p = 3.0$
,
$b/a = 4.0$
.
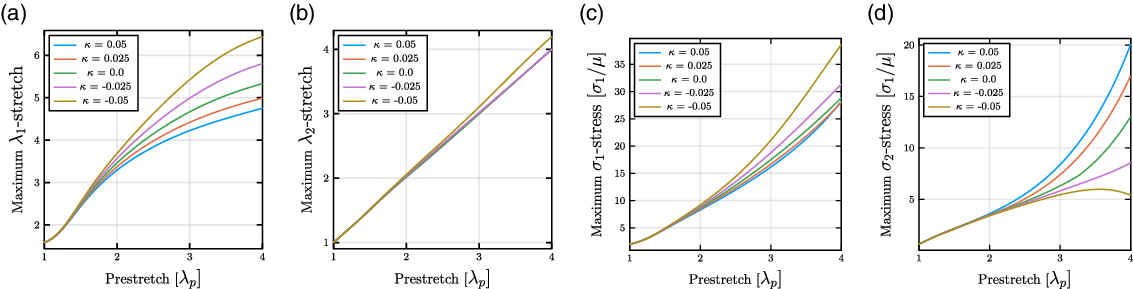
Figure 6. With an increase in the pre-stretch of the material, the maximum stretches and stress increase with a corresponding increase in applied voltage (a–c). However, due to nonlinearities with relation to the electrostrictive coefficient ratio, there is a critical value for certain negative electrostrictive coefficients where the maximum stress in the 2-direction now longer maximum stretches and stretches in the material as a result of varying the electrostrictive coefficient ratio and prestretched state. The simulations were performed with
$V_n = 0.15$
,
$F_n = 1.0$
,
$b/a = 4$
.
Next, the electrostrictive coefficient, applied voltage, and maximum deformation were analyzed to find parameters for achieving conditions of maximum OPD for a single-cone actuator (see Fig. 7). Figure 7b–d shows that for various
$\lambda _p$
, greater maximum deformations were shown to occur at lower voltages when the material had a more negative electrostrictive coefficient.
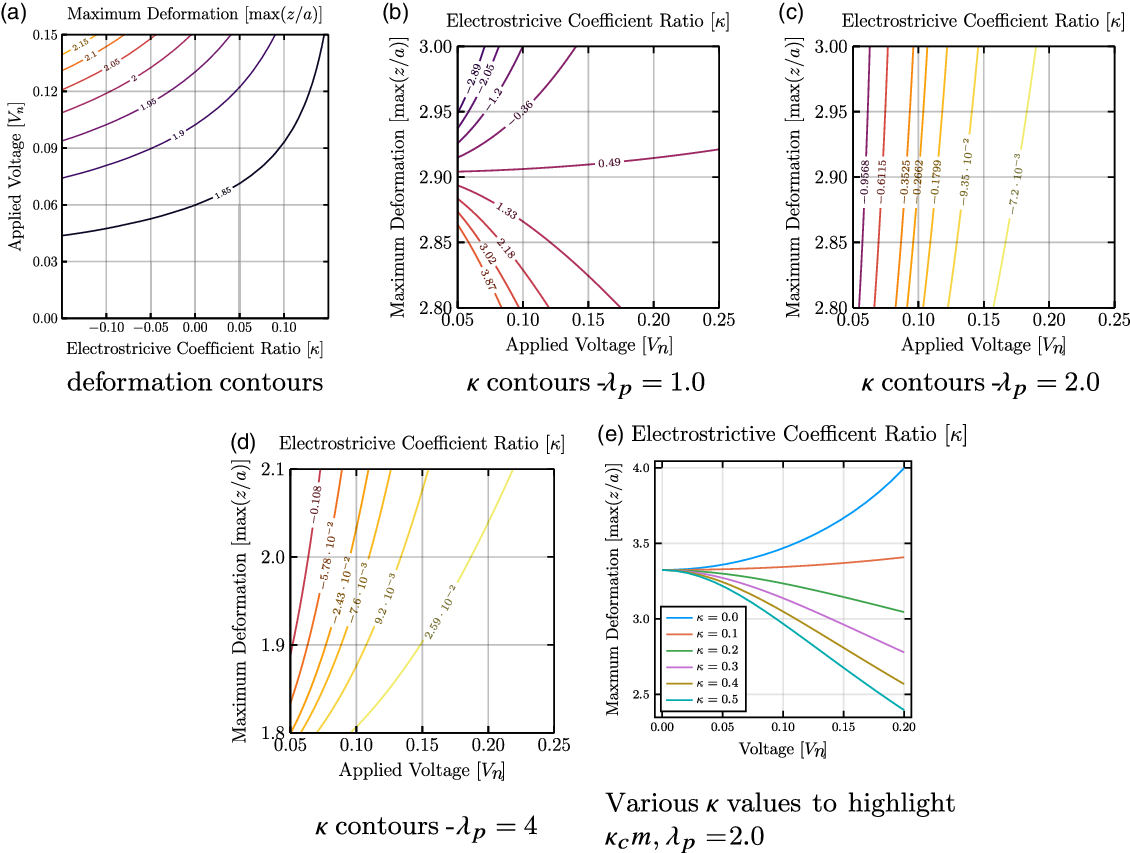
Figure 7. (a) The contour curves of maximum deformation dependent on the applied voltage and electrostrictive coefficient ratio. (b–d) Contours of electrostrictive coefficient to achieve a desired deformation at a specified voltage. (b) Near an electrostrictive coefficient value of 0.5, the maximum deformation of the membrane does not change. (c–d) As the prestretch increases, the linearity observed in (c) begins to disappear (d). (e) For any configuration of the material, an electrostrictive coefficient exists which results in minimal changes in the maximum deformation.
$F_n = 1.5$
,
$b/a = 4.0$
.
4.3. Analysis of critical kappa values
From Fig. 7b, at approximately
$\kappa = 0.5$
, the maximum OPD of the SCDEA does not change significantly with increasing voltage. Furthermore, the plot implies that there should a theoretical singular value of
$\kappa$
where the voltage applied does not affect the maximum deformation. This “stagnation” value should be considered in the design of DEA (as well as for DE sensors, for that matter). This theoretical stagnation
$\kappa$
will be named the critical mechanical electrostrictive coefficient ratio,
$\kappa _{\text{cm}}$
. The
$\kappa _{\text{cm}}$
value characterizes a specific combined material-and-loading configuration, for which the electromechanical coupling leads to minimum deformation. Figure 8 highlights a dependence of
$\kappa _{\text{cm}}$
on both the applied load and the prestretch. To further investigate parameters influencing the
$\kappa _{\text{cm}}$
value, a parametric study was conducted using symbolic regression from an open source package [Reference Cranmer79], which led to the following relationship:
\begin{equation} \kappa _{\text{cm}} = 1.03\sin \!\Big (\frac{0.778^{F_n^2}}{\lambda _p^2}\Big ) \end{equation}
Straightforward reduction and simplification of Eq. (9) can lead to a different expression:
\begin{equation} \kappa _{\text{cm}} =\frac{1}{\lambda _p^2}\!\left(1+\frac{1}{20\sqrt{\pi }}\right)\exp{\!\left (-\frac{F_n^2}{4}\right)} \end{equation}
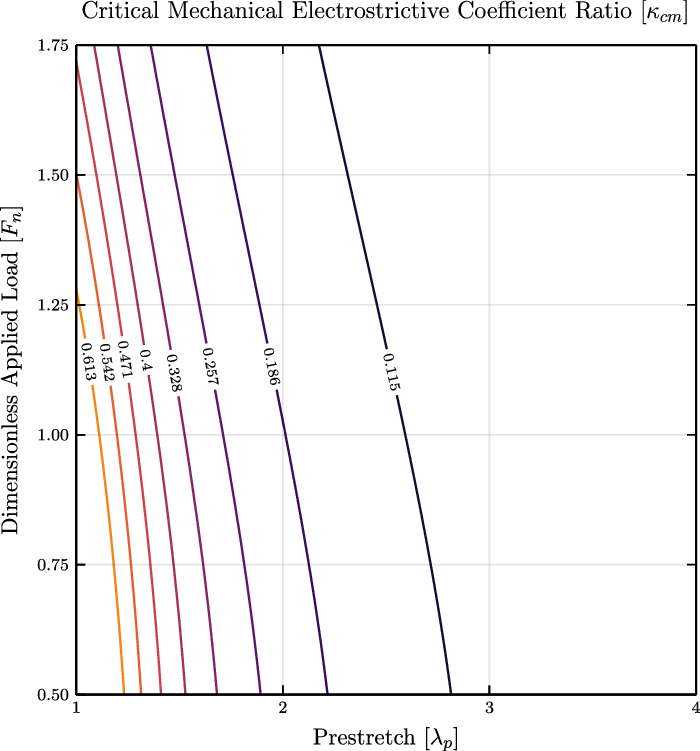
Figure 8. For larger prestretches, the critical mechanical electrostrictive coefficient ratio,
$\kappa\!$
cm, begins to decrease. As the applied force increases, the required critical mechanical coefficient decreases. For large prestretches and applied forces, an actuator could enter a state where deformation does not occur regardless of applied voltage limiting the usefulness of the system. Figure represents a system with
$b/a = 4$
.
These equations were verified to closely approximate the simulated data with a relative error below 10% for a moderate range of applied loads and a wide range of prestretches (see Fig. 9).
5. Discussion
5.1. Material model influence
The variety of available hyperelastic models creates a trade-off between accuracy, complexity, and interpretability. While simple models, like the NH, provide a view of the material, the accuracy is limited to small stretches. The phenomenological models, such as the Ogden and Yeoh, can be accurate when fit to multiple types of material tests; however, minimal microstructural information can be determined from the model’s parameters. In general, constitutive models could shed some light on the microstructure of the material even when parameters are found via macroscopic testing. For example, from Table II, within some limitations of interpretation,
$N_C^*$
and
$N_S^*$
values could indicate that there are more sliplinks than crosslinks per unit volume in the VHB4910 tested at 0.01 Hz strain rate. Further studies are recommended to explore the dependence of
$N_C^*$
and
$N_S^*$
on the strain rate.
The selection of EV model for this study was based on its potential to be fed from or provide microstructural insight of the material.
For the EVFootnote
7
model, the information provided by parameters about the microstructure could assist in understanding the response of the material to other environmental conditions such as humidity or temperature. It is important to note, however, that typically, models are fit to data from what is assumed to be a quasi-static tensile tests, as opposed to microstructure characterization via mechanical (such as AFM and SEM), chemical techniques, or ab initio computations. It is expected then, that for a typical viscoelastic material the model parameters do change depending on the strain rate (and temperature). Hence, EV parameters such as
$N_C^*$
and
$N_S^*$
are expected to be strain rate as well as temperature dependent.
5.2. Results from modeling with deformation-dependent permittivity
It is expected that the electrical and mechanical behaviors of the DE are intertwined. The traditional decoupling of these effects implies orthogonality on those behaviors. The addition of deformation-dependent permittivity has allowed a more careful study on how electromechanically induced effects can affect the limitations of the material. Furthermore, this approach gives rise to not only a critical electrical electrostrictive coefficient ratio but its mechanical counterpart. This modeling scheme produces two scenarios where the material is either limited mechanically or electrically. Mechanically, certain values of the electrostrictive coefficient ratio produce theoretical cases where deformation does not occur in response to a change in voltage. Electrically, certain cases are predicted where changes in capacitance cannot be measured in response to changes in deformation. The assumption of deformation-dependent permittivity produced new cases of material behavior which limit the effectiveness of DE membranes for applications in actuation and sensing. Furthermore, these revealed cases provide insight to both designers, about design constrains, and material scientists, about hypothetical materials that can be synthesized and with potential novel applications.
5.3. Impact of the critical mechanical electrostrictive coefficient ratio
The critical mechanical electrostrictive coefficient ratio provides opportunities for improving design frameworks involving DE materials for actuator configurations. The ratio reveals a region where the deformation is very small (even negligible) in response to voltage. The ratio highlights the intricate connection between the mechanical and electrical properties of the material. It is therefore limiting to the design process of DEAs to consider individually the electrical and mechanical properties. The deformation-dependent-permittivity paradigm allows for the consideration of both energy domains simultaneously.
The
$\kappa _{\text{cm}}$
is dependent not only on material properties and geometrical configuration but also on applied load. For a given set of properties and geometry, the loading conditions would influence the dynamic variation of this critical parameter. While the material may perform as expected under one set of operating condition, under a different but still feasible set of operating conditions the critical mechanical electrostrictive ratio may limit the final deformation of the membrane. It is recommended that for DE applications outside the laboratory environment, the full range of operating conditions should be explored to determine regions of inactivity.
5.4. Impact of a critical electrical electrostrictive coefficient ratio
The sensitivity of the capacitance was investigated to further understand the electromechanical implication of deformation-dependent permittivity, as applied to sensory systems. For the single-conical configuration, the capacitance,
$C$
, was determined using:
\begin{equation} C = \frac{2\pi }{T} \int _A^B \varepsilon \lambda _1^2 \lambda _2^2 R dR \end{equation}
The results for the capacitance are presented (see Fig. 10) in dimensionless form by dividing the undeformed capacitance,
$C_0$
:
\begin{equation} C_0 = \frac{2 \pi \varepsilon _0 (B^2 - A^2)}{T} \end{equation}
Analogous to the
$\kappa _{\text{cm}}$
value, which is related to the restraining of mechanical deformation, the capacitance has a set of nearly linear contour lines for a range of positive
$\kappa$
values. Hence, a critical electrical electrostrictive coefficient ratio,
$\kappa _{\text{ce}}$
, is introduced and it was shown to produce conditions of near-zero capacitance (see Fig. 10).
The aforementioned can be specially applicable when utilizing DEs as sensors. As the electrostrictive coefficient ratio becomes more negative, a greater variation in capacitance can be observed for changes in the applied load (see Fig. 10). These larger changes in capacitance relative to the undeformed capacitance could lead to improvements in sensitivity, and hence more accurate applications for either sensing or self-sensing DEs. Further research on the changes in capacitance sensitivity with respect to electrostrictive coefficient is recommended. Because the precision of DE-based sensors (including self-sensing configurations) relies on the ability to capture changes in measured capacitance to small changes in displacement of the DE, the electrostrictive characteristic of the selected polymeric material can be essential in the design of sensitive sensors.
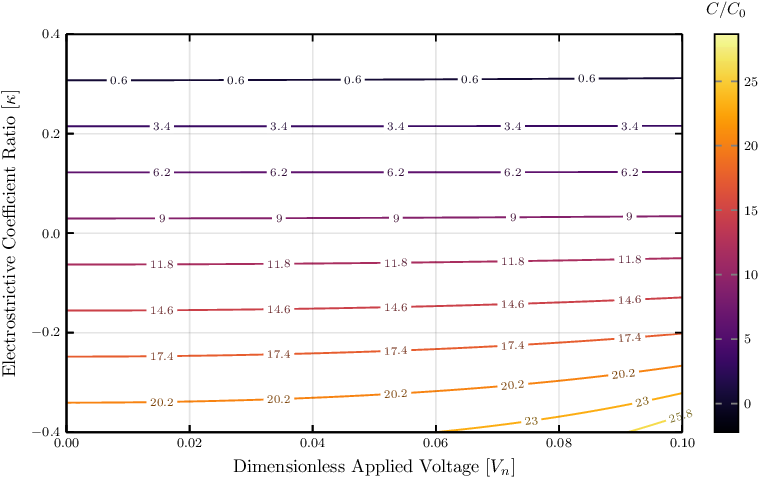
Figure 10. Contours of ratio of the deformed capacitance,
$C$
, and the undeformed capacitance,
$C_0$
, for a range of applied voltages and
$\kappa$
values.
$F_n = 1$
,
$b/a = 4$
,
$I_m = 230$
,
$\lambda _p = 2.0$
.
6. Conclusions
This work focuses on the contributions of a variable electrical permittivity for the OPD of a DEA membrane. First, an overview of the permittivity-varying models for DEs is provided. Then, from a list of some of the most common hyperelastic models used for DEs, the EV model was selected and utilized to analyze the OPD of the DEA through a range of electrostrictive coefficients. The DEA is shown to exhibit increased deformation for more negative electrostrictive coefficient values, which, even at low applied voltages, could lead to premature failure of the material. For negative electrostrictive coefficient values, the material exhibits a region of instability where the principal stress in the 2-direction transitions from tension to compression. Therefore, a singularity of zero stress must exist. From an analysis of contours showing the relationship between deformation and electrostrictive coefficient, a critical value was identified, which results in a “dead zone” of the electromechanical coupling in the DEA. This state of affairs reveals mechanisms that could be useful to actuator designers and developers. In addition, it creates an open gap for material scientists to explore.
Our results revealed that under some particular conditions and materials: (a) for actuators, an increase in applied voltage could lead to no change in the deformation state, which would not be desired for an actuator; (b) for sensors, changes in deformation would not lead to changes in capacitance. Those effects could be relevant where DEs are used as actuators (e.g. knee joints or robotic flapping wings) or as sensors where they provide tactile feedback. For either case, a loss of sensitivity to the applied stimulus could result in damage to the robot or environment.
Finally, since there are known analogous formulations between electrical and optical properties, a future research could include exploring the criticality principles studied in this article, but applied to optomechanical coupling, for example.
7. Nomenclature
-
$a$
rigid disk radius
-
$A$
position of a point on undeformed membrane that will end up at the outer edge of the rigid ring
-
$b$
rigid ring inner radius
-
$B$
position of a point on undeformed membrane that will end up at the inner edge of the rigid ring
-
$C_0$
undeformed capacitance
-
$C$
deformed capacitance
-
$C_i$
empirical constant for Yeoh model
-
$C_{ij}$
empirical constant for the Ogden models
-
$D$
true electric displacement
-
$\tilde{D}$
nominal electric displacement
-
$E$
true electric field
-
$\tilde{E}$
nominal electric field
-
$F$
force to deform conical dielectric elastomer actuator out of plane
-
$F_n$
dimensionless force
-
$h$
humidity
-
$I_1$
first strain invariant of the left Cauchy-Green deformation tensor
-
$I_m$
limiting first stretch invariant
-
$J_m$
limiting stretch invariant for the Gent model
-
$k$
Boltzmann constant
-
$K$
number of monomers per polymer chain
-
$l$
chain length
-
$M$
model order for the Ogden and Yeoh model
-
$n$
chain density
-
$N$
number of statistical links of length
$l$
-
$N_c$
number of crosslinks per volume
-
$N_c^*$
number of crosslinks per volume times the Boltzmann constant and absolute temperature
-
$N_s$
number of sliplinks per volume
-
$N_s^*$
number of sliplinks per volume times the Boltzmann constant and absolute temperature
-
$P$
AB material model constant
-
$r$
radial position on cone
-
$R$
point of interest on undeformed membrane
-
$T$
original thickness of the elastomer
-
$V$
electric potential (voltage)
-
$V_n$
dimensionless voltage
-
$W$
free energy density
-
$W_E$
dielectric energy density
-
$^{xy}W_S$
strain energy density for material model
$^{^{xy}}$
-
$Y$
small strain tensile modulus (Young’s Modulus)
-
$z$
vertical position on cone
-
$\alpha$
empirical coefficient
-
$\beta$
empirical coefficient
-
$\gamma$
empirical coefficient
-
$\lambda _i$
principal stress in
$i$
-direction-
$\dot{\lambda }$
strain rate
-
$\varepsilon _i$
deformation-dependent permittivity in the
$i$
-direction-
$\varepsilon _0$
undeformed permittivity
-
$\eta$
measure of slip strain
-
$\Theta$
absolute temperature
-
$\kappa$
electrostrictive coefficient ratio
-
$\kappa _{\text{cm}}$
critical mechanical electrostrictive coefficient ratio
-
$\kappa _{\text{ce}}$
critical electrical electrostrictive coefficient ratio
-
$\lambda _{\text{uniaxial}}$
uniaxial stretch
-
$\lambda _{\text{biaxial}}$
biaxial stretch
-
$\lambda _i$
principal stretch in the
$i$
-direction-
$\lambda _p$
prestretch
-
$\mu$
small strain shear modulus
-
$\sigma _i$
stress in the
$i$
-direction-
$\chi _0$
initial susceptibility
-
$\omega$
measure of chain inextensibility
-
$\zeta$
the persistence length of the polymer chains
Author contributions
Hector Medina and Carson Farmer conceived and designed the study. Carson Farmer conducted and analyzed the numerical experiments. Hector Medina and Carson Farmer wrote the article.
Financial support
The research was supported by internal grant from the Center for Research and Scholarship at Liberty University; Grant number 410024/B3610/UR1933.
Conflicts of interest
The authors declare none.
A. Appendix A: Discussion of Hyperelastic Models
Arruda-Boyce
The Arruda-Boyce (AB) model, also known as the 8-chain model, is based on a statistical mechanics treatment on the polymeric nature of the elastomeric material [Reference Arruda and Boyce75]. The model assumes that the elastomer is composed of sufficiently long molecular chains that are randomly oriented. Noting that for most practical applications, the number of chains is very large—thus allowing the use of the central limit theorem—one can assume the chain orientation to obey Langevin statistics [Reference Marckmann and Verron80]. Hence, the AB model can be expressed as:
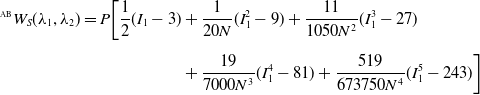\begin{equation} \begin{split} ^{\scriptscriptstyle \text{AB}}W_{S}(\lambda _1,\lambda _2)=P \bigg [\frac{1}{2}(I_1-3)&+\frac{1}{20 N}(I_1^2-9)+\frac{11}{1050 N^2}(I_1^3-27)\\[5pt] &+\frac{19}{7000 N^3}(I_1^4-81)+\frac{519}{673750 N^4}(I_1^5-243) \bigg ] \end{split} \end{equation}
Here
$P=nk\Theta$
, where
$n$
is the chain density and
$k$
is the Boltzmann constant;
$N$
is the number of statistical links of a particular length, say
$l$
(see note),Footnote
8
in the chain between chemical crosslinks.
Gent
The Gent model (GM) [Reference Gent74] can be considered a hybrid type of model.Footnote 9 Boyce [Reference Boyce81] compared it against their AB model and highlighted that while the two models perform comparably, the AB provides the extra ability to extend uniaxial-data fitting to other stress states [Reference Boyce81].
The GM was originally proposed as:
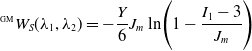\begin{equation} ^{\scriptscriptstyle \text{GM}}W_{S}(\lambda _1, \lambda _2) = -\frac{Y}{6} J_m \ln{\!\Bigg (1-\frac{I_1-3}{J_m}\Bigg )} \end{equation}
with two parameters:
$Y$
, the small strain tensile modulus, and
$J_m$
, the maximum value for
$I_1-3$
as the polymer chains reach their limiting stretched length.
neo-Hookean
The neo-Hookean (NH) material also falls under the physically/statistically motivated models [Reference Marckmann and Verron80] and can be derived from the GM. It describes well the behavior of hyperelastic materials only for small to moderate strains.
In terms of stretches, NH model can be expressed as:
\begin{equation} ^{\scriptscriptstyle \text{NH}}W_{S}(\lambda _1, \lambda _2, \lambda _3) = \frac{\mu }{2}(\lambda _1^2+\lambda _2^2+\lambda _3^2-3). \end{equation}
where
$\mu$
is the shear modulus. The NH model is readily implemented as it only requires a single parameter.
Ogden
The Ogden model (OM) is a phenomenological material model proposed in 1972 [Reference Marckmann and Verron80]. The model seeks to overcome some of the issues encountered with other invariant-based phenomenological models by increasing the effective range of stretches while decreasing their mathematical complexity [Reference Ogden72]. The OM takes the form:
\begin{equation} ^{\scriptscriptstyle \text{OM}}W_{S}(\lambda _1, \lambda _2,\lambda _3) = \sum _{i = i}^{M} \frac{C_{1i}}{C_{2i}}(\lambda _1^{C_{2i}}+\lambda _2^{C_{2i}}+\lambda _3^{C_{2i}}-3) \end{equation}
where
$C_{1i}$
and
$C_{2i}$
are best-fit constants with the stability condition
$C_{1i} C_{2i}\gt 0$
. Ogden determined that
$M=3$
provided a good fit that could be obtained through a set of simple tension, pure shear, and equibiaxial tension tests. Ogden found the model to be accurate up to a stretch of about 7 [Reference Ogden72]. The addition of further terms to Eq. (A4) increases the accuracy at the expense of potentially overfitting and even rendering the model unstable.
Yeoh
The Yeoh model (YM) [Reference Yeoh82], proposed in 1993, is another commonly utilized phenomenological model. It can be expressed as:
\begin{equation} ^{\scriptscriptstyle \text{YM}}W_{S}(\lambda _1, \lambda _2,\lambda _3) = \sum _{i = 1}^{M}C_i (\lambda _1^2+\lambda _2^2+\lambda _3^2-3)^i \end{equation}
where
$M=3$
and
$C_i$
are best-fit constants.
Edward-Vilgis
The Edward-Vilgis (EV) model was proposed in 1986 [Reference Edwards and Vilgis76]. In contrast to the previously discussed models, the EV model attempts to account for effects related to crosslinking, polymer chain length extension, polymer chain slippage, and polymer chain entanglement. The energy density associated with the hyperelastic model,
$^{\scriptscriptstyle \text{EV}}W_{S}$
was proposed as:
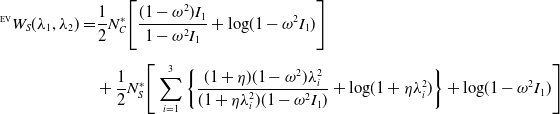\begin{equation} \begin{split} ^{\scriptscriptstyle \text{EV}}W_{S}(\lambda _1, \lambda _2) = & \frac{1}{2}N_C^*\Bigg [\frac{(1-\omega ^2)I_1}{1-\omega ^2I_1}+\log\!(1-\omega ^2I_1)\Bigg ]\\[5pt] & +\frac{1}{2}N_S^*\Bigg [\sum _{i=1}^{3}\left\{\frac{(1+\eta )(1-\omega ^2)\lambda _i^2}{( 1+\eta \lambda _i^2)(1-\omega ^2I_1)}+\log\!(1+\eta \lambda _i^2)\right \}+\log\!(1-\omega ^2I_1)\Bigg ] \end{split} \end{equation}
where:
$N_c^* = N_c k \Theta$
,
$N_s^* = N_s k \Theta$
, and
$N_c$
and
$N_s$
are the number of crosslinks and sliplinks per volume, respectively. Also,
$\omega$
provides a measure of the chain extensibility, and
$\eta$
provides a measure of the slip strain. The EV model has been found to predict both the initial strain-softening and later strain-stiffening effects in VHB 4905 [Reference Mathew, Vo and Koh78].
Open access
