Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T08:52:58.953Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of Hybrid Prandtl–Ishlinskii and Constitutive Models for Hysteresis of Shape-Memory-Alloy-Driven Actuators

Published online by Cambridge University Press:  04 February 2021

Saeid Shakiba Open the ORCID record for Saeid Shakiba [Opens in a new window] ,
Moosa Ayati Open the ORCID record for Moosa Ayati [Opens in a new window]  and
Aghil Yousefi-Koma Open the ORCID record for Aghil Yousefi-Koma [Opens in a new window]
Saeid Shakiba
Affiliation:
PhD Candidate, Center of Advanced Systems and Technologies (CAST), School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran
Moosa Ayati*
Affiliation:
Associate Professor, School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran
Aghil Yousefi-Koma
Affiliation:
Professor, Center of Advanced Systems and Technologies (CAST), School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Summary

Prandtl–Ishlinskii (PI) model has an excellent compromise to characterize an asymmetric saturated hysteresis behavior of shape-memory-alloy (SMA)-driven systems, but it cannot consider thermomechanical relations between components of SMA-driven systems. On the other hand, constitutive models are composed of these relations, but their precision needs to be improved. In this paper, PI model is proposed to boost constitutive models in two cases. In the first case, PI model is used to characterize martensite volume fraction (MVF) called hybrid model. In the second case, the model is applied as a regulator in the output of a constitutive model called PI-based output (PIO) regulator. Due to simplicity and ability of Liang–Rogers (LR) model in transformation phases, it is considered as an MVF in the original constitutive model. The performance of both proposed models is compared with the original LR-based constitutive model. Unknown parameters of all three models are identified using genetic algorithm in MATLAB Toolbox. The performance of the three models is investigated at three different frequencies of 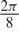\[\frac{{2\pi }}{8}\], 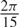\[\frac{{2\pi }}{{15}}\], and 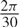\[\frac{{2\pi }}{{30}}\] Hz because the excitation frequency changes the hysteresis behavior. Results show that the proposed hybrid model keeps the precision of the original constitutive model at different frequencies. In addition, the proposed PIO model shows the best performance to predict hysteresis behavior at different frequencies.

Keywords

Prandtl–IshlinskiiHybrid modelHysteresisConstitutive modelLiang–RogersShape memory alloy
Type
Article
Information
Robotica , Volume 39 , Issue 8 , August 2021 , pp. 1390 - 1404
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Knick, C. R., Sharar, D. J., Wilson, A. A., Smith, G. L., Morris, C. J. and Bruck, H. A., “High frequency, low power, electrically actuated shape memory alloy MEMS bimorph thermal actuators,” J. Micromech. Microeng. 29(7), 075005 (2019).CrossRefGoogle Scholar
Botshekanan Dehkordi, M., “Modeling of simultaneous shape memory and pseudoelastic effects of shape memory alloys on nonlinear dynamic response of multilayer composite plate embedded with pre-strained SMA wires under thermal condition,” Mech. Adv. Mater. Struct. 26(16), 1411–1422 (2019).CrossRefGoogle Scholar
Lu, Y., Xie, Z., Wang, J., Yue, H., Wu, M. and Liu, Y., “A novel design of a parallel gripper actuated by a large-stroke shape memory alloy actuator,” Int. J. Mech. Sci. 159, 74–80 (2019).CrossRefGoogle Scholar
Hadi, A., Yousefi-Koma, A., Moghaddam, M. M., Elahinia, M. and Ghazavi, A., “Developing a novel SMA-actuated robotic module,” Sens. Actuators, A 162(1), 72–81 (2010).CrossRefGoogle Scholar
Williams, E. and Elahinia, M. H., “An automotive SMA mirror actuator: modeling, design, and experimental evaluation,” (in English), J. Intell. Mater. Syst. Struct. 19(12), 1425–1434 (2008).CrossRefGoogle Scholar
AbuZaiter, A., Nafea, M., Faudzi, A. A. M., Kazi, S. and Ali, M. S. M., “Thermomechanical behavior of bulk NiTi shape-memory-alloy microactuators based on bimorph actuation,” Microsyst. Technol. 22(8), 2125–2131 (2016).CrossRefGoogle Scholar
Sayyaadi, H., Zakerzadeh, M. R. and Zanjani, M. A. V., “Accuracy evaluation of generalized Prandtl-Ishlinskii model in characterizing asymmetric saturated hysteresis nonlinearity behavior of shape memory alloy actuators,” Int. J. Res. Rev. Mechatronic Des. Simul. (IJRRMDS). 1, 59–68 (2011).Google Scholar
Shakiba, S., Zakerzadeh, M. R. and Ayati, M., “Experimental characterization and control of a magnetic shape memory alloy actuator using the modified generalized rate-dependent Prandtl–Ishlinskii hysteresis model,” Proc. Inst. Mech. Eng. Part I: J. Syst. Control Eng. 232(5), 506–518 (2018).Google Scholar
Shakiba, S., Yousefi-Koma, A., Jokar, M., Zakerzadeh, M. R. and Basaeri, H., “Modeling and characterization of the shape memory alloy–based morphing wing behavior using proposed rate-dependent Prandtl-Ishlinskii models,” Proc. Inst. Mech. Eng. Part I: J. Syst. Control Eng. 234(4), 550–565 (2020).Google Scholar
Shakiba, S., Yousefi-Koma, A. and Ayati, M., “Tracking control of an SMA-driven actuator with rate-dependent behavior using an inverse model of hysteresis,” J. Braz. Soc. Mech. Sci. Eng. 42(8), 1–15 (2020).CrossRefGoogle Scholar
Brinson, L. C., “One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable,” J. Intell. Mater. Syst. Struct. 4(2), 229–242 (1993).CrossRefGoogle Scholar
Rogers, C. A., Liang, C. and Fuller, C. R., “Modeling of shape memory alloy hybrid composites for structural acoustic control,” J. Acoust. Soc. Am. 89(1), 210–220 (1991).CrossRefGoogle Scholar
Tanaka, K., Kobayashi, S. and Sato, Y., “Thermomechanics of transformation pseudoelasticity and shape memory effect in alloys,” Int. J. Plast. 2(1), 59–72 (1986).CrossRefGoogle Scholar
Lu, Y., Zhang, R., Xu, Y., Wang, L. and Yue, H., “Resistance characteristics of SMA actuator based on the variable speed phase transformation constitutive model,” Materials. 13(6), 1479 (2020).CrossRefGoogle ScholarPubMed
Lu, Y., Zhang, R., Xie, Z., Yue, H. and Wang, L., “A new variable speed phase transformation constitutive model of shape memory alloys,” Mater. Res. Express 6(10), 105705 (2019).CrossRefGoogle Scholar
Mirzakhani, F., Ayati, S., Fahimi, P. and Baghani, M., “Online force control of a shape-memory-alloy-based 2 degree-of-freedom human finger via inverse model and proportional–integral–derivative compensator,” J. Intell. Mater. Syst. Struct. 30(10), 1538–1548 (2019).CrossRefGoogle Scholar
Elahinia, M. H. and Ahmadian, M., “An enhanced SMA phenomenological model: I. The shortcomings of the existing models,” Smart Mater. Struct. 14(6), 1297 (2005).CrossRefGoogle Scholar
Mehrabi, R., Shirani, M., Kadkhodaei, M. and Elahinia, M., “Constitutive modeling of cyclic behavior in shape memory alloys,” Int. J. Mech. Sci. 103, 181–188 (2015).CrossRefGoogle Scholar
Shirani, M., Andani, M. T., Kadkhodaei, M. and Elahinia, M., “Effect of loading history on phase transition and martensitic detwinning in shape memory alloys: limitations of current approaches and development of a 1D constitutive model,” J. Alloys Compd. 729(2017), 390–406 (2017).CrossRefGoogle Scholar
Shakiba, S., Yousefi-Koma, A. and Ayati, M., “Development of a frequency-dependent constitutive model for hysteresis of shape memory alloys,” In: Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications 234(12), 1535–1549 (2020).Google Scholar
Sayyaadi, H. and Zakerzadeh, M. R., “Position control of shape memory alloy actuator based on the generalized Prandtl–Ishlinskii inverse model,” Mechatronics 22(7), 945–957 (2012).CrossRefGoogle Scholar
Zakerzadeh, M. R. and Sayyaadi, H., “Precise position control of shape memory alloy actuator using inverse hysteresis model and model reference adaptive control system,” Mechatronics. 23(8), 1150–1162 (2013).CrossRefGoogle Scholar
Liang, C. and Rogers, C., “One-dimensional thermomechanical constitutive relations for shape memory materials,” J. Intell. Mater. Syst. Struct. 8(4), 285–302 (1997).CrossRefGoogle Scholar
Elahinia, M. H. and Ahmadian, M., “An enhanced SMA phenomenological model: II. The experimental study,” Smart Mater. Struct. 14(6), 1309 (2005).CrossRefGoogle Scholar
Basaeri, H., Yousefi-Koma, A., Zakerzadeh, M. R. and Mohtasebi, S. S., “Experimental study of a bio-inspired robotic morphing wing mechanism actuated by shape memory alloy wires,” Mechatronics 24(8), 1231–1241 (2014).CrossRefGoogle Scholar