Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-31T20:27:39.418Z Has data issue: false hasContentIssue false
  • English
  • Français

UNFOLDING FINITIST ARITHMETIC

Published online by Cambridge University Press:  11 August 2010

SOLOMON FEFERMAN  and
THOMAS STRAHM
SOLOMON FEFERMAN*
Affiliation:
Stanford University
THOMAS STRAHM*
Affiliation:
University of Bern
*
*DEPARTMENT OF MATHEMATICS, STANFORD UNIVERSITY, STANFORD, CA 94305. E-mail: [email protected]
†INSTITUT FÜR INFORMATIK UND ANGEWANDTE MATHEMATIK, UNIVERSITÄT BERN, NEUBRÜCKSTRASSE 10, CH-3012 BERN, SWIZTERLAND. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The concept of the (full) unfolding 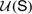of a schematic system 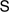is used to answer the following question: Which operations and predicates, and which principles concerning them, ought to be accepted if one has accepted 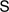? The program to determine 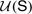for various systems 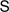of foundational significance was previously carried out for a system of nonfinitist arithmetic, 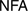; it was shown that 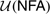is proof-theoretically equivalent to predicative analysis. In the present paper we work out the unfolding notions for a basic schematic system of finitist arithmetic, 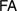, and for an extension of that by a form 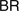of the so-called Bar Rule. It is shown that 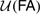and 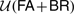are proof-theoretically equivalent, respectively, to Primitive Recursive Arithmetic, 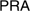, and to Peano Arithmetic, .

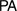Type
Research Article
Information
The Review of Symbolic Logic , Volume 3 , Issue 4 , December 2010 , pp. 665 - 689
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Beeson, M. J. (1985). Foundations of Constructive Mathematics: Metamathematical Studies. Berlin, Germany: Springer.CrossRefGoogle Scholar
Feferman, S. (1975). A language and axioms for explicit mathematics. In Crossley, J., editor. Algebra and Logic, Volume 450 of Lecture Notes in Mathematics. Berlin, Germany: Springer, pp. 87–139.Google Scholar
Feferman, S. (1996). Gödel’s program for new axioms: Why, where, how and what? In Hájek, P., editor. Gödel ’96, Volume 6 of Lecture Notes in Logic. Berlin, Germany: Springer, pp. 3–22.Google Scholar
Feferman, S., Baaz, M., Papadimitriou, C. H., Putnam, H., Scott, D., & Harper, C. L. Jr. Lieber Herr Bernays!, Lieber Herr Gödel!. Gödel on finitism, constructivity and Hilbert’s program. In Baaz, M., et al. , editor. Horizons of Truth: Logics, Foundations of Mathematics, and the Quest for Understanding the Nature of Knowledge. New York: Cambridge University Press. Reprinted in Dialectica 62 (2008), 179–203.Google Scholar
Feferman, S., & Strahm, T. (2000). The unfolding of non-finitist arithmetic. Annals of Pure and Applied Logic, 104(1–3), 75–96.CrossRefGoogle Scholar
Feferman, S., & Strahm, T. (2001). Unfolding finitist arithmetic (Abstract). Bulletin of Symbolic Logic, 7(1), 111–112.Google Scholar
Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme. Monatshefte für Mathematik und Physik, 38, 173–198.CrossRefGoogle Scholar
Gödel, K. (1995). In Feferman, S., Dawson, J. W. Jr., Goldfarb, W., Parsons, C., & Solovay, R. N. Collected Works Vol. III. New York: Oxford University Press.Google Scholar
Gödel, K. (2003). In Feferman, S., Dawson, J. W. Jr., Goldfarb, W., Parsons, C., & Sieg, W.Collected Works Vol. IV. Oxford: Clarendon Press.Google Scholar
Hilbert, D., & Bernays, P. (1968). Grundlagen der Mathematik (2nd edition), Vol. I. Berlin, Germany: Springer.Google Scholar
Hilbert, D., & Bernays, P. (1970). Grundlagen der Mathematik (2nd edition), Vol. II. Berlin, Germany: Springer.CrossRefGoogle Scholar
Kreisel, G. (1960). Ordinal logics and the characterization of informal concepts of proof. In Todd, J. A., editor. Proceedings International Congress of Mathematicians, 14–21 August 1958. Cambridge: Cambridge University Press, pp. 289–299.Google Scholar
Kreisel, G. (1965). Mathematical logic. In Saaty, T. L., editor. Lectures on Modern Mathematics, Vol. 3. New York: Wiley, pp. 95–195.Google Scholar
Kreisel, G. (1970). Principles of proof and ordinals implicit in given concepts. In Kino, A., Myhill, J., and Vesley, R. E., editors. Intuitionism and Proof Theory. Amsterdam, The Netherlands: North Holland, pp. 489–516.Google Scholar
Mints, G. (1973). Quantifier-free and one-quantifier systems. Journal of Soviet Mathematics, 1, 71–84.Google Scholar
Parsons, C. (1970). On a number theoretic choice schema and its relation to induction. In Myhill, J., Kino, A., and Vesley, R., editors. Intuitionism and Proof Theory, Proceedings of the Summer Conference at Buffalo N.Y., 1968. Amsterdam, The Netherlands: North Holland, pp. 459–473.CrossRefGoogle Scholar
Parsons, C. (1998). Finitism and intuitive knowledge. In Schirn, M., editor. The Philosophy of Mathematics Today. Oxford: Oxford University Press, pp. 249–270.Google Scholar
Sieg, W. (1985). Fragments of arithmetic. Annals of Pure and Applied Logic, 28, 33–71.CrossRefGoogle Scholar
Strahm, T. (2000). The non-constructive μ operator, fixed point theories with ordinals, and the bar rule. Annals of Pure and Applied Logic, 104(1–3), 305–324.CrossRefGoogle Scholar
Tait, W. (1961). Nested recursion. Mathematische Annalen, 143, 236–250.CrossRefGoogle Scholar
Tait, W. (1968). Constructive reasoning. In van Rootselaar, B., and Staal, J. F., editors. Logic, Methodology and Philosophy of Science III. Amsterdam, The Netherlands: North Holland, pp. 185–199.CrossRefGoogle Scholar
Tait, W. (1981). Finitism. Journal of Philosophy, 78, 524–546.CrossRefGoogle Scholar
Tait, W. (2005). The Provenance of Pure Reason. New York: Oxford University Press.Google Scholar
Tait, W. (2006a). Gödel’s correspondence on proof theory and constructive mathematics. Philosophia Mathematica (III), 14, 76–111.CrossRefGoogle Scholar
Tait, W. (2006b). Wellfoundedness of exponentiation. Personal communication.Google Scholar
Troelstra, A., & van Dalen, D. (1988). Constructivism in Mathematics, Vol. I. Amsterdam, The Netherlands: North-Holland.Google Scholar
Zach, R. (2003). Hilbert’s Program. Stanford Encyclopedia of Philosophy. Available from: http://plato.stanford.edu/entries/hilbert-program/.Google Scholar
Zach, R. (2006). Hilbert’s program then and now. In Jacquette, D., editor. Philosophy of Logic, Volume 5 of Handbook of the Philosophy of Science. Amsterdam, The Netherlands: Elsevier, pp. 411–447.Google Scholar