Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T08:07:31.804Z Has data issue: false hasContentIssue false
  • English
  • Français

DECIDABILITY OF INDEPENDENCE-FRIENDLY MODAL LOGIC

Published online by Cambridge University Press:  13 July 2010

MERLIJN SEVENSTER
MERLIJN SEVENSTER*
Affiliation:
Philips Research
*
*PHILIPS RESEARCH, PROF. HOLSTLAAN 4, 5656AA EINDHOVEN, THE NETHERLANDS E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider an independence-friendly modal logic, IFML. It follows from results in the literature that qua expressive power, IFML is a fragment of second-order existential logic, 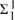, that cannot be translated into first-order logic. It is also known that IFML lacks the tree structure property. We show that IFML has the ‘truncated structure property’, a weaker version of the tree structure property, and that its satisfiability problem is solvable in 2NEXP. This implies that this paper reveals a new decidable fragment of . We also show that IFML becomes undecidable if we add the identity symbol to its vocabulary by means of a reduction from the tiling problem.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 3 , Issue 3 , September 2010 , pp. 415 - 441
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Andréka, H., van Benthem, J. F. A. K., & Németi, I. (1998). Modal languages and bounded fragments of predicate logic. Journal of Philosophical Logic, 27, 217–274.CrossRefGoogle Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge, UK: Cambridge University Press.CrossRefGoogle Scholar
Blackburn, P., & Seligman, J. (1995). Hybrid languages. Journal of Logic, Language and Information, 4(3), 251–272.CrossRefGoogle Scholar
Blackburn, P., & van Benthem, J. F. A. K. (2007). Modal logic: A semantic perspective. In Blackburn, P., van Benthem, J. F. A. K., and Wolter, F., editors. Handbook of Modal Logic, Volume 3 of Studies in Logic and Practical Reasoning. Amsterdam, The Netherlands: Elsevier, pp. 1–84.Google Scholar
Harel, D. (1985). Recurring dominoes: Making the highly undecidable highly understandable. Annals of Discrete Mathematics, 24, 51–72.Google Scholar
Hintikka, J. (1996). Principles of Mathematics Revisited. Cambridge, UK: Cambridge University Press.CrossRefGoogle Scholar
Hintikka, J., & Sandu, G. (1997). Game-theoretical semantics. In van Benthem, J. F. A. K., and ter Meulen, A., editors. Handbook of Logic and Language. Amsterdam, The Netherlands: North Holland, pp. 361–481.CrossRefGoogle Scholar
Hodges, W. (1997). Compositional semantics for a language of imperfect information. Logic Journal of the IGPL, 5(4), 539–563.CrossRefGoogle Scholar
Horrocks, I., Hustadt, U., Sattler, U., & Schmidt, R. (2007). Computational modal logic. In Blackburn, P., van Benthem, J. F. A. K., and Wolter, F., editors. Handbook of Modal Logic. Amsterdam, The Netherlands: Elsevier, pp. 181–245.CrossRefGoogle Scholar
Hyttinen, T., & Tulenheimo, T. (2005). Decidability of IF modal logic of perfect recall. In Schmidt, R., Pratt-Hartmann, I., Reynolds, M., and Wansing, H., editors. Advances in Modal Logic, Vol. 5. London, UK: King’s College Publications, pp. 111–131.Google Scholar
Janssen, T. M. V. (2002). Independent choices and the interpretation of IF logic. Journal of Logic, Language and Information, 11, 367–387.CrossRefGoogle Scholar
Papadimitriou, C. H. (1994). Computational Complexity. Reading, MA: Addison-Wesley.Google Scholar
Peterson, G., Azhar, S., & Reif, J. H. (2001). Lower bounds for multiplayer noncooperative games of incomplete information. Computers and Mathematics with Applications, 41, 957–992.CrossRefGoogle Scholar
Sandu, G. (1993). On the logic of informational independence and its applications. Journal of Philosophical Logic, 22(1), 29–60.CrossRefGoogle Scholar
Sevenster, M. (2009). Model-theoretic and computational properties of modal dependence logic. Journal of Logic and Computation, 19(6), 1157–1173.CrossRefGoogle Scholar
Sevenster, M. (2006). Branches of Imperfect Information: Logic, Games, and Computation. Ph. D. thesis, ILLC, Universiteit van Amsterdam.Google Scholar
Tulenheimo, T. (2004). Independence-friendly modal logic. PhD Thesis, University of Helsinki, Finland.Google Scholar
Tulenheimo, T., & Sevenster, M. (2006). On modal logic, IF logic and IF modal logic. In Hodkinson, I., and Venema, Y., editors. Advances in Modal Logic, Vol. 6. London, UK: College Publications, pp. 481–501.Google Scholar
Väänänen, J. (2008). Modal dependence logic. In Apt, K., and van Rooij, R. A. M., editors. New Perspectives on Games and Interaction, Vol. 5. Amsterdam, The Netherlands: Amsterdam University Press, pp. 237–254.Google Scholar
van Benthem, J. F. A. K. (1976). Modal correspondence theory. PhD Thesis, Mathematisch Instituut & Instituut voor Grondlagenonderzoek, Universiteit van Amsterdam.Google Scholar
van Emde Boas, P. (1996). The Convenience of Tiling. Ct-96-01, ILLC, Amsterdam, The Netherlands: University of Amsterdam.Google Scholar
Vardi, M. Y. (1996). Why is modal logic so robustly decidable? In Immerman, N., and Kolaitis, P. G., editors. Descriptive Complexity and Finite Models, Volume 31 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science. Washington, DC, USA: American Mathematical Society, pp. 149–184.Google Scholar
Walkoe, W. (1970). Finite partially-ordered quantification. Journal of Symbolic Logic, 35(4), 535–555.CrossRefGoogle Scholar