No CrossRef data available.
Published online by Cambridge University Press: 26 February 2010
We prove that every first-order formula that is invariant under quasi-injective bisimulations is equivalent to a formula of the hybrid logic 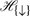 . Our proof uses a variation of the usual unravelling technique. We also briefly survey related results, and show in a standard way that it is undecidable whether a first-order formula is invariant under quasi-injective bisimulations.
. Our proof uses a variation of the usual unravelling technique. We also briefly survey related results, and show in a standard way that it is undecidable whether a first-order formula is invariant under quasi-injective bisimulations.