Ordered binary decision diagrams (OBDDs) and several more general BDD models have turned out to be representations of Boolean functions which are useful in applications like verification, timing analysis, test pattern generation or combinatorial optimization.The hidden weighted bit function (HWB) is of particular interest, since it seems to be the simplest function with exponential OBDD size. The complexity of this function with respect to different circuit models, formulas, and various BDD models is discussed.

A simplified proof is given for the following result due to Lisovik: it is undecidable for two given ε–free finitesubstitutions, whether they are equivalent on the regular languageb{0,1}* c.

We study D0L power series over commutative semirings. We show that a sequence(cn )n≥0 of nonzero elements of a field A is the coefficientsequence of a D0L power series if and only if there exist a positive integerk and integers βi for 1 ≤ i ≤ k such that $c_{n+k}=c_{n+k-1}^{\beta_1}c_{n+k-2}^{\beta_2}\ldots c_n^{\beta_k}$ for alln ≥ 0. As a consequence we solve the equivalence problem of D0L powerseries over computable fields.

A deterministic automaton recognizing a givenω-regular languageis constructed from an ω-regular expressionwith the help of derivatives.The construction is related to Safra's algorithm, in about the same way as the classicalderivative method is related to the subset construction.

Ko [26] and Bruschi [11] independently showed that, insome relativized world, PSPACE (in fact, ⊕P) contains a setthat is immune to the polynomial hierarchy (PH). In this paper, westudy and settle the question of relativized separations withimmunity for PH and the counting classes PP, ${\rm C\!\!\!\!=\!\!\!P}$ , and ⊕Pin all possible pairwise combinations. Our main result is that thereis an oracle A relative to which ${\rm C\!\!\!\!=\!\!\!P}$ contains a set that is immune BPP⊕P.In particular, this ${\rm C\!\!\!\!=\!\!\!P}^A$ set is immune to PHA and to ⊕PA. Strengthening results ofTorán [48] and Green [18], we also show that, in suitable relativizations, NP contains a ${\rm C\!\!\!\!=\!\!\!P}$ -immune set, and ⊕P contains a PPPH-immune set. This implies the existence of a ${\rm C\!\!\!\!=\!\!\!P}^B$ 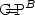-simple set for someoracle B, which extends results of Balcázar et al. [2,4].Our proof technique requires a circuit lower bound for “exactcounting” that is derived from Razborov's [35] circuitlower bound for majority.

In Hoare's (1961) original version of the algorithm  the partitioning element in the central divide-and-conquer step is chosen uniformly at random from the set S in question.Here we consider a variant where this element is the median of a sample of size 2k+1 from S. We investigate convergencein distribution of the number of comparisons required and obtain a simple explicit result for the limitingaverage performance of the median-of-three version.

Communication complexity of two-party (multiparty)protocols has established itself as a successful method for proving lower bounds on the complexity of concrete problems for numerous computing models. While the relations between communication complexity and oblivious, semilective computations are usually transparent and the main difficulty is reduced to proving nontrivial lower bounds on the communication complexity of given computing problems, the situation essentially changes, if one considers non-oblivious or multilective computations. The known lower bound proofs for such computations are far from being transparent and the crucial ideas of these proofs are often hidden behind some nontrivial combinatorial analysis. The aim of this paper is to create a general framework for the use of two-party communication protocols for lower bound proofs on multilective computations. The result of this creation is not only a transparent presentation of some known lower bounds on the complexity of multilective computations on distinct computing models, but also the derivation of new nontrivial lower bounds on multilective VLSI circuits and multilective planar Boolean circuits.In the case of VLSI circuits we obtain a generalization ofThompson's lower bounds on AT 2 complexity for multilective circuits.The Ω(n 2) lower bound on the number of gates of any k-multilectiveplanar Boolean circuit computing a specific Boolean function of n variablesis established for $k<\frac{1}{2} \log_2 n$ . Another advantage of this framework is that it provides lower bounds for a lot of concrete functions. This contrasts to the typical papersdevoted to lower bound proofs, where one establishes a lower bound for one or a few specific functions.