Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T22:28:03.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Immunity and Simplicity for Exact Counting and Other CountingClasses

Published online by Cambridge University Press:  15 August 2002

J. Rothe
J. Rothe*
Affiliation:
Institut für Informatik, Friedrich-Schiller-Universität Jena, 07740 Jena, Germany; [email protected].
Get access

Abstract

Ko [26] and Bruschi [11] independently showed that, insome relativized world, PSPACE (in fact, ⊕P) contains a setthat is immune to the polynomial hierarchy (PH). In this paper, westudy and settle the question of relativized separations withimmunity for PH and the counting classes PP, ${\rm C\!\!\!\!=\!\!\!P}$ , and ⊕Pin all possible pairwise combinations. Our main result is that thereis an oracle A relative to which ${\rm C\!\!\!\!=\!\!\!P}$ contains a set that is immune BPP⊕P.In particular, this ${\rm C\!\!\!\!=\!\!\!P}^A$ set is immune to PHA and to ⊕PA. Strengthening results ofTorán [48] and Green [18], we also show that, in suitable relativizations, NP contains a ${\rm C\!\!\!\!=\!\!\!P}$ -immune set, and ⊕P contains a PPPH-immune set. This implies the existence of a ${\rm C\!\!\!\!=\!\!\!P}^B$ 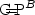-simple set for someoracle B, which extends results of Balcázar et al. [2,4].Our proof technique requires a circuit lower bound for “exactcounting” that is derived from Razborov's [35] circuitlower bound for majority.

Keywords

Computational complexityimmunitycounting classesrelativized computationcircuit lower bounds.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 33 , Issue 2 , March 1999 , pp. 159 - 176
Copyright
© EDP Sciences, 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, T., Gill, J. and Solovay, R., Relativizations of the P=?NP question. SIAM J. Comput. 4 (1975) 431-442. CrossRef
Balcázar, J., Simplicity, relativizations and nondeterminism. SIAM J. Comput. 14 (1985) 148-157. CrossRef
J. Balcázar, J. Díaz and J. Gabarró, Structural Complexity I. EATCS Monographs in theoretical computer science. Springer-Verlag (1988).
J. Balcázar and D. Russo, Immunity and simplicity in relativizations of probabilistic complexity classes. RAIRO, Theoret. Informatics Appl. 22 (1988) 227-244.
Beigel, R., Relativized counting classes: Relations among thresholds, parity, and mods. J. Comput. System Sci. 42 (1991) 76-96. CrossRef
Beigel, R., Perceptrons, PP, and the polynomial hierarchy. Computational Complexity 4 (1994) 339-349. CrossRef
Beigel, R., Chang, R. and Ogiwara, M., A relationship between difference hierarchies and relativized polynomial hierarchies. Math. Systems Theory 26 (1993) 293-310. CrossRef
Bennett, C. and Gill, J., Relative to a random oracle A, ${\rm P}^{A} \neq {\rm NP}^{A} \neq {\rm coNP}^{A}$ with probability 1. SIAM J. Comput. 10 (1981) 96-113. CrossRef
C. Berg and S. Ulfberg, A lower bound for perceptrons and an oracle separation of the PPPH hierarchy. J. Comput. System Sci., to appear. A preliminary version appeared, in Proc. of the 12th Annual IEEE Conference on Computational Complexity, IEEE Computer Society Press (1997) 165-172.
Bovet, D., Crescenzi, P. and Silvestri, R., A uniform approach to define complexity classes. Theoret. Comput. Sci. 104 (1992) 263-283. CrossRef
Bruschi, D., Strong separations of the polynomial hierarchy with oracles: Constructive separations by immune and simple sets. Theoret. Comput. Sci. 102 (1992) 215-252. CrossRef
Bruschi, D., Joseph, D. and Young, P., Strong separations for the boolean hierarchy over RP. Internat. J. Foundations Comput. Sci. 1 (1990) 201-218. CrossRef
Eppstein, D., Hemachandra, L., Tisdall, J. and Yener, B., Simultaneous strong separations of probabilistic and unambiguous complexity classes. Math. Systems Theory 25 (1992) 23-36. CrossRef
L. Fortnow and N. Reingold, PP is closed under truth-table reductions, in Proc. of the 6th Structure in Complexity Theory Conference, IEEE Computer Society Press (1991) 13-15.
Furst, M., Saxe, J. and Sipser, M., Parity, circuits, and the polynomial-time hierarchy. Math. Systems Theory 17 (1984) 13-27. CrossRef
Gill, J., Computational complexity of probabilistic Turing machines. SIAM J. Comput. 6 (1977) 675-695. CrossRef
Goldschlager, L. and Parberry, I., On the construction of parallel computers from various bases of boolean functions. Theoret. Comput. Sci. 43 (1986) 43-58. CrossRef
F. Green, An oracle separating ⊕P from PPPH.Inform. Process. Lett. 37 (1991) 149-153.
T. Gundermann, N. Nasser and G. Wechsung, A survey on counting classes, in Proc. of the 5th Structure in Complexity Theory Conference, IEEE Computer Society Press (1990) 140-153.
J. Håstad, Almost optimal lower bounds for small depth circuits, in S. Micali, Ed., Randomness and Computation 5 of Advances in Computing Research. JAI Press, Greenwich (1989) 143-170.
Hemaspaandra, L., Rothe, J. and Wechsung, G., Easy sets and hard certificate schemes. Acta Inform. 34 (1997) 859-879. CrossRef
Hemaspaandra, L. and Zimand, M., Strong self-reducibility precludes strong immunity. Math. Systems Theory 29 (1996) 535-548. CrossRef
Homer, S. and Maass, W., Oracle dependent properties of the lattice of NP sets. Theoret. Comput. Sci. 24 (1983) 279-289. CrossRef
J. Hopcroft and J. Ullman, Introduction to Automata Theory, Languages, and Computation. Addison-Wesley (1979).
Relativized, K. Ko polynomial time hierarchies having exactly k levels. SIAM J. Comput. 18 (1989) 392-408.
K. Ko, A note on separating the relativized polynomial time hierarchy by immune sets. RAIRO, Theoret. Informatics Appl. 24 (1990) 229-240.
Ladner, R., Lynch, N. and Selman, A., A comparison of polynomial time reducibilities. Theoret. Comput. Sci. 1 (1975) 103-124. CrossRef
Lautemann, C., BPP and the polynomial hierarchy. Inform. Process. Lett. 17 (1983) 215-217. CrossRef
G. Lischke, Towards the actual relationship between NP and exponential time. Mathematical Logic Quarterly, to appear. A preliminary version has appeared as: Impossibilities and possibilities of weak separation between NP and exponential time, in Proc. of the 5th Structure in Complexity Theory Conference, IEEE Computer Society Press (1990) 245-253.
A. Meyer and L. Stockmeyer. The equivalence problem for regular expressions with squaring requires exponential space, in Proc. of the 13th IEEE Symposium on Switching and Automata Theory (1972) 125-129.
Müller, H., A note on balanced immunity. Math. Systems Theory 26 (1993) 157-167. CrossRef
Nisan, N. and Wigderson, A., Hardness vs randomness. J. Comput. System Sci. 49 (1994) 149-167. CrossRef
C. Papadimitriou, Computational Complexity. Addison-Wesley (1994).
Papadimitriou, C. and Zachos, S., Two remarks on the power of counting, in Proc. of the 6th GI Conference on Theoretical Computer Science, Springer-Verlag, Lecture Notes in Computer Science 145 (1983) 269-276. CrossRef
Razborov, A., Lower bounds on the size of bounded depth circuits over a complete basis with logical addition. Mat. Zametki 41 (1987) 598-607. In Russian. English Translation in Mathematical Notes of the Academy of Sciences of the USSR 41 (1987) 333-338.
Regan, K. and Royer, J., On closure properties of bounded two-sided error complexity classes. Math. Systems Theory 28 (1995) 229-243. CrossRef
Rothe, J., Some closure properties of GAP-definable classes. Technical Report TR Math/93/6, Friedrich-Schiller-Universität Jena, Jena, Germany (1993). Appeared as part of: A promise class at least as hard as the polynomial hierarchy. J. Comput. Inform. 1 (1995) 92-107.
J. Rothe, Immunity and simplicity for exact counting and other counting classes. Technical Report TR 679, University of Rochester, Rochester, NY (1998).
Schöning, U. and Book, R., Immunity, relativization, and nondeterminism. SIAM J. Comput. 13 (1984) 329-337. CrossRef
J. Simon, On Some Central Problems in Computational Complexity. PhD thesis, Cornell University, Ithaca, NY (1975). Available as Cornell Department of Computer Science Technical Report TR75-224.
M. Sipser, Borel sets and circuit complexity, in Proc. of the 15th ACM Symposium on Theory of Computing (1983) 61-69.
M. Sipser, A complexity theoretic approach to randomness, in Proc. of the 15th ACM Symposium on Theory of Computing (1983) 330-335.
R. Smolensky. Algebraic methods in the theory of lower bounds for boolean circuit complexity, in Proc. of the 19th ACM Symposium on Theory of Computing, ACM Press (1987) 77-82.
Stockmeyer, L., The polynomial-time hierarchy. Theoret. Comput. Sci. 3 (1977) 1-22. CrossRef
PP, S. Toda is as hard as the polynomial-time hierarchy. SIAM J. Comput. 20 (1991) 865-877.
Toda, S. and Ogiwara, M., Counting classes are at least as hard as the polynomial-time hierarchy. SIAM J. Comput. 21 (1992) 316-328. CrossRef
J. Torán, Structural Properties of the Counting Hierarchies. PhD thesis, Universitat Politècnica de Catalunya, Barcelona (1988).
Torán, J., Complexity classes defined by counting quantifiers. J. Assoc. Comput. Mach. 38 (1991) 753-774. CrossRef
L. Torenvliet, Structural Concepts in Relativised Hierarchies. PhD thesis, Universiteit van Amsterdam, Amsterdam, The Netherlands (1986).
Torenvliet, L. and van Emde Boas, P., Simplicity, immunity, relativizations and nondeterminism. Inform. and Comput. 80 (1989) 1-17. CrossRef
Wagner, K., The complexity of combinatorial problems with succinct input representations. Acta Inform. 23 (1986) 325-356. CrossRef
Wrathall, C., Complete sets and the polynomial-time hierarchy. Theoret. Comput. Sci. 3 (1977) 23-33. CrossRef
A. Yao, Separating the polynomial-time hierarchy by oracles, in Proc. of the 26th IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press (1985) 1-10.