This paper deals with the influence of the Hardy potential in a semilinear heat equation. Precisely, we consider the problem

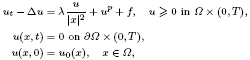
where Ω⊂ℝN, N≥3, is a bounded regular domain such that 0∈Ω, p>1, and u0≥0, f≥0 are in a suitable class of functions.

There is a great difference between this result and the heat equation (λ=0); indeed, if λ>0, there exists a critical exponent p+(λ) such that for p≥p+(λ) there is no solution for any non-trivial initial datum.

The Cauchy problem, Ω=ℝN, is also analysed for 1<p<+(λ). We find the same phenomenon about the critical power p+(λ) as above. Moreover, there exists a Fujita-type exponent, F(λ), in the sense that, independently of the initial datum, for 1<p<F(λ), any solution blows up in a finite time. Moreover, F(λ)>1+2/N, which is the Fujita exponent for the heat equation (λ=0).

This paper is concerned with the existence and nonlinear stability of periodic travelling-wave solutions for a nonlinear Schrödinger-type system arising in nonlinear optics. We show the existence of smooth curves of periodic solutions depending on the dnoidal-type functions. We prove stability results by perturbations having the same minimal wavelength, and instability behaviour by perturbations of two or more times the minimal period. We also establish global well posedness for our system by using Bourgain's approach.

We use spectral sequence techniques to compute centralizers of elements within graded Lie algebras, and the methods are then applied to the calculation of unique normal forms of elements within one-parameter matrix Liealgebras. A finiteness criterion for unique normal forms is presented.

We study incompressible two-dimensional elasticity problems with high-contrast coefficients. The Keller–Dykhne duality relations are extended to the case of Hooke's laws which are equicoercive and uniformly bounded in L1 but not in L∞. A compactness result is obtained for Hooke's laws which are uniformly bounded from above and such that their inverses are bounded in L1 but not in L∞, with a refinement in the periodic case. Moreover, we establish a compactness result in for a sequence of two-dimensional vector-valued functions in which are only bounded in L2.

This article is devoted to the study of the existence of solutions as well as the existence and uniqueness of solutions to a boundary-value problem on the half-line for higher-order nonlinear ordinary differential equations. An existence result is obtained by the use of the Schauder–Tikhonov theorem. Furthermore, an existence and uniqueness criterion is established using the Banach contraction principle. These two results are applied, in particular, to the specific class of higher-order nonlinear ordinary differential equations of Emden–Fowler type and to the special case of higher-order linear ordinary differential equations, respectively. Moreover, some (general or specific) examples demonstrating the applicability of our results are given.

We study the problem of the rigorous derivation of one-dimensional models for a thin curved beam starting from three-dimensional nonlinear elasticity. We describe the limiting models obtained for different scalings of the energy. In particular, we prove that the limit functional corresponding to higher scalings coincides with the one derived by dimension reduction starting from linearized elasticity.

We show how one-dimensional generalized Riccati-type inequalities can be employed to analyse asymptotic behaviour of solutions of elliptic problems. We give Liouville-type theorems as well as necessary conditions for the existence of solutions of specified asymptotic behaviour of nonlinear elliptic problems.

Let f be a transcendental meromorphic function on the complex plane ℂ, let a be a non-zero finite complex number and let n and k be two positive integers. In this paper, we prove that if n≥k+1, then assumes each value b∈ℂ infinitely often. Also, the related normal criterion for families of meromorphic functions is given. Our results generalize the related results of Fang and Zalcman.

We establish an existence theorem for a stationary semiconductor model which takes into account the current generated by the gradient of the temperature.