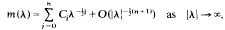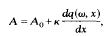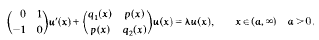Research Article
On a semilinear equation in ℝ2 involving bounded measures
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 181-202
-
- Article
- Export citation
The lattice of congruences on direct products of cyclic semigroups and certain other semigroups
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 203-214
-
- Article
- Export citation
Generation of p-groups by elements of bounded breadth
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 215-221
-
- Article
- Export citation
On the Titchmarsh–Weyl m -function
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 223-237
-
- Article
- Export citation
A description of E-unitary inverse semigroups
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 239-242
-
- Article
- Export citation
Proof of a conjecture of Race
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 243-246
-
- Article
- Export citation
On a class of evolution problems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 247-256
-
- Article
- Export citation
Bounds for the best constant in Landau/s inequality on the line*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 257-262
-
- Article
- Export citation
Estimates for the state density for ordinary differential operators with white gaussian noise potential
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 263-274
-
- Article
- Export citation
On a conjecture related to the number of solutions of a nonlinear Dirichlet problem
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 275-283
-
- Article
- Export citation
The Euler–Maclaurin formula generated by a summation operator
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 285-300
-
- Article
- Export citation
Singularities of dispersion relations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 301-316
-
- Article
- Export citation
Hyperjacobians, determinantal ideals and weak solutions to variational problems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 317-340
-
- Article
- Export citation
Bounds for the eigenvalues of separated Dirac operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 341-366
-
- Article
- Export citation
Index
Index to Volume 95
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. i-ii
-
- Article
- Export citation
Front matter
PRM volume 95 issue 3-4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 95 issue 3-4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b4
-
- Article
-
- You have access
- Export citation