Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:43:00.381Z Has data issue: false hasContentIssue false
  • English
  • Français

XI.—The Free Commutative Entropic Logarithmetic*

Published online by Cambridge University Press:  14 February 2012

H. Minc
Get access Rights & Permissions [Opens in a new window]

Synopsis

The commutative and entropic congruence relations determine a homomorphism on the free logarithmetic 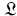, the arithmetic of the indices of powers of the generating element of a free cyclic groupoid. A necessary and sufficient condition that two indices should be concordant (i.e. congruent in the free commutative entropic logarithmetic) is that the bifurcating trees corresponding to these indices should have the same number of free ends at each altitude. It follows that the free commutative entropic logarithmetic can be represented faithfully by index ψ-polynomials (or θ-polynomials) in one indeterminate.

In the concluding section enumeration formulæ are obtained for the number of non-concordant indices of a given altitude and for the number of indices concordant to a given index.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 65 , Issue 2 , 1959 , pp. 177 - 192
Copyright
Copyright © Royal Society of Edinburgh 1959

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Birkhoff, G., 1948. Lattice Theory. New York.Google Scholar
Etherington, I. M. H., 1939. “On non-associative combinations”, Proc. Roy. Soc. Edin., 59, 153–162.CrossRefGoogle Scholar
Etherington, I. M. H., 1940, 1945. “Commutative train algebras of ranks 2 and 3”, J. Lond. Math. Soc., 15, 136–149; 20, 238.Google Scholar
Etherington, I. M. H., 1949. “Non-associative arithmetics”, Proc. Roy. Soc. Edin., A, 62,442–453.Google Scholar
Etherington, I. M. H., 1951. “Non-commutative train algebras of ranks 2 and 3”, Proc. Lond. Math. Soc., 52, 241–252.Google Scholar
Minc, H., 1957. “Index polynomials and bifurcating root-trees”, Proc. Roy. Soc. Edin., A, 64, 319–341.Google Scholar
Murdoch, D. C., 1939. “Quasi-groups which satisfy certain generalized associative laws”, Amer. J. Math., 61, 509–522.CrossRefGoogle Scholar