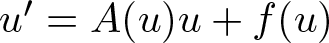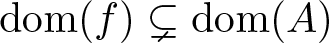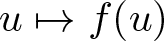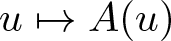1. Introduction
Let E 0 and E 1 be two Banach spaces over 
$\mathbb{K}\in \{\mathbb{R},\mathbb{C}\}$ with continuous and dense embedding
\begin{equation*}
E_1 \stackrel{d}{\hookrightarrow} E_0.
\end{equation*} For each 
$\theta\in (0,1)$, let 
$(\cdot,\cdot)_\theta$ be an arbitrary admissible interpolation functor of exponent θ and denote by 
${E_\theta:= (E_0,E_1)_\theta}$ the corresponding Banach space with norm 
$\|\cdot\|_\theta$. Then
\begin{equation*}
E_1\stackrel{d}{\hookrightarrow} E_\theta\stackrel{d}{\hookrightarrow} E_\vartheta \stackrel{d}{\hookrightarrow} E_0\,,\qquad 0\leqslant \vartheta\leqslant \theta\leqslant 1.
\end{equation*}In this paper, we shall focus our attention on quasilinear parabolic problems
\begin{equation}
u'=A(u)u+f(u)\,,\quad t \gt 0\,,\qquad u(0)=u^0.
\end{equation}Here, we assume for the quasilinear part
\begin{equation}
A\in C^{1-}\big(O_\beta,\mathcal{H}(E_1,E_0) \big),
\end{equation}where
\begin{equation}
\beta\in [0,1)\quad \text{and }\quad \emptyset\not= O_\beta\, \text{is an open subset of } E_\beta,
\end{equation} and where 
$\mathcal{H}(E_1,E_0)$ is the open subset of the bounded linear operators 
$\mathcal{L}(E_1,E_0)$ consisting of generators of strongly continuous analytic semigroups on E 0. Moreover, for the semilinear part we assume that there are numbers
\begin{equation}0 \lt \gamma \lt 1\,,\qquad \beta\leqslant \xi \lt 1\,, \qquad q\geqslant 1,\end{equation} with the property that 
$f:O_\xi\to E_\gamma$ is locally Lipschitz continuous on the open subset 
$O_\xi:=O_\beta\cap E_\xi$ of Eξ in the sense that for each R > 0 there is 
$c(R) \gt 0$ such that, for all 
$w,\,v\in O_\xi\cap \bar{\mathbb{B}}_{E_\beta}(0,R)$,
\begin{equation}
\begin{aligned}
&\|f(w)-f(v)\|_{\gamma}\\
&\leqslant c(R)\big[1+\|w\|_{\xi}^{q-1}+\|v\|_{\xi}^{q-1}\big]\big[\big(1+\|w\|_{\xi}+\|v\|_{\xi}\big) \|w-v\|_{\beta}+\|w-v\|_{\xi}\big].
\end{aligned}
\end{equation}As for the initial value we fix
\begin{equation}
\alpha\in (\beta,1) \quad \text{with }\quad (\xi-\alpha)q \lt \min\{1,1+\gamma-\alpha\}.
\end{equation} Under assumptions (1.2) we shall prove that, for any 
$u^0\in O_\alpha:=O_\beta\cap E_\alpha$, problem (1.1) is well-posed and in fact generates a semiflow on Oα. Note that (1.2d) includes in particular the case when, for all 
$w,\,v\in O_\xi\cap \bar{\mathbb{B}}_{E_\beta}(0,R)$,
\begin{equation}
\|f(w)-f(v)\|_{\gamma}\leqslant c(R)\big(1+\|w\|_{\xi}^{q-1}+\|v\|_{\xi}^{q-1}\big)\|w-v\|_{\xi},
\end{equation} and that (1.2e) is satisfied if 
$\alpha\in (\xi,1)$. The local Lipshitz continuity property (1.2d) and its stronger version (1.3) appear quite naturally in applications, see lemma 4.1 and the examples in 
$\S$5 and 
$\S$6. Once E 0 and E 1 are fixed, the parameters β and ξ are chosen minimally such that A and f are well-defined on the corresponding spaces (with a preferably large parameter γ for the target space of f). The range of the parameter α defining the regularity of the initial value is then determined by (1.2e). The parameter 
$q\geqslant1$ in (1.2d) and (1.3) measures the growth of the nonlinearity f with respect to the Eξ-terms (while Eβ-terms can be absorbed into the constant c(R)).
Of course, well-posedness of quasilinear and even fully nonlinear equations is well-established, see e.g. [Reference Amann4, Reference Amann7, Reference Clément and Li13, Reference Clément and Simonett14, Reference Guidetti18, Reference Lunardi25–Reference Lunardi27, Reference Matioc and Walker30–Reference Prüss, Simonett and Wilke33] for the former and e.g. [Reference Acquistapace and Terreni1, Reference Angenent11, Reference Da Prato15–Reference Da Prato and Lunardi17, Reference Lunardi28, Reference Lunardi29] for the latter problems. In particular, a general result on existence of solutions to (1.1) is stated in [Reference Amann7, theorem 12.1] (and established in [Reference Amann4], see also [Reference Matioc and Walker30]) for the case that the nonlinearities A and f are defined and Lipschitz continuous on the same set Oβ. More precisely, it is proven therein that if
\begin{equation*}
(A,f)\in C^{1-}\big(O_\beta,\mathcal{H}(E_1,E_0)\times E_\gamma\big)\,,\qquad u^0\in O_\alpha\,,\qquad 0 \lt \gamma\leqslant \beta \lt \alpha \lt 1,
\end{equation*} (which is a special case of (1.2) taking q = 1 and 
$\xi=\beta \lt \alpha$), then problem (1.1) has a unique maximal strong solution
\begin{equation*}
\begin{aligned}
u=u(\cdot;u^0)&\in C^1((0,t^+(u^0)),E_0)\cap C((0,t^+(u^0)),E_1)\cap C ([0,t^+(u^0)),O_\alpha)\\
&\quad\cap C^{\alpha-\theta}\big([0,t^+(u^0)), E_\theta\big)
\end{aligned}
\end{equation*} for 
$\theta\in [0,\alpha]$. Moreover, the mapping 
$(t,u^0)\mapsto u(t;u^0)$ is a semiflow on Oα, and therefore 
$t^+(u^0)=\infty$ if the corresponding orbit is relatively compact in Oα.
Herein we shall prove with theorem 1.1 below a similar result to [Reference Amann7, theorem 12.1] (see also [Reference Amann4]) for problem (1.1), but under the more general assumptions (1.2). In particular, theorem 1.1 addresses the new case when 
${\beta \lt \alpha \lt \xi}$ in (1.2). Note that then 
$E_\xi\hookrightarrow E_\alpha\hookrightarrow E_\beta$ and hence, the semilinear part f, being defined on Oξ, needs not be defined on the phase space Eα and requires possibly more regularity than the quasilinear part A. It is worth emphasizing that also for this case we establish that problem (1.1) induces a semiflow on Oα so that relatively compact orbits in Oα are global. The global existence criterion can thus be stated in weaker norms than e.g. in [Reference Amann7].
For the proof, we rely on regularizing effects for quasilinear parabolic equations and work in time-weighted spaces 
$C_\mu((0,T],E_\xi)$ of continuous maps 
${v:(0,T]\to E_\xi}$ satisfying 
$\lim_{t\to 0}t^\mu\|v(t)\|_\xi=0$, where T > 0 and 
$\mu \gt (\xi-\alpha)_+$. Given 
$x\in\mathbb{R}$, we set 
$x_+:=\max\{0,\,x\}$.
Time-weighted spaces were used previously for quasilinear evolution problems in the context of maximal regularity in [Reference Angenent11, Reference Clément and Simonett14] and later in [Reference Köhne, Prüss and Wilke20, Reference LeCrone, Prüss and Wilke23, Reference Prüss and Simonett32, Reference Prüss and Wilke34]. In particular, well-posedness of (1.1) is established in [Reference LeCrone, Prüss and Wilke23] in time-weighted Lp-spaces assuming that f satisfies (in the simplest case) (1.3) along with inequality (1.2e) for γ = 0 in the scale of real interpolation spaces and assuming that the operator A(u) has the property of maximal Lp-regularity for 
${u\in O_\alpha}$ (see [Reference Prüss, Simonett and Wilke33, Reference Prüss and Wilke34] for an improvement with equality in (1.2e) under an additional structural condition on the Banach spaces E 0 and E 1). Furthermore, we refer to [Reference LeCrone and Simonett24] for a result in the same spirit based on the concept of continuous maximal regularity in time-weighted spaces and assuming (1.3) with inequality (1.2e) in the scale of continuous interpolation spaces. Theorem 1.1 below is a comparable result outside the setting of maximal regularity and for arbitrary (admissible) interpolation functors under the more general version (1.2d) of (1.3).
Finally, we point out that, in order to impose weaker conditions on the initial values, time-weighted spaces 
$C_\mu(0,T],E)$ (with suitable Banach spaces E) were used for concrete semilinear problems (see (1.6) below) with bilinear right-hand sides (i.e. q = 2 in (1.3)) even before [Reference Amann9, Reference Amann and Walker10, Reference Walker and Webb37] and recently [Reference Laurençot and Walker22]. Theorem 1.2 below provides a general result for this case, thereby sharpening the result for the quasilinear problem.
Our first main result is theorem 1.1 and establishes the well-posedness of the quasilinear evolution problem (1.1) restricted to the assumptions (1.2).
Theorem 1.1 Suppose (1.2).
(i) (Existence) Given any
$u^0\in O_\alpha$, the Cauchy problem (1.1) possesses a maximal strong solution
\begin{equation*}
\begin{aligned}
u(\cdot;u^0)&\in C^1\big((0,t^+(u^0)),E_0\big)\cap C\big((0,t^+(u^0)),E_1\big)\cap C \big([0,t^+(u^0)),O_\alpha\big)
\end{aligned}
\end{equation*}with
$ t^+(u^0)\in(0,\infty]$. Moreover,
\begin{align*}
u(\cdot;u^0)\in C^{\min\{\alpha-\theta,\,(1-\mu q)_+\}}\big([0, T], E_\theta\big)\cap C_{\mu}\big((0,T], E_\xi\big)
\end{align*}for all
$T \lt t^+(u^0)$, where $\theta\in [0,\alpha]$ and $\mu \gt (\xi-\alpha)_+$.(ii) (Uniqueness) If
\begin{equation*}\tilde u \in C^1\big((0,T],E_0\big)\cap C\big((0,T],E_1\big)\cap C^\vartheta \big([0,T],O_\beta\big) \cap C_\nu\big((0,T],E_\xi\big)\end{equation*}is a solution to (1.1) for some T > 0,
$\vartheta\in(0,1)$, and $\nu\geqslant 0$ with
\begin{align*}
q\nu \lt \min\{1,1+\gamma-\alpha\},
\end{align*}then
$T \lt t^+(u^0)$ and $\tilde u=u(\cdot;u^0)$ on $[0,T].$(iii) (Continuous dependence) The map
$(t,u^0)\mapsto u(t;u^0)$ is a semiflow on Oα.(iv) (Global existence) If the orbit
$u([0,t^+(u^0));u^0)$ is relatively compact in Oα, then ${t^+(u^0)=\infty}$.(v) (Blow-up criterion) Let
$u^0\in O_\alpha$ be such that $t^+(u^0) \lt \infty$.(a) If
$u(\cdot;u^0):[0,t^+(u^0))\to E_\alpha$ is uniformly continuous, then
(1.4)\begin{equation}
\lim_{t\nearrow t^+(u^0)}\mathrm{dist}_{E_\alpha}\big( u(t;u^0),\partial O_\alpha\big)=0.
\end{equation}(b) If E 1 is compactly embedded in E 0, then
(1.5)\begin{equation}
\lim_{t\nearrow t^+(u^0)}\|u(t;u^0)\|_{\theta}=\infty\quad\text{or }\quad \lim_{t\nearrow t^+(u^0)}\mathrm{dist}_{E_\beta}\big( u([0,t];u^0),\partial O_\beta\big)=0
\end{equation}for each
$\theta\in (\beta,1)$ with $(\xi-\theta)q \lt \min\{1,1+\gamma-\theta\}$.
Criterion (iv) yields global existence when the orbit is relatively compact in Eα. In particular, if E 1 embeds compactly in E 0, then a priori estimates on the solution in Eα are sufficient for global existence as noted in condition (1.5) (in contrast e.g. to [Reference Amann7] where estimates in Eξ would be needed for the same conclusion).
The proof of theorem 1.1 relies on a classical fixed point argument. However, the technical details do not seem to be completely straightforward due to the singularity of 
$t\mapsto f(u(t))$ at t = 0 which has to be monitored carefully.
Semilinear parabolic problems
Of course, the result for the quasilinear case remains true for semilinear parabolic equations
\begin{equation*}
u'=Au+f(u)\,,\quad t \gt 0\,,\qquad u(0)=u^0,
\end{equation*}or, more generally, for parabolic evolution equations
\begin{equation}
u'=A(t)u+f(u)\,,\quad t \gt 0\,,\qquad u(0)=u^0,
\end{equation} with time-dependent operators 
$A=A(t)$. In this setting theorem 1.1 can be sharpened though. We present with theorem 1.2 below a result for the particular case that f is defined on the whole interpolation space Eξ. More precisely, let
\begin{equation}
A\in C^\rho(\mathbb{R}^+,\mathcal{H}(E_1,E_0))
\end{equation}for some ρ > 0 and let
\begin{equation}
\begin{aligned}
&0\leqslant \alpha\leqslant \xi\leqslant 1\,,\quad 0\leqslant \gamma \lt 1\,,\quad (\gamma,\xi)\not= (0,1)\,,\\
&q\geqslant 1\,,\quad (\xi-\alpha)q \lt \min\{1,1+\gamma-\alpha\}.
\end{aligned}
\end{equation} Assume that the map 
$f:E_\xi\to E_\gamma$ is locally Lipschitz continuous in the sense that for each R > 0 there is a constant 
${c(R) \gt 0}$ such that
\begin{equation}
\begin{aligned}
&\|f(w)-f(v)\|_{\gamma}\\
&\leqslant c(R)\big[1+\|w\|_{\xi}^{q-1}+\|v\|_{\xi}^{q-1}\big]\big[\big(1+\|w\|_{\xi}+\|v\|_{\xi}\big) \|w-v\|_{{\alpha}}+\|w-v\|_{\xi}\big]
\end{aligned}
\end{equation} for all 
$w,\,v\in E_\xi\cap \bar{\mathbb{B}}_{E_{\alpha}}(0,R)$.
It is worth pointing out that we may choose the phase space of the evolution as well as the target space of the semilinearity f as E 0 (that is, we may set 
$\alpha=\gamma=0$) and that the nonlinearity f(u) need not be defined on the phase space Eα; see also remark 2.2 below for more details. The well-posedness result regarding the semilinear problem (1.6) under assumption (1.7) reads as follows:
Theorem 1.2 Suppose (1.7).
(i) (Existence) Given any
$u^0\in E_\alpha$, the Cauchy problem (1.6) possesses a maximal strong solution
\begin{equation*}
\begin{aligned}
u(\cdot;u^0)&\in C^1\big((0,t^+(u^0)),E_0\big)\cap C\big((0,t^+(u^0)),E_1\big)\cap C \big([0,t^+(u^0)),E_\alpha\big)
\end{aligned}
\end{equation*}with
$ t^+(u^0)\in(0,\infty]$. Moreover,
\begin{equation*}
u(\cdot;u^0)\in C^{\min\{\alpha-\theta,\,(1-\mu q)_+\}}\big([0,T], E_\theta\big)\cap C_{\mu}\big((0,T], E_\xi\big)
\end{equation*}for all
$\theta\in [0,\alpha]$, $\mu \gt \xi-\alpha$, and $T \lt t^+(u^0)$.(ii) (Blow-up criterion) If
$u^0\in E_\alpha$ is such that $t^+(u^0) \lt \infty$, then
(1.8)\begin{equation}
\underset{t\nearrow t^+(u^0)}\limsup\|u(t;u^0)\|_{\alpha}=\infty.
\end{equation}(iii) (Uniqueness) If
\begin{equation*}\tilde u \in C^1\big((0,T],E_0\big)\cap C\big((0,T],E_1\big)\cap C \big([0,T],E_{\alpha}\big) \cap C_\nu\big((0,T],E_\xi\big)\end{equation*}is a solution to (1.6) for some T > 0 and
$\nu\geqslant 0$ with $q\nu \lt \min\{1,1+\gamma-\alpha\}$, then $T \lt t^+(u^0)$ and $\tilde u=u(\cdot;u^0)$ on $[0,T].$
Moreover, if 
$A(t)=A\in \mathcal{H}(E_1,E_0)$ for all 
$t\geqslant 0$, then:
(iv) (Continuous dependence) The map
$(t,u^0)\mapsto u(t;u^0)$ is a semiflow on Eα.(v) (Global existence) If the orbit
$u([0,t^+(u^0));u^0)$ is relatively compact in Eα, then ${t^+(u^0)=\infty}$.
Note that an priori bound in Eα already ensures that the solution is globally defined even in the case of a non-compact embedding 
${E_1\hookrightarrow E_0}$.
The proof of theorem 1.1 is presented in 
$\S$2, while the proof of theorem 1.2 is established in 
$\S$3.To prepare applications of these results we state some auxiliary results in 
$\S$4. In the subsequent 
$\S$5 and 
$\S$6we will then provide some applications of theorems 1.1 and 1.2 to certain chemotaxis systems featuring cross-diffusion terms, in particular with focus on the global existence criterion.
2. Proof of theorem 1.1
The proof of theorem 1.1 is based on proposition 2.1 below. Before we address the latter result, let us first recall some basic facts used in the proofs.
Preliminaries
Let T > 0, 
$\mu\in \mathbb{R}$, and consider a Banach space E. We denote by 
$C_{\mu}((0,T],E)$ the Banach space of all functions 
$u\in C((0,T],E)$ such that 
$t^{\mu} u(t)\rightarrow 0$ in E as 
$t\rightarrow 0$, equipped with the norm
\begin{equation*}
u\mapsto \|u\|_{C_{\mu}((0,T],E)} := \sup\left\{t^{\mu}\, \|u(t)\|_E \,:\, t\in (0,T]\right\}.
\end{equation*}Note that
\begin{equation}
C_{\mu}((0,T],E)\hookrightarrow C_{\nu}((0,T],E)\,,\quad \mu\leqslant \nu.
\end{equation} Given ω > 0 and 
$\kappa\geqslant 1$, we denote by 
${\mathcal{H}(E_1,E_0;\kappa,\omega)}$ the class of all bounded operators 
$\mathcal{A}\in\mathcal{L}(E_1,E_0)$ such that 
$\omega-\mathcal{A}$ is an isomorphism from E 1 onto E 0 and
\begin{equation*}
\frac{1}{\kappa}\,\leqslant\,\frac{\|(\mu-\mathcal{A})z\|_{0}}{\vert\mu\vert \,\| z\|_{0}+\|z\|_{1}}\,\leqslant \, \kappa\ ,\qquad {\mathrm{Re}\,}
\mu\geqslant \omega\ ,\quad z\in E_1\setminus\{0\}.
\end{equation*}Then
\begin{equation*}\mathcal{H}(E_1,E_0)=\bigcup_{\omega \gt 0\,,\,\kappa\geqslant 1} \mathcal{H}(E_1,E_0;\kappa,\omega).\end{equation*} For time-dependent operators 
$\mathcal{A}\in C^\rho(I,\mathcal{H}(E_1,E_0))$ with 
$\rho\in(0,1)$ there exists a unique parabolic evolution operator 
$U_\mathcal{A}(t,s)$, 
$0\leqslant s\leqslant t \lt \sup I$, in the sense of [Reference Amann8, II. section 2].
Based on this, we may reformulate the quasilinear Cauchy problem (1.1) as a fixed point equation of the form
\begin{equation}
u(t)=U_{A(u)}(t,0)u^0+ \int_0^t U_{A(u)}(t,\tau) f(u(\tau))\,\mathrm{d} \tau\,,\quad t \gt 0,
\end{equation}see the proof below of proposition 2.1.
Proposition 2.1. Suppose (1.2). Let 
$S_\alpha \subset O_\alpha$ be a compact subset of Eα. Then, there exist a neighbourhood Qα of Sα in Oα and 
${T:=T(S_\alpha) \gt 0}$ such that, for each 
${u^0\in Q_\alpha}$, the problem (1.1) has a strong solution
\begin{equation}
\begin{aligned}
u=u(\cdot;u^0)\in &\ C^1\big((0,T],E_0\big)\cap C\big((0,T],E_1\big)\cap C \big([0,T],O_\alpha\big) \\
&\, \cap C^{\min\{\alpha-\theta,\,(1-\mu q)_+\}}\big([0,T], E_\theta\big)\cap C_\mu\big((0,T],E_\xi\big)
\end{aligned}
\end{equation} for any 
$\theta\in [0,\alpha]$ and 
$\mu \gt (\xi-\alpha)_+$. Moreover, there is a constant 
$c_0:=c_0(S_\alpha) \gt 0$ such that
\begin{equation*}
\| u(t;u^0)-u(t;u^1)\|_\alpha\leqslant c_0 \| u^0-u^1\|_\alpha\,,\qquad 0\leqslant t\leqslant T\,,\quad u^0, u^1\in Q_\alpha.
\end{equation*}Finally, if
\begin{equation}
\tilde u\in C^1((0,T],E_0)\cap C((0,T],E_1)\cap C^\vartheta ([0,T],O_\beta) \cap C_\nu\big((0,T],E_\xi\big)
\end{equation} with 
$ \vartheta\in(0,1)$ and 
$0\leqslant q\nu \lt \min \{1, 1+\gamma-\alpha \}$ is a solution to problem (1.1) satsfying 
${\tilde u (0)=u^0 \in Q_\alpha}$, then 
$\tilde u=u(\cdot;u^0)$.
Proof. We devise the proof into several steps.
The fixed point formulation. Since 
$S_\alpha \subset O_\alpha$ is compact in Eα and since Eα embeds continuously into Eβ, we find a constant δ > 0 such that 
$\mathrm{dist}_{E_\beta}(S_\alpha, \partial O_\beta) \gt 2\delta \gt 0$. Moreover, due to (1.2a) and [Reference Amann2, II. proposition 6.4], A is uniformly Lipschitz continuous on some neighbourhood of Sα, hence there are ɛ > 0 and L > 0 such that
\begin{equation*}
\bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon)
\subset \mathbb{B}_{E_\beta}(S_\alpha, \delta) \subset O_\beta
\end{equation*}and
\begin{equation}
\|A(x) - A(y)\|_{\mathcal{L}(E_1,E_0)} \leqslant L\|x-y\|_\beta\ , \quad x,y \in
\bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon).
\end{equation} The compactness of 
$A(S_\alpha)$ in 
$\mathcal{H}(E_1,E_0)$ implies according to [Reference Amann8, I. corollary 1.3.2] that there are 
${\kappa\geqslant 1}$ and ω > 0 such that (making ɛ > 0 smaller, if necessary)
\begin{equation}
A(x)\in \mathcal{H}(E_1,E_0;\kappa,\omega)\,,\quad x \in \bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon).
\end{equation} Recalling (1.2e) and (2.1), we may choose 
$\alpha_0\in (\beta,\alpha)$ if 
$\alpha \lt \xi$ respectively put 
${\alpha_0:=\xi}$ if 
$\alpha\geqslant \xi$, choose 
$\gamma_0\in (0,\gamma)$, and assume that µ satisfies
\begin{equation}
\xi-\alpha_0 \lt \mu \lt \min\left\{\frac{1}{q},\frac{1+\gamma_0-\alpha}{q}\right\}.
\end{equation} Fix 
$\rho\in (0,\min\{\alpha-\beta,1-\mu q\})$. Given 
$T \in (0,1)$ (chosen small enough as specified later on), define a closed subset of 
$C([0,T], E_\beta)$ by
\begin{equation*}
\mathcal{V}_T := \left\{v \in C([0,T], E_\beta) \,:\,\begin{array}{l}
\|v(t) - v(s)\|_\beta \leqslant |t-s|^{\rho}\ \mathrm{and}\ v(t)\in \bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon)\\ \textrm{for all}\ 0 \leqslant s,t \leqslant T
\end{array}\right\}.
\end{equation*} Hence, if 
$v\in\mathcal{V}_T$, then (2.6) ensures
\begin{equation}
A(v(t))\in \mathcal{H}(E_1,E_0;\kappa,\omega)\,,\quad t\in [0,T],
\end{equation}while (2.5) implies
\begin{equation}
A(v)\in C^\rho\big([0,T],\mathcal{L}(E_1,E_0)\big)\quad\text{with}\quad \sup_{0\leqslant s \lt t\leqslant T}
\frac{\| A(v(t))- A(v(s))\|_{\mathcal{L}(E_1,E_0)}}{( t-s)^\rho}\leqslant L.
\end{equation} For each 
$v\in\mathcal{V}_T$, the evolution operator
\begin{equation*}
U_{A(v)}(t,s)\,,\quad 0\leqslant s\leqslant t\leqslant T,
\end{equation*} is thus well-defined and (2.8) guarantees that we are in a position to use the results of [Reference Amann8, II. section 5]. In particular, due to [Reference Amann8, II.lemma 5.1.3] there exists 
$c=c(S_\alpha) \gt 0$ such that
\begin{equation}
\|U_{A(v)}(t,s)\|_{\mathcal{L}(E_\theta)}+(t-s)^{\theta-\vartheta_0}\,\|U_{A(v)}(t,s)\|_{\mathcal{L}(E_\vartheta,E_\theta)} \leqslant c \,, \quad 0\leqslant s\leqslant t\leqslant T,
\end{equation} for 
$0\leqslant \vartheta_0\leqslant \vartheta\leqslant \theta\leqslant 1$ with 
$\vartheta_0 \lt \vartheta$ if 
$0 \lt \vartheta \lt \theta \lt 1$. In the following, 
${c=c(S_\alpha)}$ denotes positive constants depending only on Sα and 
${\alpha,\, \beta,\, \gamma,\, \xi,\, \mu,\alpha_0,\, \gamma_0, \,\varepsilon,\, \delta}$, but neither on 
$v\in\mathcal{V}_T$ nor on 
${T\in (0,1)}$.
We introduce the complete metric space
\begin{equation*}
\mathcal{W}_T:=\mathcal{V}_T\cap \bar{\mathbb{B}}_{C_\mu((0,T],E_\xi)}(0,1)
\end{equation*}equipped with the metric
\begin{equation*}
d_{\mathcal{W}_T}(u,v):=\|u-v\|_{C([0,T],E_\beta)}+\|u-v\|_{C_\mu((0,T],E_\xi)}\,,\quad u,v\in \mathcal{W}_T.
\end{equation*} Let 
$u,v\in \mathcal{W}_T$. Note that 
$u(t)\in \bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon) \subset O_\beta$ for 
$t\in [0,T]$, while 
$u(t)\in E_\xi$ for 
$t\in (0,T]$. In particular, 
$u(t)\in O_\xi$ for 
$t\in (0,T]$. Moreover, there is 
$c=c(S_\alpha) \gt 0$ such that 
$\|u(t)\|_\beta\leqslant c$ for 
${t\in [0,T]}$ and 
$\|u(t)\|_\xi \leqslant t^{-\mu}$ for 
$t\in (0,T]$. Fixing 
$v^0\in O_\xi$ arbitrarily, we deduce from (1.2d) that
\begin{align}
\|f(u(t))\|_{\gamma}&\leqslant \|f(u(t))-f(v^0)\|_{\gamma} +\|f(v^0)\|_{\gamma}\leqslant c t^{-\mu q}\,,\quad t\in (0,T],
\end{align} for some constant 
$c=c(S_\alpha) \gt 0$. Also note that, for 
$t\in (0,T]$,
\begin{align}
\|f(u(t))-f(v(t))\|_{\gamma}\leqslant c t^{-\mu q} \|u(t)-v(t)\|_{\beta}+ c t^{-\mu (q-1)} \|u(t)-v(t)\|_{\xi},
\end{align} where again 
$c=c(S_\alpha) \gt 0$. Set
\begin{equation*}
Q_\alpha:=\mathbb{B}_{E_\alpha}(S_\alpha,\varepsilon/(1+e_{\alpha,\beta}))\subset O_\alpha,
\end{equation*} where 
$e_{\alpha,\beta} \gt 0$ is the norm of the embedding 
$E_\alpha\hookrightarrow E_\beta$. Given 
$u^0\in Q_\alpha,$ define
\begin{equation}
F(u)(t):= U_{A(u)}(t,0)u^0 +\int_0^t U_{A(u)}(t,\tau) f(u(\tau))\,\mathrm{d} \tau\,,\quad t\in [0,T]\,,\quad u\in\mathcal{W}_T.
\end{equation} We shall prove that 
$F:\mathcal{W}_T\rightarrow \mathcal{W}_T$ is a contraction for 
$T=T(S_\alpha)\in (0,1)$ small enough. To this end, particular attention has to be paid to the singularity of the function 
$t\mapsto f(u(t))$ at t = 0 when studying the function F(u).
Continuity in Eβ. To prove the continuity in Eβ we note that, for 
$0\leqslant s \lt t\leqslant T$, 
$u\in\mathcal{W}_T$, and 
$\theta\in[0,\alpha]$,
\begin{align}
\|F(u)(t)-F(u)(s)\|_\theta&\leqslant \|U_{A(u)}(t,0)u^0-U_{A(u)}(s,0)u^0\|_{\theta} \nonumber\\
&\quad+\int_0^s \|U_{A(u)}(t,\tau)-U_{A(u)}(s,\tau)\|_{\mathcal{L}(E_\gamma,E_\theta)} \,\|{f(u(\tau))}\|_\gamma\,\mathrm{d} \tau \nonumber\\
&\quad +\int_s^t \|U_{A(u)}(t,\tau)\|_{\mathcal{L}(E_\gamma,E_\theta)} \,\|{f(u(\tau))}\|_\gamma\,\mathrm{d} \tau=:I_1+I_2+I_3.
\end{align} We first note from (2.8) and [Reference Amann8, II. theorem 5.3.1] (with f = 0 therein) that there exists 
$c=c(S_\alpha) \gt 0$ with
\begin{align}
I_1 \leqslant c (t-s)^{\alpha-\theta} \|u^0\|_\alpha.
\end{align}Moreover, since
\begin{equation*}
\|U_{A(u)}(t,s)-1\|_{\mathcal{L}(E_\alpha,E_\theta)}\leqslant c(t-s)^{\alpha-\theta},
\end{equation*}due to [Reference Amann8, II. theorem 5.3.1] and (2.8), we use (2.9) and (2.10) to derive
\begin{align}
I_2 &\leqslant \int_0^s \|U_{A(u)}(t,s)-1\|_{\mathcal{L}(E_\alpha,E_\theta)} \,\|U_{A(u)}(s,\tau)\|_{\mathcal{L}(E_\gamma,E_\alpha)} \|f(u(\tau))\|_\gamma\,\mathrm{d} \tau\nonumber\\
&\leqslant c (t-s)^{\alpha-\theta}\,\max\Big\{\int_0^s (s-\tau)^{\gamma_0-\alpha} \tau ^{-\mu q}\,\mathrm{d} \tau,\, \int_0^s \tau ^{-\mu q}\,\mathrm{d} \tau\Big\}\nonumber\\
&\leqslant c\,\max\{T^{1+\gamma_0-\alpha-\mu q},\,T^{1-\mu q}\}\, (t-s)^{\alpha-\theta},
\end{align}since
\begin{align*}
\int_0^s (s-\tau)^{\gamma_0-\alpha} \tau ^{-\mu q}\,\mathrm{d} \tau&=s^{1+\gamma_0-\alpha-\mu q}\int_0^1 (1-\tau)^{\gamma_0-\alpha} \tau ^{-\mu q}\,\mathrm{d} \tau\\
&\leqslant T^{1+\gamma_0-\alpha-\mu q} \mathsf{B}(1+\gamma_0-\alpha,1-\mu q),
\end{align*} where 
$\mathsf{B}$ denotes the Beta function. Using again (2.9) with (2.10), we obtain similarly
\begin{align}
I_3 &\leqslant c\max\Big\{\int_s^t (t-\tau)^{\gamma_0-\theta} \,\tau^{-\mu q}\,\mathrm{d} \tau,\, \int_s^t \tau^{-\mu q}\,\mathrm{d} \tau\Big\} \nonumber\\
&\leqslant c\max \big\{(t-s)^{1+\gamma_0-\alpha-\mu q}(t-s)^{\alpha-\theta},\,(t-s)^{1-\mu q}\big\}.
\end{align} Due to (2.7) and 
$\rho\in (0,\min\{\alpha-\beta,1-\mu q\})$, we see from (2.13) with 
$\theta=\beta$ that we may choose the constant 
${T=T(S_\alpha)\in (0,1)}$ small enough to get
\begin{align}
\|F(u)(t)-F(u)(s)\|_\beta &\leqslant (t-s)^{\rho}\,,\quad 0\leqslant s\leqslant t\leqslant T,
\end{align} and, since 
$F(u)(0)=u^0$,
\begin{equation*}
\begin{split}
\|F(u)(t)-u^0\|_\beta &\leqslant T^{\rho}\leqslant \varepsilon\,,\quad 0\leqslant t\leqslant T.
\end{split}
\end{equation*} In particular, we infer from 
$u^0\in Q_\alpha=\mathbb{B}_{E_\alpha}(S_\alpha,\varepsilon/(1+e_{\alpha,\beta}))$ that
\begin{align}
F(u)(t)\in \bar{\mathbb{B}}_{E_\beta}(S_\alpha, 2\varepsilon)\,,\quad 0\leqslant t\leqslant T,
\end{align} hence 
$F(u)\in\mathcal{V}_T.$
Continuity in Eξ. We now prove that 
$F(u)\in C((0,T], E_1)$, which in particular implies 
$F(u)\in C((0,T], E_\xi)$. To this end we fix 
$\varepsilon\in (0,T)$ and set 
$u_\varepsilon(t):=u(t+\varepsilon)$ for 
$t\in [0,T-\varepsilon]$. Then, in view of (2.2) we have 
$u_\varepsilon\in C([0,T-\varepsilon],E_\xi)$ and (1.2d) entails that 
$f(u_\varepsilon)\in C([0,T-\varepsilon],E_\gamma)$. If
\begin{align*}
U_{A(u_\varepsilon)}(t,s)=U_{A(u)}(t+\varepsilon,s+\varepsilon)\,,\quad 0\leqslant s\leqslant t\leqslant T-\varepsilon,
\end{align*} denotes the evolution operator associated with 
$A(u_\varepsilon)$, we infer from the definition of F(u) that
\begin{equation}
F(u)(t+\varepsilon)=U_{A(u_\varepsilon)}(t,0)F(u)(\varepsilon)+\int_0^t U_{A(u_\varepsilon)}(t,s) f(u_\varepsilon(s))\,\mathrm{d} s\,,\quad t\in [0,T-\varepsilon].
\end{equation}Applying [Reference Amann8, II. theorem 1.2.2, II. remarks 2.1.2 (e)], yields
\begin{equation*}F(u)( \varepsilon+\cdot) \in C\big((0,T-\varepsilon],E_1\big)\cap C^1\big((0,T-\varepsilon],E_0\big)\end{equation*} for all 
$\varepsilon\in(0,T)$, hence
\begin{equation}
F(u)\in C\big((0,T],E_1\big)\cap C^1\big((0,T],E_0\big).
\end{equation}Similarly, we derive from (2.9), (2.10), and the definition of α 0 that
\begin{align*}
\|F(u)(t)\|_\xi &\leqslant \|U_{A(u)}(t,0)\|_{\mathcal{L}(E_\alpha,E_\xi)}\, \|u^0\|_{\alpha}+\int_0^t \|U_{A(u)}(t,\tau)\|_{\mathcal{L}(E_\gamma,E_\xi)} \,\|f(u(\tau))\|_\gamma\,\mathrm{d} \tau\\
&\leqslant c\big( t^{\alpha_0-\xi} + \max\big\{t^{1+\gamma_0-\xi -\mu q},\, t^{1-\mu q}\big\}\big),
\end{align*} for 
$t\in (0,T]$, hence
\begin{align}
t^\mu \|F(u)(t)\|_\xi &\leqslant c\big( t^{\alpha_0-\xi+\mu} + \max\big\{t^{1+\gamma_0-\xi -\mu( q-1)},\, t^{1-\mu q}\}\big)\,,\quad t\in (0,T].
\end{align} Owing to (2.7) (noticing that 
$\xi +\mu(q-1) \lt \mu q+\alpha \lt 1+\gamma_0$) we may make the constant 
$T=T(S_\alpha)\in (0,1)$ smaller, if necessary, to obtain
\begin{align}
\|F(u)\|_{C_\mu((0,T],E_\xi)} &\leqslant 1.
\end{align} It now follows from the relations (2.14), (2.15), and (2.19) that 
$F:\mathcal{W}_T \to \mathcal{W}_T$ provided that 
$T=T(S_\alpha)\in (0,1)$ is small enough.
The contraction property. It remains to show that F is a contraction. To this end, let 
$u,v\in \mathcal{W}_T$ and observe from [Reference Amann8, II. lemma 5.1.4], (2.8), and (2.5) that there is a constant 
$c=c(S_\alpha) \gt 0$ such that, for 
$0\leqslant \tau \lt t\leqslant T$,
\begin{equation}
(t-\tau)^{\vartheta-\eta}\|U_{A(u)}(t,\tau)-U_{A(v)}(t,\tau)\|_{\mathcal{L}(E_\eta,E_\vartheta)}\leqslant c\,\|u-v\|_{C([0,T],E_\beta)},
\end{equation} provided that 
$0\leqslant \vartheta \lt 1$ and 
$0 \lt \eta\leqslant 1$. Moreover, in view of (2.11), we have
\begin{align}
\|f(u(t))-f(v(t))\|_{\gamma}\leqslant c\, t^{-\mu q}\, d_{\mathcal{W}_T}(u,v) \,,\quad t\in (0,T].
\end{align} Letting 
$\theta\in \{\beta,\,\alpha,\,\xi\}$, we deduce from (2.9), (2.10), (2.20), and (2.21) that
\begin{align}
\|F(u)(t)-F(v)(t)\|_\theta &\leqslant \|U_{A(u)}(t,0)-U_{A(v)}(t,0)\|_{\mathcal{L}(E_\alpha,E_\theta)}\,\| u^0\|_{\alpha}\nonumber\\
&\quad+\int_0^t \|U_{A(u)}(t,\tau)-U_{A(v)}(t,\tau)\|_{\mathcal{L}(E_\gamma,E_\theta)} \,\|f(v(\tau))\|_\gamma\,\mathrm{d} \tau\nonumber\\
&\quad +\int_0^t \|U_{A(u)}(t,\tau)\|_{\mathcal{L}(E_\gamma,E_\theta)} \,\|f(u(\tau))-f(v(\tau))\|_\gamma\,\mathrm{d} \tau\nonumber\\
&\leqslant c\,\|u-v\|_{C([0,T],E_\beta)}\big(\|u^0\|_\alpha t^{\alpha-\theta}+t^{1+\gamma-\theta-\mu q}\big)\nonumber\\
&\quad + c\,d_{\mathcal{W}_T}(u,v)\, \max\big\{t^{1+\gamma_0-\theta-\mu q}, t^{1-\mu q}\}
\end{align} for all 
$t\in (0,T]$. Taking 
$\theta=\beta$ and 
$\theta=\xi$ in (2.22) implies that
\begin{align*}
&d_{\mathcal{W}_T}\big(F(u),F(v)\big)\\
&\leqslant c\, \big( T^{\alpha-\beta}+T^{1+\gamma_0-\beta-\mu q} + T^{1-\mu q}+T^{\mu+\alpha-\xi}
+T^{1+\gamma_0-\xi-\mu (q-1)}\big) \,d_{\mathcal{W}_T}(u,v).
\end{align*} Owing to (1.2e) and (2.7), we may make 
$T=T(S_\alpha)\in (0,1)$ smaller, if necessary, to obtain that
\begin{align*}
d_{\mathcal{W}_T}(F(u),F(v)) &\leqslant \frac{1}{2} \,d_{\mathcal{W}_T}(u,v)\,,\quad u,v\in \mathcal{W}_T.
\end{align*} This shows that 
$F:\mathcal{W}_T \to \mathcal{W}_T$ is a contraction for 
$T=T(S_\alpha)\in (0,1)$ small enough and thus has a unique fixed point 
$u=u(\cdot;u^0)\in \mathcal{W}_T$ according to Banach’s fixed point theorem.
Since the (Hölder) continuity property 
$u\in C^{\min\{\alpha-\theta,1-\mu q\}}\big([0,T], E_\theta\big)$ is established in (2.13) for 
${\theta\in[0,\alpha)}$, respectively in (2.13) and (2.17) for 
$\theta=\alpha$, it follows from (2.17) that u enjoys the regularity properties (2.3) for µ as chosen in (2.7) (and, in view of (2.1), also for larger values of µ). The arguments leading to (2.17) imply also that u is a strong solution to (1.1). That the regularity properties (2.17) hold for every 
$\mu \gt (\xi-\alpha)_+$ may be shown by arguing in a similar manner as below where the uniqueness claim is established.
Lipschitz continuity w.r.t. initial data and uniqueness. To establish the Lipschitz continuity of the solution with respect to the initial values, let 
${u^0, u^1\in Q_\alpha}$. We note for 
$\theta\in \{\beta,\,\alpha,\,\xi\}$ and 
$t\in (0,T]$ that
\begin{align*}
\|u(t;u^0)-u(t;u^1)\|_\theta&\leqslant\|U_{A(u(\cdot;u^1))}(t,0)\|_{\mathcal{L}(E_\alpha,E_\theta)}\|u^0-u^1\|_{\alpha} \\
&\quad +\|F(u(\cdot;u^0))(t)-F(u(\cdot;u^1))(t)\|_\theta.
\end{align*}In view of (2.9), we get
\begin{align*}
\|U_{A(u(\cdot;u^1))}(t,0)\|_{\mathcal{L}(E_\alpha,E_\theta)}\leqslant c\left\{
\begin{array}{lll}
1&,& \theta\in\{\beta,\,\alpha\},\\
t^{\alpha_0-\theta}&,&\theta=\xi,
\end{array}
\right.
\end{align*}while (2.22) yields
\begin{align*}
\| F(u(\cdot&;u^0))(t)-F(u(\cdot;u^1))(t)\|_\theta \\
&\leqslant c \|u(\cdot;u^0)-u(\cdot;u^1)\|_{C([0,T],E_\beta)} \big(t^{\alpha-\theta}+t^{1+\gamma-\theta-\mu q}\big) \\
&\quad + c\,d_{\mathcal{W}_T}(u(\cdot;u^0),u(\cdot;u^1))\, \max\big\{t^{1+\gamma_0-\theta-\mu q}, t^{1-\mu q}\}.
\end{align*} Hence, taking first 
$\theta=\beta$ and 
$\theta=\xi$ and making 
$T=T(S_\alpha)\in (0,1)$ smaller, if necessary, we derive
\begin{equation*}
d_{\mathcal{W}_T}\big(u(\cdot;u^0),u(\cdot;u^1)\big)\leqslant c\, \|u^0-u^1\|_{\alpha},
\end{equation*} and then, with 
$\theta=\alpha$, we deduce that indeed
\begin{equation*}
\|u(t;u^0)-u(t;u^1)\|_\alpha \leqslant c_0\, \|u^0-u^1\|_{\alpha}\,,\quad u^0, u^1\in Q_\alpha,
\end{equation*} for some constant 
$c_0=c_0(S_\alpha) \gt 0$.
Concerning the uniqueness claim, let 
$\tilde u$ be a solution to (1.1) with initial data 
${u^0\in Q_\alpha}$ with regularity stated in (2.4). In view of (2.1) we may assume that 
$q(\xi-\alpha)_+ \lt {\text{q}}\nu \lt \min\{1,1+\gamma-\alpha\}$. Let 
$u=u(\cdot;u^0)$. We choose
\begin{align*}
\widehat \rho\in\big(0,\min\{\rho,\, \vartheta\}\big)\qquad\text{and}\qquad \widehat \mu\in\Big(\max\{\mu,\, \nu\},\,\frac{1+\gamma-\alpha}{q}\Big)
\end{align*} and note that, if T is sufficiently small, then both functions u and 
$\tilde u$ belong to the complete metric space 
$\mathcal{W}_T$ (with 
$(\rho,\mu)$ replaced by 
$(\widehat \rho,\widehat \mu)$). The uniqueness claim follows now by arguing as in the first part of the proof where the existence of a solution was established.
Remark 2.2. An inspection of the proof of proposition 2.1 shows that the Hölder continuity in time and the assumption 
$\alpha \gt \beta$ are only needed to ensure (2.8b) while the assumption 
${\gamma \gt 0}$ and 
${\xi \lt 1}$ is only used when applying formula (2.20) to derive (2.22). That is, these assumptions are required to handle the quasilinear part and can thus be weakened for the semilinear problem (1.6); see the subsequent proof of proposition 3.1.
Proof of theorem 1.1
(i), (ii) Existence and uniqueness: Due to proposition 2.1, the Cauchy problem (1.1) admits for each 
$u^0\in O_\alpha=O_\beta\cap E_\alpha$ a unique local strong solution. By standard arguments it can be extended to a maximal strong solution 
$u(\cdot;u^0)$ on the maximal interval of existence 
$[0,t^+(u^0))$. The regularity properties of 
$u(\cdot;u^0)$ as stated in part (i) of theorem 1.1 and the uniqueness claim stated in part (ii) also follow from proposition 2.1.
(iii) Continuous dependence: Let 
$u^0\in O_\alpha$ and choose 
$t_0\in (0,t^+(u^0))$ arbitrarily. Fixing 
${t_*\in (t_0,t^+(u^0))}$, the set 
$S_\alpha:=u([0,t_*];u^0)\subset O_\alpha$ is compact. Thus, we infer from proposition 2.1 that there exist 
$\varepsilon=\varepsilon(S_\alpha) \gt 0$, 
$T=T(S_\alpha) \gt 0$, and 
$c_0=c_0(S_\alpha)\geqslant 1$ such that 
$T \lt t^+(u^1)$ for any
\begin{equation*}u^1\in Q_\alpha=\mathbb{B}_{E_\alpha}(S_\alpha,\varepsilon/(1+e_{\alpha,\beta})),\end{equation*}and
\begin{align}
\|u(t;u^1)-u(t; u^2)\|_{\alpha}\leqslant c_0 \|u^1- u^2\|_\alpha\,,\quad 0\leqslant t\leqslant T\,,\quad u^1, u^2\in Q_\alpha.
\end{align} Given 
$N\geqslant 1$ with 
$(N-1)T \lt t_*\leqslant NT$, we set 
$\varepsilon_0:=\varepsilon/((1+e_{\alpha,\beta})c_0^{N-1})$ and define the open neighbourhood 
$V_\alpha:=\mathbb{B}_{E_\alpha}(u^0,\varepsilon_0)$ of u 0 in Qα. We then claim that there is 
$k_0\geqslant1$ with
(1)
$t_* \lt t^+(u^1)$ for each $u^1\in V_\alpha$,(2)
$\|u(t;u^1)-u(t;u^0)\|_{\alpha} \leqslant k_0 \|u^1- u^0\|_\alpha$ for $0\leqslant t\leqslant t_*$ and $u^1\in V_\alpha$.
Indeed, let 
$u^1\in V_\alpha$. For 
$t_*\leqslant T$, this is exactly the above statement. If otherwise 
${T \lt t_*}$, then we have 
$u(T;u^0)\in S_\alpha$ and the estimate (see (2.23))
\begin{equation*}
\|u(t;u^1)-u(t; u^0)\|_{\alpha}\leqslant c_0 \|u^1- u^0\|_\alpha \lt \frac{\varepsilon}{1+e_{\alpha,\beta}}\,,\quad 0\leqslant t\leqslant T,
\end{equation*} entails 
$u(T;u^1)\in Q_\alpha$. Thus 
$T \lt t^+(u(T;u^i))$ for 
$i=0,1$, while the uniqueness of solutions to (1.1) ensures that 
$u(t;u(T;u^i))=u(t+T;u^i)$, 
$0\leqslant t\leqslant T$. Therefore, it follows from (2.23) that
\begin{equation*}
\|u(t+T;u^1)-u(t+T; u^0)\|_{\alpha}{\leqslant c_0\|u(T;u^1)-u(T; u^0)\|_{\alpha}}\leqslant c_0^2 \|u^1- u^0\|_\alpha
\end{equation*} for 
$0\leqslant t\leqslant T$. Now, if N = 2 we are done. Otherwise we proceed to derive (1) and (2) after finitely many iterations. In particular, property (1) implies that 
$(0,t_*)\times V_\alpha$ is a neighbourhood of 
$(t_0,u^0)$ in
\begin{equation*}
\mathcal{D}=\{(t,w)\,:\, 0\leqslant t \lt t^+(w)\,,\,w\in O_\alpha\}.
\end{equation*}This along with (2) implies the solution map defines a semiflow on Oα.
(iv) Global existence: Since the solution map defines a semiflow in Oα, it holds that 
$t^+(u^0)=\infty$ whenever the orbit 
$u([0,t^+(u^0));u^0)$ is relatively compact on Oα. This is part (iv) of theorem 1.1.
(v) Blow-up criterion: Let 
$u^0\in O_\alpha$ with 
$t^+(u^0) \lt \infty$. Assume now that the solution 
$u(\cdot;u^0):[0,t^+(u^0))\to E_\alpha$ is uniformly continuous but (1.4) was not true. Then, the limit 
$\lim_{t\nearrow t^+(u^0)}u(t;u^0)$ exists in 
$O_\alpha,$ so that 
$u([0,t^+(u^0));u^0)$ is relatively compact in Oα, which contradicts (iv) of theorem 1.1. This entails (a) from theorem 1.1 (v).
As for part (b) of theorem 1.1 (v), let E 1 be compactly embedded in E 0. Assume for contradiction that (1.5) was not true for some 
$\theta\in (\beta,1)$ that satisfies 
$(\xi-\theta)q \lt \min\{1,1+\gamma-\theta\}$. Without loss of generality we may further assume that 
${\theta \gt \alpha}$ (otherwise consider 
$\alpha_0\in (\beta,\theta)$ with 
$(\xi-\alpha_0)q \lt \min\{1,1+\gamma-\alpha_0\}$). Since then Eθ embeds compactly in Eα, we may find a sequence 
$t_n\nearrow t^+(u^0)$ such that 
$(u(t_n))_n$ converges in Eα and its limit lies in Oα. Using proposition 2.1 with Sα defined as the closure in Eα of the set 
$\{u(t_n)\,:\, n\in\mathbb{N}\}$, which is a compact subset of Oα, we may extend the maximal solution. This is a contradiction.
$\square$
3. Proof of theorem 1.2
The proof of theorem 1.2 is similar to the proof of theorem 1.1 with some modifications which are necessary to adapt to the weaker assumptions on the nonlinearity f. The analogue of proposition 2.1 reads as follows:
Proposition 3.1. Suppose (1.7) and let R > 0. Then, there exists 
${T:=T(R) \gt 0}$ such that, for each 
$u^0\in E_\alpha$ with 
$\|u^0\|_\alpha\leqslant R$, the problem (1.6) has a strong solution
\begin{equation}
\begin{aligned}
u=u(\cdot;u^0)\in &\ C^1\big((0,T],E_0\big)\cap C\big((0,T],E_1\big)\cap C \big([0,T],E_\alpha\big) \\
&\,\cap C^{\min\{\alpha-\theta,\,{ (1-\mu q)_+}\}}\big([0,T], E_\theta\big)\cap C_\mu\big((0,T],E_\xi\big)
\end{aligned}
\end{equation} for any 
$\theta\in [0,\alpha]$ and 
$\mu \gt \xi-\alpha$. Moreover, there is a constant 
$c_0(R) \gt 0$ such that
\begin{equation}
\| u(t;u^0)-u(t;u^1)\|_\alpha\leqslant c_0(R)\, \| u^0-u^1\|_\alpha\,,\qquad 0\leqslant t\leqslant T\,,\quad u^0, u^1\in \bar{\mathbb{B}}_{E_\alpha}(0,R).
\end{equation}Finally, if
\begin{equation*}\tilde u\in C^1\big((0,T],E_0\big)\cap C\big((0,T],E_1\big)\cap C \big([0,T],E_{\alpha}\big) \cap C_\nu\big((0,T],E_\xi\big)\end{equation*} with 
$\nu\geqslant 0$ and 
$q\nu \lt \min\{1,1+\gamma-\alpha\},$ is a solution to problem (1.6) which satisfies 
$\tilde u (0)=u^0 \in \bar{\mathbb{B}}_{E_\alpha}(0,R)$, then 
${\tilde u=u(\cdot;u^0)}$.
Proof. (i) Let 
$U_{A}(t,s)$, 
$ 0\leqslant s\leqslant t$, be the evolution operator associated with the map 
$A\in C^\rho(\mathbb{R}^+,\mathcal{H}(E_1,E_0))$ and recall from [Reference Amann8, II. lemma 5.1.3] that there exists a constant c > 0 such that
\begin{equation}
\|U_{A}(t,s)\|_{\mathcal{L}(E_\theta)} +(t-s)^{\theta-\vartheta_0}\|U_{A}(t,s)\|_{\mathcal{L}(E_\vartheta,E_\theta)} \leqslant c \,, \quad 0\leqslant s\leqslant t\leqslant 1,
\end{equation} for 
$0\leqslant \vartheta_0\leqslant \vartheta\leqslant \theta\leqslant 1$ with 
$\vartheta_0 \lt \vartheta$ if 
$0 \lt \vartheta \lt \theta \lt 1$. Recalling (1.7b) and (2.1), we may choose a positive constant µ such that
\begin{equation}
\xi-\alpha_0 \lt \mu \lt \min\left\{\frac{1}{q},\frac{1+\gamma_0-\alpha}{q}\right\}
\end{equation} for appropriate 
$\alpha_0\in (0,\alpha)$ if α > 0, respectively 
$\alpha_0:=0$ if α = 0 and, similarly, with 
$\gamma_0\in (0,\gamma)$ if γ > 0, respectively 
$\gamma_0:=0$ if γ = 0.
We then define for 
$T \in (0,1)$ the Banach space
\begin{equation*}
\mathcal{W}_T:=C([0,T],E_\alpha) \cap C_\mu((0,T],E_\xi).
\end{equation*} Given 
$u^0\in E_\alpha$ with 
$\|u^0\|_\alpha\leqslant R,$ we set
\begin{equation*}U_Au^0:=[t\mapsto U_A(t,0)u^0]\end{equation*} and deduce from [Reference Amann8, II. theorem 5.3.1], (3.3), and (3.4) that 
$U_Au^0\in \mathcal{W}_T$ satsifies 
$\|U_Au^0\|_{\mathcal{W}_T}\leqslant c(R)$ for some 
$c(R) \gt 0$. Consequently, if 
$u\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$, then
\begin{equation*}
\|u(t)\|_{\alpha}+t^{\mu}\|u(t)\|_\xi \leqslant c(R)\,,\quad t\in (0,T],
\end{equation*}and it follows from (1.7c) that
\begin{align}
\|f(u(t))\|_{\gamma}&\leqslant \|f(u(t))-f(0)\|_{\gamma} +\| f(0)\|_{\gamma}\leqslant c(R) t^{-\mu q}\,,\quad t\in (0,T].
\end{align} Also note for 
$u,v\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$ and 
$t\in (0,T]$ that
\begin{align}
\|f(u(t))-f(v(t))\|_{\gamma}\leqslant c(R) t^{-\mu q}
\big(\|u(t)-v(t)\|_{{\alpha}}+ t^{\mu } \|u(t)-v(t)\|_{\xi}\big).
\end{align} Define now for 
$ u\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$
\begin{equation}
F(u)(t):= U_{A}(t,0)u^0 +\int_0^t U_{A}(t,\tau) f(u(\tau))\,\mathrm{d} \tau\,,\quad t\in [0,T].
\end{equation} We claim that 
$F:\bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)\rightarrow \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$ defines a contraction if the constant 
$T=T(R)\in (0,1)$ is small enough.
(ii) Given 
$u\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$ we first note, as in the proof of proposition 2.1, that
\begin{equation*}u_\varepsilon:=u(\cdot+\varepsilon)\in C([0,T-\varepsilon],E_\xi)\,,\quad f(u_\varepsilon)\in C([0,T-\varepsilon],E_0),\end{equation*} for every 
$\varepsilon\in (0,T)$ so that [Reference Amann8, II. theorem 5.3.1] and (the analogue of) (2.16) yield
\begin{equation}
F(u)\in C\big((0,T],E_\theta\big)\,,\quad \theta\in (0,1).
\end{equation} Analogously to (2.18) we may use (3.3)-(3.5) and (3.8) (noticing that 
$(\gamma,\xi)\not=(0,1)$) to obtain 
$F(u)\in C_\mu((0,T],E_\xi)$ with
\begin{align}
\|F(u)-U_{A }u^0\|_{C_\mu((0,T],E_\xi)} &\leqslant \frac{1}{2},
\end{align} provided that 
$T=T(R)\in (0,1)$ is sufficiently small. Moreover, analogously to (2.13), we deduce that 
$F(u)\in C^{\min\{\alpha-\theta,1-\mu q\}}\big([0,T], E_\theta\big)$ for all 
$\theta\in[0,\alpha]$ and
\begin{equation}
\left\| F(u)- U_Au^0\right\|_{C([0,T],E_{\alpha})}\leqslant \frac{1}{2},
\end{equation} by making 
$T=T(R)\in (0,1)$ smaller, if necessary. Gathering (3.9) and (3.10) we obtain that the mapping 
$F:\bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big) \to \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$ is well-defined for 
$T=T(R)\in (0,1)$ small enough. Furthermore, using (3.3), (3.6), and the assumption 
$(\gamma,\xi)\not=(0,1)$, we may show analogously to (2.22) that
\begin{align}
\|F(u)(t)-F(v)(t)\|_\theta
&\leqslant c(R) \,d_{\mathcal{W}_T}(u,v)\, \max\big\{t^{1+\gamma_0-\theta-\mu q}, t^{1-\mu q}\}
\end{align} for 
$t\in (0,T]$, 
$\theta\in \{\alpha,\,\xi\}$, and 
$u,\,v\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$. Recalling (3.4), we may choose 
${T=T(R)\in (0,1)}$ sufficiently small to ensure that F is a contraction. Thus, F has a unique fixed point 
$u=u(\cdot;u^0)\in \bar{\mathbb{B}}_{\mathcal{W}_T}\big(U_Au^0,1\big)$.
(iii) In order to show that u is a strong solution to (1.6) with regularity (3.1), we handle the cases γ > 0 and γ = 0 separately.
If γ > 0, then 
$u\in C\big((0,T],E_1\big)\cap C^1\big((0,T],E_0\big)$ follows as in (2.17) by combining [Reference Amann8, II. theorem 1.2.2, II. remarks 2.1.2 (e)] and u is thus a strong solution.
If γ = 0, then 
${\xi \lt 1}$ by assumption. We consider again the map 
${u_\varepsilon:=u(\cdot+\varepsilon)}$ for 
${\varepsilon\in (0,T)}$ and note that 
$u_\varepsilon\in C([0,T-\varepsilon],E_\theta)$ for each 
$\theta\in (0,1)$, see (3.8). Taking 
$\theta\in (\xi,1)$, we then have 
$u_\varepsilon(0)\in E_\theta$ and 
$f(u_\varepsilon)\in C([0,T-\varepsilon],E_0)$. The latter properties, [Reference Amann8, II. theorem 5.3.1], and (the analogue of) (2.16) enable us to deduce that 
$u_\varepsilon\in C^{\theta-\xi}([0,T-\varepsilon],E_\xi)$. Along with the local Lipschsitz continuity property (1.7c) we get 
$f(u_\varepsilon)\in C^{\theta-\xi}([0,T-\varepsilon],E_0)$. Invoking now [Reference Amann8, II. theorem 1.2.1] we deduce
\begin{equation*}u_\varepsilon\in C\big((0,T-\varepsilon],E_1\big)\cap C^1\big((0,T-\varepsilon],E_0\big)\end{equation*} for each 
$\varepsilon\in (0,T)$, hence u is a strong solution to (1.6) enjoying the regularity properties (3.1) (for the constant µ fixed in Step 1). That (3.1) holds for every 
${\mu \gt \xi-\alpha}$ follows from the uniqueness property.
(iv) To establish the Lipschitz continuity with respect to the initial values, let 
$u^0, u^1\in \bar{\mathbb{B}}_{E_\alpha}(0,R)$ and note for 
$\theta\in \{\alpha,\,\xi\}$ and 
$t\in (0,T]$ that
\begin{align*}
\|u(t;u^0)-u(t;u^1)\|_\theta&\leqslant\|U_{A}(t,0)\|_{\mathcal{L}(E_\alpha,E_\theta)}\|u^0-u^1\|_{\alpha} \\
&\quad+\|F(u(\cdot;u^0))(t)-F(u(\cdot;u^1))(t)\|_\theta.
\end{align*} Hence, taking 
$\theta=\alpha$ and 
$\theta=\xi$ and using (3.3) and (3.11), we may make the constant 
$T=T(R)\in (0,1)$ smaller, if necessary, to deduce that
\begin{equation*}
\|u(t;u^0)-u(t;u^1)\|_\alpha \leqslant c_0(R)\, \|u^0-u^1\|_{\alpha}\,,\quad u^0, u^1\in \bar{\mathbb{B}}_{E_\alpha}(0,R)\,,\quad t\in [0,T],
\end{equation*} for some constant 
$c_0(R) \gt 0$.
(v) The uniqueness assertion is derived as in proposition 2.1.
The proof of theorem 1.2 now follows easily:
Proof of theorem 1.2
The existence and uniqueness of a maximal strong solution to the Cauchy problem (1.6) follows by standard arguments from proposition 3.1. Since 
$T=T(R) \gt 0$ in proposition 3.1 depends only on R, the blow-up criterion (1.8) readily follows when 
${t^+(u^0) \lt \infty}$. Moreover, if 
$A(t)=A\in \mathcal{H}(E_1,E_0)$ for 
$t\geqslant 0$, then (3.2) implies as in the proof of theorem 1.1 that the map 
${(t,u^0)\mapsto u(t;u^0)}$ is a semiflow on Eα. This then also ensures global existence for relatively compact orbits. 
$\square$
4. Basic preliminaries
In this section, we collect some general results which will be used in the applications presented in 
$\S$5 and 
$\S$6. By 
$W_{p}^{s}(\Omega)$ and 
$H_{p}^{s}(\Omega)$ for 
$s\in\mathbb{R}$ we denote the Sobolev-Slobodeckii spaces and the Bessel potential spaces, respectively [Reference Amann7, Reference Triebel35].
4.1. An auxiliary lemma
The following auxiliary lemma about Nemitskii operators is in the spirit of [Reference Amann3, proposition 15.4] (see also [Reference Walker36, lemma 2.7]) and may be useful in certain applications when verifying assumption (1.2d) (see e.g. 
$\S$6).
Lemma 4.1. Let 
$n,d\in \mathbb{N}^*$ and let Ω be an open subset of 
$\mathbb{R}^n$. Consider a function 
$g\in C^1(\mathbb{R}^d,\mathbb{R})$ with
\begin{equation}
\vert \nabla g(r)-\nabla g(s)\vert \leqslant c\big(1+\vert r\vert^{q-1}+\vert s\vert^{q-1}\big) \vert r-s\vert \,,\quad r,s\in\mathbb{R}^d,
\end{equation} for some constants 
$q\geqslant 1$ and c > 0. Let 
$p\in [1,\infty)$ and 
$\mu\in (0,1)$.
Then 
$g(w)\in W_{p}^{\mu}(\Omega)$ for every 
${w\in W_{p}^{\mu}(\Omega,\mathbb{R}^d)\cap L_\infty (\Omega,\mathbb{R}^d)}$. Moreover, there is a constant K > 0 such that for all 
$w_1,\, w_2\in W_{p}^{\mu}(\Omega,\mathbb{R}^d)\cap L_\infty (\Omega,\mathbb{R}^d)$ we have
\begin{equation*}
\begin{split}
&\|g(w_1)-g(w_2)\|_{W_{p}^\mu}\\
&\leqslant K \big(1+\| w_1\|_{\infty}^{q}+\| w_2\|_{\infty}^{q}\big) \| w_1-w_2\|_{W_{p}^\mu}\\
&\quad
+ K \big(1+\| w_1\|_{\infty}^{q-1}+\| w_2\|_{\infty}^{q-1}\big) \big(\| w_1\|_{W_{p}^\mu}+\| w_2\|_{W_{p}^\mu}\big) \| w_1-w_2\|_{\infty}.
\end{split}
\end{equation*}Proof. Note that (4.1) implies
\begin{equation}
\vert \nabla g(r)\vert \leqslant c_2\big(1+\vert r\vert^{q}\big) \,,\quad r\in\mathbb{R}^d.
\end{equation} Let 
$w_1,\, w_2\in W_{p}^{\mu}(\Omega,\mathbb{R}^d)\cap L_\infty (\Omega,\mathbb{R}^d)$. It then follows from the fundamental theorem of calculus, (4.1), and (4.2) that, for 
$x,\, y\in \Omega$,
\begin{equation*}
\begin{split}
&\big\vert \big(g(w_1(x))-g(w_2(x))\big)-
\big(g(w_1(y))-g(w_2(y))\big)\big\vert\\
&\leqslant \big|w_1(x)-w_2(x)-w_1(y)+w_2(y)\big|\int_0^1 \big|\nabla g\big(w_1(x)+\tau [w_1(x)-w_2(x)]\big)\big|\, \mathrm{d} \tau\\
&\quad + \big| w_1(y)-w_2(y)\big|\\
&\qquad\times\int_0^1 \left|\nabla g\big(w_1(x)+\tau
[w_1(x)-w_2(x)]\big)-\nabla g\big(w_1(y)+\tau
[w_1(y)-w_2(y)]\big)\right|\, \mathrm{d} \tau \\
&\leqslant c_3 \big(1+\|w_1\|_\infty^{q} +\|w_2\|_\infty^{q}\big) \,\big\vert w_1(x)-w_2(x)-w_1(y)+w_2(y)\big\vert \\
&\quad +c_3 \big( 1+\|w_1\|_\infty^{q-1}+\|w_2\|_\infty^{q-1} \big)\| w_1-w_2\|_\infty \, \big( \vert w_1(x)-w_1(y) \vert +\big\vert w_2(x)-w_2(y)\big\vert \big)
\!.
\end{split}
\end{equation*}The latter estimate together with (4.2) leads to
\begin{equation*}
\begin{split}
& \|g(w_1)-g(w_2)\|_{W_{p}^\mu}^p\\
&\leqslant\, \| g(w_1)-g(w_2)\|_{L_p}^p\\
&\quad + \int_{\Omega\times\Omega} \dfrac{\big\vert \big(g(w_1(x))-g(w_2(x))\big)-
\big(g(w_1(y))-g(w_2(y))\big)\big\vert^p}{\vert
x-y\vert^{n+\mu p}}\, \mathrm{d} (x,y)\\
&\leqslant c_4 \big(1+\| w_1\|_{\infty}^{q}+\| w_2\|_{\infty}^{q}\big)^p \| w_1-w_2\|_{W_p^\mu}^p\\
&\quad +c_4 \big( 1+\|w_1\|_\infty^{q-1}+\|w_2\|_\infty^{q-1} \big)^p\, \big( \| w_1\|_{W_p^\mu} +\| w_2\|_{W_p^\mu}\big)^p\,\| w_1-w_2\|_\infty^p
\end{split}
\end{equation*}as claimed.
4.2. Functional analytic setting for applications
We provide the underlying functional analytic setting for the applications in the next section. In order to include Dirichlet and Neumann boundary conditions on an open, bounded, smooth subset Ω of 
$\mathbb{R}^n$ with 
$n\in\mathbb{N}^*$, we fix 
$\delta\in\{0,1\}$ and define
\begin{equation*}
\mathcal{B}u:=u \ \text{on } \ \partial\Omega \ \text{if } \ \delta=0\,,\qquad \mathcal{B}u:=\partial_\nu u\ \text{on } \ \partial\Omega \ \text{if } \ \delta=1,
\end{equation*} that is, δ = 0 refers to Dirichlet boundary conditions and δ = 1 refers to Neumann boundary conditions. For a fixed 
$p\in (1,\infty)$ we introduce
\begin{equation*}F_0:=L_p(\Omega)\,,\qquad F_1:=W_{p,\mathcal B}^2(\Omega)=H_{p,\mathcal B}^2(\Omega)=\{v\in H_p^2(\Omega)\,:\,\mathcal Bv=0\text{on}\,\partial\Omega\},\end{equation*}and
\begin{equation*}
B_0:=\Delta_\mathcal{B}\in \mathcal{H}\big(W_{p,\mathcal{B}}^{2}(\Omega),L_p(\Omega)\big),
\end{equation*} cf. e.g. [Reference Amann7, §4], where 
$\Delta_\mathcal{B}$ denotes the Laplace operator with the boundary conditions introduced above. Let
\begin{equation*}
\big\{(F_\theta,B_\theta)\,:\, -1\leqslant \theta \lt \infty\big\}
\end{equation*} be the interpolation–extrapolation scale generated by 
$(F_0,B_0)$ and the complex interpolation functor 
$[\cdot,\cdot]_\theta$ (see [Reference Amann7, §6] and [Reference Amann8, §V.1]). That is,
\begin{equation}
B_\theta\in \mathcal{H}(F_{1+\theta},F_\theta)\,,\quad -1\leqslant \theta \lt \infty,
\end{equation} and, for 
$2\theta\neq -1-\delta+1/p$, we have (see [Reference Amann7, theorem 7.1; equation (7.5)]Footnote 1)
\begin{equation}
F_\theta\doteq H_{p,\mathcal{B}}^{2\theta}(\Omega):=\left\{\begin{array}{ll} \{v\in H_{p}^{2\theta}(\Omega) \,:\, \mathcal{B} v=0 \text{on}
\partial\Omega\}\,, &\delta+\frac{1}{p} \lt 2\theta \lt 2+\delta+\frac{1}{p} \,,\\[3pt]
H_{p}^{2\theta}(\Omega)\,, & -2+\frac{1}{p}+\delta \lt 2\theta \lt \delta +\frac{1}{p}.\end{array} \right.
\end{equation} Also note from [Reference Amann7, remarks 6.1 (d)] (since 
$\Delta_\mathcal{B}-1$ has bounded imaginary powers as follows e.g. from [Reference Amann8, III. examples 4.7.3 (d)]) the reiteration property
\begin{equation}
[F_\alpha,F_\beta]_\theta\doteq F_{(1-\theta)\alpha+\theta\beta}
\end{equation}and from [Reference Amann7, equations (5.2)-(5.6)] the embeddings
\begin{equation}
H_{p}^{s}(\Omega)\hookrightarrow W_{p}^{\tau}(\Omega)\hookrightarrow H_{p}^{t}(\Omega)\,,\quad t \lt \tau \lt s.
\end{equation} In the following, we use the letter D and N to indicate Dirichlet respectively Neumann boundary conditions (instead of 
$\mathcal{B}$).
Remark 4.2. The reason for working in the Bessel potential scale 
$H_{p,\mathcal{B}}^{s}(\Omega)$ is that it is stable under complex interpolation, see (4.4)-(4.5). However, using the almost reiteration property [Reference Amann8, I. remarks 2.11.2] (instead of (4.5)) and (4.6), one may work just as well in the Sobolev scale 
$W_{p,\mathcal{B}}^{s}(\Omega)$.
Finally, we recall a useful tool on pointwise multiplication:
Proposition 4.3. Let Ω be an open, bounded, smooth subset of 
$\mathbb{R}^{n}$. Let 
$m\geqslant 2$ be an integer and let 
${p,p_{j}\in [1,\infty)}$ and 
$s,s_{j}\in (0,\infty )$ for 
$1\leqslant j\leqslant m$ be real numbers satisfying 
$s \lt \min \{s_{j}\}$ along with 
$1/p\leqslant\sum_{j=1}^m1/p_j$ and
\begin{equation*}
s-\frac{n}{p} \lt \left\{
\begin{array}{ll}
\displaystyle{\sum\limits_{s_{j} \lt \frac{n}{p_{j}}}(s_{j}-\frac{n}{p_{j}})} &
\text{if} \quad \displaystyle{\min_{1\leqslant j\leqslant m}\left\{s_{j}-\frac{n}{p_{j}} \right\} \lt 0} \ , \\
\displaystyle{\min_{1\leqslant j \leqslant m}\left\{s_{j}-\frac{n}{p_{j}} \right\}} & \text{otherwise}.
\end{array}\right.
\end{equation*}Then pointwise multiplication
\begin{equation*}
\prod^{m}_{j=1}H_{p_{j}}^{s_{j}}(\Omega) \longrightarrow
H_{p}^{s}(\Omega )
\end{equation*}is continuous.
Proof. Proposition 4.3 is a consequence of the more general result stated in [Reference Amann6, theorem 4.1] (see also remarks 4.2 (d) therein) and the embeddings (4.6) (noticing that the Sobolev spaces 
$W_p^s(\Omega)$ coincide, for 
$s\in (0,\infty)\setminus\mathbb{N}$, with the Besov spaces 
$B_{p,p}^s(\Omega)$).
5. Applications of theorem 1.2 to chemotaxis systems
We illustrate the findings of our abstract result from theorem 1.2 for the semilinear case in the context of two chemotaxis systems, see (5.1) and (5.7). Exploiting the fact that we may choose 
${\xi \gt \alpha}$ in theorem 1.2, we prove local well-posedness for these chemotaxis systems in spaces of low regularity and obtain in this way quite general global existence criteria.
In the following, let Ω be an open, bounded, smooth subset of 
$\mathbb{R}^n$ with 
$n\in\mathbb{N}^*$.
5.1. Parabolic-parabolic equations
To begin with, we consider the cross-diffusion system
\begin{align}
\partial_t u&=\mathrm{div}\big(\nabla u-u\nabla v) +g(x,u,v)\,,&& t \gt 0\,,\quad x\in \Omega\,,
\end{align}
\begin{align}
\partial_t v&=\Delta v +u-v\,,&& t \gt 0\,,\quad x\in \Omega,
\end{align}where the nonlinearity g is assumed to be of polynomial form
\begin{align}
g(x,u,v)=\sum_{\ell=1}^M c_\ell(x) u^{m_\ell} v^{k_\ell}
\end{align} with 
$m_\ell,\, k_\ell,\, M\in \mathbb{N}$ and sufficiently smooth functions 
$c_\ell$ (in fact, 
$c_\ell\in H_p^r(\Omega)$ with 
${r \gt n/p}$). The evolution equations are subject to the initial conditions
\begin{align}
u(0,x)=u^0(x)\,, \quad v(0,x)=v^0(x)\,,\qquad x\in \Omega,
\end{align}and the boundary conditions
\begin{align}
\partial_\nu u= \partial_\nu v&= 0 \quad \text{on } \partial\Omega.
\end{align} Even though (5.1) has a natural quasilinear structure, we may derive its well-posedness from theorem 1.2 by formulating (5.1) as a semilinear evolution problem with different regularity and integrability assumptions for the variables u and v. The advantage of this approach compared to the quasilinear theory is discussed in remark 5.2 below. We also refer to [Reference Biler12, theorem 1] where the existence of local weak solutions to (5.1) for initial data 
$u_0\in L_p(\Omega)$ and 
$v_0\in H^1_p(\Omega)$ with p > n is established in the particular case g = 0 and n = 2. In fact, it is pointed out in [Reference Biler12, remarks] that one may weaken the restriction on u 0 and only assume that 
$u_0\in L_{p/2}(\Omega)$. As shown in the subsequent theorem 5.1, this is possible even in our setting of strong solutions and a function g containing at most quadratic nonlinearities in u, that is 
$\max\{\, m_1,\ldots,\, m_\ell\}\leqslant 2$. In particular, in the physically relevant dimensions 
$n\in\{1,\, 2,\, 3\}$, we prove that already a priori estimates for u in 
$L_2(\Omega)$ would guarantee that the strong solution is globally defined. In the case when 
${\max\{\, m_1,\ldots,\, m_\ell\}\geqslant 3}$, the nonlinearity g enforces more restrictive conditions on p, see remark 5.2 (a).
Theorem 5.1 Let 
$\max\{\, m_1,\ldots,\, m_\ell\}\leqslant 2$, choose 
$p\in (1,\infty) $ such that 
$p \gt n/2$, and let 
$q\in (n,\infty)$ satisfy
\begin{align*}
\frac{n}{p}-\frac{n}{q} \lt 1.
\end{align*} Then, the evolution problem (5.1) generates a semiflow on 
$ L_p(\Omega)\times H_{q}^{1}(\Omega)$. In particular, for each 
${(u^0,v^0)\in L_p(\Omega)\times H_{q}^{1}(\Omega)}$, the Cauchy problem (5.1) possesses a maximal strong solution
\begin{equation*}
(u,v)\in C \big([0,t^+),L_p(\Omega)\times H_{q}^{1}(\Omega)\big)
\end{equation*} with regularity properties stated in (5.5) below. Moreover, if (u, v) is not globally defined, that is, if 
$t^+ \lt \infty$, then
\begin{align*}
\limsup_{t\nearrow t^+}\|u(t)\|_{L_p}=\infty.
\end{align*}Before providing the proof of theorem 5.1 we note:
Remarks 5.2.
(a) Theorem 5.1 remains true if 
$m:=\max\{m_1,\ldots,\, m_\ell\}\geqslant 3$ for the particular choice 
$p=q \gt (m-1)n$. The proof of this result is similar to that of theorem 5.1 and therefore omitted.
(b) In order to allow for quite general initial data, we shall consider the equation (5.1a) in a Bessel potential space of negative order. Nevertheless, a subsequent bootstrapping argument shows that 
${(u,v)\in C^\infty((0,t^+)\times\bar\Omega, \mathbb{R}^2)}$ provided that 
${c_\ell\in C^\infty(\bar\Omega)}$ for 
$1\leqslant \ell\leqslant M$.
(c) We emphasize that it is not at all clear whether the choice
\begin{equation*}(u^0,v^0)\in L_p(\Omega) \times H^{1}_q(\Omega)\end{equation*} for the initial data in theorem 5.1 is possible when using the quasilinear parabolic theory in [Reference Amann7] instead of theorem 1.2, even if g = 0 and 
$p=q \gt n$. Indeed, considering the evolution problem (5.1) in the ambient space 
$H_{p,N}^{2\sigma}(\Omega)\times H_{p,N}^{2\tau}(\Omega)$, the term 
${\mathrm{div}\big(\nabla u-u\nabla v)}$ in (5.1a) can be handled in several ways, either quasilinear
\begin{align*}
&A_1(w)z:=\Delta z_1- \mathrm{div}\big(z_1\nabla v)\,,\qquad A_2(w)z:=\Delta z_1- \mathrm{div}\big(u\nabla z_2),
\end{align*} for 
$w=(u,v)$ and 
$z=(z_1,z_2)\in \mathrm{dom}(A_i(w)),$ or semilinear
\begin{align*}
& A_3z:=\Delta z_1\ \text{with }\ f(w):=\mathrm{div}\big(u\nabla v)
\end{align*} for 
$z=(z_1,z_2)\in \mathrm{dom}(A_3)$. One then minimally requires that 
$2\sigma,\, 2\tau \gt -1+1/p$ (to identify the extrapolation scale). In order to achieve 
$A_1(w)z\in H_{p,N}^{2\sigma}(\Omega)$, one needs 
$z_1\nabla v\in H_{p}^{2\sigma+1}(\Omega)$, hence 
${v\in H_{p}^{2\sigma+2}(\Omega)}$ with 
${2\sigma+2 \gt 1,}$ so that a general 
$v^0\in H_p^1(\Omega)$ is not possible when using [Reference Amann7]. Similarly, 
$A_2(w)z\in H_{p,N}^{2\sigma}(\Omega)$ requires 
${u\nabla z_2\in H_{p}^{2\sigma+1}(\Omega)}$ and hence 
$u\in H_{p}^{2\sigma+1}(\Omega)$ with 
$2\sigma+1 \gt 0$ so that it seems impossible to take 
$u^0\in L_p(\Omega)$. Finally, in order to have 
$f(w)\in H_{p,N}^{2\sigma}(\Omega)$, one needs 
$u\nabla v\in H_{p}^{2\sigma+1}(\Omega)$ with 
${2\sigma+1 \gt 0}$, and hence neither 
${u^0\in L_p(\Omega)}$ nor 
${v^0\in H_p^1(\Omega)}$ seems possible.
We now establish the proof of theorem 5.1.
Proof of theorem 5.1
Let ɛ be such that
\begin{align*}
0 \lt 2\varepsilon \lt \min\Big\{1-\frac{1}{p},\, 1-\frac{n}{q},\, 1 -\frac{n}{p}+\frac{n}{q}\Big\}
\end{align*}and define
\begin{align}
&E_0:= H_{p,N}^{-2\varepsilon}(\Omega)\times H_{q,N}^{1-2\varepsilon}(\Omega)\,, &E_1:= H_{p,N}^{2-2\varepsilon}(\Omega)\times H_{q,N}^{3-2\varepsilon}(\Omega),
\end{align}so that
\begin{equation*}
E_\theta=H_{p,N}^{-2\varepsilon+2\theta}(\Omega)\times H_{q,N}^{1-2\varepsilon+2\theta}(\Omega)\,,\quad 2\theta\in [0,2]\setminus\{1+1/p+2\varepsilon\,,\, 1/q+2\varepsilon\}.
\end{equation*}Set
\begin{align*}
0 \lt \gamma:=\frac{\varepsilon}{3} \lt \alpha:=\varepsilon \lt \xi=\frac{1+\varepsilon}{2} \lt 1.
\end{align*}It follows that
\begin{equation}
2(\xi-\alpha) \lt \min \,\{1,\,1+\gamma-\alpha\}
\end{equation} and, recalling (4.4)-(4.5), we have 
$E_\alpha= L_p(\Omega)\times H_{q}^{1}(\Omega)$ and
\begin{align*}
E_\xi= H_{p,N}^{1- \varepsilon}(\Omega)\times H_{q,N}^{2- \varepsilon}(\Omega)\hookrightarrow E_\alpha\hookrightarrow E_\gamma= H_{p,N}^{- 4\varepsilon/3}(\Omega)\times H_{q,N}^{1- 4\varepsilon/3}(\Omega).
\end{align*} Since 
$H_{p,N}^{2-2\varepsilon}(\Omega)\hookrightarrow H_{q,N}^{1-2\varepsilon}(\Omega),$ we obtain from [Reference Amann8, I. theorem 1.6.1] and (4.3)-(4.4) that
\begin{equation*}
A:=\begin{pmatrix}
\Delta&0\\
1&\Delta-1
\end{pmatrix}\in \mathcal{H}(E_1,E_0),
\end{equation*} where the symbol Δ in the diagonal entries of A stands for (different) extrapolated versions of 
$\Delta_\mathcal{B}$ with 
${\mathcal{B}=N}$, see (4.3), that depend on ɛ. Defining 
$f:= f_1+f_2 $ with
\begin{align*}
f_1(w):=\big( -\mathrm{div}\big(u\nabla v),0\big) \qquad\text{and}\qquad f_2(w):=\Big( \sum_{\ell=1}^M c_\ell(x) u^{m_\ell} v^{k_\ell},0\Big)
\end{align*} for 
$w:=(u,v)$, we may thus recast (5.1) as a semilinear parabolic Cauchy problem
\begin{equation*}
w'=A w+f(w)\,,\quad t \gt 0\,,\qquad w(0)=w^0:=(u^0,v^0).
\end{equation*} We next show that 
$f:E_\xi\to E_\gamma$ is well-defined and that, given R > 0, there is a constant 
$c(R) \gt 0$ such that
\begin{equation}
\begin{aligned}
&\|f(w)-f(\bar w)\|_{E_\gamma}\\
&\leqslant c(R)\big[1+\|w \|_{E_\xi}+\|\bar w\|_{E_\xi}\big]\big[\big(1+\|w \|_{E_\xi}+\|\bar w\|_{E_\xi}\big) \|w -\bar w\|_{{E_\alpha}}+\|w-\bar w\|_{E_\xi}\big]
\end{aligned}
\end{equation} for all 
$w,\, \bar w\in E_\xi$ with 
$\|w\|_{E_\alpha},\, \|\bar w\|_{E_\alpha}\leqslant R.$ To this end we estimate, for each 
$w\in E_\xi$ with 
${\|w\|_{E_\alpha}\leqslant R,}$
\begin{align*}
\|f_1(w)\|_{H^{-4\varepsilon/3}_{p,N}} \leqslant c\|u\nabla v\|_{H^{1-4\varepsilon/3}_{p,N}}\leqslant c\|u\|_{H^{1-\varepsilon}_{p,N}}\|v\|_{H^{2-\varepsilon}_{q,N}}\leqslant c\|w\|_{E_\xi}^2,
\end{align*}where the continuity of the multiplication
\begin{align*}
H_{p,N}^{1- \varepsilon}(\Omega)\bullet H_{q,N}^{1- \varepsilon}(\Omega)\longrightarrow H_{p,N}^{1- 4\varepsilon/3}(\Omega)
\end{align*} is used in the second step of the estimate (note that 
$1-\varepsilon \gt n/q)$, see proposition 4.3. Moreover, since 
$H_{q,N}^{2- \varepsilon}(\Omega)$ is an algebra with respect to the pointwise multiplication, 
$\max\{\, m_1,\ldots,\, m_\ell\}\leqslant 2$, and since the multiplication
\begin{align*}
H_{p,N}^{1- \varepsilon}(\Omega)\bullet H_{p,N}^{1- \varepsilon}(\Omega)\longrightarrow L_p(\Omega)
\end{align*} is continuous according to proposition 4.3, we have (assuming that 
$c_\ell\in H_p^r(\Omega)$ with 
$r \gt n/p$)
\begin{align*}
\|f_2(w)\|_{H^{-4\varepsilon/3}_{p,N}} \leqslant c \|f_2(w)\|_{L_p} \leqslant c(R)(1+\|u\|_{L_p}+\|u\|_{L_p}^2) \leqslant c(R)(1+\|w\|_{E_\xi}^2).
\end{align*} This proves that 
$f:E_\xi\to E_\gamma$ is well-defined. Arguing as above, it is straightforward to show now that the local Lipschitz continuity property (5.4) is satisfied. We are thus in position to apply theorem 1.2 to deduce that the evolution problem (5.1) generates a semiflow in 
$E_\alpha=L_p(\Omega)\times H_{q}^{1}(\Omega)$. In particular, for each 
$w^0\in E_\alpha$, there exists a maximal strong solution
\begin{equation}
w=(u,v)\in C^1\big((0,t^+(w^0)),E_0\big)\cap C\big((0,t^+(w^0)),E_1\big)\cap C \big([0,t^+(w^0)),E_\alpha\big)
\end{equation}to (5.1), with E 0 and E 1 defined in (5.2).
Let 
$w=(u,v) \in C ([0,t^+),E_\alpha)$ be a maximal solution to (5.1) with finite maximal existence time 
$t^+=t^+(w^0) \lt \infty$. We then have
\begin{equation}
\limsup_{t\nearrow t^+}\|w(t)\|_{E_{\alpha}}=\limsup_{t\nearrow t^+}\|(u(t),v(t))\|_{L_p \times H_{q}^{1}}=\infty.
\end{equation} Assume that u is bounded in 
$L_p(\Omega).$ We may also assume 
$w^0\in E_1,$ hence 
${v^0\in H_{q,N}^2(\Omega)\hookrightarrow H_{p,N}^{2-2\varepsilon}(\Omega)}.$ It then follows from (5.1b) that v is bounded in 
$H^{2-2\varepsilon}_{p,N}(\Omega),$ hence also in 
$H^{1}_{q,N}(\Omega) $ due to the embedding 
${H^{2-2\varepsilon}_{p,N}(\Omega)\hookrightarrow H^{1}_{q,N}(\Omega)}$. Consequently, (5.6) is equivalent to
\begin{equation*}
\limsup_{t\nearrow t^+}\|u(t)\|_{L_p}=\infty.
\end{equation*}This proves the claim.
5.2. A degenerate chemotaxis system
We consider the quasilinear evolution problem
\begin{align}
\partial_t u&=\mathrm{div}(\nabla u-u\nabla w)\,, && t \gt 0\,,\quad x\in \Omega\,,
\end{align}
\begin{align}
\partial_t v&=u-v\,,\,\ \ \ \ \ && \qquad\quad t \gt 0\,,\quad x\in \Omega\,,
\end{align}
\begin{align}
\partial_t w&=\Delta w+v-w\,,\,\,\,\,\,\,\,\,\,\,\, && t \gt 0\,,\quad x\in \Omega\,,
\end{align}subject to the initial conditions
\begin{align}
u(0,x)=u^0(x)\,,\quad v(0,x)=v^0(x)\,,\quad w(0,x)=w^0(x)\,,\qquad x\in \Omega,
\end{align}and the boundary conditions
\begin{align}
\partial_\nu u&= \partial_\nu w=0 \quad \text{on } \partial\Omega.
\end{align} This particular chemotaxis system is investigated in [Reference Laurençot21] (see also [Reference Amann5] for a general strategy to handle this type of problems). Although equations (5.7a) and (5.7c) are coupled through highest order terms, we proceed as in the previous 
$\S$5.1 and consider different regularities and integrability properties for the variables 
$u,\, v,$ and w to reformulate (5.7) as a semilinear parabolic evolution problem. An application of theorem 1.2 enables us to impose rather low regularities on the initial data and to derive sharp global existence criteria.
Theorem 5.3 Let 
$q\in (\max\{1,\, n-1\},\infty)$ and 
$1 \lt p\leqslant q$ with
\begin{equation}
\frac{n}{p}-\frac{n}{q} \lt 1.
\end{equation} Let 
$s, \tau\in\mathbb{R}$ satisfy
\begin{align*}
s\in \left(\max\left\{ \,-1+\frac{1}{p}\,,\,-1+\frac{n}{q}\right\},\frac{1}{q}\right)
\end{align*}and
\begin{align*}
\tau\in\left( \max\left\{\frac{n}{p}\,,\,\frac{n+1}{p}-\frac{n}{q}\right\}\,,\, s+2\right)\setminus\left\{1+\frac{1}{p}\right\}.
\end{align*} Then (5.7) generates a semiflow on 
$H_{p,N}^s(\Omega)\times H_{p}^\tau(\Omega)\times H_{q,N}^{s+1}(\Omega)$. In particular, for each initial value 
$(u^0,v^0, w^0)\in H_{p,N}^s(\Omega)\times H_{p}^\tau(\Omega)\times H_{q,N}^{s+1}(\Omega)$, the Cauchy problem (5.7) possesses a maximal strong solution
\begin{align*}
(u,v,w)\in C \big([0,t^+),{H_{p,N}^s(\Omega)\times H_{p}^\tau(\Omega)\times H_{q,N}^{s+1}(\Omega)}\big)
\end{align*} with regularity properties stated in (5.12). Moreover, if 
$(u,v, w)$ is not globally defined, then
\begin{equation}
\limsup_{t\nearrow t^+}\|u(t)\|_{H_{p}^s}=\infty.
\end{equation}Before establishing the proof of theorem 5.3, we note:
Remark 5.4. If q > n and 
$p\in (1,q]$ satisfy the condition (5.8), then one may choose s = 0 (and an arbitrary 
${\tau\in \big(\max\{n/p,(n+1)/p-n/q\}, 2\big)} \setminus\{1+1/p\}$ to obtain a semiflow on 
${L_p(\Omega)\times H_{p}^\tau(\Omega)\times H_{q}^{1}(\Omega)}$. In this case, solutions are global provided
\begin{align*}
\sup_{t\in [0,t^+)\cap [0,T]}\|u(t)\|_{L_p} \lt \infty\quad \text{for each}\ T \gt 0.
\end{align*} If 
$q=2p \gt n$, one may choose s = 0 and 
$\tau\in \big(\max\{n/p,(n+2)/(2p)\}, 2\big)$. Hence, a priori estimates for u in 
$L_2(\Omega)$ ensure that the strong solution is globally defined in the physically relevant dimensions 
$n\in\{1,\, 2,\, 3\}$. For such estimates see [Reference Laurençot21].
We now establish theorem 5.3.
Proof of theorem 5.3
The assumptions on s and τ along with (5.8) imply that we can choose a number a such that
\begin{equation*}
\max\big\{\tau-2\,,\, -1+n/q\,,\,-1+1/p\big\} \lt a \lt \min\big\{\tau-1-n/p+n/q\,,\,s\big\},
\end{equation*} that is, 
$a\in \big(\max\{-1+n/q,-1+1/p\},s\big)$ and
\begin{equation}
a+1+\frac{n}{p}-\frac{n}{q} \lt \tau \lt a+2.
\end{equation}Set
\begin{align}
E_\theta:= H_{p,N}^{a+2\theta}(\Omega)\times H_{p}^{\tau}(\Omega) \times H_{q,N}^{a+1+2\theta}(\Omega)\,,\quad
2\theta\in [0,2]\setminus\left\{1/q-a \,,\, 1+1/p-a \right\}.
\end{align} We note that the middle component is independent of θ and that all spaces belong to the scale of (4.4). We then have 
$E_\theta=[E_0,E_1]_\theta$. Set
\begin{equation*}
2\alpha:=s-a\in (0,1)\setminus\left\{1/q-a \,,\, 1+1/p-a \right\}\,,\quad \gamma:=0,
\end{equation*}and choose
\begin{equation*}
2\xi\in(1,1+\alpha)\setminus \left\{1/q-a,\, 1+1/p-a\right\}.
\end{equation*} Note that 
$0=\gamma \lt \alpha \lt \xi \lt 1$. Since 
$H_{p,N}^{a+2}(\Omega)\hookrightarrow H_{p}^{\tau}(\Omega)\hookrightarrow H_{q,N}^{a+1}(\Omega)$ due to (5.10), we obtain from [Reference Amann8, I. theorem 1.3.1] and (4.3)-(4.4) that
\begin{equation*}
A:=\begin{pmatrix}
\Delta&0&0\\
0&-1&0\\
0&0&\Delta-1
\end{pmatrix}+\begin{pmatrix}
0&0&0\\
1&0&0\\
0&1&0
\end{pmatrix}\in \mathcal{H}(E_1,E_0),
\end{equation*} where Δ stands again for (different) extrapolated versions of 
$\Delta_\mathcal{B}$ with 
$\mathcal{B}=N$, see (4.3). Setting
\begin{equation*}
f(z):=\big(-\mathrm{div}(u\nabla w),0,0\big)\,,\quad z=(u,v,w),
\end{equation*}we may thus recast (5.7) as the semilinear autonomous parabolic Cauchy problem
\begin{equation*}
z'=Az+f(z)\,,\quad t \gt 0\,,\qquad z(0)=z^0:=(u^0,v^0,w^0),
\end{equation*} in E 0. Since 
$a+2\xi \gt a+1 \gt n/q$, we derive continuity of the pointwise multiplication
\begin{align*}
H_{p}^{a+2\xi}(\Omega)\bullet H_{q}^{a+2\xi}(\Omega)\hookrightarrow H_{p}^{a+1}(\Omega),
\end{align*}and therefore
\begin{align*}
\|\mathrm{div}\big(u\nabla w\big)\|_{H_{p}^{a}} \leqslant c\|u\nabla w\|_{H_{p}^{a+1}} \leqslant c\|u\|_{H_{p}^{a+2\xi}}\|w\|_{H_{q}^{a+1+2\xi}}\,,\quad z=(u,v,w)\in E_\xi.
\end{align*}We thus have
\begin{equation*}
\begin{split}
\|f(z_1)-f(z_2)\|_{E_0}
\leqslant c\big(\|z_1\|_{E_\xi} +\|z_2\|_{E_\xi} \big)\|z_1-z_2\|_{E_\xi}\,,\quad z_1,\, z_2\in E_\xi,
\end{split}
\end{equation*} hence 
$f:E_\xi\to E_0$ satisfies (1.7c) (with q = 2 therein). Since 
$2\xi \lt 1+\alpha$, also assumption (1.7b) is satisfied and we infer from theorem 1.2 that (5.7) generates a semiflow on
\begin{equation*}
E_\alpha= H_{p,N}^{s}(\Omega)\times H_{p}^{\tau}(\Omega)\times H_{q,N}^{s+1}(\Omega).
\end{equation*} In particular, for each 
$z^0=(u^0,v^0,w^0)\in H_{p,N}^{s}(\Omega)\times H_{p }^{\tau}(\Omega)\times H_{q,N}^{s+1}(\Omega)$ there is a unique maximal strong solution
\begin{equation}
z=(u,v,w)\in C^1\big([0,t^+),E_0\big)\cap C\big((0,t^+),E_1\big)\cap C \big([0,t^+),E_\alpha\big),
\end{equation} to (5.7), see (5.11) for the definition of E 0 and E 1. Moreover, if 
$t^+ \lt \infty$, then
\begin{equation}
\limsup_{t\nearrow t^+}\|(u(t),v(t),w(t))\|_{H_{p}^s\times H_{p}^\tau\times H_{q}^{s+1}}=\infty.
\end{equation} Finally, consider a maximal solution 
$z=(u,v,w)$ on the maximal existence interval 
${J:=[0,t^+)}$ such that 
$t^+ \lt \infty$ and
\begin{equation*}
\|u(t)\|_{H_{p}^s}\leqslant c_0 \lt \infty\,,\quad t\in J.
\end{equation*} We may assume without loss of generality that 
$u^0\in H_{p,N}^{a+2}(\Omega)$ and 
$w^0\in H_{p,N}^{s+2}(\Omega)$ (as 
$s-a \lt 1$). Observing that 
$\tau \gt s$, we infer from the bound on u and (5.7b) that
\begin{equation*}
\|v(t)\|_{H_{p}^s}\leqslant c_1 \lt \infty\,,\quad t\in J.
\end{equation*} In turn, since s > a and 
$w^0\in H_{p,N}^{s+2}(\Omega),$ we have 
$w\in BUC^{\vartheta}\big(J,H_{p,N}^{s+2-2\rho}(\Omega)\big)$ for some 
${\rho \gt \vartheta \gt 0}$ with
\begin{align*}
2\rho \lt \min\Big\{s-a,\, 1-\frac{n}{p}+\frac{n}{q}\Big\}
\end{align*} from the latter estimate, equation (5.7c), and [Reference Amann8, II. theorem 5.3.1]. In view of the embedding 
$H_{p,N}^{s+2-2\rho}(\Omega)\hookrightarrow H_{q,N}^{s+1}(\Omega)$ we get
\begin{equation*}
\|w(t)\|_{H_{q}^{s+1}}\leqslant c_2 \lt \infty\,,\quad t\in J.
\end{equation*} Moroever, since 
$a+2 \gt \tau \gt n/p$, the pointwise multiplication
\begin{align*}
H_{p,N}^{\tau}(\Omega) \bullet H_{p,N}^{s-2\rho+1}(\Omega)\hookrightarrow H_{p,N}^{a+1}(\Omega)
\end{align*} is continuous and 
$ H_{p,N}^{a+2}(\Omega)\hookrightarrow H_{p,N}^{\tau}(\Omega)$. Setting
\begin{align*}
B(t)y:=\Delta_N y-\mathrm{div}\big(y\nabla w(t)\big)\,,\quad y\in H_{p,N}^{a+2}(\Omega)\,,\quad t\in J,
\end{align*}we may now deduce from [Reference Amann8, I. theorem 1.3.1, I.Corollary 1.3.2] that
\begin{align*}
B\in BUC^{\vartheta}\big(J,\mathcal{L}(H_{p,N}^{a+2}(\Omega),H_{p,N}^{a}(\Omega))\big)
\end{align*} satisfies 
$B(t)\in \mathcal{H}(H_{p,N}^{a+2}(\Omega),H_{p,N}^{a}(\Omega);\kappa,\omega),$ 
$t\in J$, for some 
$\kappa\geqslant 1$ and ω > 0. Noticing that
\begin{equation*}
u'(t)= B(t)u(t)\,,\quad t\in J\,,\qquad u(0)=u^0,
\end{equation*}according to (5.7a), we conclude from [Reference Amann8, II. theorem 5.4.1] that
\begin{equation*}
\|u(t)\|_{H_{p,N}^{a+2}}\leqslant c_3\,,\quad t\in J.
\end{equation*} Invoking again (5.7b) and recalling that 
$a+2 \gt \tau$, we finally obtain that
\begin{equation*}
\|(u(t),v(t),w(t))\|_{H_{p}^s\times H_{p}^\tau\times H_{q}^{s+1}}\leqslant c_4\,,\quad t\in J,
\end{equation*} for some constant 
$c_4 \lt \infty$, in contradiction to (5.13). This ensures the global existence criterion (5.9).
6. Application to chemotaxis systems with density-suppressed motility
We consider a model for autonomous periodic stripe pattern formation (see [Reference Jiang, Laurençot and Zhang19] and the literature therein)
\begin{align}
\partial_t u&=\Delta(u\chi(v))+ug(m)\,,&& t \gt 0\,,\quad x\in \Omega\,,
\end{align}
\begin{align}
\partial_t v&=\Delta v +u-v\,,\,\ \ \ \,\,\,\,\, && \quad\, t \gt 0\,,\quad x\in \Omega,
\end{align}
\begin{align}
\partial_t m&=\Delta m-ug(m)\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, && t \gt 0\,,\quad x\in \Omega,\,\,
\end{align}subject to the initial conditions
\begin{align}
u(0,x)=u^0(x)\,,\quad v(0,x)=v^0(x)\,,\quad m(0,x)=m^0(x)\,,\qquad x\in \Omega,
\end{align}and the boundary conditions
\begin{align}
\partial_\nu (u\chi(v))= \partial_\nu v&= \partial_\nu m=0 \quad \text{on } \partial\Omega.
\end{align} The following theorem 6.1 is a consequence of theorem 1.1 and establishes the existence and uniqueness of strong solutions only assuming 
$u^0\in L_p(\Omega)$ with 
$p \gt 2n$ (in fact, as shown in the proof, even less is required), which does not seem to be derivable from [Reference Amann7] directly. In the proof of theorem 6.1, we take full advantage of the fact that we may choose 
${\xi \gt \alpha}$ (in this context we actually have 
$\xi-\alpha \gt 1/2$). The global existence criterion (6.3) thus simplifies the one obtained in [Reference Jiang, Laurençot and Zhang19] for this system being based on a priori 
$L_\infty$-estimates for u.
Theorem 6.1 Let 
$p\in (2n,\infty)$, 
$g\in C^{2-}(\mathbb{R})$, and 
$\chi\in C^{3-}(\mathbb{R})$ with 
$\chi(r)\geqslant \chi_0 \gt 0$ for 
$r\in\mathbb{R}$. Let further 
$\varepsilon\in(0,1/p)$ and κ > 0 satisfy
\begin{equation*}
\frac{2n}{p} \lt 2\kappa \lt 1-5\varepsilon,
\end{equation*}and set
\begin{equation*}
\bar\sigma:=-1+\frac{n}{p}+5\varepsilon\,,\qquad \bar\kappa:=2\kappa+4\varepsilon\,,\qquad \bar\tau:=\frac{n}{p}+4\varepsilon.
\end{equation*} Then (6.1) generates a semiflow on 
$H_{p,N}^{\bar\sigma}(\Omega)\times H_{p,N}^{\bar\kappa}(\Omega)\times H_{p,N}^{\bar\tau}(\Omega)$. In particular, for each initial value 
$(u^0,v^0, m^0)\in H_{p,N}^{\bar\sigma}(\Omega)\times H_{p,N}^{\bar\kappa}(\Omega)\times H_{p,N}^{\bar\tau}(\Omega)$, the Cauchy problem (6.1) possesses a maximal strong solution
\begin{align*}
(u,v,m)\in C \big([0,t^+),H_{p,N}^{\bar\sigma}(\Omega)\times H_{p,N}^{\bar\kappa}(\Omega)\times H_{p,N}^{\bar\tau}(\Omega)\big)
\end{align*} with regularity properties stated in (6.14). Moreover, if 
$(u,v, m)$ is a maximal solution such that 
${t^+ \lt \infty}$, then
\begin{equation}
\limsup_{t\nearrow t^+}\left\|(u(t),m(t))\right\|_{L_p \times H_{p}^{1}}=\infty.
\end{equation} In fact, if 
$g\geqslant 0$ and 
$(u^0,v^0,m^0)\in L_p(\Omega)\times H^1_{p,N}(\Omega)\times H_{p}^{1}(\Omega)$ are non-negative, then 
$t^+ \lt \infty$ implies
\begin{equation}
\limsup_{t\nearrow t^+}\left\|u(t) \right\|_{L_p}=\infty.
\end{equation}Before establishing the proof of theorem 6.1 we note:
Remark 6.2. The parameters are chosen such that 
$L_p(\Omega)\times H_{p}^1(\Omega)\times H_{p}^{1}(\Omega)$ is contained in the space 
$H_{p,N}^{\bar\sigma}(\Omega)\times H_{p,N}^{\bar\kappa}(\Omega)\times H_{p,N}^{\bar\tau}(\Omega)$ of initial data.
We now present the proof of theorem 6.1.
Proof of theorem 6.1
For 
$w=(u,v,m)$ and 
$w^0=(u^0,v^0,m^0)$ we may recast (6.1) as a quasilinear Cauchy problem
\begin{equation}
w'=A(w)w+f(w)\,,\quad t \gt 0\,,\qquad w(0)=w^0,
\end{equation}by formally setting
\begin{equation}
A(w):=\big[(z_1,z_2,z_3)\mapsto \big(\mathrm{div}\big(\chi(v)\nabla z_1\big),(\Delta-1)z_2+z_1,\Delta z_3\big]
\end{equation}and
\begin{equation}
f(w):=\big(\mathrm{div}\big(u\chi'(v)\nabla v\big)+u g(m),0,-u g(m)\big)
\end{equation}on suitable spaces which we introduce now. To this end, we set
\begin{equation*}
2\sigma:=-1+\frac{n}{p}+\varepsilon\,,\qquad \alpha:=2\varepsilon\,,\qquad 2\tau:=\frac{n}{p},
\end{equation*}and define
\begin{align}
E_\theta:=H_{p,N}^{2\sigma+2\theta}(\Omega)\times H_{p,N}^{2\kappa+2\theta}(\Omega)\times H_{p,N}^{2\tau+2\theta}(\Omega)\,,\quad \theta\in[0,1],
\end{align} and note from (4.4)-(4.5), since 
$2\sigma\in (-1+1/p,0)$ and 
$2\kappa+2,\, 2\tau+2\in(2,3)$, that
\begin{align*}
&E_\theta=[E_0,E_1]_\theta=H_{p,N}^{2\sigma+2\theta}(\Omega)\times H_{p,N}^{2\kappa+2\theta}(\Omega)\times H_{p,N}^{2\tau+2\theta}(\Omega)\,,\quad \theta\in [0,1]\setminus\Sigma,
\end{align*}where
\begin{align*}
\Sigma:=\Big\{\frac{1}{2}\Big(1+\frac{1}{p}-2\sigma\Big),\,\frac{1}{2}\Big(1+\frac{1}{p}-2\kappa\Big),\, \frac{1}{2}\Big(1+\frac{1}{p}-2\tau\Big)\Big\}.
\end{align*}We further set
\begin{equation*}
\gamma:=\varepsilon\,,\qquad \beta:=\frac{3\varepsilon}{2} \,,\qquad \xi:=\frac{1}{2}+\frac{9\varepsilon}{8},
\end{equation*} and note that 
$0 \lt \gamma \lt \beta \lt \alpha \lt \xi \lt 1$ and 
$\gamma,\, \beta,\,\alpha,\, \xi\not\in\Sigma $. We choose a constant 
$\kappa'$ such that 
$2\kappa \gt 2\kappa' \gt 2n/p$ and note that, since
\begin{equation*}
2\kappa'+2\beta-\frac{n}{p} \gt \frac{n}{p}+ 3\varepsilon=:\rho\in(0,1),
\end{equation*} we have 
${H_p^{2\kappa'+2\beta}(\Omega)\hookrightarrow C^{\rho}(\bar\Omega)}$. Moreover, lemma 4.1 and (4.6) imply
\begin{equation*}
[v\mapsto \chi(v)]\in C^{1-}\big(H_p^{2\kappa+2\beta}(\Omega),H_p^{2\kappa'+2\beta}(\Omega)\big).
\end{equation*} Noticing that 
$H_{p,N}^{2\sigma+1}(\Omega)$ is an algebra with respect to pointwise multiplication and 
${2\kappa'+2\beta \gt 2\sigma+1}$, we now infer from [Reference Amann7, theorem 8.5]Footnote 2 that for
\begin{equation*}
A_1(v)z_1:= \mathrm{div}\big(\chi(v)\nabla z_1\big)
\end{equation*}we have
\begin{equation}
A_1\in C^{1-}\big(H_p^{2\kappa+2\beta}(\Omega),\mathcal{H}\big(H_{p,N}^{2\sigma+2}(\Omega),H_{p,N}^{2\sigma}(\Omega)\big)\big).
\end{equation}Now, we obtain from (6.8), (4.3)-(4.4) together with
\begin{equation*}
H_{p,N}^{2\sigma+2}(\Omega)\hookrightarrow H_{p,N}^{1}(\Omega)\hookrightarrow H_{p,N}^{2\kappa}(\Omega),
\end{equation*}and a standard perturbation argument for the second component that, with A defined in (6.5),
\begin{equation}
\big[w\mapsto A(w)\big]\in C^{1-}\big(E_\beta,\mathcal{H}(E_1,E_0)\big).
\end{equation}As for the nonlinear part f, we first note from proposition 4.3 that the pointwise multiplication
\begin{equation}
H_p^{2\sigma+2\xi}(\Omega)\bullet H_p^{2\kappa'+2\beta}(\Omega)\bullet H_p^{2\kappa+2\xi-1}(\Omega)\longrightarrow H_p^{2\sigma+2\gamma+1}(\Omega)
\end{equation} is continuous since 
$2\xi \gt 2\gamma+1$, 
$ 2\sigma+2\gamma+1=n/p+3\varepsilon \gt n/p$, and
\begin{align*} 2\kappa'+2\beta=2\kappa'+3\varepsilon \gt \frac{2n}{p}+3\varepsilon \gt \frac{n}{p}+3\varepsilon ,\qquad 2\kappa+2\xi-1 \gt \frac{2n}{p}+2\varepsilon \gt \frac{n}{p}+3\varepsilon.
\end{align*} Consider in the following 
$w=(u,v,m)\in E_\xi$ with 
$\|w\|_{E_\beta}\leqslant R$. Since
\begin{equation*}
[h\mapsto \chi'(h)]\in C^{1-}\big(H_p^{2\kappa+2\beta}(\Omega),H_p^{2\kappa'+2\beta}(\Omega)\big)
\end{equation*}is bounded on bounded sets according to lemma 4.1 and (4.6), we deduce from (6.10) that
\begin{equation}
\left\|\mathrm{div}\big(u\chi'(v)\nabla v\big)\right\|_{H_p^{2\sigma+2\gamma}}\leqslant c(R)\|u\|_{H_p^{2\sigma+2\xi}}\,\|v\|_{H_p^{2\kappa+2\xi}}.
\end{equation}Noticing that also the pointwise multiplication
\begin{equation*}
H_p^{2\sigma+2\xi}(\Omega)\bullet H_p^{2\tau+\gamma+ \beta}(\Omega) \longrightarrow H_p^{2\tau+2\gamma}(\Omega)\hookrightarrow H_p^{2\sigma+2\gamma}(\Omega)
\end{equation*} is continuous, since 
$2\tau \gt 2\sigma$, 
$2\tau+\gamma+ \beta \gt 2\tau+2\gamma \gt n/p$, and
\begin{equation*}
2\sigma+2\xi \gt \frac{n}{p}+2\varepsilon=2\tau+2\gamma,
\end{equation*}and the mapping
\begin{equation*}
[m\mapsto g(m)]\in C^{1-}\big(H_p^{2\tau+2\beta}(\Omega),H_p^{2\tau+\gamma+ \beta}(\Omega)\big)
\end{equation*}is bounded on bounded sets (see again lemma 4.1 and (4.6)), we derive that
\begin{equation}
\|u g(m)\|_{H_p^{2\sigma+2\gamma}}\leqslant c \|u g(m)\|_{H_p^{2\tau+2\gamma}}\leqslant c(R)\|u\|_{H_p^{2\sigma+2\xi}}.
\end{equation}It then follows from (6.11)-(6.12) and the definition of f in (6.6) that
\begin{equation}
\begin{aligned}
&\|f(w)-f(\bar w)\|_{E_\gamma}\\
&\leqslant c(R)\big[1+\|w\|_{E_\xi}+\|\bar w\|_{E_\xi}\big]\big[ \big(\|w\|_{E_\xi}+\|\bar w\|_{E_\xi}\big) \|w-\bar w\|_{E_\beta}+\|w-\bar w\|_{E_\xi}\big]
\end{aligned}
\end{equation} for 
$w, \bar w\in E_\xi$ with 
$\|w\|_{E_\beta}, \|\bar w\|_{E_\beta}\leqslant R$.
Setting 
$q=2,$ it follows that the assumptions of theorem 1.1 are fulfilled in the context of the quasilinear evolution problem (6.4). Consequently, the solution map associated with (6.4) defines a semiflow on
\begin{align*}
E_\alpha=H_{p,N}^{2\sigma+2\alpha}(\Omega)\times H_{p,N}^{2\kappa+2\alpha}(\Omega)\times H_{p,N}^{2\tau+2\alpha}(\Omega)
= H_{p,N}^{\bar\sigma}(\Omega)\times H_{p,N}^{\bar\kappa}(\Omega)\times H_{p,N}^{\bar\tau}(\Omega).
\end{align*} In particular, for each 
$w^0\in E_\alpha $, there exists a unique maximal strong solution
\begin{equation}
w=(u,v,m)\in C^1\big((0,t^+(w^0)),E_0\big)\cap C\big((0,t^+(w^0)),E_1\big)\cap C \big([0,t^+(w^0)),E_\alpha\big)
\end{equation}to (6.1), see (6.7) for the definition of E 0 and E 1. Noticing that
\begin{equation*}
L_p(\Omega) \times H_{p}^{1}(\Omega)\times H_{p}^{1}(\Omega)\hookrightarrow E_\alpha
\end{equation*} since 
$\bar\sigma \lt 0$ and 
$\bar\kappa, \bar\tau \lt 1$, we thus have
\begin{equation}
\lim_{t\nearrow t^+}\left\|(u(t),v(t),m(t))\right\|_{L_p \times H_{p}^{1}\times H_{p}^{1}}=\infty
\end{equation} for any maximal strong solution 
$w=(u,v,m)$ to (6.1) on 
$J=[0,t^+)$ with 
$t^+ \lt \infty$. We may assume that 
$w^0\in H_{p,N}^{1}(\Omega)\times H_{p,N}^{2 }(\Omega)\times H_{p,N}^{2 }(\Omega)$. Then, if 
$\|u(t)\|_{L_p}\leqslant c_0$ for 
$t\in J$, we have 
$\|v(t)\|_{H_p^1}\leqslant c_1$ for 
$t\in J$ according to (6.1c), so that (6.15) reduces to (6.2).
Finally, assume that 
$g\geqslant 0$ and let 
$(u^0,v^0,m^0)\in L_p(\Omega)\times H^1_{p,N}(\Omega)\times H_{p}^{1}(\Omega)$ satisfy 
$u^0,v^0,m^0\geqslant 0$ a.e. in Ω. The comparison principle (together with a density argument and the semiflow property) yields 
${u(t),v(t),m(t) \geqslant 0}$ a.e. in Ω for all 
$t\in J$. We may assume, via a bootstrapping argument, that the initial values belong to 
$H^3_{p,N}(\Omega)$. Using again the comparison principle together with (6.1c) we get 
${\|m(t)\|_\infty\leqslant \|m^0\|_\infty}$ for all 
$t\in J$. In particular, we obtain that 
$\|g(m(t))\|_\infty\leqslant c_2$ for 
$t\in J$. Assume now that 
$t^+ \lt \infty$ and 
${\|u(t)\|_{L_p}\leqslant c_0}$ for 
$t\in J$. Then 
$\|u(t)g(m(t))\|_{L_p}\leqslant c_3$ for 
$t\in J$ and hence 
$\|m(t)\|_{H_p^1}\leqslant c_4$ for 
${t\in J}$ due to (6.1c), in contradiction to (6.2). Consequently, we obtain (6.3) if 
$t^+ \lt \infty$.
Acknowledgements
We thank the referee for carefully reading the paper and for valuable suggestions.
