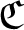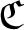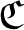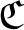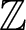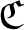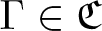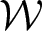1. Introduction
Let ![]() $\mathcal{W}$ be the Razak–Jacelon algebra studied in [Reference Jacelon15] (see also [Reference Razak33]). By classification results in [Reference Castillejos and Evington2] and [Reference Elliott, Gong, Lin and Niu6] (see also [Reference Nawata30]),
$\mathcal{W}$ be the Razak–Jacelon algebra studied in [Reference Jacelon15] (see also [Reference Razak33]). By classification results in [Reference Castillejos and Evington2] and [Reference Elliott, Gong, Lin and Niu6] (see also [Reference Nawata30]), ![]() $\mathcal{W}$ is the unique simple separable nuclear monotracial
$\mathcal{W}$ is the unique simple separable nuclear monotracial ![]() $\mathcal{Z}$-stable C
$\mathcal{Z}$-stable C![]() $^*$-algebra that is KK-equivalent to
$^*$-algebra that is KK-equivalent to ![]() $\{0\}$. Also,
$\{0\}$. Also, ![]() $\mathcal{W}$ is regarded as a stably finite analog of the Cuntz algebra
$\mathcal{W}$ is regarded as a stably finite analog of the Cuntz algebra ![]() $\mathcal{O}_2$. More generally, we can consider that
$\mathcal{O}_2$. More generally, we can consider that ![]() $\mathcal{W}$ is a non-unital analog of strongly self-absorbing C
$\mathcal{W}$ is a non-unital analog of strongly self-absorbing C![]() $^*$-algebras. (Note that every strongly self-absorbing C
$^*$-algebras. (Note that every strongly self-absorbing C![]() $^*$-algebra is unital by definition.) In this article, we study group actions on
$^*$-algebra is unital by definition.) In this article, we study group actions on ![]() $\mathcal{W}$ and show an analogous result of Szabó’s result in [Reference Szabó40] for group actions on strongly self-absorbing C
$\mathcal{W}$ and show an analogous result of Szabó’s result in [Reference Szabó40] for group actions on strongly self-absorbing C![]() $^*$-algebras (see also [Reference Izumi and Matui12–Reference Izumi and Matui14, Reference Matui22–Reference Matui and Sato24, Reference Matui and Sato26, Reference Szabó37, Reference Szabó39] for pioneering works). We refer the reader to [Reference Izumi11] for the importance and some difficulties of studying group actions on C
$^*$-algebras (see also [Reference Izumi and Matui12–Reference Izumi and Matui14, Reference Matui22–Reference Matui and Sato24, Reference Matui and Sato26, Reference Szabó37, Reference Szabó39] for pioneering works). We refer the reader to [Reference Izumi11] for the importance and some difficulties of studying group actions on C![]() $^*$-algebras. Gabe and Szabó classified outer actions of countable discrete amenable groups on Kirchberg algebras up to cocycle conjugacy in [Reference Gabe and Szabó7]. In their classification,
$^*$-algebras. Gabe and Szabó classified outer actions of countable discrete amenable groups on Kirchberg algebras up to cocycle conjugacy in [Reference Gabe and Szabó7]. In their classification, ![]() $\mathcal{O}_2$ and
$\mathcal{O}_2$ and ![]() $\mathcal{O}_{\infty}$ play central roles. Hence it is natural to expect that
$\mathcal{O}_{\infty}$ play central roles. Hence it is natural to expect that ![]() $\mathcal{W}$ plays a central role in the classification theory of group actions on ‘classifiable’ stably finite (at least stably projectionless) C
$\mathcal{W}$ plays a central role in the classification theory of group actions on ‘classifiable’ stably finite (at least stably projectionless) C![]() $^*$-algebras.
$^*$-algebras.
Let ![]() $\mathfrak{C}$ be the smallest class of countable discrete groups with the following properties: (i)
$\mathfrak{C}$ be the smallest class of countable discrete groups with the following properties: (i) ![]() $\mathfrak{C}$ contains the trivial group, (ii)
$\mathfrak{C}$ contains the trivial group, (ii) ![]() $\mathfrak{C}$ is closed under isomorphisms, countable increasing unions and extensions by
$\mathfrak{C}$ is closed under isomorphisms, countable increasing unions and extensions by ![]() $\mathbb{Z}$. (We say that Γ is an extension by
$\mathbb{Z}$. (We say that Γ is an extension by ![]() $\mathbb{Z}$ if there exists an exact sequence
$\mathbb{Z}$ if there exists an exact sequence ![]() $1\to H \to \Gamma \to \mathbb{Z}\to 1$.) Note that
$1\to H \to \Gamma \to \mathbb{Z}\to 1$.) Note that ![]() $\mathfrak{C}$ is the same class as in [Reference Szabó40, definition B]. It is easy to see that
$\mathfrak{C}$ is the same class as in [Reference Szabó40, definition B]. It is easy to see that ![]() $\mathfrak{C}$ contains all countable discrete torsion-free abelian groups and poly-
$\mathfrak{C}$ contains all countable discrete torsion-free abelian groups and poly-![]() $\mathbb{Z}$ groups, and
$\mathbb{Z}$ groups, and ![]() $\mathfrak{C}$ is a subclass of the class of countable discrete torsion-free elementary amenable groups. Szabó showed that if
$\mathfrak{C}$ is a subclass of the class of countable discrete torsion-free elementary amenable groups. Szabó showed that if ![]() $\Gamma\in \mathfrak{C}$ and
$\Gamma\in \mathfrak{C}$ and ![]() $\mathcal{D}$ is a strongly self-absorbing C
$\mathcal{D}$ is a strongly self-absorbing C![]() $^*$-algebra, then there exists a unique strongly outer action of Γ on
$^*$-algebra, then there exists a unique strongly outer action of Γ on ![]() $\mathcal{D}$ up to cocycle conjugacy [Reference Szabó40, corollary 3.4]. In this article, we show an analogous result of this result. Indeed, the main theorem in this article is the following theorem.
$\mathcal{D}$ up to cocycle conjugacy [Reference Szabó40, corollary 3.4]. In this article, we show an analogous result of this result. Indeed, the main theorem in this article is the following theorem.
Theorem A (theorem 4.3)
Let Γ be a countable discrete group in ![]() $\mathfrak{C}$, and let α be a strongly outer action of Γ on
$\mathfrak{C}$, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. Then α is cocycle conjugate to
$\mathcal{W}$. Then α is cocycle conjugate to ![]() $\mu^{\Gamma}\otimes \mathrm{id}_{\mathcal{W}}$ on
$\mu^{\Gamma}\otimes \mathrm{id}_{\mathcal{W}}$ on ![]() $M_{2^{\infty}}\otimes\mathcal{W}$ where
$M_{2^{\infty}}\otimes\mathcal{W}$ where ![]() $\mu^{\Gamma}$ is the Bernoulli shift action of Γ on
$\mu^{\Gamma}$ is the Bernoulli shift action of Γ on  $\bigotimes_{g\in \Gamma}M_{2^{\infty}}\cong M_{2^{\infty}}$.
$\bigotimes_{g\in \Gamma}M_{2^{\infty}}\cong M_{2^{\infty}}$.
We say that an action α on ![]() $\mathcal{W}$ is
$\mathcal{W}$ is ![]() $\mathcal{W}$-absorbing if there exists a simple separable nuclear monotracial C
$\mathcal{W}$-absorbing if there exists a simple separable nuclear monotracial C![]() $^*$-algebra A and an action β on A such that α is cocycle conjugate to
$^*$-algebra A and an action β on A such that α is cocycle conjugate to ![]() $\beta\otimes\mathrm{id}_{\mathcal{W}}$ on
$\beta\otimes\mathrm{id}_{\mathcal{W}}$ on ![]() $A\otimes\mathcal{W}$. The proof of the main theorem above is based on a characterization in [Reference Nawata31] of strongly outer
$A\otimes\mathcal{W}$. The proof of the main theorem above is based on a characterization in [Reference Nawata31] of strongly outer ![]() $\mathcal{W}$-absorbing actions of countable discrete amenable groups. Actually, we use the following theorem that is a slight variant of [Reference Nawata31, theorem 8.1]. Note that
$\mathcal{W}$-absorbing actions of countable discrete amenable groups. Actually, we use the following theorem that is a slight variant of [Reference Nawata31, theorem 8.1]. Note that ![]() $F(\mathcal{W})$ is Kirchberg’s central sequence C
$F(\mathcal{W})$ is Kirchberg’s central sequence C![]() $^*$-algebra of
$^*$-algebra of ![]() $\mathcal{W}$. Furthermore,
$\mathcal{W}$. Furthermore, ![]() $F(\mathcal{W})^{\alpha}$ is the fixed point algebra for the action on
$F(\mathcal{W})^{\alpha}$ is the fixed point algebra for the action on ![]() $F(\mathcal{W})$ induced by an action α on
$F(\mathcal{W})$ induced by an action α on ![]() $\mathcal{W}$. Let
$\mathcal{W}$. Let ![]() $\mathrm{Sp}(x)$ denote the spectrum of x.
$\mathrm{Sp}(x)$ denote the spectrum of x.
Theorem B (theorem 2.4)
Let α be a strongly outer action of a countable discrete amenable group Γ on ![]() $\mathcal{W}$. Then α is cocycle conjugate to
$\mathcal{W}$. Then α is cocycle conjugate to ![]() $\mu^{\Gamma}\otimes\mathrm{id}_{\mathcal{W}}$ on
$\mu^{\Gamma}\otimes\mathrm{id}_{\mathcal{W}}$ on ![]() $M_{2^{\infty}}\otimes \mathcal{W}$ if and only if α satisfies the following properties:
$M_{2^{\infty}}\otimes \mathcal{W}$ if and only if α satisfies the following properties:
(i) there exists a unital
 $*$-homomorphism from
$*$-homomorphism from  $M_{2}(\mathbb{C})$ to
$M_{2}(\mathbb{C})$ to  $F(\mathcal{W})^{\alpha}$,
$F(\mathcal{W})^{\alpha}$,(ii) if x and y are normal elements in
 $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that  $\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and
$\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and  $0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any
$0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any  $f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$, then x and y are unitary equivalent in
$f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$, then x and y are unitary equivalent in  $F(\mathcal{W})^{\alpha}$,
$F(\mathcal{W})^{\alpha}$,(iii) there exists an injective
 $*$-homomorphism from
$*$-homomorphism from  $\mathcal{W}\rtimes_{\alpha}\Gamma$ to
$\mathcal{W}\rtimes_{\alpha}\Gamma$ to  $\mathcal{W}$.
$\mathcal{W}$.
We use a first cohomology vanishing type theorem (corollary 3.4) for showing that if ![]() $\Gamma\in \mathfrak{C}$ and α is a strongly outer action of Γ on
$\Gamma\in \mathfrak{C}$ and α is a strongly outer action of Γ on ![]() $\mathcal{W}$, then
$\mathcal{W}$, then ![]() $F(\mathcal{W})^{\alpha}$ satisfies the properties (i) and (ii) in the theorem above. Kishimoto’s techniques for Rohlin type theorems in [Reference Kishimoto19] and [Reference Kishimoto20], Herman-Ocneanu’s argument in [Reference Herman and Ocneanu9], and homotopy type arguments in [Reference Nawata28] enable us to show this first cohomology vanishing type theorem. Also, note that our arguments for
$F(\mathcal{W})^{\alpha}$ satisfies the properties (i) and (ii) in the theorem above. Kishimoto’s techniques for Rohlin type theorems in [Reference Kishimoto19] and [Reference Kishimoto20], Herman-Ocneanu’s argument in [Reference Herman and Ocneanu9], and homotopy type arguments in [Reference Nawata28] enable us to show this first cohomology vanishing type theorem. Also, note that our arguments for ![]() $F(\mathcal{W})^{\alpha}$ are based on results that are shown by techniques around (equivariant) property (SI) in [Reference Matui and Sato25–Reference Matui and Sato27, Reference Sato34–Reference Sato36, Reference Szabó42].
$F(\mathcal{W})^{\alpha}$ are based on results that are shown by techniques around (equivariant) property (SI) in [Reference Matui and Sato25–Reference Matui and Sato27, Reference Sato34–Reference Sato36, Reference Szabó42].
2. Preliminaries
2.1. Notations and basic definitions
Let α and β be actions of a countable discrete group Γ on C![]() $^*$-algebras A and B, respectively. We say that α is conjugate to β if there exists a isomorphism φ from A onto B such that
$^*$-algebras A and B, respectively. We say that α is conjugate to β if there exists a isomorphism φ from A onto B such that ![]() $\varphi\circ \alpha_g=\beta_g\circ \varphi$ for any
$\varphi\circ \alpha_g=\beta_g\circ \varphi$ for any ![]() $g\in \Gamma$. Note that α induces an action on the multiplier algebra M(A) of A. We denote it by the same symbol α. An α-cocycle on A is a map from Γ to the unitary group of M(A) such that
$g\in \Gamma$. Note that α induces an action on the multiplier algebra M(A) of A. We denote it by the same symbol α. An α-cocycle on A is a map from Γ to the unitary group of M(A) such that ![]() $u_{gh}=u_{g}\alpha_g(u_h)$ for any
$u_{gh}=u_{g}\alpha_g(u_h)$ for any ![]() $g,h\in \Gamma$. We say that α is cocycle conjugate to β if there exist an isomorphism φ from A onto B and a β-cocycle u such that
$g,h\in \Gamma$. We say that α is cocycle conjugate to β if there exist an isomorphism φ from A onto B and a β-cocycle u such that ![]() $\varphi\circ \alpha_g=\mathrm{Ad}(u_g)\circ \beta_g \circ \varphi$ for any
$\varphi\circ \alpha_g=\mathrm{Ad}(u_g)\circ \beta_g \circ \varphi$ for any ![]() $g\in\Gamma$. An action α of Γ on A is said to be outer if αg is not an inner automorphism of A for any
$g\in\Gamma$. An action α of Γ on A is said to be outer if αg is not an inner automorphism of A for any ![]() $g\in \Gamma\setminus \{\iota\}$ where ι is the identity of Γ. We denote by A α and
$g\in \Gamma\setminus \{\iota\}$ where ι is the identity of Γ. We denote by A α and ![]() $A\rtimes_{\alpha}\Gamma$ the fixed point algebra and the reduced crossed product C
$A\rtimes_{\alpha}\Gamma$ the fixed point algebra and the reduced crossed product C![]() $^*$-algebra, respectively.
$^*$-algebra, respectively.
Assume that A has a unique tracial state τA. Let ![]() $(\pi_{\tau_{A}}, H_{\tau_{A}})$ be the Gelfand–Naimark–Segal representation of τA. Then
$(\pi_{\tau_{A}}, H_{\tau_{A}})$ be the Gelfand–Naimark–Segal representation of τA. Then ![]() $\pi_{\tau_{A}}(A)^{\prime\prime}$ is a finite factor and α induces an action
$\pi_{\tau_{A}}(A)^{\prime\prime}$ is a finite factor and α induces an action ![]() $\tilde{\alpha}$ on
$\tilde{\alpha}$ on ![]() $\pi_{\tau_{A}}(A)^{\prime\prime}$. We say that α is strongly outer if
$\pi_{\tau_{A}}(A)^{\prime\prime}$. We say that α is strongly outer if ![]() $\tilde{\alpha}$ is an outer action on
$\tilde{\alpha}$ is an outer action on ![]() $\pi_{\tau_{A}}(A)^{\prime\prime}$. (We refer the reader to [Reference Gardella, Hirshberg and Vaccaro8] and [Reference Matui and Sato26] for the definition of strongly outerness for more general settings.)
$\pi_{\tau_{A}}(A)^{\prime\prime}$. (We refer the reader to [Reference Gardella, Hirshberg and Vaccaro8] and [Reference Matui and Sato26] for the definition of strongly outerness for more general settings.)
We denote by ![]() $\mathcal{R}_0$ and
$\mathcal{R}_0$ and ![]() $M_{2^{\infty}}$ the injective II1 factor and the canonical anticommutation relations (CAR) algebra, respectively.
$M_{2^{\infty}}$ the injective II1 factor and the canonical anticommutation relations (CAR) algebra, respectively.
2.2. Fixed point algebras of Kirchberg’s central sequence C $^*$-algebras
$^*$-algebras
Let ω be a free ultrafilter on ![]() $\mathbb{N}$, and put
$\mathbb{N}$, and put
 \begin{equation*}
A^{\omega}:= \ell^{\infty}(\mathbb{N}, A)/\{\{x_n\}_{n\in\mathbb{N}}\in \ell^{\infty}(\mathbb{N}, A)\; |
\; \lim_{n\to\omega} \|x_n \|=0 \}.
\end{equation*}
\begin{equation*}
A^{\omega}:= \ell^{\infty}(\mathbb{N}, A)/\{\{x_n\}_{n\in\mathbb{N}}\in \ell^{\infty}(\mathbb{N}, A)\; |
\; \lim_{n\to\omega} \|x_n \|=0 \}.
\end{equation*} We denote by ![]() $(x_n)_n$ a representative of an element in A ω. We identify A with the C
$(x_n)_n$ a representative of an element in A ω. We identify A with the C![]() $^*$-subalgebra of A ω consisting of equivalence classes of constant sequences. Set
$^*$-subalgebra of A ω consisting of equivalence classes of constant sequences. Set
 \begin{equation*}\mathrm{Ann}(A,A^\omega):=\{(x_n)_n\in A^\omega\cap A^{\prime}\;\vert\;\lim_{n\rightarrow\omega}\Arrowvert x_na\Arrowvert=0\,\text{for any }a\in A\}.\end{equation*}
\begin{equation*}\mathrm{Ann}(A,A^\omega):=\{(x_n)_n\in A^\omega\cap A^{\prime}\;\vert\;\lim_{n\rightarrow\omega}\Arrowvert x_na\Arrowvert=0\,\text{for any }a\in A\}.\end{equation*} Then ![]() $\mathrm{Ann}(A, A^{\omega})$ is an closed ideal of
$\mathrm{Ann}(A, A^{\omega})$ is an closed ideal of ![]() $A^{\omega}\cap A^{\prime}$, and define
$A^{\omega}\cap A^{\prime}$, and define
See [Reference Kirchberg17] for basic properties of F(A). For a finite von Neumann algebra M, put
 \begin{equation*}
M^{\omega}:=\ell^{\infty}(\mathbb{N}, M)/\{\{x_n\}_{n\in\mathbb{N}}\in \ell^{\infty}(\mathbb{N}, M)
\; |\; \lim_{n\to\omega}\| x_n\|_2=0\}
\end{equation*}
\begin{equation*}
M^{\omega}:=\ell^{\infty}(\mathbb{N}, M)/\{\{x_n\}_{n\in\mathbb{N}}\in \ell^{\infty}(\mathbb{N}, M)
\; |\; \lim_{n\to\omega}\| x_n\|_2=0\}
\end{equation*}and
Note that we identify M with the subalgebra of M ω consisting of equivalence classes of constant sequences and Mω is the von Neumann algebraic central sequence algebra (or the asymptotic centralizer) of M.
For a tracial state τA on A, define a map ![]() $\tau_{A, \omega}$ from F(A) to
$\tau_{A, \omega}$ from F(A) to ![]() $\mathbb{C}$ by
$\mathbb{C}$ by ![]() $\tau_{A, \omega}([(x_n)_n])=\lim_{n\to\omega}\tau_A(x_n)$ for any
$\tau_{A, \omega}([(x_n)_n])=\lim_{n\to\omega}\tau_A(x_n)$ for any ![]() $[(x_n)_n]\in F(A)$. Then
$[(x_n)_n]\in F(A)$. Then ![]() $\tau_{A, \omega}$ is a well-defined tracial state on F(A) by [Reference Nawata28, proposition 2.1]. Put
$\tau_{A, \omega}$ is a well-defined tracial state on F(A) by [Reference Nawata28, proposition 2.1]. Put ![]() $J_{\tau_{A}}:=\{x\in F(A)\; |\; \tau_{A, \omega}(x^*x)=0\}$. If A is separable and τA is faithful, then
$J_{\tau_{A}}:=\{x\in F(A)\; |\; \tau_{A, \omega}(x^*x)=0\}$. If A is separable and τA is faithful, then ![]() $\pi_{\tau_{A}}$ induces an isomorphism from
$\pi_{\tau_{A}}$ induces an isomorphism from ![]() $F(A)/J_{\tau_{A}}$ onto
$F(A)/J_{\tau_{A}}$ onto ![]() $\pi_{\tau_{A}}(A)^{\prime\prime}_{\omega}$ by essentially the same argument as in the proof of [Reference Kirchberg and Rørdam18, theorem 3.3]. In this article, the reindexing argument and the diagonal argument (or Kirchberg’s ɛ-test [Reference Kirchberg17, lemma A.1]) are frequently used. We refer the reader to [Reference Bosa, Brown, Sato, Tikuisis, White and Winter1, Section 1.3] and [Reference Ocneanu32, Chapter 5] for details of these arguments. Every action α of a countable discrete group on A induces an action on F(A). We denote it by the same symbol α for simplicity. Note that if α on A are cocycle conjugate to β on B, then α on F(A) are conjugate to β on F(B). If A is simple, separable, and monotracial, then
$\pi_{\tau_{A}}(A)^{\prime\prime}_{\omega}$ by essentially the same argument as in the proof of [Reference Kirchberg and Rørdam18, theorem 3.3]. In this article, the reindexing argument and the diagonal argument (or Kirchberg’s ɛ-test [Reference Kirchberg17, lemma A.1]) are frequently used. We refer the reader to [Reference Bosa, Brown, Sato, Tikuisis, White and Winter1, Section 1.3] and [Reference Ocneanu32, Chapter 5] for details of these arguments. Every action α of a countable discrete group on A induces an action on F(A). We denote it by the same symbol α for simplicity. Note that if α on A are cocycle conjugate to β on B, then α on F(A) are conjugate to β on F(B). If A is simple, separable, and monotracial, then ![]() $\tilde{\alpha}$ also induces an action on
$\tilde{\alpha}$ also induces an action on ![]() $\pi_{\tau_{A}}(A)^{\prime\prime}_{\omega}$. We also denote it by the same symbol
$\pi_{\tau_{A}}(A)^{\prime\prime}_{\omega}$. We also denote it by the same symbol ![]() $\tilde{\alpha}$. By [Reference Nawata31, proposition 3.9], we see that
$\tilde{\alpha}$. By [Reference Nawata31, proposition 3.9], we see that ![]() $\pi_{\tau_{A}}$ induces an isomorphism from
$\pi_{\tau_{A}}$ induces an isomorphism from  $F(A)^{\alpha}/J_{\tau_{A}}^{\alpha}$ onto
$F(A)^{\alpha}/J_{\tau_{A}}^{\alpha}$ onto  $(\pi_{\tau_{A}}(A)^{\prime\prime})_{\omega}^{\tilde{\alpha}}$.
$(\pi_{\tau_{A}}(A)^{\prime\prime})_{\omega}^{\tilde{\alpha}}$.
The following proposition is an immediate consequence of [Reference Nawata31, theorem 3.6], [Reference Nawata31, proposition 3.11], and [Reference Nawata31, proposition 3.12]. Note that these propositions are based on results in [Reference Matui and Sato25–Reference Matui and Sato27, Reference Sato34–Reference Sato36, Reference Szabó42].
Proposition 2.1. Let α be an outer action of a countable discrete amenable group on ![]() $\mathcal{W}$.
$\mathcal{W}$.
(1) The Razak–Jacelon algebra
 $\mathcal{W}$ has property (SI) relative to α, that is, if a and b are positive contractions in
$\mathcal{W}$ has property (SI) relative to α, that is, if a and b are positive contractions in  $F(\mathcal{W})^{\alpha}$ satisfying
$F(\mathcal{W})^{\alpha}$ satisfying  $\tau_{\mathcal{W}, \omega}(a)=0$ and
$\tau_{\mathcal{W}, \omega}(a)=0$ and  $\inf_{m\in\mathbb{N}}\tau_{\mathcal{W}, \omega}(b^m) \gt 0$, then there exists an element s in
$\inf_{m\in\mathbb{N}}\tau_{\mathcal{W}, \omega}(b^m) \gt 0$, then there exists an element s in  $F(\mathcal{W})^{\alpha}$ such that bs = s and
$F(\mathcal{W})^{\alpha}$ such that bs = s and  $s^*s=a$.
$s^*s=a$.(2) The fixed point algebra
 $F(\mathcal{W})^{\alpha}$ is monotracial.
$F(\mathcal{W})^{\alpha}$ is monotracial.(3) If a and b are positive elements in
 $F(\mathcal{W})^{\alpha}$ satisfying
$F(\mathcal{W})^{\alpha}$ satisfying  $d_{\tau_{\mathcal{W}, \omega}}(a) \lt d_{\tau_{\mathcal{W}, \omega}}(b)$, then there exists an element r in
$d_{\tau_{\mathcal{W}, \omega}}(a) \lt d_{\tau_{\mathcal{W}, \omega}}(b)$, then there exists an element r in  $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that  $r^*br=a$.
$r^*br=a$.
Definition 2.2. Let α be an action of a countable discrete group Γ on ![]() $\mathcal{W}$. We say that α has property W if α satisfies the following properties:
$\mathcal{W}$. We say that α has property W if α satisfies the following properties:
(i) there exists a unital
 $*$-homomorphism from
$*$-homomorphism from  $M_{2}(\mathbb{C})$ to
$M_{2}(\mathbb{C})$ to  $F(\mathcal{W})^{\alpha}$,
$F(\mathcal{W})^{\alpha}$,(ii) if x and y are normal elements in
 $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that  $\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and
$\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and  $0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any
$0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any  $f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$, then x and y are unitary equivalent in
$f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$, then x and y are unitary equivalent in  $F(\mathcal{W})^{\alpha}$.
$F(\mathcal{W})^{\alpha}$.
Note that if there exists a unital ![]() $*$-homomorphism from
$*$-homomorphism from ![]() $M_{2}(\mathbb{C})$ to
$M_{2}(\mathbb{C})$ to ![]() $F(\mathcal{W})^{\alpha}$, then α on
$F(\mathcal{W})^{\alpha}$, then α on ![]() $\mathcal{W}$ is cocycle conjugate to
$\mathcal{W}$ is cocycle conjugate to ![]() $\alpha\otimes\mathrm{id}_{M_{2^{\infty}}}$ on
$\alpha\otimes\mathrm{id}_{M_{2^{\infty}}}$ on ![]() $\mathcal{W}\otimes M_{2^{\infty}}$. Indeed, there exists a unital
$\mathcal{W}\otimes M_{2^{\infty}}$. Indeed, there exists a unital ![]() $*$-homomorphism from
$*$-homomorphism from ![]() $M_{2^{\infty}}$ to
$M_{2^{\infty}}$ to ![]() $F(\mathcal{W})^{\alpha}$ by a similar argument as [Reference Kirchberg17, corollary 1.13]. Hence [Reference Szabó38, corollary 3.8] (see also [Reference Szabó41]) implies this cocycle conjugacy. Using this observation, proposition 2.1 and definition 2.2 instead of
$F(\mathcal{W})^{\alpha}$ by a similar argument as [Reference Kirchberg17, corollary 1.13]. Hence [Reference Szabó38, corollary 3.8] (see also [Reference Szabó41]) implies this cocycle conjugacy. Using this observation, proposition 2.1 and definition 2.2 instead of ![]() $M_{2^{\infty}}$-stability of
$M_{2^{\infty}}$-stability of ![]() $\mathcal{W}$, [Reference Nawata28, proposition 4.1], [Reference Nawata28, theorem 5.3], and [Reference Nawata28, theorem 5.8], we obtain the following theorem by essentially the same arguments as in the proofs of [Reference Nawata28, proposition 4.2], [Reference Nawata28, theorem 5.7], and [Reference Nawata28, corollary 5.11] (or [Reference Nawata29, corollary 5.5]).
$\mathcal{W}$, [Reference Nawata28, proposition 4.1], [Reference Nawata28, theorem 5.3], and [Reference Nawata28, theorem 5.8], we obtain the following theorem by essentially the same arguments as in the proofs of [Reference Nawata28, proposition 4.2], [Reference Nawata28, theorem 5.7], and [Reference Nawata28, corollary 5.11] (or [Reference Nawata29, corollary 5.5]).
Theorem 2.3 Let α be an outer action of a countable discrete amenable group on ![]() $\mathcal{W}$. Assume that α has property W.
$\mathcal{W}$. Assume that α has property W.
(1) For any
 $\theta\in [0,1]$, there exists a projection p in
$\theta\in [0,1]$, there exists a projection p in  $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that  $\tau_{\mathcal{W}, \omega}(p)=\theta$.
$\tau_{\mathcal{W}, \omega}(p)=\theta$.(2) For any unitary element u in
 $F(\mathcal{W})^{\alpha}$, there exists a continuous path of unitaries
$F(\mathcal{W})^{\alpha}$, there exists a continuous path of unitaries  $U: [0,1]\to F(\mathcal{W})^{\alpha}$ such that
$U: [0,1]\to F(\mathcal{W})^{\alpha}$ such that
 \begin{equation*}
U(0)=1,\quad U(1)=u \quad \text{and} \quad \mathrm{Lip}(U)\leq 2\pi
\end{equation*}
\begin{equation*}
U(0)=1,\quad U(1)=u \quad \text{and} \quad \mathrm{Lip}(U)\leq 2\pi
\end{equation*}where
 $\mathrm{Lip}(U)$ is the Lipschitz constant of U, that is, the smallest positive number satisfying
$\mathrm{Lip}(U)$ is the Lipschitz constant of U, that is, the smallest positive number satisfying  $\| U(t)- U(s)\| \leq \mathrm{Lip}(U)|t-s|$ for any
$\| U(t)- U(s)\| \leq \mathrm{Lip}(U)|t-s|$ for any  $t, s\in [0,1]$.
$t, s\in [0,1]$.(3) If p and q are projections in
 $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that  $0 \lt \tau_{\mathcal{W}, \omega}(p)=\tau_{\mathcal{W}, \omega}(q)$, then p and q are Murray–von Neumann equivalent.
$0 \lt \tau_{\mathcal{W}, \omega}(p)=\tau_{\mathcal{W}, \omega}(q)$, then p and q are Murray–von Neumann equivalent.
For any countable discrete group Γ, let ![]() $\mu^{\Gamma}$ be the Bernoulli shift action of Γ on
$\mu^{\Gamma}$ be the Bernoulli shift action of Γ on  $\bigotimes_{g\in \Gamma}M_{2^{\infty}}\cong M_{2^{\infty}}$. The following theorem is a slight variant of [Reference Nawata31, theorem 8.1]. Note that one of the main techniques in the proof of [Reference Nawata31, theorem 8.1] is Szabó’s approximate cocycle intertwining argument [Reference Szabó43] (see also [Reference Elliott5]).
$\bigotimes_{g\in \Gamma}M_{2^{\infty}}\cong M_{2^{\infty}}$. The following theorem is a slight variant of [Reference Nawata31, theorem 8.1]. Note that one of the main techniques in the proof of [Reference Nawata31, theorem 8.1] is Szabó’s approximate cocycle intertwining argument [Reference Szabó43] (see also [Reference Elliott5]).
Theorem 2.4 Let α be a strongly outer action of a countable discrete amenable group Γ on ![]() $\mathcal{W}$. Then α is cocycle conjugate to
$\mathcal{W}$. Then α is cocycle conjugate to ![]() $\mu^{\Gamma}\otimes\mathrm{id}_{\mathcal{W}}$ on
$\mu^{\Gamma}\otimes\mathrm{id}_{\mathcal{W}}$ on ![]() $M_{2^{\infty}}\otimes \mathcal{W}$ if and only if α has property W and there exists an injective
$M_{2^{\infty}}\otimes \mathcal{W}$ if and only if α has property W and there exists an injective ![]() $*$-homomorphism from
$*$-homomorphism from ![]() $\mathcal{W}\rtimes_{\alpha}\Gamma$ to
$\mathcal{W}\rtimes_{\alpha}\Gamma$ to ![]() $\mathcal{W}$.
$\mathcal{W}$.
Proof. [Reference Nawata31, proposition 4.2], [Reference Nawata31, theorem 4.5], and [Reference Nawata31, theorem 8.1] imply the only if part. The if part is an immediate consequence of [Reference Nawata31, theorem 8.1] and theorem 2.3.
3. First cohomology vanishing type theorem
In this section, we shall show a first cohomology vanishing type theorem (corollary 3.4). This is a corollary of a Rohlin type theorem (theorem 3.3).
The following lemma is well-known among experts. See, for example, [Reference Katayama16, theorem 4.8] for a similar (but not the same) result. For the reader’s convenience, we shall give a proof based on Ocneanu’s classification theorem [Reference Ocneanu32, corollary 1.4].
Lemma 3.1. Let Γ be a countable discrete amenable group, and let N be a normal subgroup of Γ. If γ is an outer action of Γ on the injective II1 factor ![]() $\mathcal{R}_0$ and
$\mathcal{R}_0$ and ![]() $g_0\notin N$, then
$g_0\notin N$, then ![]() $\gamma_{g_0}$ induces a properly outer automorphism of
$\gamma_{g_0}$ induces a properly outer automorphism of  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$.
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$.
Proof. Since N is a normal subgroup, it is clear that ![]() $\gamma_{g_0}$ induces an automorphism of
$\gamma_{g_0}$ induces an automorphism of  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. First, we shall show that
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. First, we shall show that ![]() $\gamma_{g_0}$ is not trivial as an automorphism of
$\gamma_{g_0}$ is not trivial as an automorphism of  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. Let π be the quotient map from Γ to
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. Let π be the quotient map from Γ to ![]() $\Gamma/ N$, and let β be the Bernoulli shift action of
$\Gamma/ N$, and let β be the Bernoulli shift action of ![]() $\Gamma /N$ on
$\Gamma /N$ on  $\mathcal{R}_0\cong \bigotimes_{\pi (g)\in \Gamma /N}\mathcal{R}_0$. Define an action δ of Γ on
$\mathcal{R}_0\cong \bigotimes_{\pi (g)\in \Gamma /N}\mathcal{R}_0$. Define an action δ of Γ on ![]() $\mathcal{R}_0\cong \mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0}$ by
$\mathcal{R}_0\cong \mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0}$ by ![]() $\delta_g:= \gamma_g\otimes \beta_{\pi (g)}$ for any
$\delta_g:= \gamma_g\otimes \beta_{\pi (g)}$ for any ![]() $g\in\Gamma$. By Ocneanu’s classification theorem [Reference Ocneanu32, corollary 1.4], γ on
$g\in\Gamma$. By Ocneanu’s classification theorem [Reference Ocneanu32, corollary 1.4], γ on ![]() $\mathcal{R}_0$ and δ on
$\mathcal{R}_0$ and δ on ![]() $\mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0}$ are cocycle conjugate. Hence there exists an isomorphism Φ from
$\mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0}$ are cocycle conjugate. Hence there exists an isomorphism Φ from ![]() $(\mathcal{R}_0)_{\omega}$ onto
$(\mathcal{R}_0)_{\omega}$ onto ![]() $(\mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0})_{\omega}$ such that
$(\mathcal{R}_0 \bar{\otimes}\mathcal{R}_{0})_{\omega}$ such that ![]() $\Phi\circ \gamma_g=\delta_g\circ \Phi$ for any
$\Phi\circ \gamma_g=\delta_g\circ \Phi$ for any ![]() $g\in \Gamma$. Since
$g\in \Gamma$. Since ![]() $\beta_{\pi (g_0)}$ is an outer automorphism of
$\beta_{\pi (g_0)}$ is an outer automorphism of ![]() $\mathcal{R}_0$, there exists an element
$\mathcal{R}_0$, there exists an element ![]() $(x_n)_n$ in
$(x_n)_n$ in ![]() $(\mathcal{R}_0)_{\omega}$ such that
$(\mathcal{R}_0)_{\omega}$ such that ![]() $(\beta_{\pi(g_0)}(x_n))_n\neq (x_n)_n$ by [Reference Connes4, theorem 3.2]. Put
$(\beta_{\pi(g_0)}(x_n))_n\neq (x_n)_n$ by [Reference Connes4, theorem 3.2]. Put ![]() $(y_n)_n:=\Phi^{-1}((1\otimes x_n)_n)\in (\mathcal{R}_0)_{\omega}$. Then it is easy to see that we have
$(y_n)_n:=\Phi^{-1}((1\otimes x_n)_n)\in (\mathcal{R}_0)_{\omega}$. Then it is easy to see that we have  $(y_n)_n\in (\mathcal{R}_0)_{\omega}^{\gamma|_N}$ and
$(y_n)_n\in (\mathcal{R}_0)_{\omega}^{\gamma|_N}$ and ![]() $(\gamma_{g_0}(y_n))_n\neq (y_n)_n$. Finally, we shall show that
$(\gamma_{g_0}(y_n))_n\neq (y_n)_n$. Finally, we shall show that ![]() $\gamma_{g_0}$ is properly outer as an automorphism of
$\gamma_{g_0}$ is properly outer as an automorphism of  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. Since
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. Since  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$ is a factor (see, for example, [Reference Matui and Sato26, lemma 4.1]), it is enough to show that
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$ is a factor (see, for example, [Reference Matui and Sato26, lemma 4.1]), it is enough to show that ![]() $\gamma_{g_0}$ is outer as an automorphism of
$\gamma_{g_0}$ is outer as an automorphism of  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. In particular, we shall show that for any element
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$. In particular, we shall show that for any element ![]() $(u_n)_n$ in
$(u_n)_n$ in  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$, there exists an element
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$, there exists an element ![]() $(z_n)_n$ in
$(z_n)_n$ in  $(\mathcal{R}_0)_{\omega}^{\gamma|_N}$ such that
$(\mathcal{R}_0)_{\omega}^{\gamma|_N}$ such that ![]() $(u_nz_n)_n=(z_nu_n)_n$ and
$(u_nz_n)_n=(z_nu_n)_n$ and ![]() $(\gamma_{g_0}(z_n))_n\neq (z_n)_n$. Taking a suitable subsequence of
$(\gamma_{g_0}(z_n))_n\neq (z_n)_n$. Taking a suitable subsequence of ![]() $(y_n)_n$ (or the reindexing argument), we obtain the desired element
$(y_n)_n$ (or the reindexing argument), we obtain the desired element ![]() $(z_n)_n$. Consequently, the proof is complete.
$(z_n)_n$. Consequently, the proof is complete.
Consider a semidirect product group ![]() $N\rtimes\mathbb{Z}$. For
$N\rtimes\mathbb{Z}$. For ![]() $g\in N$ and
$g\in N$ and ![]() $m\in\mathbb{Z}$, let (g, m) denote an element in
$m\in\mathbb{Z}$, let (g, m) denote an element in ![]() $N\rtimes \mathbb{Z}$. Note that we have
$N\rtimes \mathbb{Z}$. Note that we have ![]() $N\rtimes \mathbb{Z}=\{(g,m)\; |\; g\in N, m\in\mathbb{Z}\}$. The following lemma is an analogous lemma of [Reference Nawata28, lemma 6.2]. See also [Reference Matui and Sato24, theorem 3.4].
$N\rtimes \mathbb{Z}=\{(g,m)\; |\; g\in N, m\in\mathbb{Z}\}$. The following lemma is an analogous lemma of [Reference Nawata28, lemma 6.2]. See also [Reference Matui and Sato24, theorem 3.4].
Lemma 3.2. Let Γ be a semidirect product ![]() $N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on
$N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. Then for any
$\mathcal{W}$. Then for any ![]() $k\in\mathbb{N}$, there exists a positive contraction f in
$k\in\mathbb{N}$, there exists a positive contraction f in ![]() $F(\mathcal{W})^{\alpha|_{N}}$ such that
$F(\mathcal{W})^{\alpha|_{N}}$ such that
 \begin{equation*}
\tau_{\mathcal{W}, \omega}(f)=\frac{1}{k}\quad \text{and} \quad f\alpha_{(\iota,j)}(f)=0
\end{equation*}
\begin{equation*}
\tau_{\mathcal{W}, \omega}(f)=\frac{1}{k}\quad \text{and} \quad f\alpha_{(\iota,j)}(f)=0
\end{equation*} for any ![]() $1\leq j \leq k-1$.
$1\leq j \leq k-1$.
Proof. Since  $\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime}$ is isomorphic to the injective II1 factor, lemma 3.1 implies that
$\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime}$ is isomorphic to the injective II1 factor, lemma 3.1 implies that ![]() $\tilde{\alpha}_{(\iota, 1)}$ is an aperiodic automorphism of
$\tilde{\alpha}_{(\iota, 1)}$ is an aperiodic automorphism of  $(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$. Hence it follows from [Reference Connes3, theorem 1.2.5] that there exists a partition of unity
$(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$. Hence it follows from [Reference Connes3, theorem 1.2.5] that there exists a partition of unity  $\{P_{j}\}_{j=1}^k$ consisting of projections in
$\{P_{j}\}_{j=1}^k$ consisting of projections in  $(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ such that
$(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ such that ![]() $\tilde{\alpha}_{(\iota, 1)}(P_{j})=P_{j+1}$ for any
$\tilde{\alpha}_{(\iota, 1)}(P_{j})=P_{j+1}$ for any ![]() $1\leq j \leq k-1$. Since
$1\leq j \leq k-1$. Since ![]() $\pi_{\tau_{\mathcal{W}}}$ induces an isomorphism from
$\pi_{\tau_{\mathcal{W}}}$ induces an isomorphism from  $F(\mathcal{W})^{\alpha|_N}/J_{\tau_{\mathcal{W}}}^{\alpha|_N}$ onto
$F(\mathcal{W})^{\alpha|_N}/J_{\tau_{\mathcal{W}}}^{\alpha|_N}$ onto  $(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ (see §2.2), there exists a positive contraction
$(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ (see §2.2), there exists a positive contraction ![]() $[(e_n)_n]$ in
$[(e_n)_n]$ in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that ![]() $(\pi_{\tau_{\mathcal{W}}}(e_n))_n=P_1$ in
$(\pi_{\tau_{\mathcal{W}}}(e_n))_n=P_1$ in  $(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$. Then we have
$(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$. Then we have
 \begin{equation*}
\lim_{n\to\omega} \| \pi_{\tau_{\mathcal{W}}}(e_n \alpha_{(\iota ,j)}(e_n))\|_2=0
\quad
\text{and}
\quad
\tau_{\mathcal{W}, \omega}([(e_n)_n])=\tilde{\tau}_{\mathcal{W}, \omega}(P_1)=\dfrac{1}{k}
\end{equation*}
\begin{equation*}
\lim_{n\to\omega} \| \pi_{\tau_{\mathcal{W}}}(e_n \alpha_{(\iota ,j)}(e_n))\|_2=0
\quad
\text{and}
\quad
\tau_{\mathcal{W}, \omega}([(e_n)_n])=\tilde{\tau}_{\mathcal{W}, \omega}(P_1)=\dfrac{1}{k}
\end{equation*} for any ![]() $1\leq j \leq k-1$, where
$1\leq j \leq k-1$, where ![]() $\tilde{\tau}_{\mathcal{W}, \omega}$ is the induced tracial state on
$\tilde{\tau}_{\mathcal{W}, \omega}$ is the induced tracial state on  $(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ by
$(\pi_{\tau_{\mathcal{W}}}(\mathcal{W})^{\prime\prime})_{\omega}^{\tilde{\alpha}|_N}$ by ![]() $\tau_{\mathcal{W}}$. The rest of the proof is the same as [Reference Nawata28, lemma 6.2]. (See also [Reference Matui and Sato24, proposition 3.3].)
$\tau_{\mathcal{W}}$. The rest of the proof is the same as [Reference Nawata28, lemma 6.2]. (See also [Reference Matui and Sato24, proposition 3.3].)
Using proposition 2.1, theorem 2.3 (we need to assume that ![]() $\alpha|_N$ has property W), and lemma 3.2 instead of [Reference Nawata28, proposition 4.1], [Reference Nawata28, proposition 4.2], [Reference Nawata28, theorem 5.8], and [Reference Nawata28, lemma 6.2], we obtain the following Rohlin type theorem by essentially the same arguments in the proofs of [Reference Nawata28, lemma 6.3] and [Reference Nawata28, theorem 6.4]. Note that these arguments are based on [Reference Kishimoto19] and [Reference Kishimoto20].
$\alpha|_N$ has property W), and lemma 3.2 instead of [Reference Nawata28, proposition 4.1], [Reference Nawata28, proposition 4.2], [Reference Nawata28, theorem 5.8], and [Reference Nawata28, lemma 6.2], we obtain the following Rohlin type theorem by essentially the same arguments in the proofs of [Reference Nawata28, lemma 6.3] and [Reference Nawata28, theorem 6.4]. Note that these arguments are based on [Reference Kishimoto19] and [Reference Kishimoto20].
Theorem 3.3 Let Γ be a semidirect product ![]() $N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on
$N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. Assume that
$\mathcal{W}$. Assume that ![]() $\alpha|_{N}$ has property W. Then for any
$\alpha|_{N}$ has property W. Then for any ![]() $k\in\mathbb{N}$, there exists a partition on unity
$k\in\mathbb{N}$, there exists a partition on unity  $\{p_{1,i}\}_{i=0}^{k-1}\cup
\{p_{2,j}\}_{j=0}^{k}$ consisting of projections in
$\{p_{1,i}\}_{i=0}^{k-1}\cup
\{p_{2,j}\}_{j=0}^{k}$ consisting of projections in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that
for any ![]() $0\leq i\leq k-2$ and
$0\leq i\leq k-2$ and ![]() $0\leq j\leq k-1$.
$0\leq j\leq k-1$.
Theorem 2.3, theorem 3.3, and Herman–Ocneanu’s argument [Reference Herman and Ocneanu9, theorem 1] (see also remarks after [Reference Herman and Ocneanu9, lemma 1] and [Reference Izumi10, Reference Kishimoto21]) imply the following corollary.
Corollary 3.4. Let Γ be a semidirect product ![]() $N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on
$N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. Assume that
$\mathcal{W}$. Assume that ![]() $\alpha|_{N}$ has property W and S is a countable subset in
$\alpha|_{N}$ has property W and S is a countable subset in ![]() $F(\mathcal{W})^{\alpha|_N}$. For any unitary element u in
$F(\mathcal{W})^{\alpha|_N}$. For any unitary element u in ![]() $F(\mathcal{W})^{\alpha|_N}\cap S^{\prime}$, there exists a unitary element v in
$F(\mathcal{W})^{\alpha|_N}\cap S^{\prime}$, there exists a unitary element v in ![]() $F(\mathcal{W})^{\alpha|_N}\cap S^{\prime}$ such that
$F(\mathcal{W})^{\alpha|_N}\cap S^{\prime}$ such that ![]() $u=v\alpha_{(\iota, 1)}(v)^{*}$.
$u=v\alpha_{(\iota, 1)}(v)^{*}$.
4. Main theorem
In this section, we shall show the main theorem. Recall that ![]() $\mathfrak{C}$ is the smallest class of countable discrete groups with the following properties: (i)
$\mathfrak{C}$ is the smallest class of countable discrete groups with the following properties: (i) ![]() $\mathfrak{C}$ contains the trivial group, (ii)
$\mathfrak{C}$ contains the trivial group, (ii) ![]() $\mathfrak{C}$ is closed under isomorphisms, countable increasing unions and extensions by
$\mathfrak{C}$ is closed under isomorphisms, countable increasing unions and extensions by ![]() $\mathbb{Z}$. Note that if Γ is an extension of N by
$\mathbb{Z}$. Note that if Γ is an extension of N by ![]() $\mathbb{Z}$, then Γ is isomorphic to a semidirect product
$\mathbb{Z}$, then Γ is isomorphic to a semidirect product ![]() $N\rtimes\mathbb{Z}$.
$N\rtimes\mathbb{Z}$.
The following lemma is an easy consequence of the definition of property W and the diagonal argument.
Lemma 4.1. Let Γ be an increasing union ![]() $\bigcup_{m\in\mathbb{N}}\Gamma_m$ of discrete countable groups
$\bigcup_{m\in\mathbb{N}}\Gamma_m$ of discrete countable groups ![]() $\Gamma_m$, and let α be an action of Γ on
$\Gamma_m$, and let α be an action of Γ on ![]() $\mathcal{W}$. If
$\mathcal{W}$. If ![]() $\alpha|_{\Gamma_m}$ has property W for any
$\alpha|_{\Gamma_m}$ has property W for any ![]() $m\in\mathbb{N}$, then α has property W.
$m\in\mathbb{N}$, then α has property W.
The following lemma is an application of corollary 3.4.
Lemma 4.2. Let Γ be a semidirect product ![]() $N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on
$N\rtimes \mathbb{Z}$ where N is a countable discrete amenable group, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. If
$\mathcal{W}$. If ![]() $\alpha|_{N}$ has property W, then α has property W.
$\alpha|_{N}$ has property W, then α has property W.
Proof. (i) There exists a unital ![]() $*$-homomorphism φ from
$*$-homomorphism φ from ![]() $M_{2}(\mathbb{C})$ to
$M_{2}(\mathbb{C})$ to ![]() $F(\mathcal{W})^{\alpha|_N}$ by the assumption. Let
$F(\mathcal{W})^{\alpha|_N}$ by the assumption. Let  $\{e_{ij}\}_{i,j=1}^{2}$ be the standard matrix units of
$\{e_{ij}\}_{i,j=1}^{2}$ be the standard matrix units of ![]() $M_{2}(\mathbb{C})$. Since we have
$M_{2}(\mathbb{C})$. Since we have ![]() $0 \lt \tau_{\mathcal{W}, \omega}(\varphi(e_{11}))
=\tau_{\mathcal{W}, \omega}(\alpha_{(\iota,1)}(\varphi(e_{11})))$, there exists an element w in
$0 \lt \tau_{\mathcal{W}, \omega}(\varphi(e_{11}))
=\tau_{\mathcal{W}, \omega}(\alpha_{(\iota,1)}(\varphi(e_{11})))$, there exists an element w in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that ![]() $w^*w
=\alpha_{(\iota, 1)}(\varphi(e_{11}))$ and
$w^*w
=\alpha_{(\iota, 1)}(\varphi(e_{11}))$ and ![]() $ww^*=\varphi(e_{11})$ by theorem 2.3. Put
$ww^*=\varphi(e_{11})$ by theorem 2.3. Put  $u:= \sum_{i=1}^{2}\varphi(e_{i1})w\alpha_{(\iota ,1)}(\varphi(e_{1i}))$. Then u is a unitary element in
$u:= \sum_{i=1}^{2}\varphi(e_{i1})w\alpha_{(\iota ,1)}(\varphi(e_{1i}))$. Then u is a unitary element in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that ![]() $\alpha_{(\iota, 1)}(\varphi(x))=u^*\varphi(x)u$ for any
$\alpha_{(\iota, 1)}(\varphi(x))=u^*\varphi(x)u$ for any ![]() $x\in M_{2}(\mathbb{C})$. By corollary 3.4, there exists a unitary element v in
$x\in M_{2}(\mathbb{C})$. By corollary 3.4, there exists a unitary element v in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that ![]() $u=v\alpha_{(\iota ,1)}(v)^*$. We have
$u=v\alpha_{(\iota ,1)}(v)^*$. We have ![]() $\alpha_{(\iota, 1)}(v^*\varphi(x)v)= v^*\varphi(x)v$ for any
$\alpha_{(\iota, 1)}(v^*\varphi(x)v)= v^*\varphi(x)v$ for any ![]() $x\in M_{2}(\mathbb{C})$. Hence the map ψ defined by
$x\in M_{2}(\mathbb{C})$. Hence the map ψ defined by ![]() $\psi(x):=v^*\varphi(x)v$ for any
$\psi(x):=v^*\varphi(x)v$ for any ![]() $x\in M_{2}(\mathbb{C})$ is a unital
$x\in M_{2}(\mathbb{C})$ is a unital ![]() $*$-homomorphism from
$*$-homomorphism from ![]() $M_{2}(\mathbb{C})$ to
$M_{2}(\mathbb{C})$ to ![]() $F(\mathcal{W})^{\alpha}$. (ii) Let x and y be normal elements in
$F(\mathcal{W})^{\alpha}$. (ii) Let x and y be normal elements in ![]() $F(\mathcal{W})^{\alpha}$ such that
$F(\mathcal{W})^{\alpha}$ such that ![]() $\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and
$\mathrm{Sp}(x)=\mathrm{Sp}(y)$ and ![]() $0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any
$0 \lt \tau_{\mathcal{W}, \omega} (f(x))=\tau_{\mathcal{W}, \omega}(f(y))$ for any ![]() $f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$. Since x and y are also elements in
$f\in C(\mathrm{Sp}(x))_{+}\setminus\{0\}$. Since x and y are also elements in ![]() $F(\mathcal{W})^{\alpha|_N}$, there exists a unitary element u in
$F(\mathcal{W})^{\alpha|_N}$, there exists a unitary element u in ![]() $F(\mathcal{W})^{\alpha|_N}$ such that
$F(\mathcal{W})^{\alpha|_N}$ such that ![]() $uxu^*=y$ by the assumption. Note that
$uxu^*=y$ by the assumption. Note that ![]() $u\alpha_{(\iota, 1)}(u)^*$ is a unitary element in
$u\alpha_{(\iota, 1)}(u)^*$ is a unitary element in ![]() $F(\mathcal{W})^{\alpha|_N}\cap \{y\}^{\prime}$. Hence corollary 3.4 implies that there exists a unitary element v in
$F(\mathcal{W})^{\alpha|_N}\cap \{y\}^{\prime}$. Hence corollary 3.4 implies that there exists a unitary element v in ![]() $F(\mathcal{W})^{\alpha|_N}\cap \{y\}^{\prime}$ such that
$F(\mathcal{W})^{\alpha|_N}\cap \{y\}^{\prime}$ such that ![]() $u\alpha_{(\iota, 1)}(u)^*=v\alpha_{(\iota, 1)}(v)^*$. We have
$u\alpha_{(\iota, 1)}(u)^*=v\alpha_{(\iota, 1)}(v)^*$. We have ![]() $\alpha_{(\iota ,1)}(v^*u)=v^*u$ and
$\alpha_{(\iota ,1)}(v^*u)=v^*u$ and ![]() $v^*uxu^*v= v^*yv=y$. Therefore, x and y are unitary equivalent in
$v^*uxu^*v= v^*yv=y$. Therefore, x and y are unitary equivalent in ![]() $F(\mathcal{W})^{\alpha}$. By (i) and (ii), α has property W.
$F(\mathcal{W})^{\alpha}$. By (i) and (ii), α has property W.
The following theorem is the main theorem in this article.
Theorem 4.3 Let Γ be a countable discrete group in ![]() $\mathfrak{C}$, and let α be a strongly outer action of Γ on
$\mathfrak{C}$, and let α be a strongly outer action of Γ on ![]() $\mathcal{W}$. Then α is cocycle conjugate to
$\mathcal{W}$. Then α is cocycle conjugate to ![]() $\mu^{\Gamma}\otimes \mathrm{id}_{\mathcal{W}}$ on
$\mu^{\Gamma}\otimes \mathrm{id}_{\mathcal{W}}$ on ![]() $M_{2^{\infty}}\otimes\mathcal{W}$.
$M_{2^{\infty}}\otimes\mathcal{W}$.
Proof. Every action of the trivial group on ![]() $\mathcal{W}$ has property W by results in [Reference Nawata28] (or [Reference Nawata30, theorem 3.8]). By lemmas 4.1 and 4.2, we see that α has property W. Note that this implies that
$\mathcal{W}$ has property W by results in [Reference Nawata28] (or [Reference Nawata30, theorem 3.8]). By lemmas 4.1 and 4.2, we see that α has property W. Note that this implies that ![]() $\mathcal{W}\rtimes_{\alpha}\Gamma$ is
$\mathcal{W}\rtimes_{\alpha}\Gamma$ is ![]() $M_{2^{\infty}}$-stable because α is cocycle conjugate to
$M_{2^{\infty}}$-stable because α is cocycle conjugate to ![]() $\alpha\otimes\mathrm{id}_{M_{2^{\infty}}}$ on
$\alpha\otimes\mathrm{id}_{M_{2^{\infty}}}$ on ![]() $\mathcal{W}\otimes M_{2^{\infty}}$. Since the class of separable nuclear C
$\mathcal{W}\otimes M_{2^{\infty}}$. Since the class of separable nuclear C![]() $^*$-algebras that are KK-equivalent to
$^*$-algebras that are KK-equivalent to ![]() $\{0\}$ is closed under countable inductive limits and crossed products by
$\{0\}$ is closed under countable inductive limits and crossed products by ![]() $\mathbb{Z}$, [Reference Nawata30, theorem 6.1] implies that
$\mathbb{Z}$, [Reference Nawata30, theorem 6.1] implies that ![]() $\mathcal{W}\rtimes_{\alpha}\Gamma$ is isomorphic to
$\mathcal{W}\rtimes_{\alpha}\Gamma$ is isomorphic to ![]() $\mathcal{W}$. Therefore, we obtain the conclusion by theorem 2.4.
$\mathcal{W}$. Therefore, we obtain the conclusion by theorem 2.4.
The following corollary is an immediate consequence of the theorem above.
Corollary 4.4. Let Γ be a countable discrete group in ![]() $\mathfrak{C}$. Then there exists a unique strongly outer action of Γ on
$\mathfrak{C}$. Then there exists a unique strongly outer action of Γ on ![]() $\mathcal{W}$ up to cocycle conjugacy.
$\mathcal{W}$ up to cocycle conjugacy.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 20K03630.