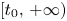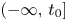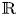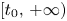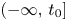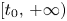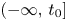1. Introduction
The well-established notion of exponential dichotomy used in the analysis of nonautonomous systems essentially originated from the work of Perron [Reference Perron41]. The theory of exponential dichotomy is a powerful tool to describe hyperbolicity of dynamical systems generated by differential equations, especially for the stable and unstable invariant manifolds of time-dependent systems. As mentioned in Coppel [Reference Coppel12], ‘that dichotomies, rather than Lyapunov's characteristic exponents, are the key to questions of asymptotic behaviour for nonautonomous differential equations’.
Over the years, the classical exponential dichotomy and its properties have been established for evolution equations [Reference Huy24, Reference Latushkin, Randolph and Schnaubelt30, Reference Palmer40, Reference Preda, Pogan and Preda47–Reference Sacker and Sell49], functional differential equations [Reference Coffman and Schäffer11, Reference Lin31, Reference Pecelli42], skew-product flows [Reference Chow and Leiva9, Reference Chow and Leiva10, Reference Latushkin, Montgomery-Smith and Randolph29, Reference Sacker and Sell50] and random systems or stochastic equations [Reference Doan, Rasmussen and Kloeden14, Reference Stoica53, Reference Zhou, Lu and Zhang54, Reference Zhu and Jiang58, Reference Zhu, Chu and Zhang59]. We also refer to the books [Reference Chicone and Latushkin8, Reference Coppel12, Reference Massera and Schäffer36] for details and further references related to exponential dichotomies.
However, dynamical systems exhibit various different kinds of dichotomic behaviour and the classical notion of exponential dichotomy substantially restricts some dynamics. In order to investigate more general hyperbolicity, many attempts (see e.g. [Reference Naulin and Pinto37, Reference Naulin and Pinto38, Reference Preda, Pogan and Preda46]) have been made to extend the concept of classical dichotomies. Inspired by the work of Barreira and Pesin on the notion of nonuniformly hyperbolic trajectory [Reference Barreira and Pesin1, Reference Barreira and Pesin2], Barreira and Valls extended the concept of exponential dichotomy to the nonuniform ones and investigated some related problems, see for examples, the works [Reference Barreira, Chu and Valls3–Reference Barreira and Valls7] and the references therein.
On the other hand, from the point of view of Itô stochastic differential equations (SDE), such properties of mean-square are natural since the Itô stochastic calculus is essentially deterministic in the mean-square setting, and there exist stationary coordinate changes under which flows of nonautonomous random differential equation can be viewed as those of SDE [Reference Imkeller and Lederer25]. Some related works on mean-square setting of random systems or stochastic equations can be found in [Reference Fu and Liu17, Reference Higham21–Reference Higham, Mao and Yuan23, Reference Kloeden and Lorenz27, Reference Liu and Sun33, Reference Zhu and Chu57]. To the best of our knowledge, mean-square exponential dichotomy (MS-ED) was first introduced by Stanzhyts'kyi [Reference Stanzhyts'kyi51], in which a sufficient condition has been proved to ensure that a linear SDE satisfies an MS-ED. Based on the definition of MS-ED, Stanzhyts'kyi and Krenevych [Reference Stanzhyts'kyi and Krenevych52] proved the existence of a quadratic form of linear SDE. In [Reference Zhu and Jiang58] the robustness of MS-ED for a linear SDE was established. Stoica [Reference Stoica53] studied stochastic cocycles in Hilbert spaces. Recently, Doan et al. [Reference Doan, Rasmussen and Kloeden14] considered the MS-ED spectrum for random dynamical system.
Now we recall the definition of MS-ED. Consider the following linear $n$![]() -dimensional Itô stochastic system
-dimensional Itô stochastic system
where $I$![]() is either the half line $[t_{0},\,+\infty )$
is either the half line $[t_{0},\,+\infty )$![]() , $(-\infty,\,t_{0}]$
, $(-\infty,\,t_{0}]$![]() or the whole ${\Bbb R}$
or the whole ${\Bbb R}$![]() , and $A(t)=(A_{ij}(t))_{n \times n}$
, and $A(t)=(A_{ij}(t))_{n \times n}$![]() , $G(t)=(G_{ij}(t))_{n \times n}$
, $G(t)=(G_{ij}(t))_{n \times n}$![]() are continuous functions with real entries. Equation (1.1) is said to possess an MS-ED if there exists a linear projection $P(t): L^{2}(\Omega,\, {\Bbb R}^{n}) \rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
are continuous functions with real entries. Equation (1.1) is said to possess an MS-ED if there exists a linear projection $P(t): L^{2}(\Omega,\, {\Bbb R}^{n}) \rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() such that
such that
and positive constants $K,\, \alpha$![]() such that
such that

where $\Phi (t)$![]() is a fundamental matrix solution of (1.1), and $Q(t)={\rm Id}-P(t)$
is a fundamental matrix solution of (1.1), and $Q(t)={\rm Id}-P(t)$![]() is the complementary projection of $P(t)$
is the complementary projection of $P(t)$![]() for each $t\in I$
for each $t\in I$![]() . $I^{2}_{\geq }:=\{(t,\,s)\in I^{2}: t\geq s\}$
. $I^{2}_{\geq }:=\{(t,\,s)\in I^{2}: t\geq s\}$![]() and $I^{2}_{\leq }:=\{(t,\,s)\in I^{2}: t\leq s\}$
and $I^{2}_{\leq }:=\{(t,\,s)\in I^{2}: t\leq s\}$![]() denotes the relations of $s$
denotes the relations of $s$![]() and $t$
and $t$![]() on $I$
on $I$![]() .
.
Inspired by the above, this paper is to study the robustness of NMS-ED. (1.1) is said to possess an NMS-ED if there exists a linear projection $P(t): L^{2}(\Omega,\, {\Bbb R}^{n}) \rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() such that (1.2) holds, and some constants $M,\, \alpha >0$
such that (1.2) holds, and some constants $M,\, \alpha >0$![]() , $\varepsilon \ge 0$
, $\varepsilon \ge 0$![]() such that
such that
where $\Phi (t)$![]() is a fundamental matrix solution of (1.1), $Q(t)={\rm Id}-P(t)$
is a fundamental matrix solution of (1.1), $Q(t)={\rm Id}-P(t)$![]() is the complementary projection of $P(t)$
is the complementary projection of $P(t)$![]() for each $t\in I$
for each $t\in I$![]() . $I^{2}_{\geq }:=\{(t,\,s)\in I^{2}: t\geq s\}$
. $I^{2}_{\geq }:=\{(t,\,s)\in I^{2}: t\geq s\}$![]() and $I^{2}_{\leq }:=\{(t,\,s)\in I^{2}: t\leq s\}$
and $I^{2}_{\leq }:=\{(t,\,s)\in I^{2}: t\leq s\}$![]() denotes the relations of $s$
denotes the relations of $s$![]() and $t$
and $t$![]() on $I$
on $I$![]() . For convenience, the constants $\alpha$
. For convenience, the constants $\alpha$![]() and $K$
and $K$![]() in (1.3)–(1.4) are called the exponent and the bound of the NMS-ED, respectively, as in the case of deterministic systems [Reference Henry20]. $\varepsilon$
in (1.3)–(1.4) are called the exponent and the bound of the NMS-ED, respectively, as in the case of deterministic systems [Reference Henry20]. $\varepsilon$![]() is called the nonuniform degree of the NMS-ED. In particular, while $\varepsilon =0$
is called the nonuniform degree of the NMS-ED. In particular, while $\varepsilon =0$![]() , we obtain the notion of (uniform) MS-ED. We refer to [Reference Stanzhyts'kyi51–Reference Stoica53, Reference Zhu and Chu57–Reference Zhu, Chu and Zhang59] for related results and techniques about this topic.
, we obtain the notion of (uniform) MS-ED. We refer to [Reference Stanzhyts'kyi51–Reference Stoica53, Reference Zhu and Chu57–Reference Zhu, Chu and Zhang59] for related results and techniques about this topic.
It is clear that the notion of NMS-ED is a weaker requirement in comparison to the notion of MS-ED. Actually, there exists a linear SDE which has an NMS-ED with nonuniform degree $\varepsilon$![]() cannot be removed. For example, let $a>b>0$
cannot be removed. For example, let $a>b>0$![]() be real parameters,
be real parameters,
admits an NMS-ED which is not uniform. See example 6.1 in § 6 for details.
Robustness (also known as roughness , see e.g. [Reference Coppel12]) here means that an NMS-ED persists under a sufficiently small linear perturbation. More precisely, for small perturbations $B$![]() , $H$
, $H$![]() , the following linear SDE
, the following linear SDE
also admits an NMS-ED. As indicated by Coppel [Reference Coppel12, p. 28], the robustness of exponential dichotomies was first proved by Massera and Schäffer [Reference Massera and Schäffer36], which states that all ‘neighbouring’ linear systems also have the same dichotomy with a similar projection if the same happens for the original system. Robustness is one of the most basic concepts appearing in the theoretical studies of dynamical systems. This topic plays a key role in the stability theory for dynamical systems. Some early papers about robustness (with the exception of [Reference Coppel12] and [Reference Massera and Schäffer36] mentioned above) are Dalec'kiĭ and Kreĭn [Reference Dalec'kiĭ and Kreĭn13] and Palmer [Reference Palmer39] for ordinary differential equations, Henry [Reference Henry20] and Lin [Reference Lin32] for parabolic partial differential equations, Hale and Lin [Reference Hale and Lin19] and Lizana [Reference Lizana34] for functional differential equations, Pliss and Sell [Reference Pliss and Sell43] and Chow and Leiva [Reference Chow and Leiva10] for skew-product semiflow. For more recent works refer to papers [Reference Barreira, Silva and Valls5, Reference Barreira and Valls7, Reference Ju and Wiggins26, Reference Popescu44, Reference Popescu45, Reference Zhou, Lu and Zhang55, Reference Zhou and Zhang56]. It is worth mentioning that on half line ${\Bbb R}^+$![]() , ${\Bbb R}^{-}$
, ${\Bbb R}^{-}$![]() as well as the whole ${\Bbb R}$
as well as the whole ${\Bbb R}$![]() , Ju and Wiggins [Reference Ju and Wiggins26] and Popescu [Reference Popescu44, Reference Popescu45] considered the case of roughness for exponential dichotomy and analyse their dynamical behaviour; Zhou et al. [Reference Zhou, Lu and Zhang55] discussed the relationship between nonuniform exponential dichotomy and admissibility.
, Ju and Wiggins [Reference Ju and Wiggins26] and Popescu [Reference Popescu44, Reference Popescu45] considered the case of roughness for exponential dichotomy and analyse their dynamical behaviour; Zhou et al. [Reference Zhou, Lu and Zhang55] discussed the relationship between nonuniform exponential dichotomy and admissibility.
In this study, we extend the results and improve the method of [Reference Zhu and Jiang58]. The main differences of our results and those of [Reference Zhu and Jiang58] are as follows:
• In contrast to [Reference Zhu and Jiang58], we extend the case of robustness of MS-ED to the general nonuniform setting. For this purpose, we need to pass from small bounded perturbations of the coefficient matrix to exponentially decaying perturbations.
• In [Reference Zhu and Jiang58], we only consider the case of robustness on the whole line ${\Bbb R}$
 . In the present paper, we prove the robustness of (1.5) on half line $[t_{0},\,+\infty )$
. In the present paper, we prove the robustness of (1.5) on half line $[t_{0},\,+\infty )$ , $(-\infty,\,t_{0}]$
, $(-\infty,\,t_{0}]$ and the whole ${\Bbb R}$
and the whole ${\Bbb R}$ . The proof is much more delicate than that of MS-ED [Reference Zhu and Jiang58]. This is because in different intervals, the different but related explicit expressions of the projections of the ‘exponential growing solutions’ and the ‘exponential decaying solutions’ for the perturbed equation (1.5) need to be determined first.
. The proof is much more delicate than that of MS-ED [Reference Zhu and Jiang58]. This is because in different intervals, the different but related explicit expressions of the projections of the ‘exponential growing solutions’ and the ‘exponential decaying solutions’ for the perturbed equation (1.5) need to be determined first.• Furthermore, in contrast to paper [Reference Zhu and Jiang58], we analyse and compare the results obtained from operators that make up the projections of (1.1) and (1.5) on different intervals (see theorem 3.10 and remark 5.9), and estimate the distance between the solution of (1.1) and the perturbed solution of (1.5) (see theorem 3.11 and remark 3.12).
The remaining part of this paper is organized as follows. The robustness of nonuniform mean-square exponential contraction (NMS-EC) is established in § 2. Section 3 proves the robustness of NMS-ED on half line $[t_{0},\,+\infty )$![]() and analyses that the solution of (1.1) and the perturbed solution of (1.5) are forward asymptotic in the mean-square sense. The robustness under the nonuniform setting on half line $(-\infty,\,t_{0}]$
and analyses that the solution of (1.1) and the perturbed solution of (1.5) are forward asymptotic in the mean-square sense. The robustness under the nonuniform setting on half line $(-\infty,\,t_{0}]$![]() is presented in § 4. Section 5 combines the advantages of the projections on half line $[t_{0},\,+\infty )$
is presented in § 4. Section 5 combines the advantages of the projections on half line $[t_{0},\,+\infty )$![]() and $(-\infty,\,t_{0}]$
and $(-\infty,\,t_{0}]$![]() , and proves the robustness of NMS-ED on the whole ${\Bbb R}$
, and proves the robustness of NMS-ED on the whole ${\Bbb R}$![]() . In addition, the relationship of the projections on $[t_{0},\,+\infty )$
. In addition, the relationship of the projections on $[t_{0},\,+\infty )$![]() , $(-\infty,\,t_{0}]$
, $(-\infty,\,t_{0}]$![]() and ${\Bbb R}$
and ${\Bbb R}$![]() is also discussed in § 5. Finally, an example is given in § 6, which indicates that there exists a linear SDE which admits an NMS-ED but not uniform.
is also discussed in § 5. Finally, an example is given in § 6, which indicates that there exists a linear SDE which admits an NMS-ED but not uniform.
2. Robustness of NMS-EC
In this section we will answer the following question: Does (1.5) admit an NMS-EC if (1.1) admits an NMS-EC while $B,\,~H$![]() is small? That is to say, we consider the robustness of NMS-EC. The following statement is a particular case of NMS-ED with projection $P(t)=Id$
is small? That is to say, we consider the robustness of NMS-EC. The following statement is a particular case of NMS-ED with projection $P(t)=Id$![]() for every $t\in I$
for every $t\in I$![]() . (1.1) is said to admit an NMS-EC if for some constants $M,\, \alpha >0$
. (1.1) is said to admit an NMS-EC if for some constants $M,\, \alpha >0$![]() and $\varepsilon \ge 0$
and $\varepsilon \ge 0$![]() such that
such that
In particular, when $\varepsilon =0$![]() in (2.1), we obtain the notion of uniform mean-square exponential contraction.
in (2.1), we obtain the notion of uniform mean-square exponential contraction.
Throughout this paper, we assume that $(\Omega,\, \mathscr {F},\, \mathbb {P})$![]() is a probability space, $\omega (t)=(\omega _{1}(t),\,\ldots \omega _{n}(t))^{T}$
is a probability space, $\omega (t)=(\omega _{1}(t),\,\ldots \omega _{n}(t))^{T}$![]() is an $n$
is an $n$![]() -dimensional Brownian motion defined on the space $(\Omega,\, \mathscr {F},\, \mathbb {P})$
-dimensional Brownian motion defined on the space $(\Omega,\, \mathscr {F},\, \mathbb {P})$![]() . $\|\cdot \|$
. $\|\cdot \|$![]() is used to denote both the Euclidean vector norm or the matrix norm as appropriate, and $L^{2}(\Omega,\, {\Bbb R}^{n})$
is used to denote both the Euclidean vector norm or the matrix norm as appropriate, and $L^{2}(\Omega,\, {\Bbb R}^{n})$![]() stands for the space of all ${\Bbb R}^{n}$
stands for the space of all ${\Bbb R}^{n}$![]() -valued random variables $x: \Omega \rightarrow {\Bbb R}^{n}$
-valued random variables $x: \Omega \rightarrow {\Bbb R}^{n}$![]() such that
such that
In order to describe the robustness in an explicit form, we present the following theorem, which shows that the NMS-EC is robust under sufficiently small linear perturbations. Here we mention that the NMS-EC considered in this section is in an arbitrary interval $I\subset {\Bbb R}$![]() .
.
Theorem 2.1 Let $A(\cdot ),\, B(\cdot ),\, G(\cdot ),\, H(\cdot )$![]() be $n \times n$
be $n \times n$![]() -matrix continuous functions with real entries such that (1.1) admits an NMS-EC (2.1) with coefficient matrix bounded and perturbation exponential decaying in $I$
-matrix continuous functions with real entries such that (1.1) admits an NMS-EC (2.1) with coefficient matrix bounded and perturbation exponential decaying in $I$![]() , i.e. there exist constants $a,\, b,\, g,\, h>0$
, i.e. there exist constants $a,\, b,\, g,\, h>0$![]() such that
such that
Let $b,\, h$![]() be small enough such that
be small enough such that
Then (1.5) also admits an NMS-EC in $I$![]() with the bound $M$
with the bound $M$![]() replaced by $3M$
replaced by $3M$![]() , and exponent $\alpha$
, and exponent $\alpha$![]() replaced by $-\frac {\alpha }{2}+\frac {3M\tilde {M}}{\alpha }$
replaced by $-\frac {\alpha }{2}+\frac {3M\tilde {M}}{\alpha }$![]() , i.e.
, i.e.
where $\hat {\Phi }(t)$![]() is a fundamental matrix solution of (1.5).
is a fundamental matrix solution of (1.5).
Proof. Write
One can easily verify that $\hat {\Phi }(t,\,s)$![]() is a fundamental matrix solution of (1.5) with $\hat {\Phi }(s,\,s)=Id$
is a fundamental matrix solution of (1.5) with $\hat {\Phi }(s,\,s)=Id$![]() . $L^{2}(\Omega,\, {\Bbb R}^{n})$
. $L^{2}(\Omega,\, {\Bbb R}^{n})$![]() is a Banach space with the norm $({\mathbb {E}} \|x\|^2)^{\frac {1}{2}}$
is a Banach space with the norm $({\mathbb {E}} \|x\|^2)^{\frac {1}{2}}$![]() . The Banach algebra of bounded linear operators on $L^{2}(\Omega,\, {\Bbb R}^{n})$
. The Banach algebra of bounded linear operators on $L^{2}(\Omega,\, {\Bbb R}^{n})$![]() is denoted by $\mathfrak {B}(L^{2}(\Omega,\, {\Bbb R}^{n}))$
is denoted by $\mathfrak {B}(L^{2}(\Omega,\, {\Bbb R}^{n}))$![]() . Now we introduce the space
. Now we introduce the space
with the norm
Clearly, $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() is a Banach space. In order to state our result, we need the following existence and uniqueness lemma.
is a Banach space. In order to state our result, we need the following existence and uniqueness lemma.
Lemma 2.2 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , (1.5) has a unique solution $\hat {\Phi }(t,\,s) \xi _{0}$
, (1.5) has a unique solution $\hat {\Phi }(t,\,s) \xi _{0}$![]() with $\hat {\Phi } \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
with $\hat {\Phi } \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() such that
such that

with $\hat {\Phi }(s,\,s) \xi _{0}=\Phi (s)\Phi ^{-1}(s) \xi _{0}= \xi _{0}$![]() .
.
Proof. In what follows (in order to simplify the presentation), write $\tilde {B}(t)=B(t)-G(t)H(t)$![]() . We first prove that the function $\hat {\Phi }(t,\,s) \xi _{0}$
. We first prove that the function $\hat {\Phi }(t,\,s) \xi _{0}$![]() is a solution of (1.5). Set
is a solution of (1.5). Set

Let $y(t)=\Phi (t)\xi (t)$![]() . Clearly,
. Clearly,
One can easily verify that $\xi (t)$![]() satisfies the differential
satisfies the differential
Since $\Phi (t)$![]() is a fundamental matrix solution of (1.1), it follows from Itô product rule that
is a fundamental matrix solution of (1.1), it follows from Itô product rule that

which means that $y(t)=\hat {\Phi }(t,\,s) \xi _{0}$![]() is a solution of (1.5). This conclusion is consistent with that in [Reference Mao35, theorem 3.3.1] (see also [Reference Ladde and Ladde28, section 2.4.2]).
is a solution of (1.5). This conclusion is consistent with that in [Reference Mao35, theorem 3.3.1] (see also [Reference Ladde and Ladde28, section 2.4.2]).
Now we prove that $\hat {\Phi }$![]() is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Let
. Let

It follows from (2.1), ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$![]() , Cauchy–Schwarz inequality, Itô isometry property of stochastic integrals and the elementary inequality
, Cauchy–Schwarz inequality, Itô isometry property of stochastic integrals and the elementary inequality

that

and this implies that

with $\tilde {M}=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() . Following the same procedure above, for any $\hat {\Phi }_{1},\, \hat {\Phi }_{2}\in \mathscr {L}_{c}$
. Following the same procedure above, for any $\hat {\Phi }_{1},\, \hat {\Phi }_{2}\in \mathscr {L}_{c}$![]() , we have
, we have

Note that

which together with (2.8) implies

Since $\tilde {M}<\frac {\alpha ^{2}}{3M}$![]() , $\Gamma$
, $\Gamma$![]() is a contraction operator. Hence, there exists a unique $\hat {\Phi } \in \mathscr {L}_{c}$
is a contraction operator. Hence, there exists a unique $\hat {\Phi } \in \mathscr {L}_{c}$![]() such that $\Gamma \hat {\Phi }= \hat {\Phi }$
such that $\Gamma \hat {\Phi }= \hat {\Phi }$![]() , which satisfies the identity (2.6). This completes the proof of the lemma.
, which satisfies the identity (2.6). This completes the proof of the lemma.
We proceed with the proof of the theorem. Squaring both sides of (2.6), and taking expectations, it follows from (2.7) that

By using Itô isometry property and inequalities (2.1), the second term of the right-hand side in (2.9) can be deduced as follows:

As to the third term in (2.9), it follows from ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$![]() , Cauchy–Schwarz inequality and the inequalities (2.1) that
, Cauchy–Schwarz inequality and the inequalities (2.1) that

Since $\alpha >0$![]() , we can rewrite inequality (2.9) as
, we can rewrite inequality (2.9) as

Let
for any fixed $s\in I$![]() with $\tilde {M}=\alpha h^{2}+8b^{2}+8g^{2}h^{2}$
with $\tilde {M}=\alpha h^{2}+8b^{2}+8g^{2}h^{2}$![]() . Clearly, inequality (2.10) can be rewritten as
. Clearly, inequality (2.10) can be rewritten as
On the contrary,
and therefore,

Integrating the above inequality from $s$![]() to $t$
to $t$![]() and note that $X(s)=3Me^{\varepsilon |s|}$
and note that $X(s)=3Me^{\varepsilon |s|}$![]() , we obtain
, we obtain
By (2.12), using (2.11), we obtain the desired inequality (2.3), and this completes the proof of the theorem.
Remark 2.3 Since the nonuniform degree $\varepsilon >0$![]() exists for $(t,\,s)\in I^{2}_{\geq }$
exists for $(t,\,s)\in I^{2}_{\geq }$![]() , the perturbations $B$
, the perturbations $B$![]() and $H$
and $H$![]() should be chosen with exponential decaying to eliminate the effect caused by the nonuniform degree. For the uniform case, it suffices to consider the bounded condition instead of exponential decaying. See [Reference Zhu and Jiang58] for details about the case of $\varepsilon =0$
should be chosen with exponential decaying to eliminate the effect caused by the nonuniform degree. For the uniform case, it suffices to consider the bounded condition instead of exponential decaying. See [Reference Zhu and Jiang58] for details about the case of $\varepsilon =0$![]() , which generalizes (and imitates) the notion of robustness of exponential dichotomy for ODE (see e.g. [Reference Coppel12, Reference Massera and Schäffer36]).
, which generalizes (and imitates) the notion of robustness of exponential dichotomy for ODE (see e.g. [Reference Coppel12, Reference Massera and Schäffer36]).
As a special case of (1.5), if we consider the system
in which the linear perturbed term only appears in the ‘drift’. Of course, theorem 2.1 can also be applied to (2.13) but merely with the development of slightly better estimation (with the bound and the exponent replaced by smaller constants) than the one in theorem 2.1, since there is no perturbation in the ‘volatility’. Actually, for any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , (2.13) has a unique solution $\hat {\Phi }(t,\,s) \xi _{0}$
, (2.13) has a unique solution $\hat {\Phi }(t,\,s) \xi _{0}$![]() with $\hat {\Phi } \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
with $\hat {\Phi } \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() such that
such that
instead of (2.6), which is more similar to solutions of the classical ordinary differential equations (see e.g. [Reference Hale18]).
Theorem 2.4 Let $A(\cdot ),\, B(\cdot ),\, G(\cdot )$![]() be $n \times n$
be $n \times n$![]() -matrix continuous functions with real entries such that (1.1) admits an NMS-EC (2.1) with coefficient matrix bounded and perturbation exponential decaying in $I$
-matrix continuous functions with real entries such that (1.1) admits an NMS-EC (2.1) with coefficient matrix bounded and perturbation exponential decaying in $I$![]() , i.e. there exist constants $a,\, b,\, g>0$
, i.e. there exist constants $a,\, b,\, g>0$![]() such that
such that
If $b<\alpha /(2\sqrt {2M})$![]() , then (2.13) also admits an NMS-EC in $I$
, then (2.13) also admits an NMS-EC in $I$![]() with the bound $M$
with the bound $M$![]() replaced by $2M$
replaced by $2M$![]() , and exponent $\alpha$
, and exponent $\alpha$![]() replaced by $-\frac {\alpha }{2}+\frac {4Mb^{2}}{\alpha }$
replaced by $-\frac {\alpha }{2}+\frac {4Mb^{2}}{\alpha }$![]() , i.e.
, i.e.
3. Robustness of NMS-ED on the half line $[t_{0},\,+\infty )$
In this section, we state and prove our main result on the robustness of NMS-ED on $I=[t_{0},\,+\infty )$![]() . The case of the interval $I=(-\infty,\,t_{0}]$
. The case of the interval $I=(-\infty,\,t_{0}]$![]() and the whole ${\Bbb R}$
and the whole ${\Bbb R}$![]() will be discussed in § 4 and § 5, respectively.
will be discussed in § 4 and § 5, respectively.
The following theorem is on the robustness of NMS-ED of (1.1) on $[t_{0},\,+\infty )$![]() , and its proof is more general and complicated than that of theorem 2.1, because we need to find out the explicit expressions of the ‘exponential growing solutions’ and the ‘exponential decaying solutions’ for the perturbed equation (1.5) along with the stable and unstable directions, respectively. To do this, we rewrite the unique solution of (1.5) along the stable direction under a natural condition: boundedness. It is also worth mentioning that the following theorem is also valid for NMS-EC. Indeed, a contraction is a dichotomy with $P(t)=Id$
, and its proof is more general and complicated than that of theorem 2.1, because we need to find out the explicit expressions of the ‘exponential growing solutions’ and the ‘exponential decaying solutions’ for the perturbed equation (1.5) along with the stable and unstable directions, respectively. To do this, we rewrite the unique solution of (1.5) along the stable direction under a natural condition: boundedness. It is also worth mentioning that the following theorem is also valid for NMS-EC. Indeed, a contraction is a dichotomy with $P(t)=Id$![]() for every $t\in I$
for every $t\in I$![]() .
.
Theorem 3.1 Let $A(\cdot ),\, B(\cdot ),\, G(\cdot ),\, H(\cdot )$![]() be $n \times n$
be $n \times n$![]() -matrix continuous functions with real entries such that (1.1) admits an NMS-ED (1.3)–(1.4) with $\varepsilon <\alpha$
-matrix continuous functions with real entries such that (1.1) admits an NMS-ED (1.3)–(1.4) with $\varepsilon <\alpha$![]() , and assume that coefficient matrices of (1.5) satisfy
, and assume that coefficient matrices of (1.5) satisfy
with constants $a,\, b,\, g,\, h>0$![]() . Let $b,\, h$
. Let $b,\, h$![]() be small enough such that
be small enough such that
Then (1.5) admits an NMS-ED in $I$![]() with linear projections $\hat {P}(t): L^{2}(\Omega,\, {\Bbb R}^{n}) \rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
with linear projections $\hat {P}(t): L^{2}(\Omega,\, {\Bbb R}^{n}) \rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() such that
such that
and
where bound $\hat {M}:=40M$![]() , exponent $\hat {\alpha }:=\frac {\alpha }{2}-\frac {10M\tilde {M}}{\alpha }$
, exponent $\hat {\alpha }:=\frac {\alpha }{2}-\frac {10M\tilde {M}}{\alpha }$![]() and nonuniform degree $\hat {\varepsilon }:=2\varepsilon$
and nonuniform degree $\hat {\varepsilon }:=2\varepsilon$![]() .
.
Proof of theorem 3.1. Proof of theorem 3.1
We first prove several lemmas which are essential in proving the theorem. The first one is the existence and uniqueness lemma, which is slightly different from lemma 2.2 since $U(s,\,s)\xi _{0}$![]() is not necessarily equal to $\xi _{0}$
is not necessarily equal to $\xi _{0}$![]() in (3.5). We will explain the reason after lemma 3.7 under which condition there exists an equivalence between (2.6) and (3.5) below.
in (3.5). We will explain the reason after lemma 3.7 under which condition there exists an equivalence between (2.6) and (3.5) below.
Lemma 3.2 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , (1.5) has a unique solution $U(t,\,s) \xi _{0}$
, (1.5) has a unique solution $U(t,\,s) \xi _{0}$![]() with $U \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
with $U \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() such that
such that

Proof. We first prove that the function $U(t,\,s) \xi _{0}$![]() is a solution of (1.5). Set
is a solution of (1.5). Set

Let $y(t)=\Phi (t)\xi (t)$![]() . Clearly,
. Clearly,
and then $\xi (t)$![]() satisfies the differential
satisfies the differential
Since $\Phi (t)$![]() is a fundamental matrix solution of (1.1). it follows from Itô product rule that
is a fundamental matrix solution of (1.1). it follows from Itô product rule that

which means that $y(t)=U(t,\,s) \xi _{0}$![]() is a solution of (1.5).
is a solution of (1.5).
Now we prove that $U$![]() is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Let
. Let

The same idea as in lemma 2.2 can be applied to prove the uniqueness of the solution to (3.5). Squaring both sides of (3.5), and taking expectations, we have

and this implies that

with $\tilde {M}=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() . Following the same procedure as above, for any $U_{1},\, U_{2}\in \mathscr {L}_{c}$
. Following the same procedure as above, for any $U_{1},\, U_{2}\in \mathscr {L}_{c}$![]() , we have
, we have

Note that

which together with (3.6) implies

Since $\tilde {M}<\frac {\alpha ^{2}}{10M}$![]() , $\Gamma$
, $\Gamma$![]() is a contraction operator. Hence, there exists a unique $U \in \mathscr {L}_{c}$
is a contraction operator. Hence, there exists a unique $U \in \mathscr {L}_{c}$![]() such that $\Gamma U= U$
such that $\Gamma U= U$![]() , which satisfies identity (3.5). This completes the proof of the lemma.
, which satisfies identity (3.5). This completes the proof of the lemma.
Lemma 3.3 For any $u\in (s,\,t)$![]() in $I$
in $I$![]() , we have
, we have
in the sense of $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() .
.
Proof. By (1.2) and (3.5) with any $t\ge u \ge s$![]() in $I$
in $I$![]() , we have
, we have

Subtracting (3.5) from (3.7) we obtain

Write $\tilde {U}(t,\,s)=U(t,\,s)-U(t,\,u)U(u,\,s)$![]() . Now we prove $\tilde {U}$
. Now we prove $\tilde {U}$![]() is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is unique in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Let
. Let

Squaring both sides of (3.8), and taking expectations, it follows from (2.7) that

By using the Itô isometry property and inequalities (1.3), the first term on the right-hand side in (3.9) can be deduced as follows:

As for the second term in (3.9), it follows from ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$![]() , Cauchy–Schwarz inequality, Itô isometry property of stochastic integrals and (1.3) that
, Cauchy–Schwarz inequality, Itô isometry property of stochastic integrals and (1.3) that

Clearly, the proof above is also valid for proving the other terms on the right-hand side in (3.9). Thus, we can rewrite inequality (3.9) as

and

with $\tilde {M}=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() . Following the same procedure as above, for any $\tilde {U}_{1},\, \tilde {U}_{2}\in \mathscr {L}_{c}$
. Following the same procedure as above, for any $\tilde {U}_{1},\, \tilde {U}_{2}\in \mathscr {L}_{c}$![]() , we have
, we have

Since $\tilde {M}<\frac {\alpha ^{2}}{8M}$![]() , this implies $\mathcal {T}$
, this implies $\mathcal {T}$![]() is a contraction. Hence, there is a unique $\tilde {U}\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
is a contraction. Hence, there is a unique $\tilde {U}\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Besides, $0\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
. Besides, $0\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() also satisfies (3.8). Hence, we must have
also satisfies (3.8). Hence, we must have
in $\mathscr {L}_{c}$![]() . Therefore, $U(t,\,s)=U(t,\,u)U(u,\,s)$
. Therefore, $U(t,\,s)=U(t,\,u)U(u,\,s)$![]() with $U \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
with $U \in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . This completes the proof of the lemma.
. This completes the proof of the lemma.
Lemma 3.4 Given $s\in I$![]() , if $y(t):=\Lambda (t,\,s) \xi :[s,\,+\infty )\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
, if $y(t):=\Lambda (t,\,s) \xi :[s,\,+\infty )\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() is a solution of (1.5) with $y(s)= \Lambda (s,\,s) \xi = \xi$
is a solution of (1.5) with $y(s)= \Lambda (s,\,s) \xi = \xi$![]() such that $\Lambda$
such that $\Lambda$![]() is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() , then
, then

Proof. It is easy to see from (2.6) that

and

for each $(t,\,s)\in I^{2}_{\geq }$![]() . Equality (3.12) can be rewritten in the equivalent form
. Equality (3.12) can be rewritten in the equivalent form

For convenience we can assume that $D=\|\Lambda \|_{c}<\infty$![]() , since $\Lambda$
, since $\Lambda$![]() is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Then it follows from (2.5) and (1.4) that
. Then it follows from (2.5) and (1.4) that
Since $\alpha >\varepsilon$![]() , the right-hand side of this inequality goes to zero as $t\rightarrow +\infty$
, the right-hand side of this inequality goes to zero as $t\rightarrow +\infty$![]() . Furthermore, we have
. Furthermore, we have

and

Taking limits as $t\rightarrow +\infty$![]() in (3.13), we obtain
in (3.13), we obtain

and substituting it into (3.12) yields

Since $\xi$![]() is an arbitrary one in ${\Bbb R}^{n}$
is an arbitrary one in ${\Bbb R}^{n}$![]() , then by adding this identity to (3.11) yields the desired equation (3.10).
, then by adding this identity to (3.11) yields the desired equation (3.10).
Recall that $\hat {\Phi }(t,\,s)=\hat {\Phi }(t)\hat {\Phi }^{-1}(s)$![]() denotes the fundamental matrix solution of (1.5) with $\hat {\Phi }(s,\,s)=Id$
denotes the fundamental matrix solution of (1.5) with $\hat {\Phi }(s,\,s)=Id$![]() . For each $t\in I$
. For each $t\in I$![]() , define linear operators as
, define linear operators as
where $t_{0}$![]() is the left boundary point of the interval $I$
is the left boundary point of the interval $I$![]() . After presenting that $\hat {P}(t)$
. After presenting that $\hat {P}(t)$![]() are projections, we prove relationship (3.2), show the explicit expressions of the fundamental matrix solution $\hat {\Phi }(t,\,s)$
are projections, we prove relationship (3.2), show the explicit expressions of the fundamental matrix solution $\hat {\Phi }(t,\,s)$![]() under the projections $\hat {P}(t)$
under the projections $\hat {P}(t)$![]() , $\hat {Q}(t)$
, $\hat {Q}(t)$![]() , and then deduce inequalities (3.3) and (3.4).
, and then deduce inequalities (3.3) and (3.4).
Lemma 3.5 The operator $\hat {P}(t)$![]() is a linear projection for $t\in I$
is a linear projection for $t\in I$![]() , and (3.2) holds.
, and (3.2) holds.
Proof. By lemma 3.3, we have $U(t_{0},\,t_{0})U(t_{0},\,t_{0})=U(t_{0},\,t_{0})$![]() . Thus,
. Thus,
Furthermore, for any $t,\, s\in I$![]() , we obtain
, we obtain

and this completes the proof of the lemma.
Lemma 3.6 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $\hat {P}(t)\hat {\Phi }(t,\,s)$
is a solution of (1.5) with $\hat {P}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() .
.
Proof. By lemma 3.2, the function $U(t,\,t_{0})\xi _{0}$![]() is a solution of (1.5) with initial value $U(t_{0},\,t_{0})\xi _{0}$
is a solution of (1.5) with initial value $U(t_{0},\,t_{0})\xi _{0}$![]() at time $t_{0}$
at time $t_{0}$![]() . Clearly, $U(t,\,t_{0})=\hat {\Phi }(t,\,t_{0})U(t_{0},\,t_{0})$
. Clearly, $U(t,\,t_{0})=\hat {\Phi }(t,\,t_{0})U(t_{0},\,t_{0})$![]() . Thus, it is easy to see that
. Thus, it is easy to see that
Therefore, it follows again from lemma 3.2 that $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}=U(t,\,t_{0})\hat {\Phi }(t_{0},\,s)\xi _{0}$![]() is a solution of (1.5) with initial value $\hat {\Phi }(t_{0},\,s)\xi _{0} \!\in\! {\Bbb R}^{n}$
is a solution of (1.5) with initial value $\hat {\Phi }(t_{0},\,s)\xi _{0} \!\in\! {\Bbb R}^{n}$![]() . Moreover, from $U \!\in\! (\mathscr {L}_{c},\, \|\cdot \|_{c})$
. Moreover, from $U \!\in\! (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() and definition (2.4)–(2.5) of the space $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
and definition (2.4)–(2.5) of the space $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() , we can see that $\hat {P}(t)\hat {\Phi }(t,\,s)$
, we can see that $\hat {P}(t)\hat {\Phi }(t,\,s)$![]() is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() .
.
Lemma 3.7 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in I^{2}_{\geq }$
is a solution of (1.5) with $(t,\,s)\in I^{2}_{\geq }$![]() such that
such that

Proof. Let $y(t)=\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() with given $s\in I$
with given $s\in I$![]() , and denote $\xi =\hat {P}(s)\xi _{0}$
, and denote $\xi =\hat {P}(s)\xi _{0}$![]() the initial condition at time $s$
the initial condition at time $s$![]() . Clearly, $y(t)$
. Clearly, $y(t)$![]() is a solution of (1.5) with $y(s)=\hat {P}(s)\xi _{0}=\hat {P}(s)\hat {P}(s)\xi _{0}=\xi$
is a solution of (1.5) with $y(s)=\hat {P}(s)\xi _{0}=\hat {P}(s)\hat {P}(s)\xi _{0}=\xi$![]() . By lemma 3.6, $\hat {P}(t)\hat {\Phi }(t,\,s)$
. By lemma 3.6, $\hat {P}(t)\hat {\Phi }(t,\,s)$![]() is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Since $\xi _{0}$
. Since $\xi _{0}$![]() is arbitrary in ${\Bbb R}^{n}$
is arbitrary in ${\Bbb R}^{n}$![]() , identity (3.15) follows now readily from lemma 3.4.
, identity (3.15) follows now readily from lemma 3.4.
Remark 3.8 From lemma 3.7, we know that the explicit expressions (2.6) and (3.5) are the same under the condition of NMS-EC. In fact, as a special case of lemma 3.7, $\hat {\Phi }(t,\,s)$![]() is always bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
is always bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() with $I=[t_{0},\,+\infty )$
with $I=[t_{0},\,+\infty )$![]() since projections are the identity.
since projections are the identity.
In the following lemma, we present the explicit expression of $\hat {\Phi }(t,\,s)\hat {Q}(s)$![]() with $(t,\,s)\in I^{2}_{\leq }$
with $(t,\,s)\in I^{2}_{\leq }$![]() .
.
Lemma 3.9 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in I^{2}_{\leq }$
is a solution of (1.5) with $(t,\,s)\in I^{2}_{\leq }$![]() such that
such that

Proof. Following the same lines as given in the proof of lemma 2.2, one can prove that

for any $(t,\,s) \in I^{2}_{\leq }$![]() . Write $K(t)=\hat {\Phi }(t,\,t_{0})\hat {Q}(t_{0})$
. Write $K(t)=\hat {\Phi }(t,\,t_{0})\hat {Q}(t_{0})$![]() . Therefore,
. Therefore,

On the other hand, it follows from $\hat {P}(t)=\hat {\Phi }(t,\,t_{0})U(t_{0},\,t_{0})\hat {\Phi }(t_{0},\,t)$![]() and (3.5) with $t=s=t_{0}$
and (3.5) with $t=s=t_{0}$![]() that
that

Since $P(t_{0})$![]() and $Q(t_{0})$
and $Q(t_{0})$![]() are complementary projections, multiplying (3.18) on the left with $P(t_{0})$
are complementary projections, multiplying (3.18) on the left with $P(t_{0})$![]() gives
gives
In addition,
By (3.17), using (3.20), we have

which can be rewritten as

Substituting (3.21) into (3.17) leads to

Since (3.2) we have $K(t)=\hat {\Phi }(t,\,t_{0})\hat {Q}(t_{0})=\hat {Q}(t)\hat {\Phi }(t,\,t_{0})$![]() . Therefore, $K(t)\hat {\Phi }(t_{0},\,s)=\hat {Q}(t)\hat {\Phi }(t,\,s)$
. Therefore, $K(t)\hat {\Phi }(t_{0},\,s)=\hat {Q}(t)\hat {\Phi }(t,\,s)$![]() for every $(t,\,s) \in I^{2}_{\le }$
for every $(t,\,s) \in I^{2}_{\le }$![]() . Thus, multiplying (3.22) on the right with $\hat {\Phi }(t_{0},\,s)$
. Thus, multiplying (3.22) on the right with $\hat {\Phi }(t_{0},\,s)$![]() yields the desired identity (3.16).
yields the desired identity (3.16).
We proceed with the proof of theorem 3.1. Squaring both sides of (3.15), and taking expectations. Setting $z(t,\,s)={\mathbb {E}}\|\hat {\Phi }(t,\,s)\hat {P}(s)\|^{2}$![]() with $(t,\,s) \in I^{2}_{\ge }$
with $(t,\,s) \in I^{2}_{\ge }$![]() . It follows from (2.7) that
. It follows from (2.7) that

By using the Itô isometry property and inequalities (1.3), the second term on the right-hand side of (3.23) can be deduced as follows:

As to the third term in (3.23), it follows from ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$![]() , Cauchy–Schwarz inequality and inequalities (1.3) that
, Cauchy–Schwarz inequality and inequalities (1.3) that

Clearly, the proof above is also valid for proving the other terms on the right-hand side in (3.23). Thus, we can rewrite inequality (3.23) as

with $\tilde {M}=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() . Let
. Let

Clearly, inequality (3.24) can be rewritten as
On the contrary,
and therefore,

Integrating the above inequality from $s$![]() to $t$
to $t$![]() and note that $Z(s,\,s)=5Me^{\varepsilon |s|}z(s,\,s)$
and note that $Z(s,\,s)=5Me^{\varepsilon |s|}z(s,\,s)$![]() , we obtain
, we obtain
By $z(t,\,s)={\mathbb {E}}\|\hat {\Phi }(t,\,s)\hat {P}(s)\|^{2}$![]() , we have
, we have
Similarly, squaring both sides of (3.16), and taking expectations. Using the same way as above, we obtain
Now we try to find out the bounds in mean-square setting for the projections $\hat {P}(t)$![]() , $\hat {Q}(t)$
, $\hat {Q}(t)$![]() . Multiplying (3.15) with $Q(t)$
. Multiplying (3.15) with $Q(t)$![]() on the left side, and let $t=s$
on the left side, and let $t=s$![]() , we have
, we have

By (3.27), using (1.4), (3.1) and (3.25), we have

since $\alpha >\varepsilon$![]() and $\tilde {\alpha }=\frac {\alpha }{2}-{10M\tilde {M}}/{\alpha }>0$
and $\tilde {\alpha }=\frac {\alpha }{2}-{10M\tilde {M}}/{\alpha }>0$![]() . In addition, it follows from (3.16) with $t=s$
. In addition, it follows from (3.16) with $t=s$![]() that
that

Similarly, by (3.29), using (1.3), (3.1) and (3.26), we obtain
Meanwhile, notice that

Thus it follows from (3.28) and (3.30) that
Furthermore, it follows from (1.3)–(1.4) with $t=s$![]() that
that
Therefore,

Since $\hat {Q}(t)-Q(t)=(Id-\hat {P}(t))-(Id-P(t))=P(t)-\hat {P}(t)$![]() , we also have
, we also have

Then we know
and hence,

Since $\tilde {M}:=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() , we can obtain
, we can obtain
by letting $b$![]() and $h$
and $h$![]() sufficiently small. This yields
sufficiently small. This yields
By (3.25), (3.26), using (3.32) we obtain
and
This completes the proof of the theorem.
Under the hypotheses of theorem 3.1, the following theorem tries to discuss the differences of projections $P(t)$![]() and $\hat {P}(t)$
and $\hat {P}(t)$![]() in the mean-square sense. To illustrate it clearly, write
in the mean-square sense. To illustrate it clearly, write
Obviously, $\Phi (t,\,s)$![]() is a fundamental matrix solution of (1.1) with $\Phi (s,\,s)=Id$
is a fundamental matrix solution of (1.1) with $\Phi (s,\,s)=Id$![]() .
.
Theorem 3.10 Under the hypotheses of theorem 3.1, for any $t\in I$![]() , we have
, we have
and
In particular, for each fixed $t\in I$![]() , we have ${\mathbb {E}}\|P(t)-\hat {P}(t)\|^{2}\rightarrow 0$
, we have ${\mathbb {E}}\|P(t)-\hat {P}(t)\|^{2}\rightarrow 0$![]() as $b,\, h \rightarrow 0$
as $b,\, h \rightarrow 0$![]() .
.
Proof. The second equality of (3.33) is obvious from definition (3.14) of linear operators $\hat {P}(t)$![]() . For the first term in (3.33), it follows from (1.2) that
. For the first term in (3.33), it follows from (1.2) that
and then
Taking $s=t_{0}$![]() in (3.35), we obtain
in (3.35), we obtain
Thus,
In addition, (3.34) follows immediately from (3.31) and (3.32).
Theorem 3.11 Under the hypotheses of theorem 3.1, we have
and
Proof. By $\hat {P}(s)\hat {P}(s)=\hat {P}(s)$![]() , it follows from (3.15) that
, it follows from (3.15) that

By (1.3) and (3.3), using $\alpha -\hat {\alpha }=\frac {\alpha }{2}+\frac {10M\tilde {M}}{\alpha }>0$![]() , the first term on the right-hand side in (3.36) can be deduced as follows:
, the first term on the right-hand side in (3.36) can be deduced as follows:

As to the second term in (3.36), by $\frac {\alpha }{2}-\hat {\alpha }=\frac {10M\tilde {M}}{\alpha }>0$![]() , we have $2\alpha ^{2}-\alpha \hat {\alpha }>0$
, we have $2\alpha ^{2}-\alpha \hat {\alpha }>0$![]() . It follows from ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$
. It follows from ${\mathbb {E}}\|x\|\le \sqrt {{\mathbb {E}}\|x\|^{2}}$![]() , Cauchy–Schwarz inequality and inequalities (1.3), (3.3) that
, Cauchy–Schwarz inequality and inequalities (1.3), (3.3) that

Clearly, the proof above is also valid for proving the other terms on the right-hand side in (3.36). Thus, we can rewrite inequality (3.36) as

Additionally, as $\hat {P}(s)$![]() and $\hat {Q}(s)$
and $\hat {Q}(s)$![]() are complementary projections for each $s\in I$
are complementary projections for each $s\in I$![]() , it follows from(1.3), (3.4) and (3.29) that
, it follows from(1.3), (3.4) and (3.29) that

Combining (3.37) and (3.38) yields

Similarly, by (3.16) we obtain
Also, as $\hat {P}(s)$![]() and $\hat {Q}(s)$
and $\hat {Q}(s)$![]() are complementary projections for each $s\in I$
are complementary projections for each $s\in I$![]() , by (3.28) we obtain
, by (3.28) we obtain
Combining (3.39) and (3.40) yields

This completes the proof of the theorem.
Remark 3.12 Since $I=[t_{0},\,+\infty )$![]() , the second-moment Lyapunov exponent is bounded by $-\hat {\alpha }$
, the second-moment Lyapunov exponent is bounded by $-\hat {\alpha }$![]() for any fixed $b,\, h >0$
for any fixed $b,\, h >0$![]() , i.e.
, i.e.
This shows that in the stable direction, any two solutions $\hat {\Phi }(t,\,s)\hat {P}(s)\xi$![]() and $\Phi (t,\,s)P(s)\xi$
and $\Phi (t,\,s)P(s)\xi$![]() with the same initial condition are forward asymptotic in the mean-square sense. Furthermore, since $M=8b^{2}+8g^{2}h^{2}+\alpha h^2$
with the same initial condition are forward asymptotic in the mean-square sense. Furthermore, since $M=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() , for each fixed $T_{1}\in (s,\,+\infty )$
, for each fixed $T_{1}\in (s,\,+\infty )$![]() and $T_{2} \in (t_{0},\,s)$
and $T_{2} \in (t_{0},\,s)$![]() , we have
, we have
and
This means that the solution $\hat {\Phi }(t,\,s)\hat {P}(s)$![]() (or $\hat {\Phi }(t,\,s)\hat {Q}(s)$
(or $\hat {\Phi }(t,\,s)\hat {Q}(s)$![]() ) of the perturbed system (1.5) approaches uniformly the solution $\Phi (t,\,s)P(s)$
) of the perturbed system (1.5) approaches uniformly the solution $\Phi (t,\,s)P(s)$![]() (or $\Phi (t,\,s)Q(s)$
(or $\Phi (t,\,s)Q(s)$![]() ) of system (1.1) in the mean-square sense on any compact interval.
) of system (1.1) in the mean-square sense on any compact interval.
4. Robustness of NMS-ED on the half line $(-\infty,\,t_{0}]$
In this section, we deal with the robustness of NMS-ED on $I= (-\infty,\,t_{0}]$![]() , which is analogous to the case $[t_{0},\,+\infty )$
, which is analogous to the case $[t_{0},\,+\infty )$![]() . So in what follows, we highlight the main steps of the proof which only indicate the major differences.
. So in what follows, we highlight the main steps of the proof which only indicate the major differences.
Theorem 4.1 The assertion in theorem 3.1 remains true for $I= (-\infty,\,t_{0}]$![]() .
.
Proof of theorem 4.1. Proof of theorem 4.1
Consider the Banach space
with the norm
Following the same steps as in the proof of theorem 1, we establish the following statements.
Lemma 4.2 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , (1.5) has a unique solution $V(t,\,s) \xi _{0}$
, (1.5) has a unique solution $V(t,\,s) \xi _{0}$![]() with $V \in (\mathscr {L}_{d},\, \|\cdot \|_{d})$
with $V \in (\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() such that
such that

Lemma 4.3 For any $u\in (t,\,s)$![]() in $I$
in $I$![]() , we have
, we have
in the sense of $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() .
.
Lemma 4.4 Given $s\in I$![]() , if $y(t):=\tilde {\Lambda }(t,\,s) \xi :(-\infty,\,s]\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
, if $y(t):=\tilde {\Lambda }(t,\,s) \xi :(-\infty,\,s]\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() is a solution of (1.5) with $y(s)= \tilde {\Lambda }(s,\,s) \xi = \xi$
is a solution of (1.5) with $y(s)= \tilde {\Lambda }(s,\,s) \xi = \xi$![]() such that $\tilde {\Lambda }$
such that $\tilde {\Lambda }$![]() is bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$
is bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() . Then
. Then

For each $t\in I$![]() , define linear operators as
, define linear operators as
where $t_{0}$![]() is the right boundary point of the interval $I$
is the right boundary point of the interval $I$![]() .
.
Lemma 4.5 The operator $\hat {P}(t)$![]() is a linear projection for $t\in I$
is a linear projection for $t\in I$![]() , and (3.2) holds.
, and (3.2) holds.
Lemma 4.6 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $\hat {Q}(t)\hat {\Phi }(t,\,s)$
is a solution of (1.5) with $\hat {Q}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$
bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() .
.
Lemma 4.7 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in I^{2}_{\leq }$
is a solution of (1.5) with $(t,\,s)\in I^{2}_{\leq }$![]() such that
such that

Lemma 4.8 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\hat {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in I^{2}_{\geq }$
is a solution of (1.5) with $(t,\,s)\in I^{2}_{\geq }$![]() such that
such that

Proceeding as in the proof of theorem 3.1. Squaring both sides of (4.5), and taking expectations, we obtain
Similarly, squaring both sides of (4.6), and taking expectations, we obtain
Meanwhile, multiplying (4.5) with $P(t)$![]() and (4.6) with $Q(t)$
and (4.6) with $Q(t)$![]() on the left side, respectively, and let $t=s$
on the left side, respectively, and let $t=s$![]() , we obtain
, we obtain
and
Since
and $\hat {P}(t)-P(t)=Q(t)\hat {P}(t)-P(t)\hat {Q}(t)$![]() , for sufficiently small $b$
, for sufficiently small $b$![]() and $h$
and $h$![]() , we obtain the bounds for the projections $\hat {P}(t)$
, we obtain the bounds for the projections $\hat {P}(t)$![]() and $\hat {Q}(t)$
and $\hat {Q}(t)$![]() as follows:
as follows:
By (4.7), (4.8), using (4.9) we obtain
and
This completes the proof of the theorem.
5. Robustness of NMS-ED on the whole ${\Bbb R}$
In this section, we consider the robustness of NMS-ED on the whole $I= {\Bbb R}$![]() . From the last two sections we know that if (3.1) holds, the perturbed equation (1.5) remains NMS-ED on $[t_{0},\,+\infty )$
. From the last two sections we know that if (3.1) holds, the perturbed equation (1.5) remains NMS-ED on $[t_{0},\,+\infty )$![]() with the operators:
with the operators:
and on $(-\infty,\, t_{0}]$![]() with the operators:
with the operators:
The most important part in this section is to show that (1.5) has an NMS-ED on both half lines with the same projections. For this purpose, we introduce modified projections, which combine the advantages of projections $\hat {P}_+(t)$![]() and $\hat {Q}_{-}(t)$
and $\hat {Q}_{-}(t)$![]() . Actually, this technique has been used in several papers to deal with this problem, see e.g. [Reference Barreira, Silva and Valls5, Reference Barreira and Valls7, Reference Palmer39, Reference Palmer40, Reference Popescu44, Reference Popescu45] for details.
. Actually, this technique has been used in several papers to deal with this problem, see e.g. [Reference Barreira, Silva and Valls5, Reference Barreira and Valls7, Reference Palmer39, Reference Palmer40, Reference Popescu44, Reference Popescu45] for details.
In the following, for convenience and brevity, let us denote by $G(t,\,s)$![]() the Green function of (1.1):
the Green function of (1.1):
Green function is a classical concept in the study of exponential dichotomy as for example [Reference Chicone and Latushkin8, Reference Engel and Nagel15]. Now we deal with the robustness of NMS-ED for (1.1) on the whole ${\Bbb R}$![]() .
.
Theorem 5.1 The assertion in theorem 3.1 remains true for $I= {\Bbb R}$![]() .
.
Proof of theorem 5.1. Proof of theorem 5.1
Consider the Banach spaces
and
with the norm
and
respectively. Define operator $\Gamma _{1}:\mathscr {L}_{c} \rightarrow \mathscr {L}_{c}$![]() by
by

and operator $\Gamma _{2}:\mathscr {L}_{d} \rightarrow \mathscr {L}_{d}$![]() ,
,

Similar arguments to those in the proofs of lemma 3.2 and lemma 4.2 can be used to deduce that
with $\theta =\sqrt {\frac {10M\tilde {M}}{\alpha ^{2}} }<1$![]() . Thus, we have the following lemma.
. Thus, we have the following lemma.
Lemma 5.2 Operators $\Gamma _{1}$![]() , $\Gamma _{2}$
, $\Gamma _{2}$![]() have unique fixed points $U\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$
have unique fixed points $U\in (\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() , respectively $V\in (\mathscr {L}_{d},\, \|\cdot \|_{d})$
, respectively $V\in (\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() such that
such that

and

Repeating arguments in the proofs of theorems 3.1 and 4.1, we obtain the following statements.
Lemma 5.3 For any $u\in (s,\,t)$![]() in $I$
in $I$![]() , we have
, we have
in the sense of $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() , respectively,
, respectively,
in the sense of $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() .
.
Lemma 5.4 Given $s\in I$![]() , if $x(t)=\Lambda (t,\,s) \xi :[s,\,+\infty )\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
, if $x(t)=\Lambda (t,\,s) \xi :[s,\,+\infty )\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() (respectively, $y(t):=\tilde {\Lambda }(t,\,s) \xi :(-\infty,\,s]\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$
(respectively, $y(t):=\tilde {\Lambda }(t,\,s) \xi :(-\infty,\,s]\rightarrow L^{2}(\Omega,\, {\Bbb R}^{n})$![]() ) is a solution of (1.5) with $x(s)= \Lambda (s,\,s) \xi = \xi$
) is a solution of (1.5) with $x(s)= \Lambda (s,\,s) \xi = \xi$![]() (respectively, $y(s)= \tilde {\Lambda }(s,\,s) \xi = \xi$
(respectively, $y(s)= \tilde {\Lambda }(s,\,s) \xi = \xi$![]() ) such that $\Lambda$
) such that $\Lambda$![]() (respectively, $\tilde {\Lambda }$
(respectively, $\tilde {\Lambda }$![]() ) is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
) is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() (respectively, $(\mathscr {L}_{d},\, \|\cdot \|_{d})$
(respectively, $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() ), then
), then

and

Now we present that projection $S=\hat {P}_+(t_{0})+\hat {Q}_{-}(t_{0})$![]() is invertible for some $t_{0}\in {\Bbb R}$
is invertible for some $t_{0}\in {\Bbb R}$![]() with $b$
with $b$![]() and $h$
and $h$![]() sufficiently small. Using this result, we are able to define modified operators.
sufficiently small. Using this result, we are able to define modified operators.
Lemma 5.5 If $b$![]() and $h$
and $h$![]() are sufficiently small, then the operator $S=\hat {P}_+(t_{0})+\hat {Q}_{-}(t_{0})$
are sufficiently small, then the operator $S=\hat {P}_+(t_{0})+\hat {Q}_{-}(t_{0})$![]() is invertible.
is invertible.
Proof. We first derive $\hat {P}_+(t_{0})P(t_{0})=\hat {P}_+(t_{0})$![]() . In fact, following the same procedure as we did for lemma 3.3, we find that
. In fact, following the same procedure as we did for lemma 3.3, we find that
Since $\hat {P}_+(t_{0})=U(t_{0},\,t_{0})$![]() , by (5.3) with $t=s=t_{0}$
, by (5.3) with $t=s=t_{0}$![]() we have
we have
In addition, we have (see (3.19))
Since $\hat {Q}_{-}(t_{0})=V(t_{0},\,t_{0})$![]() , a similar argument using lemma 4.3 with $t=s=t_{0}$
, a similar argument using lemma 4.3 with $t=s=t_{0}$![]() yields
yields
Furthermore, it follows from $\hat {Q}_{-}(t)=\hat {\Phi }(t,\,t_{0})V(t_{0},\,t_{0})\hat {\Phi }(t_{0},\,t)$![]() and (4.3) with $t=s=t_{0}$
and (4.3) with $t=s=t_{0}$![]() that
that

Since $P(t_{0})$![]() and $Q(t_{0})$
and $Q(t_{0})$![]() are complementary projections, multiplying (5.7) on the left with $Q(t_{0})$
are complementary projections, multiplying (5.7) on the left with $Q(t_{0})$![]() gives
gives
We now consider the linear operators
It follows easily from (5.4) and (5.5) that $S_{1}T_{1}=T_{1}S_{1}=Id$![]() . Therefore, $S_{1}$
. Therefore, $S_{1}$![]() is invertible and $S_{1}^{-1}=T_{1}$
is invertible and $S_{1}^{-1}=T_{1}$![]() . In addition, using again (5.5) we obtain
. In addition, using again (5.5) we obtain

By (3.18), we have

To estimate the bounds of the integral in the mean-square sense, we need to find out the bounds for $U(t,\, t_{0})$![]() with $t\ge t_{0}$
with $t\ge t_{0}$![]() . Squaring both sides of (3.5), taking expectations and proceeding as in the proof of theorem 3.1, for any $t\ge t_{0}$
. Squaring both sides of (3.5), taking expectations and proceeding as in the proof of theorem 3.1, for any $t\ge t_{0}$![]() , we have
, we have

By (5.10), using (5.11) and (5.12), we obtain

Meanwhile, we consider the linear operators
It follows easily from (5.6) and (5.8) that $S_{2}T_{2}=T_{2}S_{2}=Id$![]() . Therefore, $S_{2}$
. Therefore, $S_{2}$![]() is invertible and $S_{2}^{-1}=T_{2}$
is invertible and $S_{2}^{-1}=T_{2}$![]() . In addition, using again (5.8) we obtain
. In addition, using again (5.8) we obtain

By (5.7),

Similarly, for any $t\le t_{0}$![]() , one can deduce from (4.3) that
, one can deduce from (4.3) that

Therefore, by (5.15), using (5.16) and (5.17) we obtain
Besides, it follows easily from (5.8) that $P(t_{0})\hat {P}_{-}(t_{0})=\hat {P}_{-}(t_{0})$![]() . Using also (5.5) yields
. Using also (5.5) yields

By (5.13) and (5.18) we obtain

Moreover,

Since $\tilde {M}:=8b^{2}+8g^{2}h^{2}+\alpha h^2$![]() , by (5.13), respectively, (5.18), we can make invertible operators $S_{1}$
, by (5.13), respectively, (5.18), we can make invertible operators $S_{1}$![]() and $S_{2}$
and $S_{2}$![]() such that ${\mathbb {E}}\|S_{1}-Id\|^{2}$
such that ${\mathbb {E}}\|S_{1}-Id\|^{2}$![]() and ${\mathbb {E}}\|S_{2}-Id\|^{2}$
and ${\mathbb {E}}\|S_{2}-Id\|^{2}$![]() as small as desired with $b$
as small as desired with $b$![]() and $h$
and $h$![]() sufficiently small. So if taking $b$
sufficiently small. So if taking $b$![]() and $h$
and $h$![]() sufficiently small, it follows from (5.19) and (5.20) that $S=\hat {P}_+(t_{0})+\hat {Q}_{-}(t_{0})$
sufficiently small, it follows from (5.19) and (5.20) that $S=\hat {P}_+(t_{0})+\hat {Q}_{-}(t_{0})$![]() is invertible.
is invertible.
For each $t\in I$![]() , define linear operators as
, define linear operators as
Lemma 5.6 The operator $\tilde {P}(t)$![]() is a linear projection for $t\in I$
is a linear projection for $t\in I$![]() , and (3.2) holds for any $t,\, s\in {\Bbb R}$
, and (3.2) holds for any $t,\, s\in {\Bbb R}$![]() .
.
Proof. Obviously,
Moreover, for any $t,\, s\in {\Bbb R}$![]() , we obtain
, we obtain

and this completes the proof of the lemma.
Lemma 5.7 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $\tilde {P}(t)\hat {\Phi }(t,\,s)$
is a solution of (1.5) with $\tilde {P}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() , respectively, the function $\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, respectively, the function $\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $\tilde {Q}(t)\hat {\Phi }(t,\,s)$
is a solution of (1.5) with $\tilde {Q}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$
bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() .
.
Proof. In view of (5.4) and (5.6), we have

Thus,

Therefore, it follows from lemma 3.6 that $\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}=\hat {\Phi }(t,\,t_{0})\hat {P}_+(t_{0})S^{-1} \hat {\Phi}(t_{0},\,s)\xi _{0}$![]() is a solution of (1.5) with initial value $S^{-1} \hat {\Phi }(t_{0},\,s)\xi _{0} \in {\Bbb R}^{n}$
is a solution of (1.5) with initial value $S^{-1} \hat {\Phi }(t_{0},\,s)\xi _{0} \in {\Bbb R}^{n}$![]() with $\tilde {P}(t)\hat {\Phi }(t,\,s)$
with $\tilde {P}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() . Similarly, by lemma 4.6, we have $\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
. Similarly, by lemma 4.6, we have $\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() as a solution of (1.5) with initial value $S^{-1} \hat {\Phi }(t_{0},\,s)\xi _{0} \in {\Bbb R}^{n}$
as a solution of (1.5) with initial value $S^{-1} \hat {\Phi }(t_{0},\,s)\xi _{0} \in {\Bbb R}^{n}$![]() with $\tilde {Q}(t)\hat {\Phi }(t,\,s)$
with $\tilde {Q}(t)\hat {\Phi }(t,\,s)$![]() bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$
bounded in $(\mathscr {L}_{d},\, \|\cdot \|_{d})$![]() .
.
Lemma 5.8 For any given initial value $\xi _{0} \in {\Bbb R}^{n}$![]() , the function $\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$
, the function $\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in {\Bbb R}^{2}_{\geq }$
is a solution of (1.5) with $(t,\,s)\in {\Bbb R}^{2}_{\geq }$![]() such that
such that

and the function $\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() is a solution of (1.5) with $(t,\,s)\in {\Bbb R}^{2}_{\leq }$
is a solution of (1.5) with $(t,\,s)\in {\Bbb R}^{2}_{\leq }$![]() such that
such that

Proof. Let $x(t)=\tilde {P}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() (respectively, $y(t)=\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$
(respectively, $y(t)=\tilde {Q}(t)\hat {\Phi }(t,\,s)\xi _{0}$![]() ) with given $s\in {\Bbb R}$
) with given $s\in {\Bbb R}$![]() , and denote $\xi =\tilde {P}(s)\xi _{0}$
, and denote $\xi =\tilde {P}(s)\xi _{0}$![]() the initial condition at time $s$
the initial condition at time $s$![]() . Clearly, $x(t)$
. Clearly, $x(t)$![]() (respectively, $y(t)$
(respectively, $y(t)$![]() ) is a solution of (1.5) with $x(s)=\tilde {P}(s)\xi =\tilde {P}(s)\tilde {P}(s)\xi _{0}=\xi$
) is a solution of (1.5) with $x(s)=\tilde {P}(s)\xi =\tilde {P}(s)\tilde {P}(s)\xi _{0}=\xi$![]() (respectively, $y(s)=\tilde {Q}(s)\xi =\tilde {Q}(s)\tilde {Q}(s)\xi _{0}=\xi$
(respectively, $y(s)=\tilde {Q}(s)\xi =\tilde {Q}(s)\tilde {Q}(s)\xi _{0}=\xi$![]() ). By lemma 5.7, $\tilde {P}(t)\hat {\Phi }(t,\,s)$
). By lemma 5.7, $\tilde {P}(t)\hat {\Phi }(t,\,s)$![]() (respectively, $\tilde {Q}(t)\hat {\Phi }(t,\,s)$
(respectively, $\tilde {Q}(t)\hat {\Phi }(t,\,s)$![]() ) is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$
) is bounded in $(\mathscr {L}_{c},\, \|\cdot \|_{c})$![]() (respectively, $(\mathscr {L}_{d},\, \|\cdot \|_{d}))$
(respectively, $(\mathscr {L}_{d},\, \|\cdot \|_{d}))$![]() . Since $\xi _{0}$
. Since $\xi _{0}$![]() is arbitrary in ${\Bbb R}^{n}$
is arbitrary in ${\Bbb R}^{n}$![]() , identity (5.22) (respectively, (5.23)) follows now readily from (5.1) (respectively, (5.2)).
, identity (5.22) (respectively, (5.23)) follows now readily from (5.1) (respectively, (5.2)).
Proceed as in the proof of theorem 3.1. Squaring both sides of (5.22), and taking expectations, we obtain
Similarly, squaring both sides of (5.23), and taking expectations, we obtain
Meanwhile, multiplying (5.22) with $Q(t)$![]() and (5.23) with $P(t)$
and (5.23) with $P(t)$![]() on the left side, respectively, and let $t=s$
on the left side, respectively, and let $t=s$![]() , we obtain
, we obtain
and
Since
and $\tilde {P}(t)-P(t)=Q(t)\tilde {P}(t)-P(t)\tilde {Q}(t)$![]() , for sufficiently small $b$
, for sufficiently small $b$![]() and $h$
and $h$![]() , we obtain the bounds for the projections $\tilde {P}(t)$
, we obtain the bounds for the projections $\tilde {P}(t)$![]() and $\tilde {Q}(t)$
and $\tilde {Q}(t)$![]() as follows:
as follows:
By (5.24), (5.25), using (5.26) we obtain
and
This completes the proof of the theorem.
Remark 5.9 By (5.9), using (5.4) and (5.5), we obtain

Thus, it follows from (3.14) that
Meanwhile, by (5.14), using (5.6) and (5.8), we obtain

Thus it follows from (4.4) that
and consequently,
By (5.21), (5.27) and (5.28), we know that linear operators $\hat {P}_+(t)$![]() , $\hat {P}_{-}(t)$
, $\hat {P}_{-}(t)$![]() and $\tilde {P}(t)$
and $\tilde {P}(t)$![]() , defined on $[t_{0},\,+\infty )$
, defined on $[t_{0},\,+\infty )$![]() , $(-\infty,\,t_{0}]$
, $(-\infty,\,t_{0}]$![]() and ${\Bbb R}$
and ${\Bbb R}$![]() respectively, are actually obtained under the same rules.
respectively, are actually obtained under the same rules.
Remark 5.10 Throughout this paper, we choose any fixed $t_{0} \in {\Bbb R}$![]() instead of $0\in {\Bbb R}$
instead of $0\in {\Bbb R}$![]() , which is a little different from the one given in uniform exponential dichotomy (see e.g. [Reference Popescu44]), where the initial point $0$
, which is a little different from the one given in uniform exponential dichotomy (see e.g. [Reference Popescu44]), where the initial point $0$![]() is used for simplicity, and there is no substantial difference in inequalities thus obtained. However, here we have to choose general term $t_{0}$
is used for simplicity, and there is no substantial difference in inequalities thus obtained. However, here we have to choose general term $t_{0}$![]() instead of $0$
instead of $0$![]() since the nonuniform item will vanish at time $0$
since the nonuniform item will vanish at time $0$![]() , and hence there is a significant difference in some calculations.
, and hence there is a significant difference in some calculations.
6. Example
In what follows we use an example to demonstrate our results. The following example shows that there exists a linear SDE which admits an NMS-ED but not uniform.
Example 6.1 Let $a>b>0$![]() be real parameters. Then the following linear SDE:
be real parameters. Then the following linear SDE:
with the initial condition $u(0)=v(0)=1$![]() admits an NMS-ED that is not a uniform MS-ED.
admits an NMS-ED that is not a uniform MS-ED.
Proof. Let
be a fundamental matrix solution of (6.1). Thus we have $u(t)=U(t)U^{-1}(s)u(s)$![]() and $v(t)=V(t)V^{-1}(s)v(s)$
and $v(t)=V(t)V^{-1}(s)v(s)$![]() . In addition, it is easy to verify that
. In addition, it is easy to verify that
is a fundamental matrix solution of
Hence, by [Reference Evans16, p. 97], the solution of (6.1) is given by

since $u(0)=v(0)=1$![]() . Therefore,
. Therefore,

Thus, one can obtain
since ${\mathbb {E}}\|u(s)\|^{2}>0$![]() . It is easy to see that
. It is easy to see that
and thus
Furthermore, if $t =4k\pi$![]() and $s =3k\pi$
and $s =3k\pi$![]() with $k\in {\Bbb N}$
with $k\in {\Bbb N}$![]() , then
, then
Similarly, one can prove that
and
if $t =4k\pi$![]() and $s =3k\pi$
and $s =3k\pi$![]() with $k\in {\Bbb N}$
with $k\in {\Bbb N}$![]() . Thus, (6.1) admits an NMS-ED. By (6.3) and/or (6.5), the exponential $e^{2b s}$
. Thus, (6.1) admits an NMS-ED. By (6.3) and/or (6.5), the exponential $e^{2b s}$![]() in (6.2) and/or (6.4) cannot be removed. This shows that the NMS-ED is not uniform.
in (6.2) and/or (6.4) cannot be removed. This shows that the NMS-ED is not uniform.
Remark 6.2 The SDE (6.1) in example 6.1 admitting an NMS-ED is linear in the narrow sense. Following the same idea and method in [Reference Zhu and Chen60], one can establish a general linear SDE, which admits an NMS-ED. For example, let $a>b>0$![]() be real parameters, one can prove the following linear SDE
be real parameters, one can prove the following linear SDE
with the initial condition $u(0)=v(0)=1$![]() admitting an NMS-ED that is not a uniform MS-ED.
admitting an NMS-ED that is not a uniform MS-ED.
Acknowledgements
Hailong Zhu was supported by the National NSF of China (NO. 11671118) and NSF of Anhui Province of China (no. KJ2017A432, no. KJ2018A0437).