This paper establishes the main features of the spectral theory for the singular two-point boundary-value problem 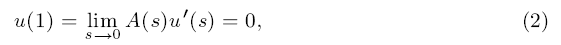and which models the buckling of a rod whose cross-sectional area decays to zero at one end. The degree of tapering is related to the rate at which the coefficient A tends to zero as s approaches 0. We say that there is tapering of order p ≥ 0 when A ∈ C([0, 1]) with A(s) > 0 for s ∈ (0, 1] and there is a constant L ∈ (0, ∞) such that lims→0A(s)/sp = L. A rigorous spectral theory involves relating (1)−(3) to the spectrum of a linear operator in a function space and then investigating the spectrum of that operator. We do this in two different (but, as we show, equivalent) settings, each of which is natural from a certain point of view. The main conclusion is that the spectral properties of the problem for tapering of order p = 2 are very different from what occurs for p < 2. For p = 2, there is a non-trivial essential spectrum and possibly no eigenvalues, whereas for p < 2, the whole spectrum consists of a sequence of simple eigenvalues. Establishing the details of this spectral theory is an important step in the study of the corresponding nonlinear model. The first function space that we choose is the one best suited to the mechanical interpretation of the problem and the one that is used for treating the nonlinear problem. However, we relate this formulation in a precise way to the usual L2 setting that is most common when dealing with boundary-value problems.