Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T22:01:16.288Z Has data issue: false hasContentIssue false
  • English
  • Français

On the exponential behaviour of eigenfunctions and the essential spectrum of differential operators

Published online by Cambridge University Press:  14 November 2011

F. V. Atkinson  and
W. D. Evans
F. V. Atkinson
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada
W. D. Evans
Affiliation:
Department of Pure Mathematics, University College, Cardiff, Wales, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The paper deals with the differential equation

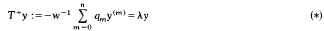
on [ 0, ∞) Where λ>0 and the coefficients qm are complex-valued with qn continuous and non-zero, w is positive and continuous and qm for m = 0, 1,…, n − 1. In the first part of the paper the exponential behaviour of any solution of (*) is given in terms of a function ρ(λ) which is roughly the distance of λ from the essential spectrum of a closed, densely denned linear operator T generated by T+ in L2(0, ∞ w). Next, estimates are obtained for the solutions in terms of the coefficients in (*). When the latter results are compared with the estimates established previously in terms of ρ(λ), bounds for ρ(λ) are obtained. From the general result there are two kinds of consequences. In the first, criteria for ρ(λ) = 0 for all All λ > 0 are obtained; this means that [0, ∞) lies in the essential spectrum of T in appropriate circumstances. The second type of consequence concerns bounds of the form ρ(λ) = O(λr) for λ → ∞ and r<1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 92 , Issue 3-4 , 1982 , pp. 271 - 300
Copyright
Copyright © Royal Society of Edinburgh 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Exponential behaviour of eigenfunctions and gaps in the essential spectrum. Lecture Notes in Mathematics 827, 1–24. (Berlin: Springer 1978).Google Scholar
2Eastham, M. S. P.. Gaps in the essential spectrum associated with singular differential operators. Quart. J. Math. Oxford 18 (1967), 155–168.CrossRefGoogle Scholar
3Eastham, M. S. P.. Gaps in the essential spectrum of even-order self-adjoint differential operators. Proc. London Math. Soc. 34 (1977), 213–230.CrossRefGoogle Scholar
4Galindo, A.. On the existence of J-self-adjoint extensions of J-symmetric operators with adjoint. Comm. Pure Appl. Math. 15 (1962), 423–425.CrossRefGoogle Scholar
5Glazman, I. M.. Direct Methods of Qualitative Spectral Analysis of Singular Differential Operator (Jerusalem: Israel Program for Scientific Translations, 1965).Google Scholar
6Gustafson, K. and Weidmann, J.. On the essential spectrum. J. Math. Anal. Appl. 25 (1969), 121–127.CrossRefGoogle Scholar
7Harris, B. J.. Gaps in the essential spectra of Schrödinger and Dirac operators. J. London Math. Soc. 18 (1978), 489–501.CrossRefGoogle Scholar
8Hartman, P. and Putnam, C. R.. The gaps in the essential spectra of wave equations. Amer. J. Math. 72 (1950), 849–862.CrossRefGoogle Scholar
9Hartman, P.. On bounded Green's kernels for second-order linear ordinary differential equations. Amer. J. Math. 73 (1951), 646–656.CrossRefGoogle Scholar
10Hartman, P.. Ordinary Differential Equations (New York: Wiley, 1964).Google Scholar
11Putnam, C. R.. On isolated eigenfunctions associated with bounded potentials. Amer. J. Math. 82 (1950), 135–147.CrossRefGoogle Scholar
12Schechter, M.. Spectra of Partial Differential Operators (London: North-Holland, 1971).Google Scholar
13Wolf, F.. On the essential spectrum of partial differential boundary problems. Comm. Pure Appl. Math. 12 (1959), 211–228.CrossRefGoogle Scholar