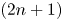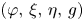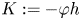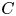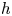1. Introduction
The study on both extrinsic and intrinsic geometry of submanifolds in the unit sphere is always an interesting topic, in which the classification research under suitable geometric conditions plays a significant role and has attracted many geometers. It is well known that, as a real hypersurface of the complex Euclidean space $\mathbb {C}^{n+1}$![]() , the unit sphere $\mathbb {S}^{2n+1}$
, the unit sphere $\mathbb {S}^{2n+1}$![]() of dimension $(2n+1)$
of dimension $(2n+1)$![]() naturally admits a Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$
naturally admits a Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$![]() (cf. [Reference Tanno30]). Moreover, an $m$
(cf. [Reference Tanno30]). Moreover, an $m$![]() -dimensional submanifold $M^m$
-dimensional submanifold $M^m$![]() in $\mathbb {S}^{2n+1}$
in $\mathbb {S}^{2n+1}$![]() is said to be $C$
is said to be $C$![]() -totally real (or equivalently, integral ) if the contact form $\eta$
-totally real (or equivalently, integral ) if the contact form $\eta$![]() of $\mathbb {S}^{2n+1}$
of $\mathbb {S}^{2n+1}$![]() vanishes when it is restricted to $M^m$
vanishes when it is restricted to $M^m$![]() , namely $\eta (X)=0$
, namely $\eta (X)=0$![]() for any $X\in TM^m$
for any $X\in TM^m$![]() . In particular, we call a $C$
. In particular, we call a $C$![]() -totally real submanifold $M^m$
-totally real submanifold $M^m$![]() Legendrian if it meets the smallest possible codimension, that is to say, $m=n$
Legendrian if it meets the smallest possible codimension, that is to say, $m=n$![]() (cf. [Reference Xing and Zhai33]), and related to the classification of such submanifolds in $\mathbb {S}^{2n+1}$
(cf. [Reference Xing and Zhai33]), and related to the classification of such submanifolds in $\mathbb {S}^{2n+1}$![]() , many results have been established in the last few decades, see e.g. [Reference Baikoussis, Blair and Koufogiorgos2, Reference Dillen and Vrancken9, Reference Hu and Xing16–Reference Lee, Lee and Vîlcu19, Reference Luo23, Reference Luo24, Reference Mihai27–Reference Sasahara29, Reference Verstraelen and Vrancken31, Reference Yin and Qi36].
, many results have been established in the last few decades, see e.g. [Reference Baikoussis, Blair and Koufogiorgos2, Reference Dillen and Vrancken9, Reference Hu and Xing16–Reference Lee, Lee and Vîlcu19, Reference Luo23, Reference Luo24, Reference Mihai27–Reference Sasahara29, Reference Verstraelen and Vrancken31, Reference Yin and Qi36].
Recently, sharpening a theorem of Yamaguchi–Kon–Ikawa [Reference Yamaguchi, Kon and Ikawa34], Cheng–He–Hu [Reference Cheng, He and Hu7] gave a complete classification of all the $n$![]() -dimensional minimal Legendrian submanifolds in Sasakian space forms with constant sectional curvature, from which it follows that
-dimensional minimal Legendrian submanifolds in Sasakian space forms with constant sectional curvature, from which it follows that
Theorem 1.1 cf. [Reference Cheng, He and Hu7]
Let $M^n$![]() $(n\ge 2)$
$(n\ge 2)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with constant sectional curvature. Then, either $M^n$
with constant sectional curvature. Then, either $M^n$![]() is the totally geodesic sphere, or $M^n$
is the totally geodesic sphere, or $M^n$![]() is the flat Clifford torus.
is the flat Clifford torus.
Regarding theorem 1.1, we see that a Legendrian submanifold $M^n$![]() in the unit sphere $\mathbb {S}^{2n+1}$
in the unit sphere $\mathbb {S}^{2n+1}$![]() is called minimal if its mean curvature $H$
is called minimal if its mean curvature $H$![]() vanishes identically, while the Clifford torus is given by the immersion $T^n\to \mathbb {S}^{2n+1}$
vanishes identically, while the Clifford torus is given by the immersion $T^n\to \mathbb {S}^{2n+1}$![]() with the parameterization as in (1.2) of [Reference Cheng, He and Hu7], where $T^n=\mathbb {S}^1\times \cdots \times \mathbb {S}^1$
with the parameterization as in (1.2) of [Reference Cheng, He and Hu7], where $T^n=\mathbb {S}^1\times \cdots \times \mathbb {S}^1$![]() and $\mathbb {S}^1$
and $\mathbb {S}^1$![]() is a circle of radius $1$
is a circle of radius $1$![]() . It was shown by direct calculation that the Clifford torus is a minimal Legendrian submanifold with flat induced metric.
. It was shown by direct calculation that the Clifford torus is a minimal Legendrian submanifold with flat induced metric.
It is worth mentioning that various attempts to generalize the above theorem have been made by geometers under suitable extrinsic and intrinsic conditions. For instance, except the examples in theorem 1.1, Xing–Zhai [Reference Xing and Zhai33] obtained new ones constructed by the Calabi product (cf. [Reference Li and Wang22]), when classifying $n$![]() -dimensional minimal Legendrian submanifolds with $C$
-dimensional minimal Legendrian submanifolds with $C$![]() -parallel second fundamental form in cases $n=3,\,4$
-parallel second fundamental form in cases $n=3,\,4$![]() , where the second fundamental form $h$
, where the second fundamental form $h$![]() of $M^n\to \mathbb {S}^{2n+1}$
of $M^n\to \mathbb {S}^{2n+1}$![]() is called $C$
is called $C$![]() -parallel if it satisfies $\bar \nabla ^\xi h=0$
-parallel if it satisfies $\bar \nabla ^\xi h=0$![]() on $M^n$
on $M^n$![]() . Moreover, compact minimal Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$
. Moreover, compact minimal Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$![]() with non-negative sectional curvature have been studied by Dillen–Vrancken [Reference Dillen and Vrancken8] for $n=3$
with non-negative sectional curvature have been studied by Dillen–Vrancken [Reference Dillen and Vrancken8] for $n=3$![]() and Zhai–Zhang [Reference Zhai and Zhang38] for $n=4$
and Zhai–Zhang [Reference Zhai and Zhang38] for $n=4$![]() , and were completely classified by Cheng–Hu [Reference Cheng and Hu5] for $n\ge 5$
, and were completely classified by Cheng–Hu [Reference Cheng and Hu5] for $n\ge 5$![]() . Meanwhile, a condition on the Ricci tensor ${\rm Ric}$
. Meanwhile, a condition on the Ricci tensor ${\rm Ric}$![]() called parallel Ricci tensor, i.e. $\nabla {\rm Ric}=0$
called parallel Ricci tensor, i.e. $\nabla {\rm Ric}=0$![]() with $\nabla$
with $\nabla$![]() being the Levi-Civita connection, has been applied by Hu–Li–Xing [Reference Hu, Li and Xing12] to successfully classify natural subclasses of such minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$
being the Levi-Civita connection, has been applied by Hu–Li–Xing [Reference Hu, Li and Xing12] to successfully classify natural subclasses of such minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() for $n=3,\,4$
for $n=3,\,4$![]() , where it is clear that the parallel Ricci tensor is a natural extension of the Einstein condition, i.e. ${\rm Ric}=\kappa g$
, where it is clear that the parallel Ricci tensor is a natural extension of the Einstein condition, i.e. ${\rm Ric}=\kappa g$![]() with $\kappa$
with $\kappa$![]() a constant and $g$
a constant and $g$![]() the induced metric. In particular, during this process, there is always an open problem that can be stated as follows:
the induced metric. In particular, during this process, there is always an open problem that can be stated as follows:
Problem Classify conformally flat minimal Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$![]() for $n\ge 3$
for $n\ge 3$![]() .
.
Some facts about the above problem are as follows. First of all, a Riemannian manifold $(M^n,\,g)$![]() is said to be conformally flat if there exists a coordinate chart $\{(U_\alpha,\,\phi _\alpha ); \,\alpha \in \Lambda \}$
is said to be conformally flat if there exists a coordinate chart $\{(U_\alpha,\,\phi _\alpha ); \,\alpha \in \Lambda \}$![]() covering $M^n$
covering $M^n$![]() such that $(\phi ^{-1}_\alpha )^*g=\rho _\alpha {\rm d}s^2$
such that $(\phi ^{-1}_\alpha )^*g=\rho _\alpha {\rm d}s^2$![]() for each $\alpha \in \Lambda$
for each $\alpha \in \Lambda$![]() , where ${\rm d}s^2$
, where ${\rm d}s^2$![]() denotes the Euclidean metric on $\mathbb {R}^n$
denotes the Euclidean metric on $\mathbb {R}^n$![]() and $\rho _\alpha$
and $\rho _\alpha$![]() is a positive function defined on $\mathbb {R}^n$
is a positive function defined on $\mathbb {R}^n$![]() . It is well known that a Riemannian surface is always conformally flat. In higher dimensions, $(M^n,\,g)$
. It is well known that a Riemannian surface is always conformally flat. In higher dimensions, $(M^n,\,g)$![]() of dimension $n\ge 4$
of dimension $n\ge 4$![]() is conformally flat if and only if its Weyl curvature tensor vanishes identically, while $(M^3,\,g)$
is conformally flat if and only if its Weyl curvature tensor vanishes identically, while $(M^3,\,g)$![]() is conformally flat if and only if its Schouten tensor is a Codazzi tensor, where the Weyl curvature tensor of $M^3$
is conformally flat if and only if its Schouten tensor is a Codazzi tensor, where the Weyl curvature tensor of $M^3$![]() vanishes automatically.
vanishes automatically.
Next, as a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with non-constant sectional curvature, the Calabi torus was characterized on the pinching conditions of the sectional curvature by Dillen–Vrancken [Reference Dillen and Vrancken8], the Ricci tensor by Hu–Xing [Reference Hu and Xing14], and the scalar curvature by Luo–Sun [Reference Luo and Sun25], Luo–Sun–Yin [Reference Luo, Sun and Yin26], respectively.
with non-constant sectional curvature, the Calabi torus was characterized on the pinching conditions of the sectional curvature by Dillen–Vrancken [Reference Dillen and Vrancken8], the Ricci tensor by Hu–Xing [Reference Hu and Xing14], and the scalar curvature by Luo–Sun [Reference Luo and Sun25], Luo–Sun–Yin [Reference Luo, Sun and Yin26], respectively.
Example 1.2 The Calabi torus in the unit sphere $\mathbb {S}^{2n+1}$![]() (cf. [Reference Luo, Sun and Yin26]).
(cf. [Reference Luo, Sun and Yin26]).
Let $\gamma =(\gamma _1,\,\gamma _2):\mathbb {S}^1\to \mathbb {S}^3\subset \mathbb {C}^2$![]() be a Legendrian curve, defined by
be a Legendrian curve, defined by

and $\phi :\mathbb {S}^{n-1}\to \mathbb {S}^{2n-1}\subset \mathbb {C}^n$![]() the totally geodesic Legendrian sphere for $n\geq 3$
the totally geodesic Legendrian sphere for $n\geq 3$![]() . Then
. Then
is a minimal Legendrian immersion and $f(\mathbb {S}^1\times \mathbb {S}^{n-1})$![]() is called the Calabi torus.
is called the Calabi torus.
In this paper, towards the above problem, we study the classification of conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() under some suitable extrinsic and intrinsic conditions. As the first of our main results, motivated by above results, we completely classify such submanifolds with semi-parallel tensor $K$
under some suitable extrinsic and intrinsic conditions. As the first of our main results, motivated by above results, we completely classify such submanifolds with semi-parallel tensor $K$![]() , namely $R\cdot K=0$
, namely $R\cdot K=0$![]() with $R$
with $R$![]() being the Riemannian curvature tensor, as a generalization of $C$
being the Riemannian curvature tensor, as a generalization of $C$![]() -parallel second fundamental form, where $K:TM^n\times TM^n\to TM^n$
-parallel second fundamental form, where $K:TM^n\times TM^n\to TM^n$![]() is a $(1,\,2)$
is a $(1,\,2)$![]() -tensor defined by $K:=-\varphi h$
-tensor defined by $K:=-\varphi h$![]() satisfying $h(X,\,Y)=\varphi K(X,\,Y)$
satisfying $h(X,\,Y)=\varphi K(X,\,Y)$![]() for any $X,\,Y\in TM^n$
for any $X,\,Y\in TM^n$![]() (see § 2.3 for details).
(see § 2.3 for details).
Theorem 1.3 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . If $M^n$
. If $M^n$![]() is of semi-parallel tensor $K$
is of semi-parallel tensor $K$![]() , then it is locally congruent to one of the following three examples:
, then it is locally congruent to one of the following three examples:
(a) $M^n$
 is the totally geodesic sphere;
is the totally geodesic sphere;(b) $M^n$
 is the flat Clifford torus;
is the flat Clifford torus;(c) $M^n$
 is the Calabi torus.
is the Calabi torus.
Remark 1.4 In order to generalize theorem 1.1, Hu–Li–Xing [Reference Hu, Li and Xing12] investigated minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() with Einstein-induced metric and verified that each of such submanifolds must be of constant sectional curvature in case of $n=4$
with Einstein-induced metric and verified that each of such submanifolds must be of constant sectional curvature in case of $n=4$![]() .
.
Recall that, for an $n$![]() -dimensional Riemannian manifold $(M^n,\,g)$
-dimensional Riemannian manifold $(M^n,\,g)$![]() , the traceless Ricci tensor $\tilde {\rm Ric}$
, the traceless Ricci tensor $\tilde {\rm Ric}$![]() of $M^n$
of $M^n$![]() is defined by $\tilde {\rm Ric}(X,\,Y)={\rm Ric}(X,\,Y)-(n-1)\chi g(X,\,Y)$
is defined by $\tilde {\rm Ric}(X,\,Y)={\rm Ric}(X,\,Y)-(n-1)\chi g(X,\,Y)$![]() for $X,\,Y\in TM^n$
for $X,\,Y\in TM^n$![]() , where ${\rm Ric}$
, where ${\rm Ric}$![]() and $\chi$
and $\chi$![]() are the Ricci tensor and normalized scalar curvature of $M^n$
are the Ricci tensor and normalized scalar curvature of $M^n$![]() , respectively. Let $\|\tilde {\rm Ric}\|$
, respectively. Let $\|\tilde {\rm Ric}\|$![]() be the tensorial norm of $\tilde {\rm Ric}$
be the tensorial norm of $\tilde {\rm Ric}$![]() with respect to the metric $g$
with respect to the metric $g$![]() . Applying theorem 1.3, we can prove the following two rigidity theorems.
. Applying theorem 1.3, we can prove the following two rigidity theorems.
Corollary 1.5 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() . Then, for its traceless Ricci tensor $\tilde {\rm Ric}$
. Then, for its traceless Ricci tensor $\tilde {\rm Ric}$![]() , it holds the pointwise inequality:
, it holds the pointwise inequality:
where $S$![]() and $\chi$
and $\chi$![]() are the squared norm of the second fundamental form and the normalized scalar curvature of $M^n$
are the squared norm of the second fundamental form and the normalized scalar curvature of $M^n$![]() , respectively. Moreover, the equality in (1.3) holds identically if and only if $M^n$
, respectively. Moreover, the equality in (1.3) holds identically if and only if $M^n$![]() is locally congruent to one of the examples (a)–(c) as in theorem 1.3.
is locally congruent to one of the examples (a)–(c) as in theorem 1.3.
Corollary 1.6 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a closed minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a closed minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with vanishing Weyl curvature tensor. Then, for its traceless Ricci tensor $\tilde {\rm Ric}$
with vanishing Weyl curvature tensor. Then, for its traceless Ricci tensor $\tilde {\rm Ric}$![]() , it holds the integral inequality:
, it holds the integral inequality:
where $S$![]() and $\chi$
and $\chi$![]() are the squared norm of the second fundamental form and the normalized scalar curvature of $M^n$
are the squared norm of the second fundamental form and the normalized scalar curvature of $M^n$![]() , respectively. Moreover, the equality in (1.4) holds if and only if $M^n$
, respectively. Moreover, the equality in (1.4) holds if and only if $M^n$![]() is locally congruent to one of the examples (a)–(c) as in theorem 1.3.
is locally congruent to one of the examples (a)–(c) as in theorem 1.3.
On the contrary, for the Riemannian manifold $(M^n,\,g)$![]() , its Ricci tensor Ric is said to be semi-parallel if and only if $R\cdot {\rm Ric}=0$
, its Ricci tensor Ric is said to be semi-parallel if and only if $R\cdot {\rm Ric}=0$![]() on $M^n$
on $M^n$![]() . This condition is obviously weaker than that of parallel Ricci tensor, as stated above. Then, the second main result of this paper can be given by
. This condition is obviously weaker than that of parallel Ricci tensor, as stated above. Then, the second main result of this paper can be given by
Theorem 1.7 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . If $M^n$
. If $M^n$![]() is of semi-parallel Ricci tensor, then it is locally congruent to one of the following three cases:
is of semi-parallel Ricci tensor, then it is locally congruent to one of the following three cases:
(a) $M^n$
 is the totally geodesic sphere;
is the totally geodesic sphere;(b) $M^n$
 is the flat Clifford torus;
is the flat Clifford torus;(c) $M^n$
 is the Calabi torus.
is the Calabi torus.
Remark 1.8 By means of theorem 1.7 and the calculations given in § 3, we see that, for the conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() , the Ricci tensor Ric is semi-parallel if and only if it is parallel, although such equivalence does not hold for general Riemannian manifolds.
, the Ricci tensor Ric is semi-parallel if and only if it is parallel, although such equivalence does not hold for general Riemannian manifolds.
Finally, we further prove the following result, by which we can complete the proofs of theorems 1.3 and 1.7, respectively.
Theorem 1.9 Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . If $(M^n,\,g)$
. If $(M^n,\,g)$![]() is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$
is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() , where $I\subset \mathbb {R}$
, where $I\subset \mathbb {R}$![]() , $g$
, $g$![]() is the induced metric on $M^n$
is the induced metric on $M^n$![]() and $(M_2,\,g_2)$
and $(M_2,\,g_2)$![]() has constant sectional curvature $c\ne 0$
has constant sectional curvature $c\ne 0$![]() , then $M^n$
, then $M^n$![]() is locally congruent to the Calabi torus.
is locally congruent to the Calabi torus.
The outline of this paper is as follows: in § 2, we give a brief review of the local theory of Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$![]() with the Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$
with the Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$![]() , and then collect necessary material on the conformally flat structure of Riemannian manifolds. For better illustrating our results, we compute in § 3 the invariants of Calabi torus with details. Section 4 is dedicated to studying the properties of Legendrian submanifolds under some certain geometric conditions. In § 5, applying these properties, we complete the proofs of theorems 1.3–1.9 and corollaries 1.5 and 1.6.
, and then collect necessary material on the conformally flat structure of Riemannian manifolds. For better illustrating our results, we compute in § 3 the invariants of Calabi torus with details. Section 4 is dedicated to studying the properties of Legendrian submanifolds under some certain geometric conditions. In § 5, applying these properties, we complete the proofs of theorems 1.3–1.9 and corollaries 1.5 and 1.6.
2. Preliminaries
In this section, we first collect some necessary material on Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$![]() of the unit sphere $\mathbb {S}^{2n+1}$
of the unit sphere $\mathbb {S}^{2n+1}$![]() that can be regarded as a Sasakian space form with constant $\varphi$
that can be regarded as a Sasakian space form with constant $\varphi$![]() -sectional curvature $1$
-sectional curvature $1$![]() . Then, we briefly review the local theory of Legendrian submanifolds in $\mathbb {S}^{2n+1}$
. Then, we briefly review the local theory of Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() . Finally, some basic notions and facts relative to conformally flat structure of Riemannian manifolds are presented for later use. For more details, we refer to [Reference Hu, Li and Xing12, Reference Hu and Yin17, Reference Xing and Yin32] and the monographs [Reference Blair3, Reference Yano and Kon35].
. Finally, some basic notions and facts relative to conformally flat structure of Riemannian manifolds are presented for later use. For more details, we refer to [Reference Hu, Li and Xing12, Reference Hu and Yin17, Reference Xing and Yin32] and the monographs [Reference Blair3, Reference Yano and Kon35].
2.1. Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$ of the unit sphere $\mathbb {S}^{2n+1}$
of the unit sphere $\mathbb {S}^{2n+1}$
As a real hypersurface of the complex Euclidean space $\mathbb {C}^{n+1}$![]() with canonical complex structure $J$
with canonical complex structure $J$![]() , the $(2n+1)$
, the $(2n+1)$![]() -dimensional unit sphere $\mathbb {S}^{2n+1}$
-dimensional unit sphere $\mathbb {S}^{2n+1}$![]() naturally admits a Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$
naturally admits a Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$![]() : $\xi =J{\bar N}$
: $\xi =J{\bar N}$![]() is the structure vector field with the unit normal vector field ${\bar N}$
is the structure vector field with the unit normal vector field ${\bar N}$![]() of the inclusion $\mathbb {S}^{2n+1} \hookrightarrow \mathbb {C}^{n+1}$
of the inclusion $\mathbb {S}^{2n+1} \hookrightarrow \mathbb {C}^{n+1}$![]() ; $g$
; $g$![]() is the induced metric on $\mathbb {S}^{2n+1}$
is the induced metric on $\mathbb {S}^{2n+1}$![]() ; $\eta (X) =g(X,\,\xi )$
; $\eta (X) =g(X,\,\xi )$![]() and $\varphi X=JX-\langle JX,\,{\bar N}\rangle {\bar N}$
and $\varphi X=JX-\langle JX,\,{\bar N}\rangle {\bar N}$![]() for any tangent vector field $X$
for any tangent vector field $X$![]() on $\mathbb {S}^{2n+1}$
on $\mathbb {S}^{2n+1}$![]() , where $\langle \cdot,\,\cdot \rangle$
, where $\langle \cdot,\,\cdot \rangle$![]() denotes the standard Hermitian metric on $\mathbb {C}^{n+1}$
denotes the standard Hermitian metric on $\mathbb {C}^{n+1}$![]() . In particular, for any tangent vector fields $X,\,Y$
. In particular, for any tangent vector fields $X,\,Y$![]() on $\mathbb {S}^{2n+1}$
on $\mathbb {S}^{2n+1}$![]() , the Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$
, the Sasakian structure $(\varphi,\,\xi,\,\eta,\,g)$![]() of $\mathbb {S}^{2n+1}$
of $\mathbb {S}^{2n+1}$![]() satisfies the following properties:
satisfies the following properties:

where $\bar {\nabla }$![]() is the Levi-Civita connection with respect to the induced metric $g$
is the Levi-Civita connection with respect to the induced metric $g$![]() on $\mathbb {S}^{2n+1}$
on $\mathbb {S}^{2n+1}$![]() .
.
2.2. Local theory of Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$
Let $M^n$![]() be a Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() , i.e. the contact form $\eta$
, i.e. the contact form $\eta$![]() restricted to $M^n$
restricted to $M^n$![]() vanishes. Consequently, $\xi$
vanishes. Consequently, $\xi$![]() is a normal vector field over $M^n$
is a normal vector field over $M^n$![]() . Denote by $N$
. Denote by $N$![]() a unit normal vector field along $M^n$
a unit normal vector field along $M^n$![]() , and by $U,\,X,\,Y,\,Z$
, and by $U,\,X,\,Y,\,Z$![]() the tangent vector fields on $M^n$
the tangent vector fields on $M^n$![]() in the subsequent paragraphs. Then, we have the Gauss and Weingarten formulas:
in the subsequent paragraphs. Then, we have the Gauss and Weingarten formulas:
where $\nabla$![]() is the Levi-Civita connection of the induced metric on $M^n$
is the Levi-Civita connection of the induced metric on $M^n$![]() , still denoted by $g$
, still denoted by $g$![]() , $h$
, $h$![]() (resp. $A_N$
(resp. $A_N$![]() ) is the second fundamental form (resp. the shape operator with respect to $N$
) is the second fundamental form (resp. the shape operator with respect to $N$![]() ) of $M^n\to \mathbb {S}^{2n+1}$
) of $M^n\to \mathbb {S}^{2n+1}$![]() , and $\nabla ^\bot$
, and $\nabla ^\bot$![]() is the normal connection in the normal bundle $T^\perp M^n$
is the normal connection in the normal bundle $T^\perp M^n$![]() . Then, by means of (2.2) it can be verified that
. Then, by means of (2.2) it can be verified that
Note from the facts $\eta (X)=0$![]() and ${\rm d}\eta (X,\,Y)=g(X,\,\varphi Y)$
and ${\rm d}\eta (X,\,Y)=g(X,\,\varphi Y)$![]() that $\varphi$
that $\varphi$![]() maps the tangent vector fields of $M^n$
maps the tangent vector fields of $M^n$![]() to the normal vector fields in $T^\perp M^n$
to the normal vector fields in $T^\perp M^n$![]() . Applying (2.2), we further have
. Applying (2.2), we further have
and thus $g(h(X,\,Y),\,\varphi Z)$![]() is totally symmetric in $X$
is totally symmetric in $X$![]() , $Y$
, $Y$![]() , and $Z$
, and $Z$![]() :
:
It follows from (2.1), (2.3), and the Weingarten formula that
Moreover, the equations of Gauss, Ricci, and Codazzi are respectively given by
where, by definitions:

From now on, we assume that $M^n$![]() is a minimal Legendrian submanifold in the sphere $\mathbb {S}^{2n+1}$
is a minimal Legendrian submanifold in the sphere $\mathbb {S}^{2n+1}$![]() , unless otherwise stated. Contracting the Gauss equation (2.7) twice, we have
, unless otherwise stated. Contracting the Gauss equation (2.7) twice, we have
where $\chi$![]() is the normalized scalar curvature and $\|\cdot \|^2$
is the normalized scalar curvature and $\|\cdot \|^2$![]() denotes the squared norm relative to the metric $g$
denotes the squared norm relative to the metric $g$![]() . Furthermore, the Ricci identity reads:
. Furthermore, the Ricci identity reads:

where $\bar {R}$![]() is the curvature tensor of the Van der Waerden–Bortolotti connection and
is the curvature tensor of the Van der Waerden–Bortolotti connection and

As usual, the so-called local Legendre frame $\{e_1,\,\ldots,\,e_n,\,e_{1^*},\,\ldots,\,e_{n^*},\, e_{2n+1}\}$![]() along $M^n$
along $M^n$![]() can be chosen such that, restricted to $M^n$
can be chosen such that, restricted to $M^n$![]() , the vector fields $e_1,\, e_2,\,\ldots,\,e_n$
, the vector fields $e_1,\, e_2,\,\ldots,\,e_n$![]() are orthonormal and tangent to $M^n$
are orthonormal and tangent to $M^n$![]() , whereas $\{e_{1^*}=\varphi e_1,\,\ldots,\, e_{n^*}=\varphi e_n,\,e_{2n+1}=\xi \}$
, whereas $\{e_{1^*}=\varphi e_1,\,\ldots,\, e_{n^*}=\varphi e_n,\,e_{2n+1}=\xi \}$![]() are the orthonormal normal vector fields of $M^n$
are the orthonormal normal vector fields of $M^n$![]() in $\mathbb {S}^{2n+1}$
in $\mathbb {S}^{2n+1}$![]() . In the sequel, we shall make the following convention on range of indices:
. In the sequel, we shall make the following convention on range of indices:
Set $h^{k^*}_{ij}=g(h(e_i,\,e_j),\,\varphi e_k)$![]() and $h^{2n+1}_{ij}=g(h(e_i,\,e_j),\,e_{2n+1})$
and $h^{2n+1}_{ij}=g(h(e_i,\,e_j),\,e_{2n+1})$![]() . Denote by $h^{\alpha ^*}_{ij,\ell }$
. Denote by $h^{\alpha ^*}_{ij,\ell }$![]() and $h^{\alpha ^*}_{ij,\ell m}$
and $h^{\alpha ^*}_{ij,\ell m}$![]() the first and the second covariant derivatives of $h^{\alpha ^*}_{ij}$
the first and the second covariant derivatives of $h^{\alpha ^*}_{ij}$![]() with respect to $\bar \nabla$
with respect to $\bar \nabla$![]() , respectively. Let $R_{ijk\ell }=g(R(e_i,\,e_j)e_\ell,\,e_k)$
, respectively. Let $R_{ijk\ell }=g(R(e_i,\,e_j)e_\ell,\,e_k)$![]() and $R_{ij\alpha ^*\beta ^*}=g(R^\perp (e_i,\, e_j)e_{\beta ^*},\,e_{\alpha ^*})$
and $R_{ij\alpha ^*\beta ^*}=g(R^\perp (e_i,\, e_j)e_{\beta ^*},\,e_{\alpha ^*})$![]() be the components of the curvature tensors of $\nabla$
be the components of the curvature tensors of $\nabla$![]() and $\nabla ^\perp$
and $\nabla ^\perp$![]() . Denote by $R_{ij}=\sum _kg(R(e_i,\,e_k)e_k,\,e_j)$
. Denote by $R_{ij}=\sum _kg(R(e_i,\,e_k)e_k,\,e_j)$![]() the components of the Ricci tensor of $g$
the components of the Ricci tensor of $g$![]() . As $M^n$
. As $M^n$![]() is minimal in $\mathbb {S}^{2n+1}$
is minimal in $\mathbb {S}^{2n+1}$![]() , it is known from (2.5)–(2.9) that
, it is known from (2.5)–(2.9) that
In this situation, the Ricci identity (2.11) can be rewritten as follows:
Finally, the following uniqueness theorem for the Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$![]() is also needed.
is also needed.
Theorem 2.1 (cf. [Reference Hu, Li and Xing12])
Let $f$![]() and $\bar {f}:M^n\to \mathbb {S}^{2n+1}$
and $\bar {f}:M^n\to \mathbb {S}^{2n+1}$![]() be two Legendrian immersions of a connected manifold $M^n$
be two Legendrian immersions of a connected manifold $M^n$![]() into the unit sphere $\mathbb {S}^{2n+1}$
into the unit sphere $\mathbb {S}^{2n+1}$![]() with the second fundamental forms $h$
with the second fundamental forms $h$![]() and $\bar {h}$
and $\bar {h}$![]() , respectively. Assume that
, respectively. Assume that
where $X,\,Y,\,Z$![]() are any tangent vector fields on $M^n$
are any tangent vector fields on $M^n$![]() . Then there exists an isometry $\tau$
. Then there exists an isometry $\tau$![]() of $\mathbb {S}^{2n+1}$
of $\mathbb {S}^{2n+1}$![]() such that $f=\tau \circ \bar {f}$
such that $f=\tau \circ \bar {f}$![]() .
.
2.3. Equivalent properties of parallel or semi-parallel tensor $K$
Recall that, for the Legendrian submanifold $M^n$![]() in the unit sphere $\mathbb {S}^{2n+1}$
in the unit sphere $\mathbb {S}^{2n+1}$![]() , its second fundamental form $h$
, its second fundamental form $h$![]() is said to be parallel if $\bar \nabla h=0$
is said to be parallel if $\bar \nabla h=0$![]() on $M^n$
on $M^n$![]() , and as a direct generalization, $h$
, and as a direct generalization, $h$![]() is said to be semi-parallel if $\bar {R}\cdot {h} =0$
is said to be semi-parallel if $\bar {R}\cdot {h} =0$![]() on $M^n$
on $M^n$![]() , where $\bar {R}$
, where $\bar {R}$![]() denotes the curvature tensor corresponding to the Van der Waerden–Bortolotti connection. For the latter one, it is easy to see from the Ricci identity (2.11) that, for tangent vector fields $U,\,X,\,Y,\,Z$
denotes the curvature tensor corresponding to the Van der Waerden–Bortolotti connection. For the latter one, it is easy to see from the Ricci identity (2.11) that, for tangent vector fields $U,\,X,\,Y,\,Z$![]() on $M^n$
on $M^n$![]() ,
,
which, under the Legendre frame $\{e_1,\,\ldots,\,e_n,\,e_{1^*},\,\ldots,\,e_{n^*},\,e_{2n+1}\}$![]() on $M^n$
on $M^n$![]() , is equivalent to
, is equivalent to
where $1\leq i,\,j,\,\ell,\,p\leq n$![]() and $\alpha ^*=\alpha +n$
and $\alpha ^*=\alpha +n$![]() for $1\leq \alpha \leq n+1$
for $1\leq \alpha \leq n+1$![]() .
.
In addition, associated with $\bar \nabla$![]() and $\xi$
and $\xi$![]() , a covariant differentiation $\bar \nabla ^{\xi }$
, a covariant differentiation $\bar \nabla ^{\xi }$![]() can be defined such that it acts on $h$
can be defined such that it acts on $h$![]() as
as
Under the Legendre frame on $M^n$![]() , setting $(\bar \nabla ^{\xi }h)(e_k,\,e_i,\,e_j) =\sum _\ell {\tilde {h}}^{\ell ^*}_{ij,k}e_{\ell ^*}$
, setting $(\bar \nabla ^{\xi }h)(e_k,\,e_i,\,e_j) =\sum _\ell {\tilde {h}}^{\ell ^*}_{ij,k}e_{\ell ^*}$![]() and
and
we obtain the following relations (cf. [Reference Hu and Yin17]):
In particular, $h$![]() is called $C$
is called $C$![]() -parallel if it satisfies $\bar \nabla ^\xi h=0$
-parallel if it satisfies $\bar \nabla ^\xi h=0$![]() on $M^n$
on $M^n$![]() .
.
For our purposes, we introduce the $(1,\,2)$![]() -tensor $K:TM^n\times TM^n\to TM^n$
-tensor $K:TM^n\times TM^n\to TM^n$![]() defined by $K:=-\varphi h$
defined by $K:=-\varphi h$![]() satisfying $h(X,\,Y)=\varphi K(X,\,Y)$
satisfying $h(X,\,Y)=\varphi K(X,\,Y)$![]() . A straightforward calculation shows that
. A straightforward calculation shows that
Lemma 2.2 For the tensor $K$![]() of the Legendrian submanifold $M^n$
of the Legendrian submanifold $M^n$![]() in $\mathbb {S}^{2n+1}$
in $\mathbb {S}^{2n+1}$![]() , we have
, we have
(1) $K_XY=K(X,\,Y)=A_{\varphi X}Y$
 and $g(K(X,\,Y),\,Z)$
and $g(K(X,\,Y),\,Z)$ is totally symmetric;
is totally symmetric;(2) $M^n$
 is minimal if and only if ${\rm trace}\,K_X=0$
is minimal if and only if ${\rm trace}\,K_X=0$ for any $X\in TM^n$
for any $X\in TM^n$ ;
;(3) $(\nabla K)(X,\,Y,\,Z)=(\nabla K)(Y,\,X,\,Z)$
 for any $X,\,Y,\,Z\in TM^n$
for any $X,\,Y,\,Z\in TM^n$ ;
;(4) the Ricci identity for the tensor $K$
 is given by
\begin{align*} & (\nabla^2 K)(U,X,Y,Z)-(\nabla^2 K)(X,U,Y,Z)=(R\cdot K)(U,X,Y,Z)\\ & =R(U,X)K(Y,Z)-K(R(U,X)Y,Z)-K(Y,R(U,X)Z), \end{align*}where $(\nabla ^2 K)(U,\,X,\,Y,\,Z)=(\nabla _U(\nabla K))(X,\,Y,\,Z)$
is given by
\begin{align*} & (\nabla^2 K)(U,X,Y,Z)-(\nabla^2 K)(X,U,Y,Z)=(R\cdot K)(U,X,Y,Z)\\ & =R(U,X)K(Y,Z)-K(R(U,X)Y,Z)-K(Y,R(U,X)Z), \end{align*}where $(\nabla ^2 K)(U,\,X,\,Y,\,Z)=(\nabla _U(\nabla K))(X,\,Y,\,Z)$
 for any $U,\,X,\,Y,\,Z\in TM^n$
for any $U,\,X,\,Y,\,Z\in TM^n$ .
.
Furthermore, it can be checked by using (2.20) and (2.21) that

Consequently, $\nabla K=0$![]() if and only if $\bar \nabla ^\xi h=0$
if and only if $\bar \nabla ^\xi h=0$![]() , and $R\cdot K=0$
, and $R\cdot K=0$![]() if and only if
if and only if
which, under the Legendre frame $\{e_1,\,\ldots,\,e_n,\,e_{1^*},\,\ldots,\,e_{n^*},\, e_{2n+1}\}$![]() on $M^n$
on $M^n$![]() , is equivalent to
, is equivalent to
Here, we shall call the tensor $K$![]() parallel (resp. semi-parallel ) if $\nabla K=0$
parallel (resp. semi-parallel ) if $\nabla K=0$![]() (resp. $R\cdot K=0$
(resp. $R\cdot K=0$![]() ) holds on $M^n$
) holds on $M^n$![]() .
.
Lemma 2.3 Let $M^n$![]() $(n\ge 2)$
$(n\ge 2)$![]() be a Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, $M^n$
. Then, $M^n$![]() is of $C$
is of $C$![]() -parallel second fundamental form if and only if $\nabla K=0$
-parallel second fundamental form if and only if $\nabla K=0$![]() on $M^n$
on $M^n$![]() , where $\nabla$
, where $\nabla$![]() denotes the Levi-Civita connection, and $M^n$
denotes the Levi-Civita connection, and $M^n$![]() satisfies equation (2.24) if and only if $R\cdot K=0$
satisfies equation (2.24) if and only if $R\cdot K=0$![]() on $M^n$
on $M^n$![]() , where $R$
, where $R$![]() denotes the curvature tensor of the connection $\nabla$
denotes the curvature tensor of the connection $\nabla$![]() .
.
Assume that the tensor $K$![]() of Legendrian submanifold $M^n$
of Legendrian submanifold $M^n$![]() does not vanish at some point $x\in M^n$
does not vanish at some point $x\in M^n$![]() . We shall consider $U_{x}M^n=\{v\in T_xM^n\,|\,g(v,\,v)=1\}$
. We shall consider $U_{x}M^n=\{v\in T_xM^n\,|\,g(v,\,v)=1\}$![]() and then define a function $F$
and then define a function $F$![]() on $U_xM^n$
on $U_xM^n$![]() by $F(u):=g(K(u,\,u),\,u)=g(A_{\varphi u}u,\,u)$
by $F(u):=g(K(u,\,u),\,u)=g(A_{\varphi u}u,\,u)$![]() for $u\in U_xM^n$
for $u\in U_xM^n$![]() . Since $U_xM^n$
. Since $U_xM^n$![]() is compact, there exists a unit vector $e_1\in U_xM^n$
is compact, there exists a unit vector $e_1\in U_xM^n$![]() at which the function $F(u)$
at which the function $F(u)$![]() attains an absolute maximum, denoted by $\lambda _1$
attains an absolute maximum, denoted by $\lambda _1$![]() and $\lambda _1>0$
and $\lambda _1>0$![]() . As a result, it holds that:
. As a result, it holds that:
Lemma 2.4 (cf. [Reference Hu, Li and Xing12]; Lemma 5.1 and Corollary 5.1 of [Reference Hu, Li and Vrancken11])
There exists an orthonormal basis $\{e_1,\,\ldots,\,e_n\}$![]() of $T_xM^n$
of $T_xM^n$![]() so that $K_{e_1}e_i =\lambda _ie_i$
so that $K_{e_1}e_i =\lambda _ie_i$![]() for $1\le i\le n$
for $1\le i\le n$![]() , where $\lambda _1$
, where $\lambda _1$![]() is the maximum value of $F$
is the maximum value of $F$![]() on $U_xM^n$
on $U_xM^n$![]() . Also, $\lambda _1\ge 2\lambda _i$
. Also, $\lambda _1\ge 2\lambda _i$![]() for $i\ge 2$
for $i\ge 2$![]() , and if $\lambda _1=2\lambda _j$
, and if $\lambda _1=2\lambda _j$![]() for some $j\ge 2$
for some $j\ge 2$![]() , then $F(e_j)=0$
, then $F(e_j)=0$![]() . Moreover, for a unit vector $u\in T_xM^n$
. Moreover, for a unit vector $u\in T_xM^n$![]() , if $K_uu=\lambda u$
, if $K_uu=\lambda u$![]() , then $\lambda$
, then $\lambda$![]() is an extremal value of the function $F$
is an extremal value of the function $F$![]() on $U_xM^n$
on $U_xM^n$![]() .
.
2.4. Conformally flat Riemannian manifolds and product manifolds
Let $(M^n,\,g)$![]() be an $n$
be an $n$![]() -dimensional connected Riemannian manifold with the normalized scalar curvature $\chi$
-dimensional connected Riemannian manifold with the normalized scalar curvature $\chi$![]() and the Levi-Civita connection $\nabla$
and the Levi-Civita connection $\nabla$![]() of the metric $g$
of the metric $g$![]() . The Schouten tensor $P$
. The Schouten tensor $P$![]() of $(1,\,1)$
of $(1,\,1)$![]() -type defined by
-type defined by
is a self-adjoint operator with respect to the metric $g$![]() , where $Q$
, where $Q$![]() and id denote the Ricci operator and the identity transformation, respectively. By definition there holds:
and id denote the Ricci operator and the identity transformation, respectively. By definition there holds:
where ${\rm Ric}$![]() denotes the Ricci tensor of $M^n$
denotes the Ricci tensor of $M^n$![]() and $X,\,Y$
and $X,\,Y$![]() are vector fields tangent to $M^n$
are vector fields tangent to $M^n$![]() .
.
Recall that $(M^n,\,g)$![]() is said to be conformally flat if around each point of $M^n$
is said to be conformally flat if around each point of $M^n$![]() there exists a neighbourhood which can be conformally immersed into the Euclidean space $\mathbb {R}^n$
there exists a neighbourhood which can be conformally immersed into the Euclidean space $\mathbb {R}^n$![]() . When $n\ge 4$
. When $n\ge 4$![]() , it is known that $(M^n,\,g)$
, it is known that $(M^n,\,g)$![]() is conformally flat if and only if its Weyl curvature tensor vanishes. In this situation, the curvature tensor $R$
is conformally flat if and only if its Weyl curvature tensor vanishes. In this situation, the curvature tensor $R$![]() of $g$
of $g$![]() can be rewritten as below:
can be rewritten as below:
where $X,\,Y,\,Z$![]() are tangent vector fields of $M^n$
are tangent vector fields of $M^n$![]() , and the Schouten tensor $P$
, and the Schouten tensor $P$![]() is Codazzi, i.e.:
is Codazzi, i.e.:
When $n=3$![]() , we should remark that the Weyl curvature tensor vanishes automatically, and $(M^3,\,g)$
, we should remark that the Weyl curvature tensor vanishes automatically, and $(M^3,\,g)$![]() is conformally flat if and only if $P$
is conformally flat if and only if $P$![]() is a Codazzi tensor as above.
is a Codazzi tensor as above.
Moreover, the Ricci tensor ${\rm Ric}$![]() of $M^n$
of $M^n$![]() is called parallel or semi-parallel if it satisfies $\nabla {\rm Ric}=0$
is called parallel or semi-parallel if it satisfies $\nabla {\rm Ric}=0$![]() or $R\cdot {\rm Ric}=0$
or $R\cdot {\rm Ric}=0$![]() . In the latter case, by definition one has:
. In the latter case, by definition one has:
In addition, we call the Riemannian manifold $(M^n,\,g)$![]() quasi-Einstein if its Ricci operator $Q$
quasi-Einstein if its Ricci operator $Q$![]() admits exactly two distinct eigenvalues at each point, one of which is simple, and the traceless Ricci tensor $\tilde {\rm Ric}$
admits exactly two distinct eigenvalues at each point, one of which is simple, and the traceless Ricci tensor $\tilde {\rm Ric}$![]() of $M^n$
of $M^n$![]() is defined by
is defined by
Finally, we recall the following theorem for later use.
Theorem 2.5 (cf. Theorem 3.7 of [Reference Brozos-Vázquez, García-Río and Vázquez-Lorenzo4])
Let $(M^n,\,g)=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() be a Riemannian product, where $I\subset \mathbb {R}$
be a Riemannian product, where $I\subset \mathbb {R}$![]() and dim $M_2\ge 2$
and dim $M_2\ge 2$![]() . Then, $(M^n,\,g)$
. Then, $(M^n,\,g)$![]() is conformally flat if and only if $(M_2,\,g_2)$
is conformally flat if and only if $(M_2,\,g_2)$![]() is a space form of constant curvature.
is a space form of constant curvature.
3. Geometric invariants of the Calabi torus
In [Reference Luo and Sun25], Luo and Sun have made some calculations about the Calabi torus in the unit sphere $\mathbb {S}^{2n+1}$![]() . In this section, in order to obtain the exact knowledge about the Calabi torus, we compute its geometric invariants with more details.
. In this section, in order to obtain the exact knowledge about the Calabi torus, we compute its geometric invariants with more details.
Proposition 3.1 The Calabi torus in the unit sphere $\mathbb {S}^{2n+1}$![]() with the immersion given by $f$
with the immersion given by $f$![]() as in example 1.2 is indeed a minimal Legendrian submanifold with $C$
as in example 1.2 is indeed a minimal Legendrian submanifold with $C$![]() -parallel second fundamental form and conformally flat induced metric for $n\geq 3$
-parallel second fundamental form and conformally flat induced metric for $n\geq 3$![]() , satisfying the identity:
, satisfying the identity:
where $\tilde {\rm Ric}$![]() is the traceless Ricci tensor, $S$
is the traceless Ricci tensor, $S$![]() is the squared norm of the second fundamental form, and $\chi$
is the squared norm of the second fundamental form, and $\chi$![]() is the normalized scalar curvature. In particular, the Calabi torus is quasi-Einstein and its Ricci tensor is parallel with respect to the Levi-Civita connection.
is the normalized scalar curvature. In particular, the Calabi torus is quasi-Einstein and its Ricci tensor is parallel with respect to the Levi-Civita connection.
Proof. Note from the induced metric of $f(t,\,y):\mathbb {S}^1\times \mathbb {S}^{n-1}\to \mathbb {S}^{2n+1}\subset \mathbb {C}^{n+1}$![]() :
:
that $f$![]() is an isometric immersion, where $y=(y_1,\,\ldots,\,y_n)\in \mathbb {S}^{n-1} \subset \mathbb {R}^n$
is an isometric immersion, where $y=(y_1,\,\ldots,\,y_n)\in \mathbb {S}^{n-1} \subset \mathbb {R}^n$![]() and $\sum ^n_{i=1}y^2_i=1$
and $\sum ^n_{i=1}y^2_i=1$![]() . Adopting the following local reparametrization:
. Adopting the following local reparametrization:
we obtain a local orthonormal frame $\{e_i\}^n_{i=1}$![]() on $f(\mathbb {S}^1\times \mathbb {S}^{n-1})=:M^n$
on $f(\mathbb {S}^1\times \mathbb {S}^{n-1})=:M^n$![]() with respect to the metric $g$
with respect to the metric $g$![]() , satisfying the relations:
, satisfying the relations:

As the unit sphere $\mathbb {S}^{2n+1}$![]() admits a natural Sasakian structure $(\varphi,\, \xi,\,\eta,\,g)$
admits a natural Sasakian structure $(\varphi,\, \xi,\,\eta,\,g)$![]() , by definition we see that $\eta (e_i)=0$
, by definition we see that $\eta (e_i)=0$![]() for $1\leq i\leq n$
for $1\leq i\leq n$![]() and thus $f$
and thus $f$![]() is a Legendrian immersion.
is a Legendrian immersion.
Denote by $h$![]() the second fundamental form of $f:\mathbb {S}^1\times \mathbb {S}^{n-1}\to \mathbb {S}^{2n+1}$
the second fundamental form of $f:\mathbb {S}^1\times \mathbb {S}^{n-1}\to \mathbb {S}^{2n+1}$![]() . Then, direct calculations by using the Gauss formula show that (cf. [Reference Hu, Li and Xing12]):
. Then, direct calculations by using the Gauss formula show that (cf. [Reference Hu, Li and Xing12]):

where $\nabla$![]() denotes the Levi-Civita connection of the metric $g$
denotes the Levi-Civita connection of the metric $g$![]() , and
, and
It is obvious that such an immersion $f$![]() is minimal. Combining with (3.3) and (3.4), we further conclude from (2.4) and (2.20) that $({\bar \nabla }^{\xi }h)(e_i,\,e_j,\,e_k)=0$
is minimal. Combining with (3.3) and (3.4), we further conclude from (2.4) and (2.20) that $({\bar \nabla }^{\xi }h)(e_i,\,e_j,\,e_k)=0$![]() holds for $1\leq i,\,j,\,k\leq n$
holds for $1\leq i,\,j,\,k\leq n$![]() , i.e. the immersion $f$
, i.e. the immersion $f$![]() is of $C$
is of $C$![]() -parallel second fundamental form.
-parallel second fundamental form.
For the Riemannian curvature tensor of $M^n$![]() , applying (3.3) again, we easily get:
, applying (3.3) again, we easily get:

Therefore, we obtain from (3.4) and (3.5) that

and then (3.1) follows from (2.32). On the contrary, it is also known from (3.6) that
which shows that $(M^n,\,g)$![]() is quasi-Einstein. Moreover, with the help of (2.27), we conclude that both (2.29) and (2.30) hold. Consequently, the Weyl curvature tensor of $M^n$
is quasi-Einstein. Moreover, with the help of (2.27), we conclude that both (2.29) and (2.30) hold. Consequently, the Weyl curvature tensor of $M^n$![]() vanishes and its Schouten tensor is Codazzi, meaning that $(M^n,\, g)$
vanishes and its Schouten tensor is Codazzi, meaning that $(M^n,\, g)$![]() is conformally flat. Finally, making use of (3.3) and (3.7), we calculate that:
is conformally flat. Finally, making use of (3.3) and (3.7), we calculate that:
From this, it is easily seen that ${\rm Ric}$![]() is parallel with respect to the Levi-Civita connection $\nabla$
is parallel with respect to the Levi-Civita connection $\nabla$![]() , and hence we have completed the proof of proposition 3.1.
, and hence we have completed the proof of proposition 3.1.
4. Properties of the Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$
In this section, before completing the proofs of the main results, we will investigate the properties of the Legendrian submanifolds in the unit sphere $\mathbb {S}^{2n+1}$![]() under some certain geometric conditions.
under some certain geometric conditions.
4.1. Minimal Legendrian submanifolds
For our purposes, we first calculate the Laplacian of $S$![]() to derive the following:
to derive the following:
Lemma 4.1 Let $M^n$![]() $(n\ge 2)$
$(n\ge 2)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, it holds the identity:
. Then, it holds the identity:
where $\|{\rm Rie}\|^2$![]() denotes the squared norm of the Riemannian curvature tensor with respect to the metric $g$
denotes the squared norm of the Riemannian curvature tensor with respect to the metric $g$![]() on $M^n$
on $M^n$![]() . Moreover, if it is of semi-parallel tensor $K$
. Moreover, if it is of semi-parallel tensor $K$![]() , we further have:
, we further have:
Proof. Choose the local Legendre frame $\{e_1,\,\ldots,\,e_n,\,e_{1^*},\,\ldots,\,e_{n^*},\,e_{2n+1}\}$![]() along $M^n$
along $M^n$![]() as in § 2. By definition, we have
as in § 2. By definition, we have

Applying the Ricci identity (2.16), we deduce from (2.15) that

This together with (2.13)–(2.15) yields that

To go on from (4.6), we make use of the relation
and (2.13) to calculate that:
On the contrary, with the help of (2.14), it is easily seen that:
Substituting (4.8) and (4.9) into (4.6), we then conclude that:
As $h_{ij,\ell }^{2n+1}=h_{ij}^{\ell ^*}$![]() and $h^{k^*}_{ij,\ell }=\tilde {h}^{k^*}_{ij,\ell }$
and $h^{k^*}_{ij,\ell }=\tilde {h}^{k^*}_{ij,\ell }$![]() for any $i,\,j,\,k,\,\ell$
for any $i,\,j,\,k,\,\ell$![]() , it follows that
, it follows that
and thus we obtain (4.1) by substituting (4.10) and (4.11) into (4.4) immediately.
Now, if assuming that $M^n$![]() has semi-parallel tensor $K$
has semi-parallel tensor $K$![]() , then
, then
where we used $h^{k^*}_{ij,\ell p}=\tilde {h}^{k^*}_{ij,\ell p}-h^{\ell ^*}_{ij}\delta _{kp}$![]() and $h^{2n+1}_{ij,\ell p}=2h^{\ell ^*}_{ij,p}$
and $h^{2n+1}_{ij,\ell p}=2h^{\ell ^*}_{ij,p}$![]() . Similarly, we obtain that
. Similarly, we obtain that
which combining with (4.11) shows that
This gives (4.2) by (2.10), and substituting (4.14) into (4.1) finally yields (4.3).
Remark 4.2 It is known from (4.2) that, for closed minimal Legendrian submanifolds or minimal Legendrian submanifolds with constant scalar curvature in $\mathbb {S}^{2n+1}$![]() with $n\ge 2$
with $n\ge 2$![]() , the semi-parallelism of tensor $K$
, the semi-parallelism of tensor $K$![]() and the $C$
and the $C$![]() -parallelism of second fundamental form are equivalent.
-parallelism of second fundamental form are equivalent.
Furthermore, recalling the components of the Weyl curvature tensor $W$![]() of $M^n$
of $M^n$![]() satisfy
satisfy
we have the following expression for $n\ge 3$![]() (cf. [Reference Hu and Xing15, Reference Xing and Yin32]):
(cf. [Reference Hu and Xing15, Reference Xing and Yin32]):
where $\|W\|^2=\sum _{i,j,k,\ell }(W_{ijk\ell })^2$![]() . From $\tilde {R}_{ij}=R_{ij} -(n-1)\chi \delta _{ij}$
. From $\tilde {R}_{ij}=R_{ij} -(n-1)\chi \delta _{ij}$![]() , it is easy to see that
, it is easy to see that
Here, $\tilde {\rm Ric}$![]() is the traceless part of ${\rm Ric}$
is the traceless part of ${\rm Ric}$![]() and $\|\tilde {\rm Ric}\|^2 =\sum _{i,j}(\tilde {R}_{ij})^2$
and $\|\tilde {\rm Ric}\|^2 =\sum _{i,j}(\tilde {R}_{ij})^2$![]() . From the combination of (2.10), (4.16), and (4.17), we then derive by using (4.1) the following result:
. From the combination of (2.10), (4.16), and (4.17), we then derive by using (4.1) the following result:
Proposition 4.3 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, it holds the identity:
. Then, it holds the identity:
4.2. Conformally flat Legendrian submanifolds
Assume that $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() is a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
is a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, we shall prove that
. Then, we shall prove that
Lemma 4.4 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, for the tensor $K$
. Then, for the tensor $K$![]() and Schouten tensor $P$
and Schouten tensor $P$![]() of $M^n$
of $M^n$![]() , it holds that
, it holds that

where $U,\,X,\,Y,\,Z$![]() are vector fields tangent to $M^n$
are vector fields tangent to $M^n$![]() and $\mathop {\mathfrak {S}}$
and $\mathop {\mathfrak {S}}$![]() denotes the cyclic summation.
denotes the cyclic summation.
Proof. We begin with taking the covariant derivative of the Codazzi equation for $K$![]() along a vector field $U$
along a vector field $U$![]() tangent to $M^n$
tangent to $M^n$![]() :
:
where, according to lemma 2.2 (3), $G(X,\,Y,\,Z):=(\nabla K)(X,\,Y,\,Z)-(\nabla K) (Y, X,\,Z)=0$![]() for tangent vector fields $X,\,Y,\,Z$
for tangent vector fields $X,\,Y,\,Z$![]() on $M^n$
on $M^n$![]() . It is obvious from (4.20) that
. It is obvious from (4.20) that
Furthermore, direct calculations by using the Ricci identity show that

Finally, the assertion immediately follows by substituting (2.29) into (4.22).
Remark 4.5 The technique used to prove lemma 4.4 is called the Tsinghua principle, which was first discovered by H. Li, L. Vrancken, and X. Wang (cf. [Reference Antić, Li, Vrancken and Wang1]). Recently, this remarkable principle has been widely applied, and turns out to be very useful for various purposes, see e.g. [Reference Cheng, Hu, Moruz and Vrancken6, Reference Dioos, Vrancken and Wang10, Reference Hu, Moruz, Vrancken and Yao13, Reference Li, Xing and Xu20, Reference Li, Ma, Van der Veken, Vrancken and Wang21, Reference Zhai and Xing37].
Choosing an orthonormal frame $\{e_i\}^n_{i=1}$![]() over $M^n$
over $M^n$![]() such that $e_i$
such that $e_i$![]() is the eigenvector field of the Ricci operator $Q$
is the eigenvector field of the Ricci operator $Q$![]() with $\mu _i$
with $\mu _i$![]() the corresponding eigenvalue, by (2.27) we easily see that $Pe_i=\nu _ie_i$
the corresponding eigenvalue, by (2.27) we easily see that $Pe_i=\nu _ie_i$![]() and $\nu _i={\mu _i}/{(n-2)} -{n\chi }/{(2(n-2))}$
and $\nu _i={\mu _i}/{(n-2)} -{n\chi }/{(2(n-2))}$![]() . Without loss of generality, we shall suppose that $Q$
. Without loss of generality, we shall suppose that $Q$![]() has $t$
has $t$![]() distinct eigenvalues $\mu _1,\,\dots,\,\mu _t$
distinct eigenvalues $\mu _1,\,\dots,\,\mu _t$![]() with multiplicities $n_1,\,\dots,\,n_t$
with multiplicities $n_1,\,\dots,\,n_t$![]() , respectively. Let $\mathfrak {D}(\mu _s)$
, respectively. Let $\mathfrak {D}(\mu _s)$![]() (resp. $\mathfrak {D}(\nu _s)$
(resp. $\mathfrak {D}(\nu _s)$![]() ) denote the distribution such that $\mathfrak {D}(\mu _s)(x)$
) denote the distribution such that $\mathfrak {D}(\mu _s)(x)$![]() (resp. $\mathfrak {D}(\nu _s)(x)$
(resp. $\mathfrak {D}(\nu _s)(x)$![]() ) is the eigenspace of $\mu _s(x)$
) is the eigenspace of $\mu _s(x)$![]() (resp. $\nu _s(x)$
(resp. $\nu _s(x)$![]() ) at an arbitrary point $x\in M^n$
) at an arbitrary point $x\in M^n$![]() for $1\leq s\leq t$
for $1\leq s\leq t$![]() , and $n_1+\cdots +n_t=n$
, and $n_1+\cdots +n_t=n$![]() . For simplicity of notations, we also make the convention that, for $i\le t$
. For simplicity of notations, we also make the convention that, for $i\le t$![]() and $j\ge t+1$
and $j\ge t+1$![]() , if $\mu _j=\mu _i$
, if $\mu _j=\mu _i$![]() we shall write $n_j=n_i$
we shall write $n_j=n_i$![]() , $\mathfrak {D}(\mu _j)=\mathfrak {D}(\mu _i)$
, $\mathfrak {D}(\mu _j)=\mathfrak {D}(\mu _i)$![]() and $\mathfrak {D}(\nu _j) =\mathfrak {D}(\nu _i)$
and $\mathfrak {D}(\nu _j) =\mathfrak {D}(\nu _i)$![]() .
.
Lemma 4.6 Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, with respect to the orthonormal frame $\{e_i\}^n_{i=1}$
. Then, with respect to the orthonormal frame $\{e_i\}^n_{i=1}$![]() on $M^n$
on $M^n$![]() as above, the tensor $K$
as above, the tensor $K$![]() of $M^n$
of $M^n$![]() satisfies the following properties:
satisfies the following properties:
(1) If $\nu _i\neq \nu _j$
 and $n_i,\,n_j\geq 2$
and $n_i,\,n_j\geq 2$ , then $K(e_i,\,e_j)=0$
, then $K(e_i,\,e_j)=0$ ;
;(2) If $n_i=1$
 and $n_j\geq 2$
and $n_j\geq 2$ , then there exist functions $\lambda ^i_j$
, then there exist functions $\lambda ^i_j$ depending on the choice of $\nu _i,\,\nu _j$
depending on the choice of $\nu _i,\,\nu _j$ such that $K(e_i,\,e_j)=\lambda ^i_je_j$
such that $K(e_i,\,e_j)=\lambda ^i_je_j$ ;
;(3) If there are at least two distinct eigenvalues $\nu _j,\,\nu _k$
 such that $n_j,\,n_k\geq 2$
such that $n_j,\,n_k\geq 2$ and $n_i=1$
and $n_i=1$ , then there exists a differentiable function $\bar \lambda _i$
, then there exists a differentiable function $\bar \lambda _i$ such that it satisfies that $(\nu _i-\nu _j)\lambda ^i_j=(\nu _i-\nu _k)\lambda ^i_k=\bar \lambda _i$
such that it satisfies that $(\nu _i-\nu _j)\lambda ^i_j=(\nu _i-\nu _k)\lambda ^i_k=\bar \lambda _i$ .
.
Proof. We begin with taking the product of equation (4.19) with vector field $V$![]() and setting $U=e_k$
and setting $U=e_k$![]() , $X=e_i$
, $X=e_i$![]() , $Y=e_j$
, $Y=e_j$![]() , $Z=e_\ell$
, $Z=e_\ell$![]() , and $V=e_m$
, and $V=e_m$![]() to derive the relation:
to derive the relation:

where $1\leq i,\,j,\,k,\,\ell,\,m\leq n$![]() , and $K^m_{ij}:=g(K(e_i,\,e_j),\,e_m)$
, and $K^m_{ij}:=g(K(e_i,\,e_j),\,e_m)$![]() .
.
First of all, we assume that $\nu _i\neq \nu _j=\nu _k$![]() for distinct $i,\,j,\,k$
for distinct $i,\,j,\,k$![]() , and then $e_i \in \mathfrak {D}(\nu _i)$
, and then $e_i \in \mathfrak {D}(\nu _i)$![]() and $e_j,\,e_k\in \mathfrak {D}(\nu _j)$
and $e_j,\,e_k\in \mathfrak {D}(\nu _j)$![]() for $n_j\geq 2$
for $n_j\geq 2$![]() . Taking $m\neq j,\,k$
. Taking $m\neq j,\,k$![]() , we therefore obtain from (4.23) that
, we therefore obtain from (4.23) that
Taking $\ell =k$![]() yields that $K^m_{ij}=0$
yields that $K^m_{ij}=0$![]() , by which we see that $K(e_i,\,e_j)\in \mathfrak {D} (\nu _j)$
, by which we see that $K(e_i,\,e_j)\in \mathfrak {D} (\nu _j)$![]() for $n_j\geq 2$
for $n_j\geq 2$![]() . Similarly, $K(e_i,\,e_j)\in \mathfrak {D}(\nu _i)$
. Similarly, $K(e_i,\,e_j)\in \mathfrak {D}(\nu _i)$![]() for $n_i\geq 2$
for $n_i\geq 2$![]() . Combining with the assumption $\nu _i\neq \nu _j$
. Combining with the assumption $\nu _i\neq \nu _j$![]() , we can conclude that $K(e_i,\,e_j)=0$
, we can conclude that $K(e_i,\,e_j)=0$![]() provided that $n_i,\,n_j\geq 2$
provided that $n_i,\,n_j\geq 2$![]() . Hence, we get assertion (1).
. Hence, we get assertion (1).
Next, if $n_i=1$![]() and $n_j\geq 2$
and $n_j\geq 2$![]() , some $e_k\in \mathfrak {D}(\nu _j)$
, some $e_k\in \mathfrak {D}(\nu _j)$![]() different from $e_j$
different from $e_j$![]() can be chosen to satisfy $\nu _i\neq \nu _j=\nu _k$
can be chosen to satisfy $\nu _i\neq \nu _j=\nu _k$![]() for distinct $i,\,j,\,k$
for distinct $i,\,j,\,k$![]() . In this situation, we take $m=k$
. In this situation, we take $m=k$![]() in (4.23) to deduce that
in (4.23) to deduce that
It follows that $K^i_{jj}=K^i_{kk}$![]() for $\ell =j$
for $\ell =j$![]() , $K^k_{ij}=0$
, $K^k_{ij}=0$![]() for $\ell =k$
for $\ell =k$![]() , and moreover $K^\ell _{ij}=0$
, and moreover $K^\ell _{ij}=0$![]() for $\ell \neq j,\,k$
for $\ell \neq j,\,k$![]() . Consequently, assertion (2) follows by putting $\lambda ^i_j=K^i_{jj}$
. Consequently, assertion (2) follows by putting $\lambda ^i_j=K^i_{jj}$![]() , where $\lambda ^i_j$
, where $\lambda ^i_j$![]() does not depend on the choice of $e_k\in \mathfrak {D}(\nu _j)$
does not depend on the choice of $e_k\in \mathfrak {D}(\nu _j)$![]() .
.
Finally, for $n_i=1$![]() and $\nu _j\neq \nu _k$
and $\nu _j\neq \nu _k$![]() with $n_j,\,n_k\geq 2$
with $n_j,\,n_k\geq 2$![]() , by taking $\ell =j$
, by taking $\ell =j$![]() in (4.23) and applying assertion (1), we easily get:
in (4.23) and applying assertion (1), we easily get:
Thus, taking $m=k$![]() , and noting $\lambda ^i_j=K^i_{jj}=K_{ij}^j$
, and noting $\lambda ^i_j=K^i_{jj}=K_{ij}^j$![]() and $\lambda ^i_k=K^i_{kk} =K_{ik}^k$
and $\lambda ^i_k=K^i_{kk} =K_{ik}^k$![]() , we further have
, we further have
This verifies assertion (3). Hence, lemma 4.6 has been proved.
4.3. Conformally flat minimal Legendrian submanifolds with $R\cdot K=0$
In this subsection, we shall consider that $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() is a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
is a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() . Therefore, we obtain from lemma 2.2 (4) that
. Therefore, we obtain from lemma 2.2 (4) that
where $X,\,Y,\,Z,\,U$![]() are vector fields tangent to $M^n$
are vector fields tangent to $M^n$![]() . According to lemma 2.3, we then present the following lemma involving the number $r$
. According to lemma 2.3, we then present the following lemma involving the number $r$![]() of distinct eigenvalues of the Schouten tensor $P$
of distinct eigenvalues of the Schouten tensor $P$![]() of $M^n$
of $M^n$![]() .
.
Lemma 4.7 Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with $R\cdot K=0$
with $R\cdot K=0$![]() . Then, either $M^n$
. Then, either $M^n$![]() is of constant sectional curvature, or it is quasi-Einstein. In the latter case, the Schouten tensor of $M^n$
is of constant sectional curvature, or it is quasi-Einstein. In the latter case, the Schouten tensor of $M^n$![]() admits two distinct eigenvalues $\nu _1$
admits two distinct eigenvalues $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() at each point, where one of them is simple, such that $\nu _1+\nu _2=0$
at each point, where one of them is simple, such that $\nu _1+\nu _2=0$![]() .
.
Proof. First of all, by taking $X=e_i$![]() , $Y=e_j$
, $Y=e_j$![]() , $Z=e_k$
, $Z=e_k$![]() , and $U=e_\ell$
, and $U=e_\ell$![]() in (4.28), we can apply (2.29) to calculate the relation:
in (4.28), we can apply (2.29) to calculate the relation:

For $k=\ell =i\neq j$![]() in (4.29), it is easy to see that:
in (4.29), it is easy to see that:
Taking the inner product of (4.30) with $e_i$![]() , we then deduce from lemma 2.2 that:
, we then deduce from lemma 2.2 that:
Similarly, interchanging the roles of $e_i$![]() and $e_j$
and $e_j$![]() in (4.31) gives
in (4.31) gives
Furthermore, by taking the inner product of (4.30) with $e_j$![]() , we obtain that
, we obtain that
which together with (4.30) and (4.31) implies that
On the contrary, for $k=i\neq j=\ell$![]() in (4.29), we easily get:
in (4.29), we easily get:
This combining with (4.31) and (4.32) yields that
Next, we shall continue with the proof here by proving the following three claims.
Claim 1. If $\nu _i\neq 0$![]() and $n_i\geq 2$
and $n_i\geq 2$![]() , then $g(K(u,\,v),\,\omega )=0$
, then $g(K(u,\,v),\,\omega )=0$![]() for any $u,\,v,\,\omega \in \mathfrak {D}(\nu _i)$
for any $u,\,v,\,\omega \in \mathfrak {D}(\nu _i)$![]() .
.
If $\nu _i\neq 0$![]() and $n_i\geq 2$
and $n_i\geq 2$![]() , taking $\nu _i=\nu _j$
, taking $\nu _i=\nu _j$![]() and $e_i=u$
and $e_i=u$![]() in (4.33), then we easily conclude that $g(K(u,\,u),\,u)=0$
in (4.33), then we easily conclude that $g(K(u,\,u),\,u)=0$![]() for any unit vector field $u\in \mathfrak {D} (\nu _i)$
for any unit vector field $u\in \mathfrak {D} (\nu _i)$![]() . Consequently, the assertion follows from the symmetry given in lemma 2.2.
. Consequently, the assertion follows from the symmetry given in lemma 2.2.
Claim 2. If $\nu ^2_i\neq \nu ^2_j$![]() , then $K(u,\,v)=0$
, then $K(u,\,v)=0$![]() for any $u,\,v\in \mathfrak {D} (\nu _i)\oplus \mathfrak {D}(\nu _j)$
for any $u,\,v\in \mathfrak {D} (\nu _i)\oplus \mathfrak {D}(\nu _j)$![]() .
.
If $\nu ^2_i\neq \nu ^2_j$![]() , it is obvious that $(\nu _i+\nu _j)(\nu _i-\nu _j)\neq 0$
, it is obvious that $(\nu _i+\nu _j)(\nu _i-\nu _j)\neq 0$![]() and we then obtain from (4.33) that $g(K(u,\,u),\,u)=0$
and we then obtain from (4.33) that $g(K(u,\,u),\,u)=0$![]() for any unit vector field $u\in \mathfrak {D}(\nu _i)$
for any unit vector field $u\in \mathfrak {D}(\nu _i)$![]() . From the result of the symmetry in lemma 2.2, we have $K(u,\,u)\notin \mathfrak {D}(\nu _i)$
. From the result of the symmetry in lemma 2.2, we have $K(u,\,u)\notin \mathfrak {D}(\nu _i)$![]() . Similarly, $g(K(v,\,v),\,v)=0$
. Similarly, $g(K(v,\,v),\,v)=0$![]() for any unit vector field $v\in \mathfrak {D}(\nu _j)$
for any unit vector field $v\in \mathfrak {D}(\nu _j)$![]() and thus $K(v,\,v)\notin \mathfrak {D}(\nu _j)$
and thus $K(v,\,v)\notin \mathfrak {D}(\nu _j)$![]() . Moreover, with the help of (4.34) and (4.36), it can be checked that $K(u,\,v)=0$
. Moreover, with the help of (4.34) and (4.36), it can be checked that $K(u,\,v)=0$![]() and $K(u,\,u)=K(v,\,v)\notin \mathfrak {D}(\nu _i)\oplus \mathfrak {D}(\nu _j)$
and $K(u,\,u)=K(v,\,v)\notin \mathfrak {D}(\nu _i)\oplus \mathfrak {D}(\nu _j)$![]() . When $r=2$
. When $r=2$![]() , claim 2 holds immediately. When $r\geq 3$
, claim 2 holds immediately. When $r\geq 3$![]() , for an arbitrary eigenvalue $\nu _k$
, for an arbitrary eigenvalue $\nu _k$![]() different from $\nu _i$
different from $\nu _i$![]() and $\nu _j$
and $\nu _j$![]() , it is known from $\nu ^2_i\neq \nu ^2_j$
, it is known from $\nu ^2_i\neq \nu ^2_j$![]() that either $\nu _i+\nu _k\neq 0$
that either $\nu _i+\nu _k\neq 0$![]() or $\nu _j+\nu _k\neq 0$
or $\nu _j+\nu _k\neq 0$![]() . In either case, we can apply (4.31) to obtain $K(u,\,u)=K(v,\,v)=0$
. In either case, we can apply (4.31) to obtain $K(u,\,u)=K(v,\,v)=0$![]() . Hence, claim 2 has been proved.
. Hence, claim 2 has been proved.
Claim 3. If $r\geq 2$![]() , there exist two distinct eigenvalues $\nu _i$
, there exist two distinct eigenvalues $\nu _i$![]() and $\nu _j$
and $\nu _j$![]() such that ${\nu _i+\nu _j=0}$
such that ${\nu _i+\nu _j=0}$![]() .
.
If $r\geq 2$![]() , we suppose on the contrary that $\nu _i+\nu _j\neq 0$
, we suppose on the contrary that $\nu _i+\nu _j\neq 0$![]() holds for any $\nu _i \neq \nu _j$
holds for any $\nu _i \neq \nu _j$![]() , namely $\nu ^2_i\neq \nu ^2_j$
, namely $\nu ^2_i\neq \nu ^2_j$![]() . It then follows from claim 2 that $K=0$
. It then follows from claim 2 that $K=0$![]() on $M^n$
on $M^n$![]() and hence $h=0$
and hence $h=0$![]() by definition. This together with the Gauss equation shows that $M^n$
by definition. This together with the Gauss equation shows that $M^n$![]() has constant sectional curvature, which is a contradiction to $r\geq 2$
has constant sectional curvature, which is a contradiction to $r\geq 2$![]() , and thus we have verified claim 3.
, and thus we have verified claim 3.
Now, according to claim 3, we denote by $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the two distinct eigenvalues of $P$
the two distinct eigenvalues of $P$![]() such that $\nu _1+\nu _2=0$
such that $\nu _1+\nu _2=0$![]() . In this situation, we further claim that $r\leq 2$
. In this situation, we further claim that $r\leq 2$![]() . Otherwise, if $r\geq 3$
. Otherwise, if $r\geq 3$![]() , then $(\nu _i+\nu _1)(\nu _i+\nu _2)\neq 0$
, then $(\nu _i+\nu _1)(\nu _i+\nu _2)\neq 0$![]() for an arbitrary eigenvalue $\nu _i$
for an arbitrary eigenvalue $\nu _i$![]() different from $\nu _1$
different from $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() . Therefore, it satisfies that $\nu ^2_i\neq \nu ^2_1$
. Therefore, it satisfies that $\nu ^2_i\neq \nu ^2_1$![]() and $\nu ^2_i\neq \nu ^2_2$
and $\nu ^2_i\neq \nu ^2_2$![]() , and so we obtain from claim 2 that:
, and so we obtain from claim 2 that:
Furthermore, we see that $K(u,\,v)=0$![]() in terms of the arbitrariness of $\nu _i$
in terms of the arbitrariness of $\nu _i$![]() , meaning that $h=0$
, meaning that $h=0$![]() identically. This contradiction implies that the number $r\le 2$
identically. This contradiction implies that the number $r\le 2$![]() .
.
Assume that $r=1$![]() . It is obvious that $M^n$
. It is obvious that $M^n$![]() has constant sectional curvature for $n\ge 3$
has constant sectional curvature for $n\ge 3$![]() .
.
Assume that $r=2$![]() . We will denote these two distinct eigenvalues of $P$
. We will denote these two distinct eigenvalues of $P$![]() by $\nu _1$
by $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() , whose multiplicities are $n_1$
, whose multiplicities are $n_1$![]() and $n_2$
and $n_2$![]() , respectively. Together with claim 3, it follows that $\nu _2=-\nu _1\neq 0$
, respectively. Together with claim 3, it follows that $\nu _2=-\nu _1\neq 0$![]() . In what follows, we shall argue by contradiction and suppose that $n_1\geq 2$
. In what follows, we shall argue by contradiction and suppose that $n_1\geq 2$![]() and $n_2\geq 2$
and $n_2\geq 2$![]() . Let $X^i_1,\,\ldots,\,X^i_{n_i}$
. Let $X^i_1,\,\ldots,\,X^i_{n_i}$![]() be the orthonormal eigenvector fields of $P$
be the orthonormal eigenvector fields of $P$![]() that span the distribution $\mathfrak {D}(\nu _i)$
that span the distribution $\mathfrak {D}(\nu _i)$![]() , $i=1,\,2$
, $i=1,\,2$![]() . Thus, we see from claim 1 and (4.36) that
. Thus, we see from claim 1 and (4.36) that
Since $M^n$![]() is minimal in $\mathbb {S}^{2n+1}$
is minimal in $\mathbb {S}^{2n+1}$![]() , by means of (4.38) we have
, by means of (4.38) we have

which implies that $g(K(u,\,u),\,v)=0$![]() for any $u\in \mathfrak {D}(\nu _1)$
for any $u\in \mathfrak {D}(\nu _1)$![]() and $v\in \mathfrak {D} (\nu _2)$
and $v\in \mathfrak {D} (\nu _2)$![]() . Similarly, there holds that $g(K(v,\,v),\,u)=0$
. Similarly, there holds that $g(K(v,\,v),\,u)=0$![]() and therefore $K(u,\,v)=0$
and therefore $K(u,\,v)=0$![]() . According to this and (4.38), we get $h=0$
. According to this and (4.38), we get $h=0$![]() identically, a contradiction to $r=2$
identically, a contradiction to $r=2$![]() . Hence, lemma 4.7 has been proved.
. Hence, lemma 4.7 has been proved.
Remark 4.8 By checking the proof of lemma 4.7 step by step, we see that the assertion still holds for $n=3$![]() , when the conformally flat condition is replaced by vanishing Weyl curvature tensor.
, when the conformally flat condition is replaced by vanishing Weyl curvature tensor.
4.4. Conformally flat minimal Legendrian submanifolds with $R\cdot Q=0$
In this subsection, assuming that $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() is a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
is a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() such that the Ricci tensor Ric is semi-parallel, by definition we have
such that the Ricci tensor Ric is semi-parallel, by definition we have

where $U,\,X,\,Y,\,Z$![]() are tangent vector fields on $M^n$
are tangent vector fields on $M^n$![]() . This implies that Ric is semi-parallel if and only if the Ricci operator $Q$
. This implies that Ric is semi-parallel if and only if the Ricci operator $Q$![]() is semi-parallel, i.e. $R\cdot Q=0$
is semi-parallel, i.e. $R\cdot Q=0$![]() .
.
Lemma 4.9 Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with $R\cdot Q=0$
with $R\cdot Q=0$![]() . Then, either $M^n$
. Then, either $M^n$![]() is of constant sectional curvature, or it is quasi-Einstein. In the latter case, the Schouten tensor of $M^n$
is of constant sectional curvature, or it is quasi-Einstein. In the latter case, the Schouten tensor of $M^n$![]() admits two distinct eigenvalues $\nu _1$
admits two distinct eigenvalues $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() at each point, where one of them is simple, such that $\nu _1+\nu _2=0$
at each point, where one of them is simple, such that $\nu _1+\nu _2=0$![]() .
.
Proof. Under the orthonormal frame $\{e_i\}^n_{i=1}$![]() on $M^n$
on $M^n$![]() as in § 4.2, direct calculations by using (2.29) yield that
as in § 4.2, direct calculations by using (2.29) yield that

where we used the relation $\mu _j-\mu _i=(n-2)(\nu _j-\nu _i)$![]() . Consequently, the number $r$
. Consequently, the number $r$![]() of distinct eigenvalues of the Schouten tensor $P$
of distinct eigenvalues of the Schouten tensor $P$![]() is at most $2$
is at most $2$![]() , and if $r=1$
, and if $r=1$![]() , then we conclude that $M^n$
, then we conclude that $M^n$![]() has constant sectional curvature.
has constant sectional curvature.
If $r=2$![]() , then we obtain from (4.41) that $\nu _1+\nu _2=0$
, then we obtain from (4.41) that $\nu _1+\nu _2=0$![]() by expressing the two distinct eigenvalues of $P$
by expressing the two distinct eigenvalues of $P$![]() by $\nu _1$
by $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() , respectively. Now, it suffices to prove that either of $\nu _1$
, respectively. Now, it suffices to prove that either of $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() must be simple. For this purpose, we shall suppose on the contrary that $n_i\geq 2$
must be simple. For this purpose, we shall suppose on the contrary that $n_i\geq 2$![]() , where $n_i$
, where $n_i$![]() is the multiplicity of $\nu _i$
is the multiplicity of $\nu _i$![]() for $i=1,\,2$
for $i=1,\,2$![]() . Let $\{X_i\}^{n_1}_{i=1}$
. Let $\{X_i\}^{n_1}_{i=1}$![]() (resp. $\{Y_j\}^{n_2}_{j=1}$
(resp. $\{Y_j\}^{n_2}_{j=1}$![]() ) be the orthonormal frame of $\mathfrak {D}(\nu _1)$
) be the orthonormal frame of $\mathfrak {D}(\nu _1)$![]() (resp. $\mathfrak {D}(\nu _2)$
(resp. $\mathfrak {D}(\nu _2)$![]() ). It then follows from lemma 4.6 (1) that
). It then follows from lemma 4.6 (1) that
Applying lemma 2.2 (1), we deduce from the Gauss equation (2.7) that
Since $M^n$![]() is conformally flat, it is easy to see from (2.29) that
is conformally flat, it is easy to see from (2.29) that
which together with (4.43) yields that
This contradicts with the fact $\nu _1+\nu _2=0$![]() , and thus lemma 4.9 has been proved.
, and thus lemma 4.9 has been proved.
4.5. Conformally flat Legendrian submanifolds with quasi-Einstein metric
In the following, according to lemmas 4.7 and 4.9, we shall deal with the case when $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() is a conformally flat Legendrian submanifold in $\mathbb {S}^{2n+1}$
is a conformally flat Legendrian submanifold in $\mathbb {S}^{2n+1}$![]() , such that it is quasi-Einstein with $\nu _1$
, such that it is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten tensor, and $\mathfrak {D}(\nu _1)$
the distinct eigenvalues of its Schouten tensor, and $\mathfrak {D}(\nu _1)$![]() and $\mathfrak {D}(\nu _2)$
and $\mathfrak {D}(\nu _2)$![]() the corresponding distributions of eigenspace, where $\nu _1+\nu _2=0$
the corresponding distributions of eigenspace, where $\nu _1+\nu _2=0$![]() and $\nu _1$
and $\nu _1$![]() is simple. Then, for a unit vector field $E_1$
is simple. Then, for a unit vector field $E_1$![]() of $\mathfrak {D}(\nu _1)$
of $\mathfrak {D}(\nu _1)$![]() and an orthonormal frame $\{E_i\}^n_{i=2}$
and an orthonormal frame $\{E_i\}^n_{i=2}$![]() of $\mathfrak {D}(\nu _2)$
of $\mathfrak {D}(\nu _2)$![]() , we see from (2.27) and (2.29) that
, we see from (2.27) and (2.29) that

where we used the facts tr $Q=n(n-1)\chi$![]() and $\nu _i={\mu _i}/{(n-2)}-{n\chi }/{(2(n-2))}$
and $\nu _i={\mu _i}/{(n-2)}-{n\chi }/{(2(n-2))}$![]() for $i=1,\,2$
for $i=1,\,2$![]() .
.
Lemma 4.10 Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Assume that $M^n$
. Assume that $M^n$![]() is quasi-Einstein with $\nu _1$
is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple. Then, it holds that
is simple. Then, it holds that

Proof. For any tangent vector $V$![]() on $M^n$
on $M^n$![]() , we denote by $V^\ell$
, we denote by $V^\ell$![]() the projection of $V$
the projection of $V$![]() onto $\mathfrak {D}(\nu _\ell )$
onto $\mathfrak {D}(\nu _\ell )$![]() for $\ell =1,\,2$
for $\ell =1,\,2$![]() , respectively. A straightforward computation shows that
, respectively. A straightforward computation shows that

where $2\leq i\leq n$![]() . As $M^n$
. As $M^n$![]() is conformally flat, we have $(\nabla _{E_1}P)E_i =(\nabla _{E_i}P)E_1$
is conformally flat, we have $(\nabla _{E_1}P)E_i =(\nabla _{E_i}P)E_1$![]() and then it follows that:
and then it follows that:
Multiplying the above equation with $E_1$![]() and further with $E_k$
and further with $E_k$![]() for $k\geq 2$
for $k\geq 2$![]() , we easily get:
, we easily get:
where $2\leq i,\,k\leq n$![]() . Similarly, we deduce from $(\nabla _{E_i}P)E_j=(\nabla _{E_j} P)E_i$
. Similarly, we deduce from $(\nabla _{E_i}P)E_j=(\nabla _{E_j} P)E_i$![]() that
that
where $2\leq i\neq j\leq n$![]() , and thus there holds
, and thus there holds
which together with the fact $\nu _1\neq \nu _2$![]() immediately yields that
immediately yields that
Next, with the help of $\nu _1\neq \nu _2$![]() , it is easy to see from (4.50) and (4.54) that
, it is easy to see from (4.50) and (4.54) that
On the contrary, by applying (4.51) we further have
Therefore, it can be checked from (4.46), (4.55) and (4.56) that

where we made use of the definition of the curvature tensor $R$![]() for $2\leq i\neq j \leq n$
for $2\leq i\neq j \leq n$![]() . Hence, $E_1(\alpha )=\alpha ^2$
. Hence, $E_1(\alpha )=\alpha ^2$![]() and $E_i(\alpha )=0$
and $E_i(\alpha )=0$![]() for $2\le i\le n$
for $2\le i\le n$![]() . This completes the proof of lemma 4.10.
. This completes the proof of lemma 4.10.
5. Proofs of the main results
In order to complete the proofs of the main results, we first verify the proposition:
Proposition 5.1 Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . Then, $M^n$
. Then, $M^n$![]() is quasi-Einstein with $\nu _1$
is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple, if and only if $(M^n,\,g)$
is simple, if and only if $(M^n,\,g)$![]() is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$
is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() , where $I\subset \mathbb {R}$
, where $I\subset \mathbb {R}$![]() , $g$
, $g$![]() is the induced metric on $M^n$
is the induced metric on $M^n$![]() and $(M_2,\,g_2)$
and $(M_2,\,g_2)$![]() has constant sectional curvature $c\ne 0$
has constant sectional curvature $c\ne 0$![]() .
.
Proof. First of all, omitting the upper index $i=1$![]() for $\lambda ^i_j$
for $\lambda ^i_j$![]() , by lemma 4.6 (2) we can write
, by lemma 4.6 (2) we can write
where $E_1$![]() is a unit vector field of $\mathfrak {D}(\nu _1)$
is a unit vector field of $\mathfrak {D}(\nu _1)$![]() and $\{E_j\}^n_{j=2}$
and $\{E_j\}^n_{j=2}$![]() is an orthonormal frame of $\mathfrak {D}(\nu _2)$
is an orthonormal frame of $\mathfrak {D}(\nu _2)$![]() . By means of the Gauss equation (2.7) and (4.46), it can be checked that:
. By means of the Gauss equation (2.7) and (4.46), it can be checked that:
Combining with the Codazzi equation for $K$![]() , we can apply (4.47) to calculate that:
, we can apply (4.47) to calculate that:

Consequently, $E_1(\lambda _2)=\alpha (2\lambda _2-\lambda _1)$![]() and $E_i(\lambda _1)=E_i (\lambda _2)=0$
and $E_i(\lambda _1)=E_i (\lambda _2)=0$![]() for all $i\ge 2$
for all $i\ge 2$![]() .
.
Secondly, noting from the minimality of $M^n$![]() that $0={\rm trace}\,K_{E_1}=\lambda _1 +(n-1)\lambda _2$
that $0={\rm trace}\,K_{E_1}=\lambda _1 +(n-1)\lambda _2$![]() , we solve from (5.2) to obtain that
, we solve from (5.2) to obtain that
where, replacing $E_1$![]() by $-E_1$
by $-E_1$![]() if necessary, we can always assume that $\lambda _1\geq 0$
if necessary, we can always assume that $\lambda _1\geq 0$![]() . Thus, $\alpha =0$
. Thus, $\alpha =0$![]() and it then follows from (4.47) that $\nu _1,\,\nu _2$
and it then follows from (4.47) that $\nu _1,\,\nu _2$![]() are constant and
are constant and
Therefore, $\mathfrak {D}(\nu _1)$![]() and $\mathfrak {D}(\nu _2)$
and $\mathfrak {D}(\nu _2)$![]() are both totally geodesic in $M^n$
are both totally geodesic in $M^n$![]() , and so $(M^n,\,g)$
, and so $(M^n,\,g)$![]() is locally a Riemannian product manifold $I\times M_2$
is locally a Riemannian product manifold $I\times M_2$![]() , where $I\subset \mathbb {R}$
, where $I\subset \mathbb {R}$![]() and $M_2$
and $M_2$![]() is the integral manifold of $\mathfrak {D}(\nu _2)$
is the integral manifold of $\mathfrak {D}(\nu _2)$![]() . Let $R_2$
. Let $R_2$![]() be the Riemannian curvature tensor of $M_2$
be the Riemannian curvature tensor of $M_2$![]() . Using (4.46), we easily get:
. Using (4.46), we easily get:
From this, we see that $(M_2,\,g_2)$![]() has constant sectional curvature $2\nu _2$
has constant sectional curvature $2\nu _2$![]() and $g_2$
and $g_2$![]() is the metric of $M_2$
is the metric of $M_2$![]() . As a result, $(M^n,\,g)$
. As a result, $(M^n,\,g)$![]() is locally isometric to the Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$
is locally isometric to the Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() , where $(M_2,\,g_2)$
, where $(M_2,\,g_2)$![]() has constant sectional curvature $c=2\nu _2\ne 0$
has constant sectional curvature $c=2\nu _2\ne 0$![]() .
.
Finally, if assuming that $(M^n,\,g)$![]() is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$
is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() , where $(M_2,\,g_2)$
, where $(M_2,\,g_2)$![]() has constant sectional curvature ${c\ne 0}$
has constant sectional curvature ${c\ne 0}$![]() , then
, then
where $E_1$![]() is a unit vector field tangent to $I$
is a unit vector field tangent to $I$![]() and $\{E_i\}^{n}_{i=2}$
and $\{E_i\}^{n}_{i=2}$![]() is an orthonormal frame on $M_2$
is an orthonormal frame on $M_2$![]() . Applying (5.7), we can verify the assertion by direct calculation.
. Applying (5.7), we can verify the assertion by direct calculation.
Now, by means of proposition 5.1 we are ready to prove the following theorem:
Theorem 5.2 (cf. theorem 1.9)
Let $M^n$![]() $(n\geq 3)$
$(n\geq 3)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() . If $(M^n,\,g)$
. If $(M^n,\,g)$![]() is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$
is locally isometric to a Riemannian product $I\times M_2=(I\times M_2,\,{\rm d}t^2\oplus g_2)$![]() , where $I\subset \mathbb {R}$
, where $I\subset \mathbb {R}$![]() , $g$
, $g$![]() is the induced metric on $M^n$
is the induced metric on $M^n$![]() and $(M_2,\,g_2)$
and $(M_2,\,g_2)$![]() has constant sectional curvature $c\ne 0$
has constant sectional curvature $c\ne 0$![]() , then $M^n$
, then $M^n$![]() is locally congruent to the Calabi torus.
is locally congruent to the Calabi torus.
Proof. According to theorem 2.5, it is known that $(M^n,\,g)$![]() is conformally flat for $n\ge 3$
is conformally flat for $n\ge 3$![]() , and therefore we obtain from proposition 5.1 that $M^n$
, and therefore we obtain from proposition 5.1 that $M^n$![]() is quasi-Einstein with $\nu _1$
is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple. Let $E_1\in \mathfrak {D}(\nu _1)$
is simple. Let $E_1\in \mathfrak {D}(\nu _1)$![]() be a unit vector field and $\{E_i\}^n_{i=2}$
be a unit vector field and $\{E_i\}^n_{i=2}$![]() an orthonormal frame of $\mathfrak {D}(\nu _2)$
an orthonormal frame of $\mathfrak {D}(\nu _2)$![]() . Here, $I\subset \mathbb {R}$
. Here, $I\subset \mathbb {R}$![]() and $M_2$
and $M_2$![]() are the integral manifolds of $\mathfrak {D}(\nu _1)$
are the integral manifolds of $\mathfrak {D}(\nu _1)$![]() and $\mathfrak {D}(\nu _2)$
and $\mathfrak {D}(\nu _2)$![]() , respectively. Related to the Schouten tensor $P$
, respectively. Related to the Schouten tensor $P$![]() of $M^n$
of $M^n$![]() , by calculation we have
, by calculation we have
Similar argument as in the proof of proposition 5.1 shows that

where $K^k_{ij}:=g(K(E_i,\,E_j),\,E_k)$![]() .
.
Next, we claim that $K^k_{ij}\equiv 0$![]() . To verify this, we argue by supposing on the contrary that there exists some point $x\in M^n$
. To verify this, we argue by supposing on the contrary that there exists some point $x\in M^n$![]() at which $K^k_{ij}\ne 0$
at which $K^k_{ij}\ne 0$![]() , and then divide the proof into the following four steps.
, and then divide the proof into the following four steps.
Step 1. There exists an orthonormal basis $\{Y_i\}^{n-1}_{i=1}$![]() of $T_xM_2$
of $T_xM_2$![]() such that the tensor $K$
such that the tensor $K$![]() of $M^n$
of $M^n$![]() takes the forms:
takes the forms:

where $X:=E_1(x)$![]() , $(n+1)-nc>0$
, $(n+1)-nc>0$![]() , and $2\le j\le n-1$
, and $2\le j\le n-1$![]() .
.
Since $K^k_{ij}(x)\ne 0$![]() for some point $x\in M^n$
for some point $x\in M^n$![]() , the symmetry of $K^k_{ij}$
, the symmetry of $K^k_{ij}$![]() in all indices implies that there exists a unit vector $Y_1\in U_xM_2:=\{v\in T_xM_2\,|\,g(v,\,v)=1\}$
in all indices implies that there exists a unit vector $Y_1\in U_xM_2:=\{v\in T_xM_2\,|\,g(v,\,v)=1\}$![]() , which is a compact set, such that the function $g(K(u,\,u),\,u)$
, which is a compact set, such that the function $g(K(u,\,u),\,u)$![]() defined on $U_xM_2$
defined on $U_xM_2$![]() attains an absolute maximum $\alpha _1:=g(K(Y_1,\,Y_1),\,Y_1)>0$
attains an absolute maximum $\alpha _1:=g(K(Y_1,\,Y_1),\,Y_1)>0$![]() and therefore $K(Y_1,\,Y_1)=-({1}/{\sqrt {n}})X +\alpha _1Y_1$
and therefore $K(Y_1,\,Y_1)=-({1}/{\sqrt {n}})X +\alpha _1Y_1$![]() . Then, a self-adjoint operator $\mathcal {A}(Y):T_xM_2\to T_xM_2$
. Then, a self-adjoint operator $\mathcal {A}(Y):T_xM_2\to T_xM_2$![]() can be defined by
can be defined by
It is obvious that $\mathcal {A}(Y_1)=\alpha _1Y_1$![]() . Choosing the unit eigenvectors $\{Y_j\}^{n-1}_{j=2}$
. Choosing the unit eigenvectors $\{Y_j\}^{n-1}_{j=2}$![]() of $\mathcal {A}$
of $\mathcal {A}$![]() orthogonal to $Y_1$
orthogonal to $Y_1$![]() satisfying $\mathcal {A}(Y_j) =\alpha _jY_j$
satisfying $\mathcal {A}(Y_j) =\alpha _jY_j$![]() , we can conclude from lemma 2.4 that $\alpha _1\ge 2\alpha _j$
, we can conclude from lemma 2.4 that $\alpha _1\ge 2\alpha _j$![]() , where $\alpha _j:=g(K(Y_1,\,Y_j),\,Y_j)$
, where $\alpha _j:=g(K(Y_1,\,Y_j),\,Y_j)$![]() . It then follows that
. It then follows that
Therefore, a straightforward calculation by using (2.7) and (2.29) shows that
which together with (5.8) immediately gives
On the contrary, by the minimality of $M^n$![]() we easily get:
we easily get:
This combining with (5.14) yields that
Consequently, noting the fact $\alpha _1\ge 2\alpha _j$![]() , we solve from (5.14) and (5.15) to obtain that
, we solve from (5.14) and (5.15) to obtain that

Hence, the assertion of step 1 follows immediately.
Step 2. There exists a vector field $\bar {V}_1$![]() on a neighbourhood $\bar {U}$
on a neighbourhood $\bar {U}$![]() of $x$
of $x$![]() such that the tensor $K$
such that the tensor $K$![]() of $M^n$
of $M^n$![]() takes the form:
takes the form:
where $\alpha _1$![]() is defined as in (5.17).
is defined as in (5.17).
Choose an arbitrary differentiable orthonormal frame $\{\bar {Y}\}^{n-1}_{i=1}$![]() on a neighbourhood $U$
on a neighbourhood $U$![]() of $x\in M^n$
of $x\in M^n$![]() such that $\bar {Y}_i(x)=Y_i$
such that $\bar {Y}_i(x)=Y_i$![]() , and define a mapping $\varphi :\mathbb {R}^{n-1}\times U\to \mathbb {R}^{n-1}$
, and define a mapping $\varphi :\mathbb {R}^{n-1}\times U\to \mathbb {R}^{n-1}$![]() by
by
where

are regarded as functions on $\mathbb {R}^{n-1}\times U:b_k=b_k(a_1,\,a_2,\,\ldots,\,a_{n-1},\,\tilde {x})$![]() . By means of (5.10), it is easy to see that $b_k(1,\,0,\,\ldots,\,0,\,x)=0$
. By means of (5.10), it is easy to see that $b_k(1,\,0,\,\ldots,\,0,\,x)=0$![]() for all $k$
for all $k$![]() , and
, and

This implies that $({\partial b_k}/{\partial a_j})$![]() is invertible at the point $(1,\,0,\,\ldots,\,0,\,x)\in \mathbb {R}^{n-1}\times U$
is invertible at the point $(1,\,0,\,\ldots,\,0,\,x)\in \mathbb {R}^{n-1}\times U$![]() . Consequently, by the implicit function theorem there exist differentiable functions $\{a_i(\tilde {x})\}_{1\leq i\leq n-1}$
. Consequently, by the implicit function theorem there exist differentiable functions $\{a_i(\tilde {x})\}_{1\leq i\leq n-1}$![]() which are defined on a neighbourhood $\bar {U}\subset U$
which are defined on a neighbourhood $\bar {U}\subset U$![]() of $x$
of $x$![]() and satisfy the relations:
and satisfy the relations:

Now, we put $\bar {V}_1=\sum ^{n-1}_{i=1}a_i\bar {Y}_i$![]() and thus $\bar {V}_1(x)=Y_1$
and thus $\bar {V}_1(x)=Y_1$![]() . Finally, we obtain (5.18) by applying (5.20) and (5.22). Hence, step 2 has been proved.
. Finally, we obtain (5.18) by applying (5.20) and (5.22). Hence, step 2 has been proved.
Step 3. There exists an orthonormal frame $\{\tilde {Y}_i\}^{n-1}_{i=1}$![]() on a neighbourhood $\tilde {U}\subset \bar {U}$
on a neighbourhood $\tilde {U}\subset \bar {U}$![]() of $x$
of $x$![]() such that the tensor $K$
such that the tensor $K$![]() of $M^n$
of $M^n$![]() takes the forms:
takes the forms:

where $(n+1)-nc>0$![]() and $2\le j\le n-1$
and $2\le j\le n-1$![]() .
.
For our purposes, we shall verify that the set
consists of finite numbers, which are independent of the point $x\in M^n$![]() . With the help of (5.10), we first find that $\Lambda _x$
. With the help of (5.10), we first find that $\Lambda _x$![]() is non-empty. Furthermore, for an arbitrary $\tilde {\alpha }_1$
is non-empty. Furthermore, for an arbitrary $\tilde {\alpha }_1$![]() associated with $V_1\in U_xM_2$
associated with $V_1\in U_xM_2$![]() satisfying $K(V_1,\, V_1)=-({1}/{\sqrt {n}})X+\tilde {\alpha }_1V_1$
satisfying $K(V_1,\, V_1)=-({1}/{\sqrt {n}})X+\tilde {\alpha }_1V_1$![]() , we can define another self-adjoint operator $\mathcal {B}(Y):T_xM_2\to T_xM_2$
, we can define another self-adjoint operator $\mathcal {B}(Y):T_xM_2\to T_xM_2$![]() by
by
where $X:=E_1(x)$![]() . As a result, $\mathcal {B}(V_1)=\tilde {\alpha }_1V_1$
. As a result, $\mathcal {B}(V_1)=\tilde {\alpha }_1V_1$![]() . Let $\{V_j\}^{n-1}_{j=2}$
. Let $\{V_j\}^{n-1}_{j=2}$![]() be the unit eigenvectors of $\mathcal {B}$
be the unit eigenvectors of $\mathcal {B}$![]() , orthogonal to $V_1$
, orthogonal to $V_1$![]() , with the corresponding eigenvalues $\{\tilde {\alpha }_j\}^{n-1}_{j=2}$
, with the corresponding eigenvalues $\{\tilde {\alpha }_j\}^{n-1}_{j=2}$![]() , respectively. Then
, respectively. Then
In this situation, applying (2.7) and (2.29), we easily get:
which combining with $(n+1)-nc>0$![]() implies that there exists an integer $0\le k\le n-2$
implies that there exists an integer $0\le k\le n-2$![]() such that, if necessary, after renumbering the basis, we have
such that, if necessary, after renumbering the basis, we have

As $0={\rm trace}\,K_{V_1}=\tilde {\alpha }_1+\tilde {\alpha }_2+\cdots +\tilde {\alpha }_{n-1}$![]() , it can be checked from (5.28) that
, it can be checked from (5.28) that

Hence, $\Lambda _x$![]() consists of finite numbers that are independent of the point $x\in M^n$
consists of finite numbers that are independent of the point $x\in M^n$![]() .
.
According to step 2, we see that $\|\bar {V}_1\|(x)=1$![]() for $\|\bar {V}_1\|:=\sqrt {g(\bar {V}_1,\, \bar {V}_1)}$
for $\|\bar {V}_1\|:=\sqrt {g(\bar {V}_1,\, \bar {V}_1)}$![]() . For this reason, there exists a neighbourhood $\tilde {U}\subset \bar {U}$
. For this reason, there exists a neighbourhood $\tilde {U}\subset \bar {U}$![]() of $x$
of $x$![]() so that $\bar {V}_1$
so that $\bar {V}_1$![]() does not vanish on $\tilde {U}$
does not vanish on $\tilde {U}$![]() . Thus, setting $\tilde {Y}_1=\bar {V}_1/\| \bar {V}_1\|$
. Thus, setting $\tilde {Y}_1=\bar {V}_1/\| \bar {V}_1\|$![]() , we derive from (5.18) that
, we derive from (5.18) that
where $\alpha _1$![]() is defined as in (5.17). As $\alpha _1/\|\bar {V}_1\|$
is defined as in (5.17). As $\alpha _1/\|\bar {V}_1\|$![]() changes continuously on $\tilde {U}$
changes continuously on $\tilde {U}$![]() , we conclude that $\|\bar {V}_1\|(\tilde {x})=\|\bar {V}_1\|(x)=1$
, we conclude that $\|\bar {V}_1\|(\tilde {x})=\|\bar {V}_1\|(x)=1$![]() for any $\tilde {x}\in \tilde {U}$
for any $\tilde {x}\in \tilde {U}$![]() , because $\Lambda _x$
, because $\Lambda _x$![]() consists of finite numbers. Similarly, after taking orthonormal vector fields $\tilde {Y}_2,\,\ldots,\,\tilde {Y}_{n-1}$
consists of finite numbers. Similarly, after taking orthonormal vector fields $\tilde {Y}_2,\,\ldots,\,\tilde {Y}_{n-1}$![]() orthogonal to $\tilde {Y}_1$
orthogonal to $\tilde {Y}_1$![]() such that $\{\tilde {Y}_i\}^{n-1}_{i=1}$
such that $\{\tilde {Y}_i\}^{n-1}_{i=1}$![]() forms an orthonormal frame on $\tilde {U}$
forms an orthonormal frame on $\tilde {U}$![]() , we follow the proof of step 1 to obtain (5.23) and finally complete the proof of step 3.
, we follow the proof of step 1 to obtain (5.23) and finally complete the proof of step 3.
Step 4. Show that $g(K(E_i,\,E_j),\,E_k)=K^k_{ij}\equiv 0$![]() for $2\le i,\,j,\,k\le n$
for $2\le i,\,j,\,k\le n$![]() .
.
Direct calculations by using (5.23) shows that

where $\alpha _1$![]() and $\alpha _2$
and $\alpha _2$![]() are defined as in (5.17) and $2\le j\le n-1$
are defined as in (5.17) and $2\le j\le n-1$![]() . Based on the relation
. Based on the relation
we deduce from (5.23) that $\nabla _{\tilde {Y}_1}\tilde {Y}_1=0$![]() and thus $(\nabla _{\tilde {Y}_1}K)(\tilde {Y}_j,\,\tilde {Y}_1)=0$
and thus $(\nabla _{\tilde {Y}_1}K)(\tilde {Y}_j,\,\tilde {Y}_1)=0$![]() for $2\le j\le n-1$
for $2\le j\le n-1$![]() . Together with the fact $\alpha _1-2\alpha _2\ne 0$
. Together with the fact $\alpha _1-2\alpha _2\ne 0$![]() , it is seen from (5.31) that $\nabla _{\tilde {Y}_j}\tilde {Y}_1=0$
, it is seen from (5.31) that $\nabla _{\tilde {Y}_j}\tilde {Y}_1=0$![]() for all $j\ge 2$
for all $j\ge 2$![]() . By the definition of the curvature tensor, we apply (4.46) and (5.8) to obtain that
. By the definition of the curvature tensor, we apply (4.46) and (5.8) to obtain that
This is a contradiction to $c\ne 0$![]() and hence we complete the proof of step 4.
and hence we complete the proof of step 4.
Now, for the orthonormal frame $\{E_i\}^n_{i=1}$![]() on $M^n$
on $M^n$![]() , from (5.9) it follows that
, from (5.9) it follows that

Consequently, by applying theorem 2.1 we conclude from (3.4) and (5.34) that $M^n$![]() is locally congruent to the Calabi torus.
is locally congruent to the Calabi torus.
5.1. Completion of the proof of theorem 1.3
$M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() . By means of lemma 4.7, we see that either $M^n$
. By means of lemma 4.7, we see that either $M^n$![]() is of constant sectional curvature, or it is quasi-Einstein with $\nu _1$
is of constant sectional curvature, or it is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple. In the former case, theorem 1.1 states that $M^n$
is simple. In the former case, theorem 1.1 states that $M^n$![]() is the totally geodesic sphere or the flat Clifford torus. In the latter case, according to proposition 5.1 and theorem 5.2, we conclude that $M^n$
is the totally geodesic sphere or the flat Clifford torus. In the latter case, according to proposition 5.1 and theorem 5.2, we conclude that $M^n$![]() is locally congruent to the Calabi torus. Conversely, these calculations in § 3 guarantee that examples (a)–(c) are all conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$
is locally congruent to the Calabi torus. Conversely, these calculations in § 3 guarantee that examples (a)–(c) are all conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() .
.
5.2. Completion of the proof of corollary 1.5
Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() . By means of lemma 4.1 and proposition 4.3, we calculate that
. By means of lemma 4.1 and proposition 4.3, we calculate that
Consequently, we have
by which we obtain (1.3) and find that the equality holds on $M^n$![]() if and only if the Weyl curvature tensor of $M^n$
if and only if the Weyl curvature tensor of $M^n$![]() vanishes identically. When $n\ge 4$
vanishes identically. When $n\ge 4$![]() , the assertion immediately follows from theorem 1.3 and proposition 3.1. When $n=3$
, the assertion immediately follows from theorem 1.3 and proposition 3.1. When $n=3$![]() , according to lemma 4.7 and remark 4.8, either $M^3$
, according to lemma 4.7 and remark 4.8, either $M^3$![]() has constant sectional curvature, or $M^3$
has constant sectional curvature, or $M^3$![]() is quasi-Einstein with $\nu _1$
is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator so that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator so that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple. In the former case, we obtain from theorem 1.1 that $M^3$
is simple. In the former case, we obtain from theorem 1.1 that $M^3$![]() is the totally geodesic sphere or the flat Clifford torus. In the latter case, by remark 4.8 and claim 1, we deduce from (4.34) and (4.36) that
is the totally geodesic sphere or the flat Clifford torus. In the latter case, by remark 4.8 and claim 1, we deduce from (4.34) and (4.36) that
where $E_1$![]() is a unit vector field of $\mathfrak {D}(\nu _1)$
is a unit vector field of $\mathfrak {D}(\nu _1)$![]() and $\{E_2,\,E_3\}$
and $\{E_2,\,E_3\}$![]() is an arbitrary orthonormal frame of $\mathfrak {D}(\nu _2)$
is an arbitrary orthonormal frame of $\mathfrak {D}(\nu _2)$![]() . As $M^3$
. As $M^3$![]() is minimal in $\mathbb {S}^7$
is minimal in $\mathbb {S}^7$![]() , we further have
, we further have

Therefore, similar calculations as in the proof of proposition 5.1 show that

Finally, combining with (3.4) and (5.39), we derive from theorem 2.1 that $M^n$![]() is locally congruent to the Calabi torus. Conversely, by § 3 these examples (a)–(c) for $n=3$
is locally congruent to the Calabi torus. Conversely, by § 3 these examples (a)–(c) for $n=3$![]() are all minimal Legendrian submanifolds in $\mathbb {S}^7$
are all minimal Legendrian submanifolds in $\mathbb {S}^7$![]() with semi-parallel tensor $K$
with semi-parallel tensor $K$![]() .
.
5.3. Completion of the proof of corollary 1.6
Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a closed minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a closed minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with vanishing Weyl curvature tensor. By calculation we apply (4.18) to obtain that
with vanishing Weyl curvature tensor. By calculation we apply (4.18) to obtain that
Now, by using the compactness of $M^n$![]() , we can integrate inequality (5.40) to obtain the integral inequality in (1.4), according to the divergence theorem, where the equality holds on $M^n$
, we can integrate inequality (5.40) to obtain the integral inequality in (1.4), according to the divergence theorem, where the equality holds on $M^n$![]() if and only if $M^n$
if and only if $M^n$![]() is of $C$
is of $C$![]() -parallel second fundamental form, i.e. $\bar \nabla ^\xi h=0$
-parallel second fundamental form, i.e. $\bar \nabla ^\xi h=0$![]() , which implies that $R\cdot K=0$
, which implies that $R\cdot K=0$![]() . When $n\ge 4$
. When $n\ge 4$![]() , the assertion follows from theorem 1.3 and proposition 3.1 immediately. When $n=3$
, the assertion follows from theorem 1.3 and proposition 3.1 immediately. When $n=3$![]() , Theorem 1.3 and (1.5) of Xing–Zhai [Reference Xing and Zhai33] state that $M^3$
, Theorem 1.3 and (1.5) of Xing–Zhai [Reference Xing and Zhai33] state that $M^3$![]() is locally congruent to one of the examples (a)–(c) for $n=3$
is locally congruent to one of the examples (a)–(c) for $n=3$![]() . Conversely, by § 3 the examples (a)–(c) for $n=3$
. Conversely, by § 3 the examples (a)–(c) for $n=3$![]() are closed minimal Legendrian submanifolds in $\mathbb {S}^7$
are closed minimal Legendrian submanifolds in $\mathbb {S}^7$![]() with $C$
with $C$![]() -parallel second fundamental form.
-parallel second fundamental form.
5.4. Completion of the proof of theorem 1.7
Let $M^n$![]() $(n\ge 3)$
$(n\ge 3)$![]() be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$
be a conformally flat minimal Legendrian submanifold in the unit sphere $\mathbb {S}^{2n+1}$![]() with semi-parallel Ricci tensor. Together with (4.40), it then follows from lemma 4.9 that either $M^n$
with semi-parallel Ricci tensor. Together with (4.40), it then follows from lemma 4.9 that either $M^n$![]() has constant sectional curvature, or $M^n$
has constant sectional curvature, or $M^n$![]() is quasi-Einstein with $\nu _1$
is quasi-Einstein with $\nu _1$![]() and $\nu _2$
and $\nu _2$![]() the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$
the distinct eigenvalues of its Schouten operator such that $\nu _1+\nu _2=0$![]() , where $\nu _1$
, where $\nu _1$![]() is simple. In the former case, either $M^n$
is simple. In the former case, either $M^n$![]() is the totally geodesic sphere, or $M^n$
is the totally geodesic sphere, or $M^n$![]() is the flat Clifford torus, in terms of theorem 1.1. In the latter case, applying proposition 5.1 and theorem 5.2, we derive that $M^n$
is the flat Clifford torus, in terms of theorem 1.1. In the latter case, applying proposition 5.1 and theorem 5.2, we derive that $M^n$![]() is locally congruent to the Calabi torus. Conversely, it is easy to see from proposition 3.1 that examples (a)–(c) are all conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$
is locally congruent to the Calabi torus. Conversely, it is easy to see from proposition 3.1 that examples (a)–(c) are all conformally flat minimal Legendrian submanifolds in $\mathbb {S}^{2n+1}$![]() with semi-parallel Ricci tensor.
with semi-parallel Ricci tensor.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Acknowledgements
This project was supported by Guangxi Science and Technology Program (Grant No. GuikeAD22035202), China Postdoctoral Science Foundation (Grant No. 2023M731810), National Natural Science Foundation of China (Grant Nos. 12171437 and 12201138), and Natural Science Foundation of Henan Province (Grant No. 242300420243).
Competing interests
None.