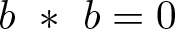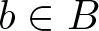1. Introduction
The Yang–Baxter equation (YBE) is a consistency equation that was independently set by Yang [Reference Yang18] and Baxter [Reference Baxter4] in the field of quantum statistical mechanics. The study of its solutions not only has many relevant interpretations in the realm of mathematical physics but it also plays a key role in the foundation of quantum groups and furnishes a multidisciplinary approach from a wide variety of areas such as Hopf algebras, knot theory, and braid theory among others (see [Reference Drinfel’d8, Reference Faddeev, Reshetikhin and Takhtajan10, Reference Gateva-Ivanova12]).
In the inspiring article of Drinfel’d [Reference Drinfel’d9], the attention is drawn to the so-called set-theoretical solutions of the YBE, a family of solutions that has been the object of a very prolific research since then. A (finite) set-theoretic solution of the YBE is a pair (X, r), where X is a (finite) set and 
$r\colon X \times X \rightarrow X \times X$ is a bijective map satisfying the equality 
$r_{12}r_{23}r_{12} = r_{23}r_{12}r_{23}$, where 
$r_{12} = r\times \operatorname{id}_X$ and 
$r_{23} = \operatorname{id}_X \times\, r$. The problem of classifying all set-theoretical solutions has brought to light the definitions of new algebraic structures so that properties of solutions can be translated in terms of such structures and vice-versa. In this light, left skew braces play a key role in the classification problem of non-degenerate solutions, i.e. set-theoretic solutions for which both components are bijective (see [Reference Guarnieri and Vendramin13] for example).
A (left) skew brace B is a set endowed with two group structures, 
$(B,+)$ and 
$(B,\cdot)$, satisfying the following skew distributivity property
\begin{equation*}a \cdot (b+c) = a\cdot b - a + a\cdot c\quad \forall\, a,b,c\in B.\end{equation*} If 
$(B,+)$ satisfies some property 
$\mathfrak{X}$ (such as abelianity), we say that B is a skew brace of 
$\mathfrak{X}$ type; in particular, skew braces of abelian type are just Rump’s (left) braces (see [Reference Guarnieri and Vendramin13] and [Reference Rump15]); note that both operations in B can be related by the so-called star product: 
$a \ \ast \ b = -a + a\cdot b -b$, for all 
$a,b\in B$. A non-degenerate set-theoretic solution of the YBE naturally leads to a skew brace structure over the group (see [Reference Rump15])
\begin{equation*}G(X,r) = \langle x \in X\,|\, xy = uv,\, \text{if}\ r(x,y) = (u,v)\rangle,\end{equation*} which is usually called the structure skew brace of (X, r). Conversely, every skew brace B defines a solution 
$(B,r_B)$ of the YBE (see [Reference Guarnieri and Vendramin13]).
Although it is very difficult to understand arbitrary non-degenerate set-theoretic solutions of the YBE, it turns out that nilpotency concepts for skew braces allows us to define certain particularly tamed classes of solutions. For example, right-nilpotent skew braces have been introduced to study the so-called multipermutation solutions, that is, non-degenerate set-theoretic solutions that can be retracted into the trivial solutions over a singleton after finitely many identification steps (see [Reference Cedó, Smoktunowicz and Vendramin7, Reference Gateva-Ivanova and Cameron11, Reference Jespers, Van Antwerpen and Vendramin14]); and it turns out that a non-degenerate set-theoretic solution is multipermutation if the structure skew brace associated with this solution is right-nilpotent and of nilpotent type (see [Reference Cedó, Smoktunowicz and Vendramin7], lemma 2.16 and [Reference Cedó, Jespers, Kubat, Van Antwerpen and Verwimp6], theorem 4.13). Thus, understanding if right-nilpotency is equivalent to some weaker concept could have a breakthrough effect on classifying the multipermutation solutions of the YBE, since it would mean we can recognize right-nilpotency with less computational effort. This is what led the authors of [Reference Cedó, Jespers, Kubat, Van Antwerpen and Verwimp6] to ask about the equivalence of right-nilpotency with the seemingly weaker concept of right-nil (see next section for the precise definitions).
Question 1.1. (see [Reference Cedó, Smoktunowicz and Vendramin7], Question 2.34)
• Let B be a finite right-nil skew brace. Is B right-nilpotent?
Another nilpotency concept that plays a major role in the theory of skew braces and the solutions of the YBE is that of central nilpotency. Central nilpotency is actually the strongest nilpotency concept for skew braces and was introduced by using a skew brace-theoretical analog of the centre of a group (see [Reference Bonatto and Jedlička5] and [Reference Jespers, Van Antwerpen and Vendramin14]), so it can be regarded as the true analog of the usual nilpotency for groups. As for right-nilpotency, it is relevant to understand if central nilpotency can be derived from the seemingly weaker concept of strong-nil.
Question 1.2. (see [Reference Cedó, Smoktunowicz and Vendramin7], Question 2.35)
• Let B be a finite strong-nil skew brace. Is B centrally nilpotent?
Our answers to both questions 1.1 and 1.2 are negative and in fact we provide an example of a finite brace B of order 32 that is strong-nil but not right-nilpotent (see example 2.5); keep in mind that strong-nil (resp. central nilpotency) implies right-nil (resp. right-nilpotency). In this example, it happens that 
$(b \ \ast \ b) \ \ast \ b=0=b \ \ast \ (b \ \ast \ b)$ for every 
$b\in B$ but 
$\operatorname{Soc}(B)=\{0\}$. Thus, the only special circumstance in which the above questions could be given a positive answer is that in which 
$b\ \ast \ b=0$ for all 
$b\in B$. This is in fact happening, as shown by our main result.
Main Theoremm 1.
Let B be a finite skew brace of nilpotent type such that 
$b \ \ast \ b=0$ for all 
$b\in B$. Then B is centrally nilpotent.
This result can also be considered as a partial extension of Smoktunowicz [Reference Smoktunowicz16], theorem 12. We further show that in our main theorem, the nilpotency of the additive group cannot be replaced by weaker concepts, such as that of supersoluble group (see example 2.4).
2. Preliminaries and results
Let 
$(B,+,\cdot)$ be a skew brace. The common identity element of both group operations is denoted by 0, and the product of two elements will be denoted by juxtaposition; as usual, group addition follows group product in the order of operations. A skew sub-brace of a skew brace is a subgroup of the additive group which is also a subgroup of the multiplicative group.
As we already noted in §1, both operations in B can be related by the so-called star product (
$a \ \ast \ b = -a + a\cdot b -b$, for all 
$a,b\in B$), which always comes first in the order of operations. Indeed, both group operations coincide if and only if 
$a \ \ast \ b=0$ for all 
$a,b\in B$; in this case, B is said to be a trivial skew brace. The following properties are essential to our work:
\begin{equation*}
\begin{array}{c}
(ab) \ \ast \ c = a \ \ast \ (b \ \ast \ c) + b \ \ast \ c + a \ \ast \ c,\\[0.2cm]
ab = a + a \ \ast \ b + b,\\[0.2cm]
a \ \ast \ (b+c) = a \ \ast \ b + b + a \ \ast \ c - b,
\end{array}\end{equation*} for all 
$a,b,c\in B$. If X and Y are subsets of B, then 
$X \ \ast \ Y$ is the subgroup of 
$(B,+)$ generated by the elements of the form 
$x \ \ast \ y$, for all 
$x \in X$ and 
$y \in Y$.
For every 
$a\in B$, the map 
$\lambda_a \colon B \rightarrow B,$ given by 
$\lambda_a(b) = -a + ab$, is an automorphism of 
$(B,+)$ and the map 
$\lambda\colon (B,\cdot) \rightarrow \operatorname{Aut}(B,+)$ which maps a to λa is a group homomorphism. For every 
$a,b\in B$,
\begin{equation*} a \ \ast \ b := \lambda_a(b) - b = - a + ab - b.\end{equation*} Left-ideals are λ-invariant skew sub-braces or equivalently skew sub-braces L such that 
$B \ \ast \ L \subseteq L$. A left-ideal S is said to be a strong left-ideal if 
$(S,+)$ is a normal subgroup of 
$(B,+)$, and an ideal if 
$(S,\cdot)$ is also a normal subgroup of 
$(B,\cdot)$, or equivalently 
$S \ \ast \ B \subseteq S$. Ideals of skew braces allow us to take quotients in a skew brace: if I is an ideal of B, then 
$B/I = \{bI = b+I: b \in B\}$ denotes the quotient of B over I. It should also be remarked that, for each skew sub-brace S and each strong left ideal I of B, we have 
$SI = S+I$. Furthermore, for the sake of simplicity, we introduce the following notations (here, E is a subset of B):
• To denote that C is a skew sub-brace of B, we write
$C\leqslant B$. To denote that I is an ideal of B, we write
$I\trianglelefteq B$.
If B is any skew brace, then the following subsets are always ideals of B:
\begin{equation*}
B \ \ast \ B,\quad\operatorname{Soc}(B) = \operatorname{Ker}(\lambda)\cap Z(B,+)\quad\text{and}\quad\zeta(B)=\operatorname{Soc}(B)\cap Z(B,\cdot),\end{equation*} where 
$Z(B,+)$ and 
$Z(B,\cdot)$ are the centres of 
$(B,+)$ and 
$(B,\cdot)$, respectively.
Now, we introduce the nilpotency concepts we deal with. Let B be a skew brace. Set 
$R_0(B)=B=L_0(B)$ and recursively define
\begin{equation*}R_{n+1}(B)=R_{n}(B) \ \ast \ B\quad\text{and}\quad L_{n+1}(B)=B \ \ast \ L_n(B)\end{equation*} for all 
$n\in\mathbb{N}$. Then B is right-nilpotent (resp. left-nilpotent) if 
$R_m(B)=\{0\}$ (resp. 
$L_m(B)=\{0\}$) for some 
$m\in\mathbb{N}$; the smallest such an m is the r-class (resp. l-class) of B. Thus, if B is right-nilpotent of r-class m, then
\begin{equation}
\begin{array}{c}
\underbrace{(\cdots((b \ \ast \ b) \ \ast \ \cdots ) \ \ast \ b)}_{m\;\text{times}}=0
\end{array}
\end{equation} for all 
$b\in B$; similarly, if B is left-nilpotent of l-class m, then
\begin{equation}
\begin{array}{c}
\underbrace{(b \ \ast \ (\cdots \ \ast \ (b \ \ast \ b))\cdots )}_{m\;\text{times}}=0
\end{array}
\end{equation} for all 
$b\in B$. Seemingly weaker concepts can be introduced if we only require (⋆) or (●) to hold (see [Reference Cedó, Smoktunowicz and Vendramin7] and [Reference Smoktunowicz16]). Thus, a skew brace is right-nil (resp. left-nil) if, for all 
$b\in B$, there is a suitable 
$m=m_b\in\mathbb{N}$ such that equation (⋆) (resp. (●)) holds.
In order to deal with right-nilpotency, we need the following chain of ideals of a skew brace B. Let 
$\operatorname{Soc}_0(B)=\{0\}$ and recursively define 
$\operatorname{Soc}_{n+1}(B)$ to satisfy the equality 
$\operatorname{Soc}_{n+1}(B)/\operatorname{Soc}_n(B)=\operatorname{Soc}\big(B/\operatorname{Soc}_n(B)\big)$. It has been proved in [Reference Cedó, Smoktunowicz and Vendramin7], lemma 2.16, that a skew brace B of nilpotent type is right-nilpotent if and only if 
$B=\operatorname{Soc}_n(B)$ for some 
$n\in\mathbb{N}$.
A stronger concept of nilpotency is given by central nilpotency. Let 
$\zeta_0(B)=\{0\}$ and recursively define 
$\zeta_{n+1}(B)$ to satisfy 
$\zeta_{n+1}(B)/\zeta_n(B)=\zeta\big(B/\zeta_n(B)\big)$. A skew brace is centrally nilpotent if there is some 
$m\in\mathbb{N}$ for which 
$B=\zeta_m(B)$. We refer to [Reference Ballester-Bolinches, Esteban-Romero, Ferrara, Perez-Calabuig and Trombetti3] for further information about centrally nilpotent skew braces. Here, we only observe that centrally nilpotent implies both left- and right-nilpotency, and that, conversely, left- and right-nilpotency imply central nilpotency if the skew brace is of nilpotent type (see corollary 2.15 of [Reference Jespers, Van Antwerpen and Vendramin14]).
Lemma 2.1.
Let B be a finite skew brace of nilpotent type such that 
$(B,\cdot)$ is nilpotent and 
$b \ \ast \ b=0$ for all 
$b\in B$. Then B is centrally nilpotent.
Proof. Let Lp be any Sylow p-subgroup of 
$(B,+)$ for some prime p. Since Lp is a characteristic subgroup of 
$(B,+)$ it follows that Lp is a left-ideal of B. Thus, Lp is also a Sylow p-subgroup of 
$(B,\cdot)$ and hence Lp is an ideal of B. It follows that 
$B=\operatorname{Dr}_{p\in\mathbb{P}}L_p$. Thus, in order to prove that B is centrally nilpotent, we may assume B has prime power order pn. Since the natural semidirect product 
$[(B,+)]_\lambda(B,\cdot)$ is a finite p-group, it follows that there is an element 
$a\in Z(B,+)$ such that 
$b \ \ast \ a=0$ for all 
$b\in B$. Now,
\begin{align*}
0&=(b+a) \; \ast \; (b+a)=(b\cdot a) \; \ast \; (b+a)=b \; \ast \; (a \; \ast \; (b+a))\\[0.2cm]
&\quad +a \; \ast \; (b+a)+b \; \ast \; (b+a)\\[0.2cm]
&=b \ \ast \ (a \ \ast \ b)+a \ \ast \ (b+a)+b \ \ast \ (b+a)=b \ \ast \ (a \ \ast \ b)+a \ \ast \ b
\end{align*} for all 
$b\in B$. By theorem 4.8 of [Reference Cedó, Smoktunowicz and Vendramin7], B is left-nilpotent. Let 
$c=a \ \ast \ b$. Then 
$b \ \ast \ c=-c$ and consequently 
$b \ \ast \ (-c)=c$. Therefore
\begin{equation*}\underbrace{b \ \ast \ \big(b \ \ast \ \cdots \ \ast \ (b}_{\ell\,\text{times}} \ \ast\, c)\big)=(-1)^\ell c\end{equation*} for every 
$\ell\in\mathbb{N}$, which means (by left-nilpotency) that 
$c=a \ \ast \ b=0$. Therefore 
$a\in\operatorname{Ker}(\lambda)$ and hence 
$a\in\operatorname{Soc}(B)$. By induction on the order of B, we have that 
$B=\operatorname{Soc}_m(B)$ for some 
$m\in\mathbb{N}$. Thus, lemma 2.16 of [Reference Cedó, Smoktunowicz and Vendramin7] shows that B is right-nilpotent. Since B is both left- and right-nilpotent, it is also centrally nilpotent by corollary 2.15 of [Reference Jespers, Van Antwerpen and Vendramin14].
Corollary 2.2.
Let B be a finite brace such that 
$b \ \ast \ b=0$ for all 
$b\in B$. Then B is centrally nilpotent.
Proof. It follows from theorem 12 of [Reference Smoktunowicz16] that B is left-nilpotent. Then theorem 4.8 of [Reference Cedó, Smoktunowicz and Vendramin7] shows that 
$(B,\cdot)$ is nilpotent. Finally, lemma 2.1 completes the proof.
Corollary 2.3.
Let B be a finite skew brace of prime power order such that 
$b \ \ast \ b=0$. Then B is centrally nilpotent.
Proof of the Main Theorem
For any prime p, let Lp be the Sylow p-subgroup of 
$(B,+)$. Since 
$(B,+)$ is nilpotent, it follows that 
$(B,+)$ is the direct product of its Sylow p-subgroups. By corollary 2.2, we may assume there is some prime p for which 
$(L_p,+)$ is non-abelian. Let 
$Z=Z(L_p,+)$. Now, Z × Q is a strong left-ideal of B, where Q is the Hall p ʹ-subgroup of 
$(B,+)$. By induction, Z × Q is centrally nilpotent, so, as a skew brace, it is the direct product of its additive Sylow subgroups (which are ideals), and in particular Z and Q are ideals of Z × Q.
Furthermore, Lp (which is also a strong left-ideal of B) is centrally nilpotent by corollary 2.3, and hence 
$\zeta(L_p)$ is a non-zero ideal of Lp contained in Z. Thus, 
$\zeta(L_p)$ is an ideal of Z × Q. Since Z × Q is centrally nilpotent, we have that
\begin{equation*}C=\zeta(L_p)\cap\zeta(Z\times Q)\neq\{0\}.\end{equation*} Let 
$c\in C$. Then 
$c\in Z(B,+)\cap Z(B,\cdot)$. Moreover, since any element of B can be written as a sum of an element of P and an element of Q, it follows that 
$c\in\operatorname{Ker}(\lambda)$. Therefore 
$c\in\zeta(B)$. By induction, 
$B/\langle c\rangle$ is centrally nilpotent, and so B is centrally nilpotent as well.
Example 2.4.
There exists a skew brace B of order 6 such that 
$b\ \ast \ b=0$ for all 
$b\in B$, but B is not right-nilpotent.
Proof. Let 
$(B,+)\simeq\operatorname{Sym}(3)$ and consider a product in B given by 
$ab = b+a$ for every 
$a,b\in B$. It turns out that 
$(B,+,\cdot)$ is a skew brace such that 
$a \ \ast \ a = 0$ for every 
$a \in B$. Moreover, 
$\lambda_a(b) = -a +b +a$ for every 
$a,b\in B$. Thus, 
$B \ \ast \ B = \langle c \rangle_+$ is the Sylow 3-subgroup of 
$(B,+)$. Since 
$B^{(3)} = (B \ \ast \ B) \ \ast \ B = B \ \ast \ B$, it follows that B is not right-nilpotent.
Example 2.5.
There exists a brace B of order 32 such that 
$(b \ \ast \ b) \ \ast \ b=0$ and 
$b \ \ast \ (b \ \ast \ b) = 0$ for all 
$b\in B$, but 
$\operatorname{Soc}(B)=\{0\}$, so, in particular, B is not right-nilpotent.
Proof. Let 
$(B,+) = \langle a \rangle \times \langle b \rangle \times \langle c \rangle \times \langle d \rangle \times \langle e\rangle$ and
\begin{align*}
(C, \cdot) = \Big\langle m_1,m_2,m_3,m_4,m_5 \Big|
\begin{array}{l}
m_i^2 = 1,\ 1\leq i \leq 5,\ (m_5m_2)^2 = (m_5m_3)^2 = 1,\\
m_5m_1m_5 = m_1m_3,\, m_5m_4m_5 = m_2m_4
\end{array}\Big\rangle
\end{align*} be groups of order 32 respectively isomorphic to 
$C_2 \times C_2 \times C_2\times C_2 \times C_2$ and to a semidirect product of the form 
$[C_2\times C_2 \times C_2\times C_2]C_2$. We have that C acts on B by means of the action 
$\lambda \colon C \rightarrow \operatorname{Aut}(B,+)$ defined by
\begin{align*}
\lambda_{m_1}(a) & = a, & \lambda_{m_2}(a) &= c+d+e, & \lambda_{m_3}(a) & = c+d+e, \\
\lambda_{m_1}(b) & = b, & \lambda_{m_2}(b) & = b, & \lambda_{m_3}(b) & = a+b+c+d+e,\\
\lambda_{m_1}(c) & = c, & \lambda_{m_2}(c) & = c, & \lambda_{m_3}(c) & = a+d+e, \\
\lambda_{m_1}(d) & = a+c+e, & \lambda_{m_2}(d) & = a+c+e, & \lambda_{m_3}(d) & = d,\\
\lambda_{m_1}(e) & = a+c+d, & \lambda_{m_2}(e) & = e , & \lambda_{m_3}(e) & = e,
\end{align*}
\begin{align*}
\lambda_{m_4}(a) & = a, & \lambda_{m_5}(a) & = a+b+c+e,\\
\lambda_{m_4}(b) & = b, & \lambda_{m_5}(b) & = a+b+c+d, \\
\lambda_{m_4}(c) & = a+d+e, & \lambda_{m_5}(c) & = a+d, \\
\lambda_{m_4}(d) & = a+c+e, & \lambda_{m_5}(d) & = a+b+e,\\
\lambda_{m_4}(e) & = e, & \lambda_{m_5}(e) & = e.
\end{align*} Consider the semidirect product 
$G = [B]C$ associated with this action (here, B is written multiplicatively for the sake of notation). Then G is trifactorized, as there exists 
$D = \langle abm_1, em_2, abdem_3, abcdem_4, bcm_5 \rangle \leqslant G$ such that 
$G = DC = BD$ and 
$C\cap D = B\cap D = \{1\}$. By [Reference Ballester-Bolinches and Esteban-Romero2, lemma 3.2], there exists a bijective 1-cocycle 
$\delta\colon C \rightarrow (B,+)$, with respect to λ, given by 
$D = \{\delta(c)c: c \in C\}$ (see table 1). This yields a product in B, provided by 
$bc = \delta(\delta^{-1}(b)\delta^{-1}(c))$ (see [Reference Ballester-Bolinches and Esteban-Romero2] for further details), and we obtain a brace 
$(B,+,\cdot)$ corresponding to SmallBrace(32, 24952) in the Yang–Baxter library [Reference Vendramin and Konovalov17] for GAP [1].
Table 1. Associated bijective 1-cocycle
Note that 
$\delta(x) \ \ast \ \delta(x) = 0$ for every 
$x\in C$ of order 2, while routine calculations show that for the rest of non-trivial elements 
$y\in B$, one has 
$y \ \ast \ y \neq 0$ but 
$(y \ \ast \ y) \ \ast \ y = y \ \ast \ (y \ \ast \ y) = 0$.
Now, every element of C can be written as 
$m_1^{\epsilon_1}m_2^{\epsilon_2}m_3^{\epsilon_3}m_4^{\epsilon_4}m_5^{\epsilon_5}$, with 
$\epsilon_i \in \{0,1\}$, for every 
$1\leq i \leq 5$. If 
$1\neq m_1^{\epsilon_1}m_2^{\epsilon_2}m_3^{\epsilon_3}m_4^{\epsilon_4}m_5^{\epsilon_5} \in \operatorname{Ker} \lambda$, then
\begin{equation*} \lambda_{m_1^{\epsilon_1}m_2^{\epsilon_2}m_3^{\epsilon_3}m_4^{\epsilon_4}m_5^{\epsilon_5}}(e) = e\end{equation*} and so 
$\epsilon_1 = 0$. Moreover, 
$\lambda_{m_2}$ fixes b and c, 
$\lambda_{m_3}$ fixes d, and 
$\lambda_{m_4}$ fixes a and b. Thus, 
$\operatorname{Ker}\lambda \cap \langle m_2,m_3,m_4\rangle =\{1\}$. Since 
$m_2m_5 = m_5m_2$, 
$m_3m_5 = m_5m_3$, and 
$m_4m_5 = m_5m_2m_4$, it is easy to check that also 
$\langle m_2,m_3,m_4,m_5 \rangle \cap \operatorname{Ker}(\lambda) = \{1\}$. Hence, 
$\operatorname{Ker} \lambda =\{1\}$ and 
$\operatorname{Soc}(B) =\{0\}$. Since 
$(B,+)$ is abelian, so B is not right-nilpotent.
Acknowledgements
We thank the referee for their careful reading of the manuscript and for pointing out a mistake in an earlier version of the proof of lemma 2.1.
Funding
All authors are members of the non-profit association ‘Advances in Group Theory and Applications’ (www.advgrouptheory.com). The second and fourth authors are supported by GNSAGA (INdAM). The second author has been supported by a research visiting grant issued by the Istituto Nazionale di Alta Matematica (INdAM). The fourth author is funded by the European Union—Next Generation EU, Missione 4 Componente 1 CUP B53D23009410006, PRIN 2022—2022PSTWLB—Group Theory and Applications.
