Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T20:08:46.546Z Has data issue: false hasContentIssue false
  • English
  • Français

XXI—The Evaluation of a Definite Integral Which Occurs in Asymptotic Partition Theory*

Published online by Cambridge University Press:  14 February 2012

M. M. Robertson
M. M. Robertson
Affiliation:
Department of Mathematics, University of Aberdeen.
Get access Rights & Permissions [Opens in a new window]

Synopsis

In order to estimate the number of partitions of a multi-partite number, the components of which are all large and of approximately the same order of magnitude, it is necessary to evaluate for ℛ(z1) > o(l=1, 2, …,j — 1) the integral

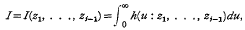
where

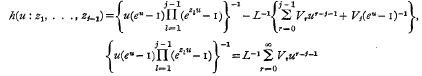
for o < u < 2π min (1, |z1|−1, …, |zj−1|−1) and 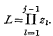Asymptotic expansions are obtained for I when the z1 are small. Simple expressions give an approximate value of I when every zl is real and exact formulæ are derived when every Zl is real and rational.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 65 , Issue 4 , 1961 , pp. 283 - 309
Copyright
Copyright © Royal Society of Edinburgh 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES TO LITERATURE

Knopp, K., 1928. Theory and Application of Infinite Series, 520–539. London and Glasgow.Google Scholar
Legendre, A. M., 1921. “Tables of the Logarithms of the Complete Γ-function to Twelve Figures”, Tracts for Computers, IV. Cambridge.Google Scholar
Whittaker, E. T., and Watson, G. N., 1920. Modern Analysis, 265–280. Cambridge.Google Scholar
Wright, E. M., 1958. “A Definite Integral in the Asymptotic Theory of Partitions”, Proc. Lond. Math. Soc., 8, 312–320.CrossRefGoogle Scholar