Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gutiérrez, Cristian E.
and
Wheeden, Richard L.
1991.
Sobolev interpolation inequalities with weights.
Transactions of the American Mathematical Society,
Vol. 323,
Issue. 1,
p.
263.
Chua, Seng-Kee
1994.
On weighted Sobolev interpolation inequalities.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 2,
p.
441.
Мазья, Владимир Гилелевич
Maz'ya, Vladimir Gilelevich
Шапошникова, Татьяна Олеговна
and
Shaposhnikova, Tat'yana Olegovna
2002.
Точечные интерполяционные неравенства для производных с наилучшими константами.
Функциональный анализ и его приложения,
Vol. 36,
Issue. 1,
p.
36.


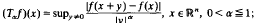 then, for certain weight functions
then, for certain weight functions 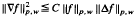 for large classes of weights.
for large classes of weights.