On Diophantine approximations of the solutions of q-functional equations
Published online by Cambridge University Press: 12 July 2007
Abstract
Given a sequence of linear forms
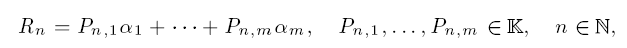 in m ≥ 2 complex or p-adic numbers α1, …,αm ∈ Kv with appropriate growth conditions, Nesterenko proved a lower bound for the dimension d of the vector space Kα1 + ··· + Kαm over K, when K = Q and v is the infinite place. We shall generalize Nesterenko's dimension estimate over number fields K with appropriate places v, if the lower bound condition for |Rn| is replaced by the determinant condition. For the q-series approximations also a linear independence measure is given for the d linearly independent numbers. As an application we prove that the initial values F(t), F(qt), …, F(qm−1t) of the linear homogeneous q-functional equation
in m ≥ 2 complex or p-adic numbers α1, …,αm ∈ Kv with appropriate growth conditions, Nesterenko proved a lower bound for the dimension d of the vector space Kα1 + ··· + Kαm over K, when K = Q and v is the infinite place. We shall generalize Nesterenko's dimension estimate over number fields K with appropriate places v, if the lower bound condition for |Rn| is replaced by the determinant condition. For the q-series approximations also a linear independence measure is given for the d linearly independent numbers. As an application we prove that the initial values F(t), F(qt), …, F(qm−1t) of the linear homogeneous q-functional equation
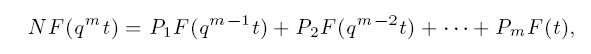 where N = N(q, t), Pi = Pi(q, t) ∈ K[q, t] (i = 1, …, m), generate a vector space of dimension d ≥ 2 over K under some conditions for the coefficient polynomials, the solution F(t) and t, q ∈ K*.
where N = N(q, t), Pi = Pi(q, t) ∈ K[q, t] (i = 1, …, m), generate a vector space of dimension d ≥ 2 over K under some conditions for the coefficient polynomials, the solution F(t) and t, q ∈ K*.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 3 , June 2002 , pp. 639 - 659
- Copyright
- Copyright © Royal Society of Edinburgh 2002
- 7
- Cited by


