Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T03:53:13.888Z Has data issue: false hasContentIssue false
  • English
  • Français

II.—On Certain Moduli of Rectangular Matrices

Published online by Cambridge University Press:  14 February 2012

C. R. Marathe
C. R. Marathe
Affiliation:
Muslim University, Aligarh, India
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper are considered certain numbers called moduli associated with a rectangular matrix with complex elements. These moduli have to satisfy a set of conditions analogous to those satisfied by the modulus of a complex number. For a complex rectangular matrix A = (aij) it is shown that R(A), C(A) and | A |° are moduli of A where:

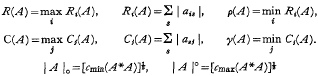
where cmin(H) and cmax(H) denote, respectively, the minimum and maximum characteristic values of the hermitian matrix H, A* being the transpose conjugate of A. Using the various properties of a modulus of a matrix and taking R(A), C(A) and | A |° as the moduli, a number of known results about the characteristic values of a matrix are obtained and extended. Relations between |A|°, |A |° R(A), p(A) and C(A), ɣ(A) are also studied. These relations provide a number of results about estimates of bounds of characteristic values of sums and products of matrices.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 65 , Issue 1 , 1958 , pp. 13 - 28
Copyright
Copyright © Royal Society of Edinburgh 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

Afriat, S. N., 1951. “Bounds for the characteristic values of matrix functions” Quart. J. Math., 2, 81–84.CrossRefGoogle Scholar
Browne, E. T., 1928. “The characteristic equation of a matrix”, Bull. Amer. Math. Soc., 34, 363–368.CrossRefGoogle Scholar
Farnell, A. B., 1944. “Limits for the characteristic roots of a matrix”, Bull. Amer. Math. Soc., 50, 789–794.CrossRefGoogle Scholar
Huff, G. B., 1955. “On quasi-idempotent matrices”, Amer. Math. Mon., 62, 334–339.CrossRefGoogle Scholar
Khan, N. A., 1956. “The characteristic roots of product of matrices”, Quart. J. Math., 7, 138–143.CrossRefGoogle Scholar
Ky Fan, and Hoffman, A. J., 1955. “Some metric inequalities in the space of matrices”, Proc. Amer. Math. Soc., 6, 111–116.CrossRefGoogle Scholar
Marathe, C. R., 1956. “A note on quasi-idempotent matrices”, Amer. Math. Mon. 63, 632–635.CrossRefGoogle Scholar
Nagy, , , Bela–s., 1956. “Remark on Roy's paper …”, Proc. Amer. Math. Soc., 7, 1.Google Scholar
Neumann, J. and , Goldstine, 1947. “Numerical inverting of matrices”, Bull. Amer. Math. Soc., 53, 1042–1044.Google Scholar
Parker, W. V., 1937. “The characteristic roots of a matrix”, Duke Math. J., 3, 484–487.CrossRefGoogle Scholar
Roy, S. N., 1954. “A useful theorem in the matrix theory”, Proc Amer. Math. Soc., 5, 635–638.CrossRefGoogle Scholar
Wong, Y. K., 1955. “Some properties of the proper values of a matrix”, Proc. Amer. Math. Soc., 6, 891–899.CrossRefGoogle Scholar