No CrossRef data available.
Article contents
A characterisation of tangential exceptional sets for 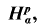 αp = n
αp = n
Published online by Cambridge University Press: 14 November 2011
Extract
In this paper we characterise some closed tangential exceptional sets for Hardy–Sobolev spaces  , αp = n, 1 < p ≦ 2, in terms of the annihilation of a nonisotropic Hausdorff measure.
, αp = n, 1 < p ≦ 2, in terms of the annihilation of a nonisotropic Hausdorff measure.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 3 , 1996 , pp. 625 - 641
- Copyright
- Copyright © Royal Society of Edinburgh 1996
References
1Ahern, P. and Bruna, J.. On holomorphic functions in the ball with absolutely continuous boundary values. Duke Math. J. 58 (1988), 129–41.Google Scholar
2Ahern, P. and Cohn, W.. Exceptional sets for Hardy-Sobolev functions, p> 1. Indiana Univ. Math.J. 38 (1989), 417–51.CrossRefGoogle Scholar
3Ahern, P. and Nagel, A.. Strong Lp-estimates for maximal functions with respect to singular measures with applications to exceptional sets. Duke Math. J. 53 (1986), 359–93.CrossRefGoogle Scholar
4Beatrous, F.. Estimates for derivatives of holomorphic functions in pseudoconvex domains. Math. Z. 191 (1986), 91–116.CrossRefGoogle Scholar
5Beatrous, F. and Burbea, J.. Sobolev spaces of holomorphic functions in the ball. Dissertationes Math. 256(1989), 1–57.Google Scholar
6Cascante, C. and Ortega, J. M.. Tangential-exceptional sets for Hardy–Sobolev spaces. Illinois J. Math. 39 (1995), 68–17.CrossRefGoogle Scholar
7Cifuentes, P., Dorronsoro, J. R. and Sueiro, J.. Boundary tangential convergence on spaces of homogeneous type. Trans. Amer. Math. Soc. 332 (1992), 331–50.CrossRefGoogle Scholar
8Cohn, W.. Non-isotropic Hausdorff measure and exceptional sets for holomorphic Sobolev functions. Illinois J. Math. 33 (1989), 673–90.CrossRefGoogle Scholar
9Dorronsoro, J. R.. Poisson integrals of regular functions. Trans. Amer. Math. Soc. 297 (1986), 669–85.CrossRefGoogle Scholar
10Hansson, K.. Imbedding theorems of Sobolev type in potential theory. Math. Scand. 45 (1979), 77–102.CrossRefGoogle Scholar
11Nagel, A., Rudin, W. and Shapiro, J.. Tangential boundary behavior of functions in Dirichlet-type spaces. Ann. of Math. 116 (1982), 331–60.CrossRefGoogle Scholar
13Shaw, K.. Tangential limits and exceptional sets for holomorphic Beson functions in the unit ball of Cn. Illinois J. Math. 37 (1993), 171–85.CrossRefGoogle Scholar
14Sueiro, J.. Tangential boundary limits and exceptional sets for holomorphic functions in Dirichlettype spaces. Math. Anal. 286 (1990), 661–78.CrossRefGoogle Scholar


