Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T16:15:17.336Z Has data issue: false hasContentIssue false
  • English
  • Français

19.—Improved Boundedness Conditions for Lowndes' Operators*

Published online by Cambridge University Press:  14 February 2012

Philip Heywood
Philip Heywood
Affiliation:
Department of Mathematics, University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Synopsis

The operator Ik(η, α) and its adjoint Kk(η, α) have obvious boundedness properties for α ≧½ because of their resemblance to fractional integrals. By expressing Ik(0, α) as the product of two Hankel transformations and a translation Heywood and Rooney [1] have shown that if 0<α<½ then Ik(η, α) and Kk(η, α) can be extended to bounded operators from a weighted Lp space to itself provided that 2/(1+α) ≦ p ≦ 2/(1−α) and the weight is suitably restricted. Heywood and Rooney conjectured that this p range could be improved, andin the present paper it is extended to

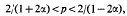
which may be best possible.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 73 , 1975 , pp. 291 - 299
Copyright
Copyright © Royal Society of Edinburgh 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Heywood, P. and Rooney, P. G., On the boundedness of Lowndes' operators. J.London Math. Soc, 10, 241–248, 1975.CrossRefGoogle Scholar
2Lowndes, J. S., A generalisation of the Erdé;lyi-Kober operators. Proc. Edinburgh Math. Soc, 17, 139–148, 1970.CrossRefGoogle Scholar
3Rooney, P. G., On the ranges of certain fractional integrals. Canad. J. Math., 24, 1198–1216, 1972.CrossRefGoogle Scholar
4Rooney, P. G., A technique for studying the boundedness and extendability of certain types of operators. Canad. J. Math., 25, 1090–1102, 1973.CrossRefGoogle Scholar