This paper studies Sobolev spaces under perturbation of domains of definition. It establishes the basic concepts, methods and results for the convergence of sequences of sets in ℝn, the strong and weak convergence of sequences of Sobolev spaces, the discrete compactness of natural embeddings and the continuous convergence of continuous linear functionals, boundary integrals and trace operators for sequences of Sobolev spaces.

A generalisation is considered of the potential barrier problem beyond the familiar case in which the barrier is bounded by transition points of order one. Here, the two transition points involved are of arbitrary odd order. The approximate method employed, though formal in character, avoids certain pitfalls often made in the past whereby certain exponentially small terms within the barrier are confounded with inherent error terms. This confusion is avoided in the treatment given here by tracing uniformly approximate solutions round the transition points in the complex plane by means of the Stokes phenomenon, the method not requiring the dubious concept of a subdominant term existing in the presence of a dominant term on a Stokes line. At the same time, the solutions to which the reflection and transmission coefficients may be attached are carefully discussed, so that the appearance of a small exponential term may be seen to be genuine when taken in conjunction with inherent error terms. The resulting formula for the modulus of the reflection coefficient generalizes the more elementary formula.

An analogue of the Riemannian theory of uniqueness of Fourier coefficients is developed for Sturm Liouville series, using asymptotic formulae for the eigenfunctions and other quantities. This theory generalises earlier work by Haar in that the coefficient function in the differential equation is only assumed to be integrable.

Integral inequalities are used to obtain comparison theorems for a class of second-order differential equations which includes the Emden-Fowler equation, certain Liénard equations, and linear equations of the form d2y/dx2+f(x)y = 0. For these linear equations the results below imply Sturm's classical comparison theorem.

In this article we examine the qualitative behaviour of non-planar equilibrium states ofnon-linearly elastic rods subject to terminal loads. In our geometrically exact theory, a rod is endowed with enough geometric structure for it to undergo flexure, torsion, axial extension, and shear. The constitutive equations give appropriate stress resultants and couples as non-linear functions of appropriate strains. These constitutive relations must meet minimal conditions ensuring that they be physically reasonable. It turns out that the equilibrium states of such a rod are governed by a boundary value problem for a quasilinear fifteenth-order system of ordinary differential equations.

This paper examines the mathematical problem of the propagation of a smooth fronted wavein the context of shallow water theory. Here, a smooth fronted wave will be taken to be one in which the surface slope is continuous across a line in the free-surface, while the second derivative of the surface slope is discontinuous across that same line. This discontinuity line in the surface then plays the role of the wavefront. After establishing that such wavefronts propagate along the characteristics, and deriving the appropriate transport equations, the explicit form is found for the acceleration with respect to distance of the horizontal component of the water velocity of the surface immediately behind the wavefront as a function of position and seabed profile when the wave propagates into still water. The result is then used to prove that in this approximation such a wave cannever break immediately behind the wavefront before the shore line is reached.

In this paper we consider the problem of defining a convolution, analogous to the classical convolution of scalar measures, of measures defined on the Borel sets of a locally compact semi-group S and having values in a Banach algebra . Using the bilinearintegral introduced by Bartle we show that the formalism of the scalar case persists in situations of considerable generality so that the formula

suitably interpreted, gives a Banach algebra structure to a large class of valued measures defined on S. Themethods exploit the connection between vector measures and operators and involve some results of independent interest.

The first part of this paper is devoted to a study of the classical bifurcation problem in a Hilbert space, under the assumption that the operators involved are gradient operators, but not necessarily compact. Our approach to the problem was introduced by Krasnosel'skii, but here we show that his assumption about the compactness of the operators can be replaced by a much weaker Lipschitz type condition, without affecting the generality of his conclusions.

The rest of the paper is concerned with the analogous problem when the operator is knownto be asymptotically linear rather than Fréchet differentiable. Indeed, we show that this question can always be reduced to the first case, after some manipulation. After this manipulation the new operator is found to be a Fréchet differentiable gradient operator, and so we can invoke the results of the first part. This manipulation is in the spirit of that of [11] but is necessarily different.

The two basic problems solved here are (1) a disc charged to a uniform potential placed between two earthed planes parallel to its plane, each a small distance h from the disc, (2) the space filled with viscous fluid and the disc slowly rotating uniformly about its axis with the planes held at rest. The total charge or turning moment are calculated as series in powers of h, giving four terms in each case. An approximate method devised by Maxwell [5] is shown to have three terms correct in both cases.

We use programmes for the Todd-Coxeter coset enumeration algorithm and the modified Todd-Coxeter coset enumeration algorithm to investigate a class of generalised Fibonacci groups. In particular we use these techniques to discover a finite non-metacyclic Fibonacci group and to study its structure.

Conditions are obtained which ensure that a 2nth order ordinary differential equation on a halfaxis have at most n linearly independent square-integrable solutions. The emphasis is on bounds on the integrals of the coefficients, and on conditions imposed over a sequence of intervals.

Two eigenvalue problems associated with steady rotations of a chain are considered. To compare the spectra of these two problems, let σK(n) denote the set of all angular velocities with which a chain of unit length with one end fixed and the other free can rotate in a vertical plane so as to have exactly n nodes on thevertical axis (including the fixed end). In a linearised theory σK(n) is a single point, i.e.

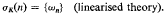
In the full non-linear theory σK(n) is an infinite interval lying to the right of ⍵n. Indeed,

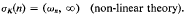
This is established in [1].

Next, let σM(β, n) denote the set of all angular velocities with which a chain, having ends fixed at unit distance apart on the vertical axis, can rotate in a vertical plane so as to have exactly n+l nodes on the vertical axis (including the ends) and so that the tension takes the value β at the lower end. This problem, in which the length of the chain is not prescribed is a model for a spinning process in which the ‘chain’ is continuously created in a rotating configuration. For β>0, we again have in the linearised theory that σM(β, n) is a singleton, i.e.

In the full non-linear theory σM(β, n) lies to the left of λn(β). Although unable to determine exactly σM(β, n) for β>0, we have

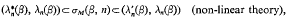
where ⍵n λn(β), 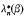and 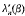are all characterised as the nth zeros of known combinations of Bessel functions.

The propagation of sound from a point source placed in a subsonic jet separated by two plane vortex sheets from two semi-infinite still media is considered and it is found that instability waves arise at particular points on the vortex sheets and that their effect is confined to certain regions.

Let X be the boundary of a compact set which does not separate the plane, C. Let Φ and Ψ be homeomorphisms of C to C with opposite orientations. Then every continuous complex-valued function on X is the uniform limit on X of sums p(Φ)+q(ψ), where p and q are analytic polynomials.

The present paper is concerned with the problem of regularity of weak solutions of boundary value problems. We shall present a new method to prove differentiability on the boundary. This method was developed in our thesis [12] within the theory of abstract Sobolev spaces, introduced by Stummel [14]. Here, we shall describe it by applying it to elliptic boundary value problems. It will be seen that the advantage of this method consists in the fact that it is based on functional analysis only and therefore may be used for other types of differential equations as well.

This paper is concerned with solutions of the ordinary differential equation

where ℒ is a real formally self-adjoint, linear differential expression of order 2n, and the perturbed term f satisfies

for some σ∈[0, 1]. Here λ(·) is locally integrable on [0,∞).

In particular it is shown, under circumstances detailed in the text, that (*) possesses solutions in the Hilbert function space L2(0,∞).

An analogue of full-range Fourier series is introduced in the Sturm-Liouville setting and a theorem generalising Wiener's theorem for functions with absolutely convergent Fourier series is proved. The Banach algebra structure of the theory is examined. Use is made of second-order asymptotic formulae for the Sturm-Liouville eigenfunctions.

New proofs are given for some main results in the theory of linear-quadratic optimal control.

The operator Ik(η, α) and its adjoint Kk(η, α) have obvious boundedness properties for α ≧½ because of their resemblance to fractional integrals. By expressing Ik(0, α) as the product of two Hankel transformations and a translation Heywood and Rooney [1] have shown that if 0<α<½ then Ik(η, α) and Kk(η, α) can be extended to bounded operators from a weighted Lp space to itself provided that 2/(1+α) ≦ p ≦ 2/(1−α) and the weight is suitably restricted. Heywood and Rooney conjectured that this p range could be improved, andin the present paper it is extended to

which may be best possible.

Given a symmetric (formally self-adjoint) ordinary linear differential expression L which is regular on the interval [0, ∞) and has C∞ coefficients, we investigate the relationship between the deficiency indices of L and those of p(L), where p(x) is any real polynomial of degree k > 1. Previously we established the following inequalities: (a) For k even, say k = 2r, N+(p(L)), N−(p(L)) ≧ r[N+(L)+N−(L)] and (b) for k odd, say k = 2r+1

where N+(M), N−(M) denote the deficiency indices of the symmetric expression M (or of the minimal operator associated with M in the Hilbert space L2(0, ∞)) corresponding to the upper and lower half-planes, respectively. Here we give a necessary and sufficient condition for equality to hold in the above inequalities.