Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-07T02:20:09.239Z Has data issue: false hasContentIssue false
  • English
  • Français

7.—Convolution of Vector Measures*

Published online by Cambridge University Press:  14 February 2012

A. J. White
A. J. White
Affiliation:
Department of Mathematics, University of Aberdeen
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we consider the problem of defining a convolution, analogous to the classical convolution of scalar measures, of measures defined on the Borel sets of a locally compact semi-group S and having values in a Banach algebra 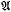. Using the bilinearintegral introduced by Bartle we show that the formalism of the scalar case persists in situations of considerable generality so that the formula

suitably interpreted, gives a Banach algebra structure to a large class of 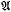valued measures defined on S. Themethods exploit the connection between vector measures and operators and involve some results of independent interest.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 73 , 1975 , pp. 117 - 135
Copyright
Copyright © Royal Society of Edinburgh 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bartle, R. G., A general bilinear vector integral. Stadia Math., 15, 337–352, 1956.CrossRefGoogle Scholar
2Batt, J. and Berg, E. J., Linear bounded transformations on the space of continuous functions. J. Functional Analysis, 4, 215–239, 1969.CrossRefGoogle Scholar
3Berberian, S. K., Measure and integration. New York: Macmillan, 1965.Google Scholar
4Chow, P. S., On some Banach algebras of measures (Ph.D. Thesis). Aberdeen Univ., 1969.Google Scholar
5Duchon, M., A convolution algebra of vector-valued measures on a compact Abelian semigroup. Rev. Roumaine Math. Pures Appl., 16, 1467–1476, 1971.Google Scholar
6Dinculeanu, N., Integral representation of dominated operations on spaces of continuous vector fields. Math. Ann., 173, 147–180, 1967.CrossRefGoogle Scholar
7Dobrakov, I., On integration in Banach spaces, I. Czechoslovak Math. J., 20, 511–536, 1970.CrossRefGoogle Scholar
8De Leeuw, K., The Fubini theorem and convolution formula for regular measures. Math. Scand., 11, 117–122, 1962.CrossRefGoogle Scholar
9Dunford, N. and Schwartz, J., Linear operators, I. New York: Interscience, 1958.Google Scholar
10Eberlein, W. F., Abstract ergodic theorems and weak almost-periodic functions. Trans. Amer. Math. Soc, 67, 217–240, 1947.CrossRefGoogle Scholar
11Glicksberg, I., Weak compactness and separate continuity. Pacific J. Math., 11, 205–214, 1961.CrossRefGoogle Scholar
12Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires. Mem. Amer. Math. Soc, 16, 1965.Google Scholar
13Halmos, P. R., Measure theory. New York: Van Nostrand, 1950.CrossRefGoogle Scholar
14Heinich, H., Convolution des mesures vectorielles. C.R. Acad. Sci. Paris, 271A, 159–161, 1970.Google Scholar
15Hewitt, E. and Ross, K. A., Abstract harmonic analysis, I. Berlin: Springer, 1963.Google Scholar
16Johnson, B. E., Separate continuity and measurability. Proc. Amer. Math. Soc, 20, 420–422, 1969.CrossRefGoogle Scholar
17Pym, J., The convolution of functional on spaces of bounded functions. Proc. London Math. Soc, 15, 84–104, 1965.Google Scholar