§ 1 Introduction. The formulae
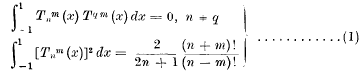
where n, q, m are positive integers, are well known. I am not aware, however, of any paper dealing with the corresponding definite integrals of products of two Ferrers' Associated Legendre Functions of different integral orders and degrees. With the help of the formulae given in my previous paper in this volume it is possible to discuss these integrals. I have found in the case of the first integral that if the orders of the two associated functions are both odd or both even and if, in each case, the degrees are both odd or both even or equal, the integral has usually a non-zero value. If, however, the orders are both odd or both even and if the degree of the function having the greater order is less than that of the other, or if the degrees are one odd and one even, the integral vanishes. Further, if one of the orders be odd and the other even, and the corresponding degrees are also even and odd (or odd and even), the integral has a non-zero value; in all other cases it vanishes. The values of the second integral can be obtained in a similar manner. An example of the methods employed and the results obtained is given in the following section.