No CrossRef data available.
Let umn, vmn be functions of m and n, vmn being real and positive for all positive values of m and n. Suppose that either vmn increases steadily to infinity with n, or that umn both tend to zero (the latter steadily) as n → ∞, for any fixed value of m. Denote 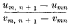 by wmn, and assume that
by wmn, and assume that 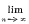 wmn exists for every value of m, being denoted by lm. Then from Stolz' extension of a result proved by Cauchy, and an allied theorem, we have
wmn exists for every value of m, being denoted by lm. Then from Stolz' extension of a result proved by Cauchy, and an allied theorem, we have 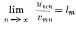 , for all values of m. It follows from Pringsheim's Theorem that if the double limit of
, for all values of m. It follows from Pringsheim's Theorem that if the double limit of 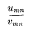 exists, being l, then lm → l as m → ∞.
exists, being l, then lm → l as m → ∞.
1 Or for all values of m and n greater than fixed values, say m 1 and n 1.
2 See Bromwich Infinite Series, pp. 377–378, for both of these.
3 Hereafter when the word “monotonic” is used, the functions concerned are to be regarded as real.