No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
The following is a direct proof of a theorem by Zia-ud-Din.
Let {ν} ≡ {ν1, ν2, …, νp)} be any S-function of weight r + s such that
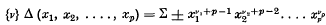
in the alternant denoted in the theorem by A(αβγ….). Let {μ} be an S-function of weight s, equal to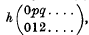 
and let {λ} be an S-function of weight r, such that {λ}δ(x1, …,xp) is obtained with coefficient gλμν by diminishing the indices in the alternant {ν}δ(x1, …,xp) according to the theorem.
page 261 note 1Proc. Edinburgh Math. Soc., 4 (1934), 51.Google Scholar
page 261 note 2Littlewood, D. E. and Richardson, A. R., Phil. Trans. Roy. Soc. (A), 233 (1934), 99.CrossRefGoogle Scholar
You have
Access