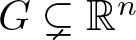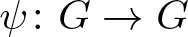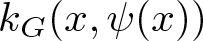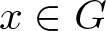1. Introduction and main results
1.1. Background
Let ![]() $G\subsetneq \mathbb{R}^n$ (
$G\subsetneq \mathbb{R}^n$ (![]() $n\geq 2$) be a domain, where the closure
$n\geq 2$) be a domain, where the closure ![]() $\overline{G}$ and the boundary
$\overline{G}$ and the boundary ![]() $\partial G$ of G are taken in the topology of the Riemann sphere
$\partial G$ of G are taken in the topology of the Riemann sphere ![]() $\mathbb{\overline{R}}^n=\mathbb{R}^n\cup\{\infty\}$. We define
$\mathbb{\overline{R}}^n=\mathbb{R}^n\cup\{\infty\}$. We define
 \begin{align*}
\mathcal{T}_H(G) & := \big \{\psi:\, \overline{G} \rightarrow \overline{G}\;\big |\; \psi\; \mbox{is a homeomorphism such that}\\
& \quad \mbox{the restriction }\;\psi|_G\; \mbox{is} \ H \mbox{-}{QC \ and}\;\psi|_{\partial G}={\text{id}}_{\partial G}\big \},
\end{align*}
\begin{align*}
\mathcal{T}_H(G) & := \big \{\psi:\, \overline{G} \rightarrow \overline{G}\;\big |\; \psi\; \mbox{is a homeomorphism such that}\\
& \quad \mbox{the restriction }\;\psi|_G\; \mbox{is} \ H \mbox{-}{QC \ and}\;\psi|_{\partial G}={\text{id}}_{\partial G}\big \},
\end{align*} where the abbreviation H-QC is used for H-quasiconformal and ![]() ${\text{id}}_{\partial G}$ denotes the identity map on
${\text{id}}_{\partial G}$ denotes the identity map on ![]() $\partial G$.
$\partial G$.
Originally, Teichmüller displacement problem is to determine how far a given point ![]() $x\in G$ can be mapped under a map
$x\in G$ can be mapped under a map ![]() $\psi\in \mathcal{T}_H(G)$. For the domain
$\psi\in \mathcal{T}_H(G)$. For the domain ![]() $G=\mathbb{R}^2\setminus\{(0,0),(1,0)\}$, it was shown by Teichmüller [Reference Teichmüller19] that the displacement with respect to the hyperbolic distance hG of G satisfies inequality
$G=\mathbb{R}^2\setminus\{(0,0),(1,0)\}$, it was shown by Teichmüller [Reference Teichmüller19] that the displacement with respect to the hyperbolic distance hG of G satisfies inequality
From then onwards, many researchers considered the same problem in several different settings and applied Teichmüller type results in the study of quasiconformal homogeneity of domains, see [Reference Klén, Todorčević and Vuorinen11, Reference Li, Vuorinen and Wang12, Reference Manojlović and Vuorinen14, Reference Vuorinen and Zhang23, Reference Zhou and Rasila30] and the references therein. The recent monograph by Hariri et al. [Reference Hariri, Klén and Vuorinen8] provides a chapter which systematically introduces many results and background information about Teichmüller displacement problem.
For example, Manojlović and Vuorinen [Reference Manojlović and Vuorinen14] investigated spatial quasiconformal homeomorphisms of the unit balls onto itself with identity boundary value and obtained an analogue of Teichmüller’s result. In [Reference Vuorinen and Zhang23], Vuorinen and Zhang studied the Teichmüller displacement problem with respect to the quasihyperbolic metric on uniform and convex domains with uniformly perfect boundaries. It was proved by Bonfert–Taylor et al. [Reference Bonfert–Taylor, Canary, Martin and Taylor1] that all quasiconformal homeomorphisms of hyperbolic manifolds onto itself with identity boundary value are uniformly close to isometries.
Inspired by these investigations, Zhou and Rasila [Reference Zhou and Rasila30] recently studied the Teichmüller displacement problem from the point of view of Gromov hyperbolic geometry [Reference Bridson and Haefliger4, Reference Buyalo and Schroeder5]. On the one hand, it was shown in [Reference Zhou and Rasila30, Theorem 1.1] that both the displacements with respect to the distance ratio metric jG and its modification ![]() $\widetilde{j}_G$ are bounded above for all quasiconformal homeomorphisms
$\widetilde{j}_G$ are bounded above for all quasiconformal homeomorphisms ![]() $\psi\in \mathcal{T}_H(G)$ provided
$\psi\in \mathcal{T}_H(G)$ provided ![]() $\partial G$ is uniformly perfect. For the Gromov hyperbolicity of these two metrics, we refer to [Reference Hästö7, Reference Zhou, Ponnusamy and Guan28].
$\partial G$ is uniformly perfect. For the Gromov hyperbolicity of these two metrics, we refer to [Reference Hästö7, Reference Zhou, Ponnusamy and Guan28].
On the other hand, the authors [Reference Zhou and Rasila30] investigated Teichmüller displacement problem for the class of Gromov hyperbolic domains which was introduced by Bonk et al. [Reference Bonk, Heinonen and Koskela2]. Recall that ![]() $G\subsetneq \mathbb{R}^n$ is said to be a Gromov hyperbolic domain if the domain G equipped with its quasihyperbolic metric kG is δ-hyperbolic for some
$G\subsetneq \mathbb{R}^n$ is said to be a Gromov hyperbolic domain if the domain G equipped with its quasihyperbolic metric kG is δ-hyperbolic for some ![]() $\delta\geq 0$. For a given Gromov hyperbolic domain
$\delta\geq 0$. For a given Gromov hyperbolic domain ![]() $G\subsetneq \mathbb{R}^n$ with uniformly perfect Gromov boundary
$G\subsetneq \mathbb{R}^n$ with uniformly perfect Gromov boundary ![]() $\partial_\infty G$, it was proved in [Reference Zhou and Rasila30, Theorem 1.2] that for all quasiconformal mappings
$\partial_\infty G$, it was proved in [Reference Zhou and Rasila30, Theorem 1.2] that for all quasiconformal mappings ![]() $\psi\colon G\to G$ with
$\psi\colon G\to G$ with ![]() $\psi|_{\partial_\infty G}={\text{id}}_{\partial_\infty G}$, the quasihyperbolic displacement
$\psi|_{\partial_\infty G}={\text{id}}_{\partial_\infty G}$, the quasihyperbolic displacement ![]() $k_G(x,\psi(x))$ is bounded above for all
$k_G(x,\psi(x))$ is bounded above for all ![]() $x\in G$.
$x\in G$.
It follows from [Reference Bonk, Heinonen and Koskela2, Proposition 2.8] that ![]() $(G,k_G)$ is a proper geodesic metric space. By [Reference Gehring and Osgood6, Theorem 3], we know that each quasiconformal homeomorphism
$(G,k_G)$ is a proper geodesic metric space. By [Reference Gehring and Osgood6, Theorem 3], we know that each quasiconformal homeomorphism ![]() $\psi\colon G\to G$ is a quasi-isometry with respect to the quasihyperbolic metric. Motivated by this study, we consider here the Teichmüller displacement problem on Gromov hyperbolic spaces when quasiconformal maps are replaced by quasi-isometries.
$\psi\colon G\to G$ is a quasi-isometry with respect to the quasihyperbolic metric. Motivated by this study, we consider here the Teichmüller displacement problem on Gromov hyperbolic spaces when quasiconformal maps are replaced by quasi-isometries.
1.2. Main results
Throughout this paper, we assume that (X, d) is a proper geodesic Gromov hyperbolic space with ![]() $X^*=X\cup \partial_{\infty}X$ its Gromov closure, and that
$X^*=X\cup \partial_{\infty}X$ its Gromov closure, and that ![]() $f\colon X\to X$ is a
$f\colon X\to X$ is a ![]() $(\lambda,\mu)$-quasi-isometry. The displacement of
$(\lambda,\mu)$-quasi-isometry. The displacement of ![]() $x\in X$ under f is denoted by
$x\in X$ under f is denoted by ![]() $d(x,f(x))$. The number
$d(x,f(x))$. The number ![]() $\sup\{d(x,f(x))|x\in X\}$ is called the displacement of f on X. It is not difficult to see from [Reference Bonk and Schramm3, Proposition 6.3] that f has a natural bijective extension from X to
$\sup\{d(x,f(x))|x\in X\}$ is called the displacement of f on X. It is not difficult to see from [Reference Bonk and Schramm3, Proposition 6.3] that f has a natural bijective extension from X to ![]() $\partial_\infty X$, denoted by
$\partial_\infty X$, denoted by ![]() $f|_{\partial_\infty X}$. This means that the image of any Gromov sequence under f is also Gromov. Set
$f|_{\partial_\infty X}$. This means that the image of any Gromov sequence under f is also Gromov. Set
 \begin{equation*}
\mathcal{T}_{\lambda,\mu}(X^*) =\big\{f:\,X^*\rightarrow X^*
\;\big |\; f|_X\; \mbox{is a }(\lambda,\mu)\mbox{-quasi-isometry},\;f|_{\partial_\infty X}={\text{id}}_{\partial_{\infty} X} \big\}.
\end{equation*}
\begin{equation*}
\mathcal{T}_{\lambda,\mu}(X^*) =\big\{f:\,X^*\rightarrow X^*
\;\big |\; f|_X\; \mbox{is a }(\lambda,\mu)\mbox{-quasi-isometry},\;f|_{\partial_\infty X}={\text{id}}_{\partial_{\infty} X} \big\}.
\end{equation*}Our main result is the following:
Theorem 1.1. Let ![]() $\delta,K,\mu\geq 0$ and
$\delta,K,\mu\geq 0$ and ![]() $C,\lambda\geq 1$. If (X, d) is a proper geodesic space that is δ-hyperbolic and K-roughly starlike with respect to
$C,\lambda\geq 1$. If (X, d) is a proper geodesic space that is δ-hyperbolic and K-roughly starlike with respect to ![]() $\xi\in \partial_\infty X$, and
$\xi\in \partial_\infty X$, and ![]() $\partial_\infty X$ is a C-uniformly perfect set, then there is a number
$\partial_\infty X$ is a C-uniformly perfect set, then there is a number ![]() $\Lambda=\Lambda(\delta, K, C,\lambda, \mu)$ such that
$\Lambda=\Lambda(\delta, K, C,\lambda, \mu)$ such that ![]() $d(x,f(x))\leq \Lambda$ for every
$d(x,f(x))\leq \Lambda$ for every ![]() $f\in \mathcal{T}_{\lambda,\mu}(X^*)$ and for all
$f\in \mathcal{T}_{\lambda,\mu}(X^*)$ and for all ![]() $x\in X$.
$x\in X$.
Remark 1.2. We say that ![]() $\partial_\infty X$ is a uniformly perfect set if it is C-uniformly perfect with respect to a certain visual metric. This makes sense because
$\partial_\infty X$ is a uniformly perfect set if it is C-uniformly perfect with respect to a certain visual metric. This makes sense because ![]() $\partial_\infty X$ equipped with any two visual metrics are quasimöbius to each other by [Reference Buyalo and Schroeder5, Corollary 5.2.9], and uniform perfectness is preserved under quasimöbius maps due to [Reference Wang and Zhou24, Lemma C]. Also, we note that the uniform perfectness for
$\partial_\infty X$ equipped with any two visual metrics are quasimöbius to each other by [Reference Buyalo and Schroeder5, Corollary 5.2.9], and uniform perfectness is preserved under quasimöbius maps due to [Reference Wang and Zhou24, Lemma C]. Also, we note that the uniform perfectness for ![]() $\partial_\infty X$ cannot be removed, see [Reference Zhou and Rasila30, Remark 1.1]. All connected metric spaces are uniformly perfect. For more background and applications of uniformly perfect sets in geometric function theory and analysis on metric spaces, we refer to [Reference Buyalo and Schroeder5, Reference Heinonen9, Reference Rainio, Sugawa and Vuorinen15, Reference Sugawa17, Reference Sugawa, Vuorinen and Zhang18, Reference Wang and Zhou24].
$\partial_\infty X$ cannot be removed, see [Reference Zhou and Rasila30, Remark 1.1]. All connected metric spaces are uniformly perfect. For more background and applications of uniformly perfect sets in geometric function theory and analysis on metric spaces, we refer to [Reference Buyalo and Schroeder5, Reference Heinonen9, Reference Rainio, Sugawa and Vuorinen15, Reference Sugawa17, Reference Sugawa, Vuorinen and Zhang18, Reference Wang and Zhou24].
Remark 1.3. Note that Theorem 1.1 is a generalization of [Reference Zhou and Rasila30, Theorem 1.2]. The strategy for proving Theorem 1.1 is different from that of [Reference Zhou and Rasila30, Theorem 1.2], where they applied the bounded uniformization of Gromov hyperbolic spaces due to Bonk et al. [Reference Bonk, Heinonen and Koskela2]. In this paper, our main tool is the unbounded uniformization theory, developed recently in [Reference Zhou, Ponnusamy and Rasila29].
For the definition of rough starlikeness, we refer the reader to § 2.5. We remark that if X is roughly starlike with respect to ![]() $\xi\in \partial_\infty X$, then
$\xi\in \partial_\infty X$, then ![]() $\partial_\infty X$ contains at least two points. The class of Gromov hyperbolic spaces that are roughly starlike is very large. For example, it includes metric trees, Gromov hyperbolic domains in
$\partial_\infty X$ contains at least two points. The class of Gromov hyperbolic spaces that are roughly starlike is very large. For example, it includes metric trees, Gromov hyperbolic domains in ![]() $\mathbb{R}^n$ or annular quasiconvex spaces [Reference Herron, Shanmugalingam and Xie10, Reference Väisälä22], Gromov hyperbolic manifolds [Reference Xie25], negatively curved solvable Lie groups [Reference Shanmugalingam and Xie16, Reference Xie26] and hyperbolic fillings [Reference Bonk and Schramm3, Reference Buyalo and Schroeder5]. Hence, Theorem 1.1 is valid for these Gromov hyperbolic spaces.
$\mathbb{R}^n$ or annular quasiconvex spaces [Reference Herron, Shanmugalingam and Xie10, Reference Väisälä22], Gromov hyperbolic manifolds [Reference Xie25], negatively curved solvable Lie groups [Reference Shanmugalingam and Xie16, Reference Xie26] and hyperbolic fillings [Reference Bonk and Schramm3, Reference Buyalo and Schroeder5]. Hence, Theorem 1.1 is valid for these Gromov hyperbolic spaces.
The notion of rough starlikeness with respect to a distinguished point within the space was introduced by Bonk et al. [Reference Bonk, Heinonen and Koskela2]. This concept is equivalent to the visual property defined by Bonk and Schramm [Reference Bonk and Schramm3], where they demonstrated that Gromov hyperbolic spaces with locally bounded geometry can be quasi-isometrically embedded into the classical hyperbolic spaces ![]() $\mathbb{H}^n$. This property has served as an important tool in [Reference Herron, Shanmugalingam and Xie10, Reference Zhou, Li and Rasila27, Reference Zhou and Rasila30].
$\mathbb{H}^n$. This property has served as an important tool in [Reference Herron, Shanmugalingam and Xie10, Reference Zhou, Li and Rasila27, Reference Zhou and Rasila30].
In this paper, we establish the following relationships between these two concepts in a quantitative way.
Theorem 1.4. Let X be a proper geodesic δ-hyperbolic space, where ![]() $\partial_\infty X$ contains at least two points. Then the following conditions are equivalent:
$\partial_\infty X$ contains at least two points. Then the following conditions are equivalent:
(1) X is K 1-roughly starlike with respect to
 $\xi\in \partial_\infty X$,
$\xi\in \partial_\infty X$,(2) X is K 2-roughly starlike with respect to each point of X,
(3) X is K 3-roughly starlike with respect to
 $w\in X$ and
$w\in X$ and
 \begin{equation*}
{\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq \tau_0 \gt 0,
\end{equation*}
\begin{equation*}
{\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq \tau_0 \gt 0,
\end{equation*}where
 $d_{w,\varepsilon}$ is a visual metric on
$d_{w,\varepsilon}$ is a visual metric on  $\partial_\infty X$ with parameter ɛ and base point w.
$\partial_\infty X$ with parameter ɛ and base point w.
The constants Ki, for ![]() $i=1,2,3$, depend only on each other, τ 0, and δ.
$i=1,2,3$, depend only on each other, τ 0, and δ.
In view of the above considerations, we establish the Teichmüller displacement theorem on Gromov hyperbolic spaces that is roughly starlike with respect to an interior point. Employing Theorem 1.4, we obtain the following consequence of Theorem 1.1.
Corollary 1.5. Let ![]() $\delta,K, \mu\geq 0$,
$\delta,K, \mu\geq 0$, ![]() $C,\lambda\geq 1$ and ϑ > 0. Suppose (X, d) is a proper geodesic δ-hyperbolic space and K-roughly starlike with respect to
$C,\lambda\geq 1$ and ϑ > 0. Suppose (X, d) is a proper geodesic δ-hyperbolic space and K-roughly starlike with respect to ![]() $w\in X$. If
$w\in X$. If ![]() $\partial_\infty X$ is a C-uniformly perfect set with
$\partial_\infty X$ is a C-uniformly perfect set with ![]() $\vartheta={\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \gt 0$, then there is a number
$\vartheta={\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \gt 0$, then there is a number ![]() $\Lambda_1=\Lambda_1(\delta, K, C,\lambda, \mu,\vartheta)$ such that
$\Lambda_1=\Lambda_1(\delta, K, C,\lambda, \mu,\vartheta)$ such that ![]() $d(x,f(x))\leq \Lambda_1$ for all
$d(x,f(x))\leq \Lambda_1$ for all ![]() $x\in X$ and for every
$x\in X$ and for every ![]() $f\in \mathcal{T}_{\lambda,\mu}(X^*)$.
$f\in \mathcal{T}_{\lambda,\mu}(X^*)$.
This paper is organized as follows. In § 2, we focus on Gromov hyperbolic geometry and properties of quasi-isometries, and then we prove Theorem 1.4. The proof of Theorem 1.1 is given in § 3. In § 4, we provide two examples and some applications of our main results.
2. Gromov hyperbolic spaces and quasi-isometric maps
2.1. Metric geometry
Let (Z, d) be a metric space. The open ball and the closed ball of radius r centred at ![]() $x\in Z$ are denoted by
$x\in Z$ are denoted by ![]() $B(x,r)$ and
$B(x,r)$ and ![]() $\overline{B}(x,r)$, respectively. The space Z is called proper if its closed balls are compact. We use
$\overline{B}(x,r)$, respectively. The space Z is called proper if its closed balls are compact. We use ![]() ${\text{diam}}(W)$ to denote the diameter of a set
${\text{diam}}(W)$ to denote the diameter of a set ![]() $W\subset Z$. For
$W\subset Z$. For ![]() $C\geq 1$, a metric space Z is called C-uniformly perfect, if for each
$C\geq 1$, a metric space Z is called C-uniformly perfect, if for each ![]() $x\in Z$ and every r > 0,
$x\in Z$ and every r > 0, ![]() $B(x,r)\setminus B(x, r/C)\not=\emptyset$ provided
$B(x,r)\setminus B(x, r/C)\not=\emptyset$ provided ![]() $Z\setminus B(x,r)\not=\emptyset$.
$Z\setminus B(x,r)\not=\emptyset$.
A geodesic arc α between x and y in Z is a map ![]() $\alpha\colon I=[0,l]\to Z$ from an interval I to Z such that
$\alpha\colon I=[0,l]\to Z$ from an interval I to Z such that ![]() $\alpha(0)=x$,
$\alpha(0)=x$, ![]() $\alpha(l)=y$, and
$\alpha(l)=y$, and ![]() $d(\alpha(t),\alpha(t'))=|t-t'|$ for all
$d(\alpha(t),\alpha(t'))=|t-t'|$ for all ![]() $t,t'\in I$. If
$t,t'\in I$. If ![]() $I=[0,\infty)$, then α is called a geodesic ray. If
$I=[0,\infty)$, then α is called a geodesic ray. If ![]() $I=\mathbb{R}$, then α is called a geodesic line. The space Z is said to be geodesic if every pair of points can be connected with a geodesic arc. Let
$I=\mathbb{R}$, then α is called a geodesic line. The space Z is said to be geodesic if every pair of points can be connected with a geodesic arc. Let ![]() $[x,y]$ denote the geodesic between x and y in Z.
$[x,y]$ denote the geodesic between x and y in Z.
2.2. Maps
The identity map of a set W is denoted by ![]() ${\text{id}}_W$. Let
${\text{id}}_W$. Let ![]() $f\colon $
$f\colon $ ![]() $(Z,d)\to (Z',d')$ be a map (not necessarily continuous) between metric spaces Z and Zʹ, and let
$(Z,d)\to (Z',d')$ be a map (not necessarily continuous) between metric spaces Z and Zʹ, and let ![]() $\lambda\geq 1$ and
$\lambda\geq 1$ and ![]() $\mu\geq 0$ be constants. We say that f is a
$\mu\geq 0$ be constants. We say that f is a ![]() $(\lambda, \mu)$-quasi-isometric map if for all
$(\lambda, \mu)$-quasi-isometric map if for all ![]() $x,y\in Z$,
$x,y\in Z$,
If in addition, every point ![]() $y\in Z'$ has the distance at most µ from the set f(Z), then f is called a
$y\in Z'$ has the distance at most µ from the set f(Z), then f is called a ![]() $(\lambda, \mu)$-quasi-isometry. Moreover, if f is a homeomorphism and µ = 0, then it is called a λ-bilipschitz map. A curve
$(\lambda, \mu)$-quasi-isometry. Moreover, if f is a homeomorphism and µ = 0, then it is called a λ-bilipschitz map. A curve ![]() $\gamma\colon I\to Z$ is called a
$\gamma\colon I\to Z$ is called a ![]() $(\lambda,\mu)$-quasigeodesic if γ is a
$(\lambda,\mu)$-quasigeodesic if γ is a ![]() $(\lambda,\mu)$-quasi-isometric map.
$(\lambda,\mu)$-quasi-isometric map.
2.3. Gromov hyperbolicity
Let (X, d) be a metric space. Fix a base point ![]() $w\in X$. For
$w\in X$. For ![]() $x,y\in X$, we define
$x,y\in X$, we define
 \begin{equation*}
(x|y)_w=\frac{1}{2}\big(d(x,w)+d(y,w)-d(x,y)\big).
\end{equation*}
\begin{equation*}
(x|y)_w=\frac{1}{2}\big(d(x,w)+d(y,w)-d(x,y)\big).
\end{equation*} This number is called the Gromov product of x and y with respect to w. We say that X is Gromov hyperbolic, if there is a constant ![]() $\delta\geq 0$ such that
$\delta\geq 0$ such that
In this paper, we assume that Gromov hyperbolic spaces are unbounded.
Suppose X is a Gromov hyperbolic space. A sequence ![]() $\{x_i\}$ in X is called a Gromov sequence if
$\{x_i\}$ in X is called a Gromov sequence if ![]() $(x_i|x_j)_w\rightarrow \infty$ as
$(x_i|x_j)_w\rightarrow \infty$ as ![]() $i,$
$i,$ ![]() $j\rightarrow \infty.$ Two such sequences
$j\rightarrow \infty.$ Two such sequences ![]() $\{x_i\}$ and
$\{x_i\}$ and ![]() $\{y_j\}$ are said to be equivalent if
$\{y_j\}$ are said to be equivalent if ![]() $(x_i|y_i)_w\rightarrow \infty$ as
$(x_i|y_i)_w\rightarrow \infty$ as ![]() $i\to\infty$. The Gromov boundary
$i\to\infty$. The Gromov boundary ![]() $\partial_\infty X$ of X is defined to be the set of all equivalence classes of Gromov sequences, and
$\partial_\infty X$ of X is defined to be the set of all equivalence classes of Gromov sequences, and ![]() $X^*=X \cup \partial_\infty X$ is called the Gromov closure of X. If (X, d) is proper geodesic, then the Gromov boundary is also equivalent to the geodesic boundary, which is defined as the set of equivalence classes of geodesic rays, where two geodesic rays are equivalent if they have finite Hausdorff distance.
$X^*=X \cup \partial_\infty X$ is called the Gromov closure of X. If (X, d) is proper geodesic, then the Gromov boundary is also equivalent to the geodesic boundary, which is defined as the set of equivalence classes of geodesic rays, where two geodesic rays are equivalent if they have finite Hausdorff distance.
Lemma 2.1. ![]() $($[Reference Bridson and Haefliger4, Chapter III.H. Lemmas 3.1 and 3.2]
$($[Reference Bridson and Haefliger4, Chapter III.H. Lemmas 3.1 and 3.2]![]() $)$ Suppose that X is a proper geodesic space that is δ-hyperbolic. Then for each
$)$ Suppose that X is a proper geodesic space that is δ-hyperbolic. Then for each ![]() $x\in X$ and
$x\in X$ and ![]() $\xi\in \partial_\infty X$, there exists a geodesic ray
$\xi\in \partial_\infty X$, there exists a geodesic ray ![]() $\gamma\colon [0,\infty)\to X$ with
$\gamma\colon [0,\infty)\to X$ with ![]() $\gamma(0)=x$ and
$\gamma(0)=x$ and ![]() $\gamma(\infty)=\xi$. Similarly, for each pair of distinct points
$\gamma(\infty)=\xi$. Similarly, for each pair of distinct points ![]() $\xi,\eta\in \partial_\infty X$, there exists a geodesic line
$\xi,\eta\in \partial_\infty X$, there exists a geodesic line ![]() $\gamma\colon \mathbb{R}\to X$ with
$\gamma\colon \mathbb{R}\to X$ with ![]() $\gamma(-\infty)=\xi$ and
$\gamma(-\infty)=\xi$ and ![]() $\gamma(\infty)=\eta$.
$\gamma(\infty)=\eta$.
For all ![]() $x\in X$ and
$x\in X$ and ![]() $\xi\in \partial_\infty X$, the Gromov product
$\xi\in \partial_\infty X$, the Gromov product ![]() $(x|\xi)_w$ of x and ξ is defined by
$(x|\xi)_w$ of x and ξ is defined by ![]() $(x|\xi)_w= \inf\{\liminf_{i\rightarrow \infty}(x|y_i)_w\;|\; \{y_i\}\in \xi\}.$ For all
$(x|\xi)_w= \inf\{\liminf_{i\rightarrow \infty}(x|y_i)_w\;|\; \{y_i\}\in \xi\}.$ For all ![]() $\xi,$
$\xi,$ ![]() $\zeta\in \partial_\infty X$, the Gromov product
$\zeta\in \partial_\infty X$, the Gromov product ![]() $(\xi|\zeta)_w$ of ξ and ζ is defined by
$(\xi|\zeta)_w$ of ξ and ζ is defined by ![]() $(\xi|\zeta)_w= \inf \{\liminf_{i\rightarrow \infty}(x_i|y_i)_w\;|\; \{x_i\}\in \xi\;\;{\rm and}\;\; \{y_i\}\in \zeta\}.$
$(\xi|\zeta)_w= \inf \{\liminf_{i\rightarrow \infty}(x_i|y_i)_w\;|\; \{x_i\}\in \xi\;\;{\rm and}\;\; \{y_i\}\in \zeta\}.$
Next, we recall the following results about the Gromov product.
Lemma 2.2. ![]() $($[Reference Väisälä21, Lemma 5.11]
$($[Reference Väisälä21, Lemma 5.11]![]() $)$ Let X be a δ-hyperbolic space with
$)$ Let X be a δ-hyperbolic space with ![]() $o,z\in X$, and let
$o,z\in X$, and let ![]() $\xi,\xi'\in\partial_\infty X$. Then for any sequences
$\xi,\xi'\in\partial_\infty X$. Then for any sequences ![]() $\{y_i\}\in \xi$,
$\{y_i\}\in \xi$, ![]() $\{y_i'\}\in \xi'$, we have
$\{y_i'\}\in \xi'$, we have
(1)
 $(z|\xi)_o\leq \liminf\limits_{i\rightarrow \infty} (z|y_i)_o \leq \limsup\limits_{i\rightarrow \infty} (z|y_i)_o\leq (z|\xi)_o+\delta;$
$(z|\xi)_o\leq \liminf\limits_{i\rightarrow \infty} (z|y_i)_o \leq \limsup\limits_{i\rightarrow \infty} (z|y_i)_o\leq (z|\xi)_o+\delta;$(2)
 $(\xi|\xi')_o\leq \liminf\limits_{i\rightarrow \infty} (y_i|y_i')_o \leq \limsup\limits_{i\rightarrow \infty} (y_i|y_i')_o\leq (\xi|\xi')_o+2\delta.$
$(\xi|\xi')_o\leq \liminf\limits_{i\rightarrow \infty} (y_i|y_i')_o \leq \limsup\limits_{i\rightarrow \infty} (y_i|y_i')_o\leq (\xi|\xi')_o+2\delta.$
Let (X, d) be a δ-hyperbolic space and ![]() $w\in X$ be given. For
$w\in X$ be given. For ![]() $0 \lt \varepsilon \lt \min\{1, 1/(5\delta)\}$, we define
$0 \lt \varepsilon \lt \min\{1, 1/(5\delta)\}$, we define
 \begin{equation*}\rho_{w,\varepsilon}(\xi,\zeta)=\mathrm{e}^{-\varepsilon(\xi|\zeta)_w}\end{equation*}
\begin{equation*}\rho_{w,\varepsilon}(\xi,\zeta)=\mathrm{e}^{-\varepsilon(\xi|\zeta)_w}\end{equation*} for all ξ and ζ in the Gromov boundary ![]() $\partial_\infty X$ of X with the convention that
$\partial_\infty X$ of X with the convention that ![]() $\mathrm{e}^{-\infty}=0$.
$\mathrm{e}^{-\infty}=0$.
We now define
 \begin{equation*}d_{w,\varepsilon} (\xi,\zeta):=\inf \left\{\sum_{i=1}^{n} \rho_{w,\varepsilon} (\xi_{i-1},\xi_i)\;\big |\;n\geq 1,\xi=\xi_0,\xi_1,\ldots,\xi_n=\zeta\in \partial_\infty X \right\}.\end{equation*}
\begin{equation*}d_{w,\varepsilon} (\xi,\zeta):=\inf \left\{\sum_{i=1}^{n} \rho_{w,\varepsilon} (\xi_{i-1},\xi_i)\;\big |\;n\geq 1,\xi=\xi_0,\xi_1,\ldots,\xi_n=\zeta\in \partial_\infty X \right\}.\end{equation*} Then ![]() $(\partial_\infty X,d_{w,\varepsilon})$ is a metric space with
$(\partial_\infty X,d_{w,\varepsilon})$ is a metric space with
 \begin{equation} \frac{1}{2}\rho_{w,\varepsilon}\leq d_{w,\varepsilon}\leq \rho_{w,\varepsilon},\end{equation}
\begin{equation} \frac{1}{2}\rho_{w,\varepsilon}\leq d_{w,\varepsilon}\leq \rho_{w,\varepsilon},\end{equation} and we call ![]() $d_{w,\varepsilon}$ the visual metric of
$d_{w,\varepsilon}$ the visual metric of ![]() $\partial_\infty X$ with base point
$\partial_\infty X$ with base point ![]() $w\in X$ and parameter ɛ.
$w\in X$ and parameter ɛ.
2.4. Busemann functions
Let (X, d) be a Gromov δ-hyperbolic space with ![]() $o\in X$ and
$o\in X$ and ![]() $\xi\in\partial_\infty X$. Let
$\xi\in\partial_\infty X$. Let ![]() $\mathcal{B}(\xi)$ be the class of Busemann functions based at ξ; see [Reference Buyalo and Schroeder5, Section 3.1] for more background information. Let
$\mathcal{B}(\xi)$ be the class of Busemann functions based at ξ; see [Reference Buyalo and Schroeder5, Section 3.1] for more background information. Let ![]() $b\in \mathcal{B}(\xi)$ be a Busemann function. For all
$b\in \mathcal{B}(\xi)$ be a Busemann function. For all ![]() $x\in X$,
$x\in X$,
We define the Gromov product of ![]() $x,y\in X$ with respect to the Busemann function
$x,y\in X$ with respect to the Busemann function ![]() $b\in \mathcal{B}(\xi)$ as
$b\in \mathcal{B}(\xi)$ as
 \begin{equation*}
(x|y)_b=\frac{1}{2}(b(x)+b(y)-d(x,y)).
\end{equation*}
\begin{equation*}
(x|y)_b=\frac{1}{2}(b(x)+b(y)-d(x,y)).
\end{equation*} Similarly, for ![]() $x\in X$ and
$x\in X$ and ![]() $\zeta\in \partial_\infty X\setminus\{\xi\}$, the Gromov product
$\zeta\in \partial_\infty X\setminus\{\xi\}$, the Gromov product ![]() $(x|\zeta)_b$ of x and ζ based at b is defined by
$(x|\zeta)_b$ of x and ζ based at b is defined by ![]() $(x|\zeta)_b= \inf\{\liminf_{i\rightarrow \infty}(x|z_i)_b\; |\; \{z_i\}\in \zeta\}.$ For points ξ 1 and ξ 2 belonging to
$(x|\zeta)_b= \inf\{\liminf_{i\rightarrow \infty}(x|z_i)_b\; |\; \{z_i\}\in \zeta\}.$ For points ξ 1 and ξ 2 belonging to ![]() $\partial_\infty X\setminus\{\xi\}$, we define their Gromov product based at b by
$\partial_\infty X\setminus\{\xi\}$, we define their Gromov product based at b by ![]() $(\xi_1|\xi_2)_b=\inf\{\liminf_{i\to\infty} (x_i|y_i)_b\;|\; \{x_i\}\in\xi_1 , \{y_i\}\in\xi_2\}.$
$(\xi_1|\xi_2)_b=\inf\{\liminf_{i\to\infty} (x_i|y_i)_b\;|\; \{x_i\}\in\xi_1 , \{y_i\}\in\xi_2\}.$
For ɛ > 0 with ![]() $\mathrm{e}^{22\varepsilon\delta}\leq 2$, we define
$\mathrm{e}^{22\varepsilon\delta}\leq 2$, we define
 \begin{equation*}
\rho_{b,\varepsilon}(\xi_1,\xi_2)= \mathrm{e}^{-\varepsilon(\xi_1|\xi_2)_b}\;\;\;\;\;\;\;\mbox{for all}\,\xi_1,\xi_2\in \partial_\infty X\setminus\{\xi\}.
\end{equation*}
\begin{equation*}
\rho_{b,\varepsilon}(\xi_1,\xi_2)= \mathrm{e}^{-\varepsilon(\xi_1|\xi_2)_b}\;\;\;\;\;\;\;\mbox{for all}\,\xi_1,\xi_2\in \partial_\infty X\setminus\{\xi\}.
\end{equation*} Then for ![]() $i=1,2,3$ with
$i=1,2,3$ with ![]() $\xi_i\in \partial_\infty X\setminus\{\xi\}$, we have
$\xi_i\in \partial_\infty X\setminus\{\xi\}$, we have
 \begin{equation*}
\rho_{b,\varepsilon}(\xi_1,\xi_2)\leq \mathrm{e}^{22\varepsilon\delta} \max\{\rho_{b,\varepsilon}(\xi_1,\xi_3),\rho_{b,\varepsilon}(\xi_3,\xi_2)\}.
\end{equation*}
\begin{equation*}
\rho_{b,\varepsilon}(\xi_1,\xi_2)\leq \mathrm{e}^{22\varepsilon\delta} \max\{\rho_{b,\varepsilon}(\xi_1,\xi_3),\rho_{b,\varepsilon}(\xi_3,\xi_2)\}.
\end{equation*}We now define
 \begin{equation*}
d_{b,\varepsilon}(\omega,\zeta):=\inf\left \{\sum_{i=1}^{m} \rho_{b,\varepsilon} (\zeta_{i-1},\zeta_i)\;|\;m\geq 1,\zeta=\zeta_0,\zeta_1,\ldots,\zeta_m=\omega\in\partial_\infty X\setminus\{\xi\}\right\}.
\end{equation*}
\begin{equation*}
d_{b,\varepsilon}(\omega,\zeta):=\inf\left \{\sum_{i=1}^{m} \rho_{b,\varepsilon} (\zeta_{i-1},\zeta_i)\;|\;m\geq 1,\zeta=\zeta_0,\zeta_1,\ldots,\zeta_m=\omega\in\partial_\infty X\setminus\{\xi\}\right\}.
\end{equation*} By [Reference Buyalo and Schroeder5, Lemma 3.3.3], it follows that ![]() $(\partial_\infty X\setminus\{\xi\}, d_{b,\varepsilon})$ is a metric space such that
$(\partial_\infty X\setminus\{\xi\}, d_{b,\varepsilon})$ is a metric space such that ![]() $\rho_{b,\varepsilon}/2 \leq d_{b,\varepsilon}\leq \rho_{b,\varepsilon}.$ We call
$\rho_{b,\varepsilon}/2 \leq d_{b,\varepsilon}\leq \rho_{b,\varepsilon}.$ We call ![]() $d_{b,\varepsilon}$ a Hamenstädt metric on the punctured space
$d_{b,\varepsilon}$ a Hamenstädt metric on the punctured space ![]() $\partial_\infty X\setminus\{\xi\}$ based at ξ with parameter ɛ.
$\partial_\infty X\setminus\{\xi\}$ based at ξ with parameter ɛ.
2.5. Rough starlikeness
We first recall the definition of rough starlikeness of Gromov hyperbolic spaces. See [Reference Bonk, Heinonen and Koskela2, Reference Herron, Shanmugalingam and Xie10, Reference Väisälä22, Reference Zhou, Li and Rasila27, Reference Zhou and Rasila30] for more information and backgrounds on this topic.
Let X be a proper geodesic δ-hyperbolic space, ![]() $w\in X$,
$w\in X$, ![]() $\xi\in\partial_\infty X$ and
$\xi\in\partial_\infty X$ and ![]() $K\geq 0$.
$K\geq 0$.
Definition 2.4. We say that X is K-roughly starlike with respect to ξ if for each ![]() $x\in X$, there is a point
$x\in X$, there is a point ![]() $\zeta\in\partial_\infty X$ and a geodesic line
$\zeta\in\partial_\infty X$ and a geodesic line ![]() $\gamma=[\xi,\zeta]$ connecting ξ and ζ such that
$\gamma=[\xi,\zeta]$ connecting ξ and ζ such that ![]() ${\text{dist}}(x,\gamma)\leq K.$
${\text{dist}}(x,\gamma)\leq K.$
Definition 2.5. We say that X is K-roughly starlike with respect to w if for each ![]() $x\in X$, there is a point
$x\in X$, there is a point ![]() $\zeta\in\partial_\infty X$ and a geodesic ray
$\zeta\in\partial_\infty X$ and a geodesic ray ![]() $\gamma=[w,\zeta]$ emanating from w to ζ such that
$\gamma=[w,\zeta]$ emanating from w to ζ such that ![]() ${\text{dist}}(x,\gamma)\leq K.$
${\text{dist}}(x,\gamma)\leq K.$
Next, we show that the rough starlikeness of Gromov hyperbolic spaces is preserved under quasi-isometries. Although this result is well-known, we have failed to find a reference containing its proof. For completeness, we give a proof here.
Lemma 2.6. Let ![]() $\delta,K,\mu\geq 0,$
$\delta,K,\mu\geq 0,$ ![]() $\lambda\geq 1$ and let
$\lambda\geq 1$ and let ![]() $f\colon (X,d)\to (X',d')$ be a
$f\colon (X,d)\to (X',d')$ be a ![]() $(\lambda,\mu)$-quasi-isometry between proper geodesic δ-hyperbolic spaces. We have the following:
$(\lambda,\mu)$-quasi-isometry between proper geodesic δ-hyperbolic spaces. We have the following:
(1) If X is K-roughly starlike with respect to
 $\xi\in\partial_\infty X$, then Xʹ is Kʹ-roughly starlike with respect to a point
$\xi\in\partial_\infty X$, then Xʹ is Kʹ-roughly starlike with respect to a point  $\xi'\in\partial_\infty X'$, where
$\xi'\in\partial_\infty X'$, where  $K'=K'(\delta,K,\mu,\lambda)$;
$K'=K'(\delta,K,\mu,\lambda)$;(2) If X is K-roughly starlike with respect to
 $w\in X$, then Xʹ is Kʹ-roughly starlike with respect to a point
$w\in X$, then Xʹ is Kʹ-roughly starlike with respect to a point  $w'\in X'$, where
$w'\in X'$, where  $K'=K'(\delta,K,\mu,\lambda)$.
$K'=K'(\delta,K,\mu,\lambda)$.
Proof. We only prove (1), because the proof of (2) is similar. It follows from [Reference Bonk and Schramm3, Proposition 6.3] that f induces a bijective map ![]() $f\colon \partial_\infty X \to \partial_\infty X'$. Let
$f\colon \partial_\infty X \to \partial_\infty X'$. Let ![]() $\xi'=f(\xi)$. Then we check that Xʹ is Kʹ-roughly starlike with respect to the point
$\xi'=f(\xi)$. Then we check that Xʹ is Kʹ-roughly starlike with respect to the point ![]() $\xi'\in\partial_\infty X'$, where
$\xi'\in\partial_\infty X'$, where ![]() $K'=K'(\delta,K,\mu,\lambda)$.
$K'=K'(\delta,K,\mu,\lambda)$.
On the one hand, for a given ![]() $x'\in X'$, there is an
$x'\in X'$, there is an ![]() $x\in X$ such that
$x\in X$ such that
As X is K-roughly starlike with respect to ![]() $\xi\in\partial_\infty X$, there is a
$\xi\in\partial_\infty X$, there is a ![]() $\zeta\in \partial_\infty X$ and a geodesic line
$\zeta\in \partial_\infty X$ and a geodesic line ![]() $\gamma=[\xi,\zeta]$ joining ξ and ζ such that
$\gamma=[\xi,\zeta]$ joining ξ and ζ such that
On the other hand, because ![]() $f\colon X\to X'$ is a
$f\colon X\to X'$ is a ![]() $(\lambda,\mu)$-quasi-isometry, we see that
$(\lambda,\mu)$-quasi-isometry, we see that ![]() $f(\gamma)$ is a
$f(\gamma)$ is a ![]() $(\lambda,\mu)$-quasigeodesic line with endpoints
$(\lambda,\mu)$-quasigeodesic line with endpoints ![]() $\xi'=f(\xi)$ and
$\xi'=f(\xi)$ and ![]() $\zeta'=f(\zeta)$. Furthermore, because Xʹ is a proper geodesic δ-hyperbolic space, by [Reference Herron, Shanmugalingam and Xie10, Lemma 3.5], it follows that there is a geodesic line
$\zeta'=f(\zeta)$. Furthermore, because Xʹ is a proper geodesic δ-hyperbolic space, by [Reference Herron, Shanmugalingam and Xie10, Lemma 3.5], it follows that there is a geodesic line ![]() $\alpha=[\xi',\zeta']$ joining
$\alpha=[\xi',\zeta']$ joining ![]() $\xi'$ and
$\xi'$ and ![]() $\zeta'$ such that the Hausdorff distance satisfies the inequality
$\zeta'$ such that the Hausdorff distance satisfies the inequality
for some constant ![]() $M=M(\lambda,\mu,\delta)$. Therefore, we obtain from Equations (2.7), (2.8) and (2.4) that
$M=M(\lambda,\mu,\delta)$. Therefore, we obtain from Equations (2.7), (2.8) and (2.4) that
The lemma follows.
Finally, we are ready to supply the proof of Theorem 1.4 which connects the above two notions of rough starlikeness.
2.6. Proof of Theorem 1.4
Suppose that X is a proper geodesic δ-hyperbolic space, and ![]() $\partial_\infty X$ contains at least two points.
$\partial_\infty X$ contains at least two points.
![]() $(1) \Rightarrow (2):$ Let
$(1) \Rightarrow (2):$ Let ![]() $w\in X$. For each
$w\in X$. For each ![]() $x\in X$, there is a point
$x\in X$, there is a point ![]() $\xi_x\in \partial_\infty X$ and a geodesic line
$\xi_x\in \partial_\infty X$ and a geodesic line ![]() $[\xi,\xi_x]$ connecting ξ and ξx such that
$[\xi,\xi_x]$ connecting ξ and ξx such that
because X is K 1-roughly starlike with respect to ξ. By Lemma 2.1, it follows that there are two geodesic rays ![]() $[w,\xi]$ and
$[w,\xi]$ and ![]() $[w,\xi_x]$ joining w to ξ and ξx, respectively. Considering the extended geodesic triangle
$[w,\xi_x]$ joining w to ξ and ξx, respectively. Considering the extended geodesic triangle ![]() $\Delta=[w,\xi_x]\cup [\xi_x,\xi] \cup [\xi,w]$ and then applying [Reference Väisälä21, Theorem 6.24], we see that there is a positive integer N such that
$\Delta=[w,\xi_x]\cup [\xi_x,\xi] \cup [\xi,w]$ and then applying [Reference Väisälä21, Theorem 6.24], we see that there is a positive integer N such that
This inequality, together with Equation ![]() $(2.10)$, shows that
$(2.10)$, shows that
as desired.
![]() $(2) \Rightarrow (3):$ Because
$(2) \Rightarrow (3):$ Because ![]() $\partial_\infty X$ contains at least two points, we may choose two distinct points ξ and ζ from
$\partial_\infty X$ contains at least two points, we may choose two distinct points ξ and ζ from ![]() $\partial_\infty X$. By Lemma 2.1, it follows that there is a geodesic line
$\partial_\infty X$. By Lemma 2.1, it follows that there is a geodesic line ![]() $[\xi,\zeta]$ connecting ξ to ζ. Now, fix a point
$[\xi,\zeta]$ connecting ξ to ζ. Now, fix a point ![]() $w\in X$ in the line
$w\in X$ in the line ![]() $[\xi,\zeta]$. By Lemma 2.2, we find that
$[\xi,\zeta]$. By Lemma 2.2, we find that ![]() $(\xi|\zeta)_w\leq 2\delta.$ Therefore, by Equation (2.3), we obtain that
$(\xi|\zeta)_w\leq 2\delta.$ Therefore, by Equation (2.3), we obtain that
 \begin{equation*}
{\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq d_{w,\varepsilon}(\xi,\zeta)\geq \frac{1}{2} \mathrm{e}^{-\varepsilon (\xi|\zeta)_w} \geq \frac{1}{2} \mathrm{e}^{-2\varepsilon\delta}=:\tau_0,
\end{equation*}
\begin{equation*}
{\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq d_{w,\varepsilon}(\xi,\zeta)\geq \frac{1}{2} \mathrm{e}^{-\varepsilon (\xi|\zeta)_w} \geq \frac{1}{2} \mathrm{e}^{-2\varepsilon\delta}=:\tau_0,
\end{equation*}as required.
![]() $(3) \Rightarrow (1):$ Because
$(3) \Rightarrow (1):$ Because ![]() ${\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq \tau_0 \gt 0$, we see from Equation (2.3) that there are two points ξ and ζ in
${\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \geq \tau_0 \gt 0$, we see from Equation (2.3) that there are two points ξ and ζ in ![]() $\partial_\infty X$ such that
$\partial_\infty X$ such that
 \begin{equation*}
\tau_0\leq d_{w,\varepsilon}(\xi,\zeta)\leq \mathrm{e}^{-\varepsilon (\xi|\zeta)_w},
\end{equation*}
\begin{equation*}
\tau_0\leq d_{w,\varepsilon}(\xi,\zeta)\leq \mathrm{e}^{-\varepsilon (\xi|\zeta)_w},
\end{equation*}which implies that
 \begin{equation*}
(\xi|\zeta)_w \leq \frac{1}{\varepsilon}\log \frac{1}{\tau_0}.
\end{equation*}
\begin{equation*}
(\xi|\zeta)_w \leq \frac{1}{\varepsilon}\log \frac{1}{\tau_0}.
\end{equation*} Again, by Lemma 2.1, there is a geodesic line ![]() $[\xi,\zeta]$ connecting ξ to ζ. Moreover, by the extended standard estimate (cf. [Reference Väisälä21, 6.20]), it follows that there is a positive integer
$[\xi,\zeta]$ connecting ξ to ζ. Moreover, by the extended standard estimate (cf. [Reference Väisälä21, 6.20]), it follows that there is a positive integer ![]() $N_1\geq 0$ such that
$N_1\geq 0$ such that
 \begin{equation*}
{\text{dist}}(w, [\xi,\zeta] )\leq (\xi|\zeta)_w +N_1 \delta\leq \frac{1}{\varepsilon}\log \frac{1}{\tau_0}+N_1 \delta=:C_2.
\end{equation*}
\begin{equation*}
{\text{dist}}(w, [\xi,\zeta] )\leq (\xi|\zeta)_w +N_1 \delta\leq \frac{1}{\varepsilon}\log \frac{1}{\tau_0}+N_1 \delta=:C_2.
\end{equation*} Thus there is a point ![]() $w_0\in [\xi,\zeta]$ such that
$w_0\in [\xi,\zeta]$ such that
Now, we check that X is K 1-roughly starlike with respect to ξ with a constant ![]() $K_1\geq 0$ depending only on δ that will be decided below.
$K_1\geq 0$ depending only on δ that will be decided below.
Fix ![]() $x\in X$. Because X is K 3-roughly starlike with respect to w, there is a point
$x\in X$. Because X is K 3-roughly starlike with respect to w, there is a point ![]() $\xi_x \in\partial_\infty X$ and a geodesic ray
$\xi_x \in\partial_\infty X$ and a geodesic ray ![]() $[w,\xi_x]$ connecting w and ξx such that
$[w,\xi_x]$ connecting w and ξx such that
Lemma 2.1 ensures that there is a geodesic ray ![]() $[w_0,\xi_x]$ joining w 0 to ξx. Because
$[w_0,\xi_x]$ joining w 0 to ξx. Because ![]() $d(w,w_0)\leq C_2$, by the Closeness Lemma (cf. [Reference Väisälä21, 6.9]), we have the following Hausdorff distance:
$d(w,w_0)\leq C_2$, by the Closeness Lemma (cf. [Reference Väisälä21, 6.9]), we have the following Hausdorff distance:
for some positive integer N 2.
Pick a geodesic line ![]() $[\xi,\xi_x]$ connecting ξ to ξx and consider the extended geodesic triangle
$[\xi,\xi_x]$ connecting ξ to ξx and consider the extended geodesic triangle ![]() $\Delta=[w_0,\xi_x]\cup [\xi_x,\xi] \cup [\xi,w_0]$. Now it follows from [Reference Väisälä21, Theorem 6.24] that there is a positive integer N 3 such that for all
$\Delta=[w_0,\xi_x]\cup [\xi_x,\xi] \cup [\xi,w_0]$. Now it follows from [Reference Väisälä21, Theorem 6.24] that there is a positive integer N 3 such that for all ![]() $z\in [w_0,\xi_x]$,
$z\in [w_0,\xi_x]$,
Hence we obtain from Equations ![]() $(2.11)$,
$(2.11)$, ![]() $(2.12)$ and
$(2.12)$ and ![]() $(2.13)$ that
$(2.13)$ that
This implies that
completing the proof.
3. Teichmüller displacement theorem
In this section, we study Teichmüller displacement problem on Gromov hyperbolic spaces in a quantitative way and prove Theorem 1.1. For the proof of Theorem 1.1, we use the unbounded uniformization procedure that was developed recently in [Reference Zhou, Ponnusamy and Rasila29]. We begin with some definitions.
3.1. Quasihyperbolic metric and uniform spaces
Let ![]() $(\Omega, d)$ be a metric space. The metric completion and metric boundary of Ω are denoted by
$(\Omega, d)$ be a metric space. The metric completion and metric boundary of Ω are denoted by ![]() $\overline{\Omega}$ and
$\overline{\Omega}$ and ![]() $\partial \Omega=\overline{\Omega}\setminus \Omega$, respectively. The space Ω is incomplete if
$\partial \Omega=\overline{\Omega}\setminus \Omega$, respectively. The space Ω is incomplete if ![]() $\partial \Omega\neq \emptyset$. For
$\partial \Omega\neq \emptyset$. For ![]() $z\in \Omega$, the distance between z and
$z\in \Omega$, the distance between z and ![]() $\partial \Omega$ is denoted by
$\partial \Omega$ is denoted by ![]() $d(z)={\text{dist}}(z,\partial \Omega)$.
$d(z)={\text{dist}}(z,\partial \Omega)$.
In this subsection, we assume that ![]() $(\Omega, d)$ is an incomplete, locally compact and rectifiably connected metric space, and that the identity map
$(\Omega, d)$ is an incomplete, locally compact and rectifiably connected metric space, and that the identity map ![]() $(\Omega,d)\to (\Omega,\ell)$ is continuous, where
$(\Omega,d)\to (\Omega,\ell)$ is continuous, where ![]() $\ell$ is the length metric of Ω induced by d. See [Reference Bonk, Heinonen and Koskela2, Appendix] for more discussions.
$\ell$ is the length metric of Ω induced by d. See [Reference Bonk, Heinonen and Koskela2, Appendix] for more discussions.
Definition 3.1. As in [Reference Bonk, Heinonen and Koskela2], the quasihyperbolic metric k in ![]() $(\Omega, d)$ is defined by
$(\Omega, d)$ is defined by
 \begin{equation*}
k(x, y)=\inf_{\alpha} \int_{\alpha} \frac{ds}{d(z)} ,
\end{equation*}
\begin{equation*}
k(x, y)=\inf_{\alpha} \int_{\alpha} \frac{ds}{d(z)} ,
\end{equation*}where the infimum is taken over all rectifiable curves α in Ω connecting x and y and ds denotes the arc length element with respect to the metric d.
It follows from [Reference Bonk, Heinonen and Koskela2, Proposition 2.8] that ![]() $(\Omega,k)$ is a proper geodesic space. Next we recall the definition of uniform spaces from the work of Bonk et al. [Reference Bonk, Heinonen and Koskela2] and use this to establish their bounded uniformization theory of Gromov hyperbolic spaces. For more backgrounds, we refer to [Reference Herron, Shanmugalingam and Xie10, Reference Vuorinen and Zhang23, Reference Zhou, Li and Rasila27] and the references therein.
$(\Omega,k)$ is a proper geodesic space. Next we recall the definition of uniform spaces from the work of Bonk et al. [Reference Bonk, Heinonen and Koskela2] and use this to establish their bounded uniformization theory of Gromov hyperbolic spaces. For more backgrounds, we refer to [Reference Herron, Shanmugalingam and Xie10, Reference Vuorinen and Zhang23, Reference Zhou, Li and Rasila27] and the references therein.
Definition 3.2. Let ![]() $A\geq 1$. The space
$A\geq 1$. The space ![]() $(\Omega, d)$ is called A-uniform if each pair of points x and y in Ω can be connected with a rectifiable arc α in Ω satisfying:
$(\Omega, d)$ is called A-uniform if each pair of points x and y in Ω can be connected with a rectifiable arc α in Ω satisfying:
(1)
 $\ell(\alpha)\leq A\,d(x,y)$, and
$\ell(\alpha)\leq A\,d(x,y)$, and(2)
 $\min\{\ell(\alpha[x,z]),\ell(\alpha[z,y])\}\leq A\,d(z)$ for all
$\min\{\ell(\alpha[x,z]),\ell(\alpha[z,y])\}\leq A\,d(z)$ for all  $z\in \alpha$,
$z\in \alpha$,
where ![]() $\ell(\alpha)$ is the length of α and
$\ell(\alpha)$ is the length of α and ![]() $\alpha[x,z]$ is the part of α between x and z.
$\alpha[x,z]$ is the part of α between x and z.
3.2. Unbounded uniformization of Gromov hyperbolic spaces
In this subsection, we assume that (X, d) is a proper geodesic space that is δ-hyperbolic, and ![]() $\partial_\infty X$ contains at least two points. Let
$\partial_\infty X$ contains at least two points. Let ![]() $o\in X$,
$o\in X$, ![]() $\xi\in\partial_\infty X$ and
$\xi\in\partial_\infty X$ and ![]() $b=b_{\xi,o}\colon X\to \mathbb{R}$ a Busemann function based at ξ.
$b=b_{\xi,o}\colon X\to \mathbb{R}$ a Busemann function based at ξ.
Following the notation of [Reference Zhou, Ponnusamy and Rasila29], consider the family of conformal deformations of X induced by the densities
 \begin{equation*}
\rho_\varepsilon(x)=\mathrm{e}^{-\varepsilon b(x)} ~\mbox{for }\varepsilon \gt 0.
\end{equation*}
\begin{equation*}
\rho_\varepsilon(x)=\mathrm{e}^{-\varepsilon b(x)} ~\mbox{for }\varepsilon \gt 0.
\end{equation*} The resulting spaces are denoted by ![]() $X_\varepsilon=(X,d_\varepsilon)$. One observes that dɛ is a metric on X defined by
$X_\varepsilon=(X,d_\varepsilon)$. One observes that dɛ is a metric on X defined by
 \begin{equation}
d_\varepsilon(x,y)=\inf_\alpha \int_\alpha \rho_\varepsilon \;ds,
\end{equation}
\begin{equation}
d_\varepsilon(x,y)=\inf_\alpha \int_\alpha \rho_\varepsilon \;ds,
\end{equation} where the infimum is taken over all rectifiable curves α in (X, d) joining the points x and y. The metric completion and the boundary of Xɛ are denoted by ![]() $\overline{X_\varepsilon}$ and
$\overline{X_\varepsilon}$ and ![]() $\partial_\varepsilon X:=\partial X_\varepsilon=\overline{X_\varepsilon}\setminus X_\varepsilon,$ respectively. Let kɛ be the quasihyperbolic metric of
$\partial_\varepsilon X:=\partial X_\varepsilon=\overline{X_\varepsilon}\setminus X_\varepsilon,$ respectively. Let kɛ be the quasihyperbolic metric of ![]() $(X,d_\varepsilon)$.
$(X,d_\varepsilon)$.
Now, we recall certain auxiliary results from [Reference Zhou, Ponnusamy and Rasila29] for later use.
Lemma 3.4. ![]() $($[Reference Zhou, Ponnusamy and Rasila29, Theorem 1.2]
$($[Reference Zhou, Ponnusamy and Rasila29, Theorem 1.2]![]() $)$ For all
$)$ For all ![]() $0 \lt \varepsilon\leq \varepsilon_0(\delta)$, the conformal deformations
$0 \lt \varepsilon\leq \varepsilon_0(\delta)$, the conformal deformations ![]() $X_\varepsilon=(X,d_\varepsilon)$ of X are unbounded A-uniform spaces with a constant
$X_\varepsilon=(X,d_\varepsilon)$ of X are unbounded A-uniform spaces with a constant ![]() $A=A(\delta)$.
$A=A(\delta)$.
Lemma 3.5. ![]() $($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.1]
$($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.1]![]() $)$ There is a constant
$)$ There is a constant ![]() $A_1=A_1(\delta)\geq 1$ such that
$A_1=A_1(\delta)\geq 1$ such that
 \begin{equation*}\frac{1}{A_1} d_\varepsilon (x,y)\leq
\frac{1}{\varepsilon} \mathrm{e}^{-\varepsilon (x|y)_b}\big(\min\{1,\varepsilon d(x,y)\}\big)\leq A_1 d_\varepsilon (x,y),\end{equation*}
\begin{equation*}\frac{1}{A_1} d_\varepsilon (x,y)\leq
\frac{1}{\varepsilon} \mathrm{e}^{-\varepsilon (x|y)_b}\big(\min\{1,\varepsilon d(x,y)\}\big)\leq A_1 d_\varepsilon (x,y),\end{equation*} for all ![]() $x,y\in X$.
$x,y\in X$.
Lemma 3.6. ![]() $($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.5]
$($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.5]![]() $)$ There is a natural bijective map
$)$ There is a natural bijective map ![]() $\phi\colon \partial_\infty X\to \partial_\varepsilon X\cup\{\infty\}$ with
$\phi\colon \partial_\infty X\to \partial_\varepsilon X\cup\{\infty\}$ with ![]() $\phi(\xi)=\infty.$
$\phi(\xi)=\infty.$
Lemma 3.7. ![]() $($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.24]
$($[Reference Zhou, Ponnusamy and Rasila29, Lemma 5.24]![]() $)$ If X is K-roughly starlike with respect to
$)$ If X is K-roughly starlike with respect to ![]() $\xi\in\partial_\infty X$, then for
$\xi\in\partial_\infty X$, then for ![]() $0 \lt \varepsilon\leq \varepsilon_0(\delta)$, the identity map
$0 \lt \varepsilon\leq \varepsilon_0(\delta)$, the identity map ![]() $(X,d)\to (X_\varepsilon,k_\varepsilon)$ is M-bilipschitz with
$(X,d)\to (X_\varepsilon,k_\varepsilon)$ is M-bilipschitz with ![]() $M=M(\delta,K,\varepsilon)$.
$M=M(\delta,K,\varepsilon)$.
3.3. Proof of Theorem 1.1
Let ![]() $\delta,K,\mu\geq 0$ and
$\delta,K,\mu\geq 0$ and ![]() $C,\lambda\geq 1$. Suppose that (X, d) is a proper geodesic space that is δ-hyperbolic and K-roughly starlike with respect to
$C,\lambda\geq 1$. Suppose that (X, d) is a proper geodesic space that is δ-hyperbolic and K-roughly starlike with respect to ![]() $\xi\in \partial_\infty X$. Let
$\xi\in \partial_\infty X$. Let ![]() $\partial_{\infty}X$ be a C-uniformly perfect set. Recall that
$\partial_{\infty}X$ be a C-uniformly perfect set. Recall that
 \begin{equation*}\mathcal{T}_{\lambda,\mu}(X^*) =\big \{f:\,X^*\rightarrow X^*\;\big|\; f|_X\;
\mbox{is a } (\lambda,\mu) \mbox{-quasi-isometry and }~ f|_{\partial_\infty X}={\text{id}}_{\partial_{\infty}X} \big \}.
\end{equation*}
\begin{equation*}\mathcal{T}_{\lambda,\mu}(X^*) =\big \{f:\,X^*\rightarrow X^*\;\big|\; f|_X\;
\mbox{is a } (\lambda,\mu) \mbox{-quasi-isometry and }~ f|_{\partial_\infty X}={\text{id}}_{\partial_{\infty}X} \big \}.
\end{equation*}The issue is to find a constant Λ such that
for each ![]() $f\in \mathcal{T}_{\lambda,\mu}(X^*)$ and for all
$f\in \mathcal{T}_{\lambda,\mu}(X^*)$ and for all ![]() $x\in X$.
$x\in X$.
Let ![]() $b=b_{\xi,o}\colon X\to \mathbb{R}$ be a Busemann function based at ξ with
$b=b_{\xi,o}\colon X\to \mathbb{R}$ be a Busemann function based at ξ with ![]() $o\in X$. Fix a constant
$o\in X$. Fix a constant ![]() $\varepsilon=\varepsilon(\delta, K)$. Let
$\varepsilon=\varepsilon(\delta, K)$. Let ![]() $X_{\varepsilon}:=(X, d_{\varepsilon})$ be the uniformization of (X, d) induced by the conformal deformation as in Equation (3.3).
$X_{\varepsilon}:=(X, d_{\varepsilon})$ be the uniformization of (X, d) induced by the conformal deformation as in Equation (3.3).
One observes from Lemma 3.4 that Xɛ is unbounded and A-uniform with ![]() $A=A(\delta)$. According to Lemma 3.5, we know that
$A=A(\delta)$. According to Lemma 3.5, we know that
is actually a bilipschitz map, where ![]() $d_{b,\varepsilon}$ is a Hamenstädt metric based at ξ with parameter ɛ. Because (X, d) is K-roughly starlike with respect to
$d_{b,\varepsilon}$ is a Hamenstädt metric based at ξ with parameter ɛ. Because (X, d) is K-roughly starlike with respect to ![]() $\xi\in \partial_\infty X$, it follows from Lemma 3.7 that the identity map
$\xi\in \partial_\infty X$, it follows from Lemma 3.7 that the identity map
is M-bilipschitz with ![]() $M=M(\delta, K,\varepsilon)$.
$M=M(\delta, K,\varepsilon)$.
Thanks to [Reference Wang and Zhou24, Theorem C], we see that the uniform perfectness is preserved under quasimöbius maps; for the definition of quasimöbius maps, see [Reference Väisälä20]. It follows from [Reference Buyalo and Schroeder5, Theorem 5.2.17] that ![]() $\partial_\infty X$ equipped with any two visual metrics or Hamenstädt metrics are quasimöbius equivalent to each other with the control function depending only on δ. As
$\partial_\infty X$ equipped with any two visual metrics or Hamenstädt metrics are quasimöbius equivalent to each other with the control function depending only on δ. As ![]() $\partial_\infty X$ is C-uniformly perfect with respect to a certain visual metric, one thus finds that
$\partial_\infty X$ is C-uniformly perfect with respect to a certain visual metric, one thus finds that ![]() $\partial_\varepsilon X$ is C 0-uniformly perfect with
$\partial_\varepsilon X$ is C 0-uniformly perfect with ![]() $C_0=C_0(C, \delta)$.
$C_0=C_0(C, \delta)$.
Fix ![]() $f\in \mathcal{T}_{\lambda,\mu}(X^*)$. We observe that f induces a map
$f\in \mathcal{T}_{\lambda,\mu}(X^*)$. We observe that f induces a map ![]() $g\colon \overline{X_\varepsilon } \cup \{\infty\}\to \overline{X_\varepsilon }\cup \{\infty\}$ with
$g\colon \overline{X_\varepsilon } \cup \{\infty\}\to \overline{X_\varepsilon }\cup \{\infty\}$ with
and
Next, we show that the following three items:
(1)
 $g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$;
$g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$;(2) The continuous extension of g from Xɛ to the one-point extended boundary
 $\partial_\varepsilon X\cup \{\infty\}$ is exactly
$\partial_\varepsilon X\cup \{\infty\}$ is exactly  $g|_{\partial_\varepsilon X\cup\{\infty\}}$;
$g|_{\partial_\varepsilon X\cup\{\infty\}}$;(3) There is a homeomorphism
 $\eta_0\colon [0,\infty)\to [0,\infty)$ such that
(3.8)
$\eta_0\colon [0,\infty)\to [0,\infty)$ such that
(3.8) \begin{equation}
\frac{d_\varepsilon(g(x),g(a))}{d_\varepsilon(g(y),g(a))}\leq \eta_0\left(\frac{d_\varepsilon(x,a)}{d_\varepsilon(y,a)}\right),
\end{equation}
\begin{equation}
\frac{d_\varepsilon(g(x),g(a))}{d_\varepsilon(g(y),g(a))}\leq \eta_0\left(\frac{d_\varepsilon(x,a)}{d_\varepsilon(y,a)}\right),
\end{equation}for all three distinct points
 $x,y\in \overline{X_\varepsilon}$ and
$x,y\in \overline{X_\varepsilon}$ and  $a\in \partial_\varepsilon X$.
$a\in \partial_\varepsilon X$.
Because ![]() $f\in \mathcal{T}_{\lambda,\mu}(X^*)$, we have
$f\in \mathcal{T}_{\lambda,\mu}(X^*)$, we have ![]() $f|_{\partial_\infty X}={\text{id}}_{\partial_\infty X}$ and this proves (1).
$f|_{\partial_\infty X}={\text{id}}_{\partial_\infty X}$ and this proves (1).
To prove (2), for each sequence ![]() $\{x_n\}$ which is dɛ-convergent to
$\{x_n\}$ which is dɛ-convergent to ![]() $a\in \partial_\varepsilon X\cup \{\infty\}$, we check that the sequence
$a\in \partial_\varepsilon X\cup \{\infty\}$, we check that the sequence ![]() $\{g(x_n)\}=\{f(x_n)\}$ is dɛ-convergent to
$\{g(x_n)\}=\{f(x_n)\}$ is dɛ-convergent to ![]() $g(a)=a$. By Lemma 3.6, one observes that
$g(a)=a$. By Lemma 3.6, one observes that ![]() $\{x_n\}$ is a Gromov sequence of X such that
$\{x_n\}$ is a Gromov sequence of X such that ![]() $\{x_n\}\in \phi^{-1}(a)\in \partial_\infty X$. As
$\{x_n\}\in \phi^{-1}(a)\in \partial_\infty X$. As ![]() $f\colon X\to X$ is a quasi-isometry which has a continuous extension to
$f\colon X\to X$ is a quasi-isometry which has a continuous extension to ![]() $\partial_\infty X$ such that
$\partial_\infty X$ such that ![]() $f|_{\partial_\infty X}={\text{id}}_{\partial_\infty X}$, we see from [Reference Bonk and Schramm3, Proposition 6.3] that
$f|_{\partial_\infty X}={\text{id}}_{\partial_\infty X}$, we see from [Reference Bonk and Schramm3, Proposition 6.3] that ![]() $\{f(x_n)\}$ is also a Gromov sequence of X satisfying
$\{f(x_n)\}$ is also a Gromov sequence of X satisfying
Then Lemma 3.6 guarantees that ![]() $\{f(x_n)\}$ is dɛ-convergent to
$\{f(x_n)\}$ is dɛ-convergent to ![]() $\phi[\phi^{-1}(a)]=a=g(a)\in \partial_\varepsilon X\cup \{\infty\}$, as desired.
$\phi[\phi^{-1}(a)]=a=g(a)\in \partial_\varepsilon X\cup \{\infty\}$, as desired.
It remains to show the last item (3). For any given three distinct points ![]() $x,y\in \overline{X_\varepsilon}$ and
$x,y\in \overline{X_\varepsilon}$ and ![]() $a\in \partial_\varepsilon X$, we let
$a\in \partial_\varepsilon X$, we let
Choose sequences ![]() $\{x_n\}$,
$\{x_n\}$, ![]() $\{y_n\}$ and
$\{y_n\}$ and ![]() $\{a_n\}$ in X so that they are dɛ-convergent to
$\{a_n\}$ in X so that they are dɛ-convergent to ![]() $x, y$ and a, respectively. From the statement (2), it follows that
$x, y$ and a, respectively. From the statement (2), it follows that ![]() $\{g(x_n)\}$,
$\{g(x_n)\}$, ![]() $\{g(y_n)\}$ and
$\{g(y_n)\}$ and ![]() $\{g(a_n)\}$ are dɛ-convergent to g(x), g(y) and g(a), respectively. Moreover, by Lemma 3.6, we have
$\{g(a_n)\}$ are dɛ-convergent to g(x), g(y) and g(a), respectively. Moreover, by Lemma 3.6, we have ![]() $\{a_n\}\in \phi^{-1}(a)\in\partial_\infty X$ and
$\{a_n\}\in \phi^{-1}(a)\in\partial_\infty X$ and ![]() $\phi^{-1}(x)\neq \phi^{-1}(a)\neq \phi^{-1}(y)$, because
$\phi^{-1}(x)\neq \phi^{-1}(a)\neq \phi^{-1}(y)$, because ![]() $x\neq a\neq y$. Without loss of generality, we may assume that for all n,
$x\neq a\neq y$. Without loss of generality, we may assume that for all n,
 \begin{equation*}
\min\Big\{d(x_n,a_n), \;d(y_n,a_n), \;d(f(x_n),f(a_n)), \;d(f(y_n),f(a_n))\Big\}\geq 1.
\end{equation*}
\begin{equation*}
\min\Big\{d(x_n,a_n), \;d(y_n,a_n), \;d(f(x_n),f(a_n)), \;d(f(y_n),f(a_n))\Big\}\geq 1.
\end{equation*} By Lemma 3.5, there is a constant ![]() $A_1=A_1(\delta)\geq 1$ such that
$A_1=A_1(\delta)\geq 1$ such that
 \begin{eqnarray*}
t_n =\frac{d_\varepsilon(x_n,a_n)}{d_\varepsilon(y_n,a_n)} & \geq & \frac{1}{A_1^2} \mathrm{e}^{\varepsilon (y_n|a_n)_b- \varepsilon (x_n|a_n)_b}\frac{\min\{1, [\varepsilon d(x_n,a_n)]\}}{\min\{1, [\varepsilon d(y_n,a_n)]\}} \\ & = & \frac{1}{A_1^2} \mathrm{e}^{\varepsilon (y_n|a_n)_b- \varepsilon (x_n|a_n)_b}.
\end{eqnarray*}
\begin{eqnarray*}
t_n =\frac{d_\varepsilon(x_n,a_n)}{d_\varepsilon(y_n,a_n)} & \geq & \frac{1}{A_1^2} \mathrm{e}^{\varepsilon (y_n|a_n)_b- \varepsilon (x_n|a_n)_b}\frac{\min\{1, [\varepsilon d(x_n,a_n)]\}}{\min\{1, [\varepsilon d(y_n,a_n)]\}} \\ & = & \frac{1}{A_1^2} \mathrm{e}^{\varepsilon (y_n|a_n)_b- \varepsilon (x_n|a_n)_b}.
\end{eqnarray*}This ensures that
 \begin{equation}
(y_n|a_n)_b-(x_n|a_n)_b \leq A_2+ \frac{1}{\varepsilon}\log t_n
\end{equation}
\begin{equation}
(y_n|a_n)_b-(x_n|a_n)_b \leq A_2+ \frac{1}{\varepsilon}\log t_n
\end{equation} with ![]() $A_2=2(\log A_1)/\varepsilon$.
$A_2=2(\log A_1)/\varepsilon$.
By a similar argument as above, we see from Lemma 3.5 that
 \begin{eqnarray}
T_n=\frac{d_\varepsilon(g(x_n),g(a_n))}{d_\varepsilon(g(y_n),g(a_n))}&=&\frac{d_\varepsilon
(f(x_n),f(a_n))}{d_\varepsilon(f(y_n),f(a_n))}\\ \nonumber
\end{eqnarray}
\begin{eqnarray}
T_n=\frac{d_\varepsilon(g(x_n),g(a_n))}{d_\varepsilon(g(y_n),g(a_n))}&=&\frac{d_\varepsilon
(f(x_n),f(a_n))}{d_\varepsilon(f(y_n),f(a_n))}\\ \nonumber
\end{eqnarray} \begin{eqnarray*}
&\leq & A_1^2 e^{\varepsilon (f(y_n)|f(a_n))_b- \varepsilon (f(x_n)|f(a_n))_b}.
\end{eqnarray*}
\begin{eqnarray*}
&\leq & A_1^2 e^{\varepsilon (f(y_n)|f(a_n))_b- \varepsilon (f(x_n)|f(a_n))_b}.
\end{eqnarray*} On the other hand, we note that ![]() $b\in \mathcal{B}(\xi)$ and
$b\in \mathcal{B}(\xi)$ and ![]() $f(\xi)=\xi$. As
$f(\xi)=\xi$. As ![]() $f\colon (X,d)\to (X,d)$ is a
$f\colon (X,d)\to (X,d)$ is a ![]() $(\lambda,\mu)$-quasi-isometry, it follows from [Reference Zhou, Ponnusamy and Rasila29, Lemma 3.7] that there exists a control function
$(\lambda,\mu)$-quasi-isometry, it follows from [Reference Zhou, Ponnusamy and Rasila29, Lemma 3.7] that there exists a control function ![]() $\theta\colon \mathbb{R}\to \mathbb{R}$ depending only on
$\theta\colon \mathbb{R}\to \mathbb{R}$ depending only on ![]() $\lambda, \mu$ and δ with
$\lambda, \mu$ and δ with
such that
This, together with Equations (3.10) and (3.9), implies that
 \begin{equation}
T_n\leq A_1^2 \mathrm{e}^{\varepsilon \theta\big(\frac{1}{\varepsilon}\log t_n\big)}.
\end{equation}
\begin{equation}
T_n\leq A_1^2 \mathrm{e}^{\varepsilon \theta\big(\frac{1}{\varepsilon}\log t_n\big)}.
\end{equation} Again by Lemma 3.6, we see that ![]() $T_n\to T$ and
$T_n\to T$ and ![]() $t_n\to t$ as
$t_n\to t$ as ![]() $n\to \infty$. Therefore, we obtain Equation (3.8) from Equation (3.11) by letting
$n\to \infty$. Therefore, we obtain Equation (3.8) from Equation (3.11) by letting ![]() $n\to \infty$. This ensures (3).
$n\to \infty$. This ensures (3).
We continue the proof of this theorem. Fix ![]() $x\in X$, and choose a point
$x\in X$, and choose a point ![]() $x_0\in \partial_\varepsilon X$ such that
$x_0\in \partial_\varepsilon X$ such that ![]() $d_\varepsilon(x,x_0)=d_\varepsilon (x)={\text{dist}}_\varepsilon(x,\partial_\varepsilon X).$ We wish to obtain an upper bound for the quasihyperbolic distance kɛ between x and
$d_\varepsilon(x,x_0)=d_\varepsilon (x)={\text{dist}}_\varepsilon(x,\partial_\varepsilon X).$ We wish to obtain an upper bound for the quasihyperbolic distance kɛ between x and ![]() $g(x)=f(x)$. To this end, we first show the following:
$g(x)=f(x)$. To this end, we first show the following:
Claim. There is a constant ![]() $M_1\geq 1$ such that
$M_1\geq 1$ such that
 \begin{equation*}\frac{d_\varepsilon(x)}{M_1}\leq d_\varepsilon (g(x)) \leq d_\varepsilon(g(x),g(x_0)) \leq M_1 d_\varepsilon(x).\end{equation*}
\begin{equation*}\frac{d_\varepsilon(x)}{M_1}\leq d_\varepsilon (g(x)) \leq d_\varepsilon(g(x),g(x_0)) \leq M_1 d_\varepsilon(x).\end{equation*} We first check that ![]() $d_\varepsilon(g(x),g(x_0)) \leq M_0 d_\varepsilon(x)$ for some
$d_\varepsilon(g(x),g(x_0)) \leq M_0 d_\varepsilon(x)$ for some ![]() $M_0\geq 1$. As
$M_0\geq 1$. As ![]() $\partial_\varepsilon X$ is unbounded, it is clear that
$\partial_\varepsilon X$ is unbounded, it is clear that ![]() $\partial_\varepsilon X \setminus B_\varepsilon(x_0, d_\varepsilon(x))\neq \emptyset$. Thus there is a point
$\partial_\varepsilon X \setminus B_\varepsilon(x_0, d_\varepsilon(x))\neq \emptyset$. Thus there is a point ![]() $x_1\in \partial_\varepsilon X$ such that
$x_1\in \partial_\varepsilon X$ such that
 \begin{equation}
\frac{d_\varepsilon(x)}{C_0}\leq d_\varepsilon(x_0,x_1) \leq d_\varepsilon(x),
\end{equation}
\begin{equation}
\frac{d_\varepsilon(x)}{C_0}\leq d_\varepsilon(x_0,x_1) \leq d_\varepsilon(x),
\end{equation} because ![]() $\partial_\varepsilon X$ is C 0-uniformly perfect. Note that
$\partial_\varepsilon X$ is C 0-uniformly perfect. Note that ![]() $g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$. Now, by Equations (3.8) and (3.12), we obtain
$g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$. Now, by Equations (3.8) and (3.12), we obtain
 \begin{eqnarray*}
d_\varepsilon(g(x),g(x_0)) & \leq & \eta_0\left (\frac{d_\varepsilon (x,x_0)}{d_\varepsilon (x_1,x_0)}\right) d_\varepsilon(g(x_1),g(x_0))
\\ & \leq & \eta_0(C_0) d_\varepsilon(x_1,x_0)
\\ & \leq & \eta_0(C_0) d_\varepsilon(x)=M_0 d_\varepsilon(x).
\end{eqnarray*}
\begin{eqnarray*}
d_\varepsilon(g(x),g(x_0)) & \leq & \eta_0\left (\frac{d_\varepsilon (x,x_0)}{d_\varepsilon (x_1,x_0)}\right) d_\varepsilon(g(x_1),g(x_0))
\\ & \leq & \eta_0(C_0) d_\varepsilon(x_1,x_0)
\\ & \leq & \eta_0(C_0) d_\varepsilon(x)=M_0 d_\varepsilon(x).
\end{eqnarray*} For the other direction, by an elementary computation, we see from Equation (3.8) that for any three distinct points ![]() $x,y\in \overline{X_\varepsilon}$ and
$x,y\in \overline{X_\varepsilon}$ and ![]() $a\in \partial_\varepsilon X$,
$a\in \partial_\varepsilon X$,
 \begin{equation}
\frac{d_\varepsilon(x,a)}{d_\varepsilon(y,a)} \leq \eta_1\left (\frac{d_\varepsilon(g(x),g(a))}{d_\varepsilon(g(y),g(a))}\right),
\end{equation}
\begin{equation}
\frac{d_\varepsilon(x,a)}{d_\varepsilon(y,a)} \leq \eta_1\left (\frac{d_\varepsilon(g(x),g(a))}{d_\varepsilon(g(y),g(a))}\right),
\end{equation} where ![]() $\eta_1=[\eta_0^{-1}(t^{-1})]^{-1}$ for all t > 0.
$\eta_1=[\eta_0^{-1}(t^{-1})]^{-1}$ for all t > 0.
Thus by Equation (3.13), a similar argument as above guarantees that
for some constant ![]() $M_1 \,(\geq M_0)$ depending only on η 0 and C 0. Therefore, the claim is proved.
$M_1 \,(\geq M_0)$ depending only on η 0 and C 0. Therefore, the claim is proved.
Finally, we are ready to complete the proof of Theorem 1.1. Because ![]() $g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$, we see from the claim that
$g|_{\partial_\varepsilon X}={\text{id}}_{\partial_\varepsilon X}$, we see from the claim that
 \begin{equation}
\begin{aligned}
d_\varepsilon(g(x),x) & \leq d_\varepsilon(x_0,x) + d_\varepsilon(g(x),g(x_0))\\
& \leq d_\varepsilon(x)+M_1 d_\varepsilon(x)\\
& \leq M_1(M_1+1) \min\{d_\varepsilon(x), d_\varepsilon(g(x))\}.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
d_\varepsilon(g(x),x) & \leq d_\varepsilon(x_0,x) + d_\varepsilon(g(x),g(x_0))\\
& \leq d_\varepsilon(x)+M_1 d_\varepsilon(x)\\
& \leq M_1(M_1+1) \min\{d_\varepsilon(x), d_\varepsilon(g(x))\}.
\end{aligned}
\end{equation} Moreover, because ![]() $(X,d_\varepsilon)$ is A-uniform, it follows from Equation (3.14) and [Reference Bonk, Heinonen and Koskela2, Lemma 2.13] that
$(X,d_\varepsilon)$ is A-uniform, it follows from Equation (3.14) and [Reference Bonk, Heinonen and Koskela2, Lemma 2.13] that
 \begin{eqnarray*}
k_\varepsilon(x,g(x)) & \leq & 4A^2\log \left(1+\frac{d_\varepsilon(g(x),x)}{\min\{d_\varepsilon(x), d_\varepsilon(g(x))\}}\right)
\\ & \leq & 4A^2 \log \big (1+M_1(M_1+1)\big).
\end{eqnarray*}
\begin{eqnarray*}
k_\varepsilon(x,g(x)) & \leq & 4A^2\log \left(1+\frac{d_\varepsilon(g(x),x)}{\min\{d_\varepsilon(x), d_\varepsilon(g(x))\}}\right)
\\ & \leq & 4A^2 \log \big (1+M_1(M_1+1)\big).
\end{eqnarray*} Because the identity map ![]() $\varphi\colon (X, d) \to (X_\varepsilon, k_\varepsilon)$ is M-bilipschitz, we obtain
$\varphi\colon (X, d) \to (X_\varepsilon, k_\varepsilon)$ is M-bilipschitz, we obtain
finishing the proof.
4. Examples and applications
4.1. Examples
While studying the Teichmüller displacement problem on Gromov hyperbolic spaces X that is roughly starlike with respect to an interior point ![]() $w\in X$, one observes from Corollary 1.5 that the upper bound for the displacement depends on the diameter of
$w\in X$, one observes from Corollary 1.5 that the upper bound for the displacement depends on the diameter of ![]() $(\partial_\infty X, d_{w,\varepsilon})$. In the following, we provide two examples to explain this phenomenon.
$(\partial_\infty X, d_{w,\varepsilon})$. In the following, we provide two examples to explain this phenomenon.
Example 4.1. Let ![]() $\mathbb{H}^2$ be the Poincaré hyperbolic disk with the original point
$\mathbb{H}^2$ be the Poincaré hyperbolic disk with the original point ![]() $o\in \mathbb{H}^2$. For a given integer
$o\in \mathbb{H}^2$. For a given integer ![]() $m\geq 1$, we attach
$m\geq 1$, we attach ![]() $\mathbb{H}^2$ at the point o with a line segment
$\mathbb{H}^2$ at the point o with a line segment ![]() $I_m=\{o\times [0,m]\}$. We define the space
$I_m=\{o\times [0,m]\}$. We define the space ![]() $Y=\mathbb{H}^2\sqcup I_m$ equipped with the induced length metric d. Then we have the following:
$Y=\mathbb{H}^2\sqcup I_m$ equipped with the induced length metric d. Then we have the following:
(1) Clearly, (Y, d) is a Gromov hyperbolic metric space that is 0-roughly starlike with respect to
 $w=(o,m)$. The Gromov boundary
$w=(o,m)$. The Gromov boundary  $\partial_\infty Y$ is the same as
$\partial_\infty Y$ is the same as  $\partial_\infty \mathbb{H}^2=\mathbb{S}^1$, which is connected and therefore uniformly perfect.
$\partial_\infty \mathbb{H}^2=\mathbb{S}^1$, which is connected and therefore uniformly perfect.(2) One easily finds that the diameter of
 $(\partial_\infty Y, d_{w,\varepsilon})$ is comparable with
$(\partial_\infty Y, d_{w,\varepsilon})$ is comparable with  $e^{-m \varepsilon}$.
$e^{-m \varepsilon}$.(3) We define a mapping
 $f\colon Y\to Y$ such that
$f\colon Y\to Y$ such that  $f|_{\mathbb{H}^2}={\text{id}}_{\mathbb{H}^2}$ and
$f|_{\mathbb{H}^2}={\text{id}}_{\mathbb{H}^2}$ and  $f|_{I_m}$ is a linear function with
$f|_{I_m}$ is a linear function with  $f(u)=(o,m/4)$, where
$f(u)=(o,m/4)$, where  $u=(o,m/2)\in Y$. It is not hard to see that f is a
$u=(o,m/2)\in Y$. It is not hard to see that f is a  $(4,0)$-quasi-isometry which induces a boundary map
$(4,0)$-quasi-isometry which induces a boundary map  $f|_{\partial_\infty Y}={\text{id}}_{\partial_{\infty} Y}$. However,
$f|_{\partial_\infty Y}={\text{id}}_{\partial_{\infty} Y}$. However,  $d(u,f(u))=m/4$.
$d(u,f(u))=m/4$.
The second example tells us that the Teichmüller displacement theorem for quasiconformal mappings, namely [Reference Vuorinen and Zhang23, Theorem 1.9] and [Reference Zhou and Rasila30, Theorem 1.2], is not valid for domains G in the Riemann spheres, where the displacement depends also on the diameter of ![]() $\partial G$ with respect to the spherical metric.
$\partial G$ with respect to the spherical metric.
Example 4.2. Let ![]() $\mathbb{\overline{R}}^2=\mathbb{R}^2\cup\{\infty\}$ be the Riemann 2-sphere, and
$\mathbb{\overline{R}}^2=\mathbb{R}^2\cup\{\infty\}$ be the Riemann 2-sphere, and ![]() $|\cdot|$ the Euclidean metric on
$|\cdot|$ the Euclidean metric on ![]() $\mathbb{R}^2$. Let
$\mathbb{R}^2$. Let ![]() $0 \lt \epsilon\leq 1/4$,
$0 \lt \epsilon\leq 1/4$, ![]() $\overline{B}(0,\epsilon)=\{z\in \mathbb{R}^2|\;|z|\leq \epsilon \}$, and
$\overline{B}(0,\epsilon)=\{z\in \mathbb{R}^2|\;|z|\leq \epsilon \}$, and ![]() $D_\epsilon= \mathbb{\overline{R}}^2\setminus \overline{B}(0,\epsilon)$. Define
$D_\epsilon= \mathbb{\overline{R}}^2\setminus \overline{B}(0,\epsilon)$. Define ![]() $g\colon D_\epsilon\to D_\epsilon$ with
$g\colon D_\epsilon\to D_\epsilon$ with ![]() $g(\infty)=\infty$ and
$g(\infty)=\infty$ and
 \begin{equation*}
g(z)=\frac{1}{\epsilon}|z|z ~\mbox{for all } z\in D_\epsilon\setminus\{\infty\}.
\end{equation*}
\begin{equation*}
g(z)=\frac{1}{\epsilon}|z|z ~\mbox{for all } z\in D_\epsilon\setminus\{\infty\}.
\end{equation*} Let σ be the spherical metric on ![]() $\mathbb{\overline{R}}^2$ defined as in [Reference Hariri, Klén and Vuorinen8, (3.6)]. Then we have the following:
$\mathbb{\overline{R}}^2$ defined as in [Reference Hariri, Klén and Vuorinen8, (3.6)]. Then we have the following:
(1)
 $(D_\epsilon,\sigma)$ is a bounded locally compact uniform metric space with
$(D_\epsilon,\sigma)$ is a bounded locally compact uniform metric space with
 \begin{equation*}{\text{diam}}_\sigma(\partial D_\epsilon)=\frac{2\epsilon}{1+\epsilon^2}.\end{equation*}
\begin{equation*}{\text{diam}}_\sigma(\partial D_\epsilon)=\frac{2\epsilon}{1+\epsilon^2}.\end{equation*}(2) Let
 $k_{D_\epsilon}(\sigma)$ be the quasihyperbolic metric of
$k_{D_\epsilon}(\sigma)$ be the quasihyperbolic metric of  $(D_\epsilon,\sigma)$, see Definition 3.1. It follows from [Reference Bonk, Heinonen and Koskela2, Theorem 3.6] that
$(D_\epsilon,\sigma)$, see Definition 3.1. It follows from [Reference Bonk, Heinonen and Koskela2, Theorem 3.6] that  $(D_\epsilon,k_{D_\epsilon}(\sigma))$ is a proper geodesic Gromov hyperbolic space that is roughly starlike with respect to a point
$(D_\epsilon,k_{D_\epsilon}(\sigma))$ is a proper geodesic Gromov hyperbolic space that is roughly starlike with respect to a point  $w\in D_\epsilon$. Moreover, there is a natural quasisymmetric homeomorphism between the metric boundary
$w\in D_\epsilon$. Moreover, there is a natural quasisymmetric homeomorphism between the metric boundary  $(\partial D_\epsilon,\sigma)$ and the Gromov boundary
$(\partial D_\epsilon,\sigma)$ and the Gromov boundary  $\partial_\infty D_\epsilon$ of
$\partial_\infty D_\epsilon$ of  $(D_\epsilon,k_{D_\epsilon}(\sigma))$ endowed with a visual metric.
$(D_\epsilon,k_{D_\epsilon}(\sigma))$ endowed with a visual metric.(3) The mapping
 $g\colon (D_\epsilon,\sigma)\to (D_\epsilon,\sigma)$ is quasiconformal and has a continuous extension to
$g\colon (D_\epsilon,\sigma)\to (D_\epsilon,\sigma)$ is quasiconformal and has a continuous extension to  $\partial D_\epsilon$ with
$\partial D_\epsilon$ with  $g|_{\partial D_\epsilon}={\text{id}}_{\partial D_\epsilon}$. Hence
$g|_{\partial D_\epsilon}={\text{id}}_{\partial D_\epsilon}$. Hence  $g\colon (D_\epsilon,k_{D_\epsilon}(\sigma))\to (D_\epsilon,k_{D_\epsilon}(\sigma))$ is a quasi-isometry and has a continuous extension to
$g\colon (D_\epsilon,k_{D_\epsilon}(\sigma))\to (D_\epsilon,k_{D_\epsilon}(\sigma))$ is a quasi-isometry and has a continuous extension to  $\partial_\infty D_\epsilon$ which is the identity map on
$\partial_\infty D_\epsilon$ which is the identity map on  $\partial_\infty D_\epsilon$.
$\partial_\infty D_\epsilon$.(4) Clearly,
 $\partial D_\epsilon$ is connected and so is
$\partial D_\epsilon$ is connected and so is  $\partial_\infty D_\epsilon$. In particular,
$\partial_\infty D_\epsilon$. In particular,  $\partial_\infty D_\epsilon$ is uniformly perfect. Therefore, we know from Corollary 1.5 that the displacement
$\partial_\infty D_\epsilon$ is uniformly perfect. Therefore, we know from Corollary 1.5 that the displacement  $k_{D_\epsilon}(\sigma)(z,g(z))$ is bounded above for all
$k_{D_\epsilon}(\sigma)(z,g(z))$ is bounded above for all  $z\in D_\epsilon$. Note that the upper bound depends on ϵ.
$z\in D_\epsilon$. Note that the upper bound depends on ϵ.(5) As ϵ → 0, one finds that
 ${\text{diam}}_\sigma(\partial D_\epsilon)\to 0$ and
${\text{diam}}_\sigma(\partial D_\epsilon)\to 0$ and
 \begin{equation*}k_{D_\epsilon}(\sigma)\big((\sqrt{\epsilon},0),g((\sqrt{\epsilon},0))\big)\geq \log\left (1+\frac{\sqrt{1+\epsilon^2}}{\sqrt{2}\epsilon}\right)\to \infty.\end{equation*}
\begin{equation*}k_{D_\epsilon}(\sigma)\big((\sqrt{\epsilon},0),g((\sqrt{\epsilon},0))\big)\geq \log\left (1+\frac{\sqrt{1+\epsilon^2}}{\sqrt{2}\epsilon}\right)\to \infty.\end{equation*}
4.2. Applications
This subsection focuses on some applications of Theorem 1.1. Let ![]() $\delta, K\geq 0$,
$\delta, K\geq 0$, ![]() $C\geq 1$ and
$C\geq 1$ and ![]() $\eta\colon [0,\infty)\to [0,\infty)$ be a homeomorphism. Suppose that (X, d) and
$\eta\colon [0,\infty)\to [0,\infty)$ be a homeomorphism. Suppose that (X, d) and ![]() $(X',d')$ are proper geodesic δ-hyperbolic spaces, and
$(X',d')$ are proper geodesic δ-hyperbolic spaces, and ![]() $\partial_\infty X$ is C-uniformly perfect which contains at least two points, and
$\partial_\infty X$ is C-uniformly perfect which contains at least two points, and ![]() $F\colon \partial_\infty X\to \partial_\infty X'$ is η-quasisymmetric with respect to visual metrics. For the definition and properties of quasisymmetric maps, we refer to [Reference Heinonen9, Reference Väisälä20, Reference Wang and Zhou24].
$F\colon \partial_\infty X\to \partial_\infty X'$ is η-quasisymmetric with respect to visual metrics. For the definition and properties of quasisymmetric maps, we refer to [Reference Heinonen9, Reference Väisälä20, Reference Wang and Zhou24].
It is known that if the Gromov boundaries of two roughly starlike hyperbolic geodesic spaces are powerly quasisymmetrically equivalent, then they are quasi-isometrically equivalent (cf. [Reference Bonk and Schramm3, Reference Buyalo and Schroeder5]). As a consequence of Theorem 1.1, we thus obtain that any such two quasi-isometries are bounded above up to a finite distance.
Corollary 4.3. Suppose that X and Xʹ are K-roughly starlike with respect to points on Gromov boundaries, respectively. Then there is a number ![]() $\Lambda_2=\Lambda_2(K,\delta, C,\eta,\lambda,\mu)$ such that, for
$\Lambda_2=\Lambda_2(K,\delta, C,\eta,\lambda,\mu)$ such that, for ![]() $(\lambda,\mu)$-quasi-isometries
$(\lambda,\mu)$-quasi-isometries ![]() $f_1,f_2\colon X\to X'$ induced by F with
$f_1,f_2\colon X\to X'$ induced by F with ![]() ${f_1}|_{\partial_\infty X}={f_2}|_{\partial_\infty X}=F$,
${f_1}|_{\partial_\infty X}={f_2}|_{\partial_\infty X}=F$,
Proof. By [Reference Heinonen9, Exercise 11.2 and Theorem 11.3], we observe that ![]() $\partial_\infty X'$ is Cʹ-uniformly perfect and the inverse of F,
$\partial_\infty X'$ is Cʹ-uniformly perfect and the inverse of F, ![]() $F^{-1}\colon \partial_\infty X'\to \partial_\infty X,$ is a powerly η 1-quasisymmetric map with Cʹ and η 1 depending only on C and η. Note that the visual property and rough starlikeness of a proper geodesic hyperbolic space are equivalent. It follows from [Reference Buyalo and Schroeder5, Corollary 7.2.3] that there is a
$F^{-1}\colon \partial_\infty X'\to \partial_\infty X,$ is a powerly η 1-quasisymmetric map with Cʹ and η 1 depending only on C and η. Note that the visual property and rough starlikeness of a proper geodesic hyperbolic space are equivalent. It follows from [Reference Buyalo and Schroeder5, Corollary 7.2.3] that there is a ![]() $(\lambda_1,\mu_1)$-quasi-isometry
$(\lambda_1,\mu_1)$-quasi-isometry ![]() $g\colon X'\to X$ whose natural extension
$g\colon X'\to X$ whose natural extension  $g|_{\partial_\infty X'}=F^{-1}$, where λ 1 and µ 1 depend only on
$g|_{\partial_\infty X'}=F^{-1}$, where λ 1 and µ 1 depend only on ![]() $\delta,$ K and η 1. As the composition of quasi-isometries is also a quasi-isometry, we immediately find that
$\delta,$ K and η 1. As the composition of quasi-isometries is also a quasi-isometry, we immediately find that
for some positive constants ![]() $\lambda'$ and
$\lambda'$ and ![]() $\mu'$ which depend only on
$\mu'$ which depend only on ![]() $\lambda,\lambda_1,\mu,\mu_1$ and δ.
$\lambda,\lambda_1,\mu,\mu_1$ and δ.
Now by Theorem 1.1, we see that there is a constant ![]() $\Lambda=\Lambda(\lambda',\mu',C',\delta,K)$ such that for all
$\Lambda=\Lambda(\lambda',\mu',C',\delta,K)$ such that for all ![]() $x\in X$,
$x\in X$,
As ![]() $g\colon X'\to X$ is a
$g\colon X'\to X$ is a ![]() $(\lambda_1,\mu_1)$-quasi-isometry, the above two inequalities ensure that
$(\lambda_1,\mu_1)$-quasi-isometry, the above two inequalities ensure that
and the proof of the corollary is complete.
Performing a similar argument as in the proof of Corollary 4.3, we obtain the following result as a consequence of Corollary 1.5.
Corollary 4.4. Suppose that X and Xʹ are K-roughly starlike with respect to ![]() $w\in X$ and
$w\in X$ and ![]() $w'\in X'$ respectively, and
$w'\in X'$ respectively, and ![]() $\vartheta={\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \gt 0$. Then there is a number
$\vartheta={\text{diam}} (\partial_\infty X, d_{w,\varepsilon}) \gt 0$. Then there is a number ![]() $\Lambda_3=\Lambda_3(K,\delta, C,\eta,\lambda,\mu,\vartheta)$ such that, for
$\Lambda_3=\Lambda_3(K,\delta, C,\eta,\lambda,\mu,\vartheta)$ such that, for ![]() $(\lambda,\mu)$-quasi-isometries
$(\lambda,\mu)$-quasi-isometries ![]() $f_1,f_2\colon X\to X'$ induced by F with
$f_1,f_2\colon X\to X'$ induced by F with ![]() ${f_1}|_{\partial_\infty X}={f_2}|_{\partial_\infty X}=F$,
${f_1}|_{\partial_\infty X}={f_2}|_{\partial_\infty X}=F$,
4.3. Concluding remarks
Now, we consider the connection between Theorem 1.1 and the following question proposed by Xie:
Question 4.5.
([Reference Xie25, Question 7.1]) Let Y 1 and Y 2 be two Hadamard n-manifolds (whose sectional curvatures are bounded from below) with n ≠ 4, and ![]() $g\colon Y_1\to Y_2$ a quasi-isometry. Is g always a finite distance from a bilipschitz homeomorphism?
$g\colon Y_1\to Y_2$ a quasi-isometry. Is g always a finite distance from a bilipschitz homeomorphism?
Because the boundary of a Hadamard manifold is homeomorphic to a sphere, it is not hard to see from Corollary 4.3 that whenever one finds a bilipschitz map ![]() $\widetilde{g}\colon Y_1\to Y_2$ with
$\widetilde{g}\colon Y_1\to Y_2$ with ![]() $\widetilde{g}|_{\partial_\infty Y_1}=g|_{\partial_\infty Y_1}$, then the answer to Question 4.5 is positive.
$\widetilde{g}|_{\partial_\infty Y_1}=g|_{\partial_\infty Y_1}$, then the answer to Question 4.5 is positive.
Finally, we remark that Theorem 1.1 is useful in understanding the arguments in [Reference Lukyanenko13, Reference Shanmugalingam and Xie16] concerning the bilipschitz extension of mappings from Gromov boundaries to the interiors of certain Gromov hyperbolic spaces. Indeed, we may obtain [Reference Shanmugalingam and Xie16, Corollaries 1.2 and 1.4] by combining [Reference Shanmugalingam and Xie16, Theorem 1.1] and the earlier mentioned results, particularly Corollary 4.3. Note that [Reference Lukyanenko13, Lemma 3.23] is a quantitative consequence of Theorem 1.1.
Funding Statement
Qingshan Zhou was partly supported by NNSF of China (No. 11901090), by Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515012441), by Department of Education of Guangdong Province, China (No. 2021KTSCX116). Qianghua Luo was supported by Guangdong Basic and Applied Basic Research Foundation (No. 2023A1515110902).