Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:44:53.431Z Has data issue: false hasContentIssue false
  • English
  • Français

Sufficient conditions for matchings

Published online by Cambridge University Press:  20 January 2009

Ian Anderson
Ian Anderson
Affiliation:
The Department of Mathematics, University Gardens, Glasgow G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A graph G is said to possess a perfect matching if there is a subgraph of G consisting of disjoint edges which together cover all the vertices of G. Clearly G must then have an even number of vertices. A necessary and sufficient condition for G to possess a perfect matching was obtained by Tutte (3). If S is any set of vertices of G, let p(S) denote the number of components of the graph G – S with an odd number of vertices. Then the condition

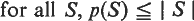
is both necessary and sufficient for the existence of a perfect matching. A simple proof of this result is given in (1).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 2 , December 1972 , pp. 129 - 136
Copyright
Copyright © Edinburgh Mathematical Society 1972

References

REFERENCES

(1) Anderson, I., Perfect matchings of a graph, J. Combinatorial Theory 10 (1971), 183–186.CrossRefGoogle Scholar
(2) Berge, C., The theory of graphs and its applications (Methuen, London, 1962).Google Scholar
(3) Tutte, W. T., The factorisation of linear graphs, J. London Math. Soc. 27 (1947), 107–111.CrossRefGoogle Scholar
(4) Woodall, D. R., The melting point of a graph, and its Anderson number (to appear).Google Scholar