Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T19:08:17.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong morita equivalence for conditional expectations

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  08 February 2022

Kazunori Kodaka Open the ORCID record for Kazunori Kodaka [Opens in a new window]
Kazunori Kodaka*
Affiliation:
Department of Mathematical Sciences, Faculty of Science, Ryukyu University, Nishihara-cho, Okinawa903-0213, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider two inclusions of $C^{*}$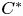-algebras whose small $C^{*}$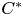-algebras have approximate units of the large $C^{*}$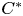-algebras and their two spaces of all bounded bimodule linear maps. We suppose that the two inclusions of $C^{*}$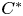-algebras are strongly Morita equivalent. In this paper, we shall show that there exists an isometric isomorphism from one of the spaces of all bounded bimodule linear maps to the other space and we shall study the basic properties about the isometric isomorphism. And, using this isometric isomorphism, we define the Picard group for a bimodule linear map and discuss the Picard group for a bimodule linear map.

Keywords

bimodule mapsinclusions of C*-algebrasconditional expectationsstrong Morita equivalence

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 182 - 213
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, L. G., Stable isomorphism of hereditary subalgebra of $C^{*}$-algebras, Pacific J. Math. 71 (1977), 335–348.CrossRefGoogle Scholar
Brown, L. G., Green, P. and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of $C^{*}$-algebras, Pacific J. Math. 71 (1977), 349–363.CrossRefGoogle Scholar
Frank, M. and Kirchberg, E., On conditional expectations of finite index, J. Oper. Theory 40 (1998), 87–111.Google Scholar
Izumi, M., Inclusions of simple $C^{*}$-algebras, J. Reine Angew. Math. 547 (2002), 97–138.Google Scholar
Jensen, K. K. and Thomsen, K., Elements of KK-theory (Birkhäuser, 1991).CrossRefGoogle Scholar
Kodaka, K., The Picard groups for unital inclusions of unital $C^{*}$-algebras, Acta Sci. Math. (Szeged) 86 (2020), 183–207.CrossRefGoogle Scholar
Kodaka, K., Strong Morita equivalence for inclusions of $C^{*}$-algebras induced by twisted actions of a countable discrete group, Math. Scand. 127 (2021), 317–336.CrossRefGoogle Scholar
Kodaka, K. and Teruya, T., The strong Morita equivalence for inclusions of $C^{*}$-algebras and conditional expectations for equivalence bimodules, J. Aust. Math. Soc. 105 (2018), 103–144.CrossRefGoogle Scholar
Pedersen, G. K., C*-algebras and their automorphism groups (London, New York, San Francisco, Academic Press, 1979).Google Scholar
Raeburn, I. and Williams, D. P., Morita equivalence and continuous-trace $C^{*}$-algebras, Mathematical Surveys and Monographs, Volume 60 (Amer. Math. Soc., 1998).CrossRefGoogle Scholar
Rieffel, M. A., $C^{*}$-algebras associated with irrational rotations, Pacific J. Math. 93 (1981), 415–429.CrossRefGoogle Scholar
Størmer, E., Positive linear maps of operator algebras, (Berlin, Heidelberg, Springer-Verlag, 2013).CrossRefGoogle Scholar
Watatani, Y., Index for $C^{*}$-subalgebras, Mem. Amer. Math. Soc., Volume 424 (Amer. Math. Soc., 1990).Google Scholar