Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T16:12:27.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral approximants of normal operators

Published online by Cambridge University Press:  20 January 2009

P. R. Halmos
P. R. Halmos
Affiliation:
Indiana University and University of Edinburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

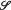For each non-empty subset Λ of the complex plane, let (Λ) be the set of all those operators (on a fixed Hilbert space H) whose spectrum is included in Λ. The problem of spectral approximation is to determine how closely each operator on H can be approximated (in the norm) by operators in 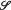(Λ). The problem appears to be connected with the stability theory of certain differential equations. (Consider the case in which Λ is the right half plane.) In its general form the problem is extraordinarily difficult. Thus, for instance, even when Λ is the singleton {0}, so that 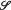(Λ) is the set of quasinilpotent operators, the determination of the closure of 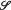(Λ) has been an open problem for several years (3, Problem 7).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 1 , March 1974 , pp. 51 - 58
Copyright
Copyright © Edinburgh Mathematical Society 1974

References

REFERENCES

(1) Fan, K. and Hoffman, A. J., Some metric inequalities in the space of matrices, Proc. Amer. Math. Soc. 6 (1955), 111–116.CrossRefGoogle Scholar
(2) Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, 1967).Google Scholar
(3) Halmos, P. R., Ten problems in Hilbert space, Bull. Amer. Math. Soc. 76 (1970), 887–933.CrossRefGoogle Scholar
(4) Halmos, P. R., Positive approximants of operators, Indiana Univ. Math. J. 21 (1972), 951–960.CrossRefGoogle Scholar
(5) Kuratowski, K. and Nardzewski, C. Ryll-, A general theorem on selectors, Bull. Acad. Polon. Sci. 13 (1965), 397–403.Google Scholar
(6) Newburgh, J. D., The variation of spectra, Duke Math. J. 18 (1951), 165–176.CrossRefGoogle Scholar
(7) Van Riemsduk, D. J., Some metric inequalities in the space of bounded linear operators on a separable Hilbert space, Nieuw Arch. Wisk. (3) 20 (1972), 216–230.Google Scholar
(8) Valentine, F. A., Convex sets (McGraw-Hill, New York, 1964).Google Scholar