Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:05:46.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Some theorems on absolute Cesàro summability

Published online by Cambridge University Press:  20 January 2009

J. M. Hyslop
J. M. Hyslop
Affiliation:
The University, Glasgow.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. It is convenient to begin with a brief statement of the notation which will be used throughout this paper.

Let k be any positive number and let

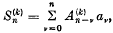
where 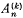is the coefficient of xn in the formal expansion of (1 – x )–k–1, and let

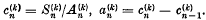
Then the series Σαn is said to be summable(C, k) if 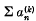is convergent, that is, if 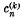tends to a limit, and absolutely summable (C, k), or summable |C, k|, if 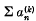is absolutely convergent.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 6 , Issue 2 , October 1939 , pp. 114 - 122
Copyright
Copyright © Edinburgh Mathematical Society 1939

References

page 114 note 1 Hyslop, J. M., Proc. Edinburgh Math. Soc. (2), 5 (1938), 182–201.CrossRefGoogle Scholar

page 115 note 1 Andersen, A. F., Proc. London Math. Soc. (2), 27 (1928), 39–71.CrossRefGoogle Scholar

page 115 note 2 Kogbefclianbz, E., Bull. des Sciences Math. (2), 49 (1925), 234–256.Google Scholar

page 115 note 3 See Andersen, A. F., Studier over Cesaro's Summabilitetsmetode (Copenhagen, 1921), 42,Google Scholar and Hyslop, J. M., loc. cit., 187.Google Scholar

page 116 note 1 Here as elsewhere A is independent of the variables under consideration and hasnot necessarily the same value each time it occurs.

page 122 note 1 Hyslop, J. M., Proc. Edinburgh Math. Soc. (2), 6 (1939), 51–56.CrossRefGoogle Scholar