Published online by Cambridge University Press: 27 December 2021
Let $\mathcal {O}(\pi )$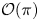 denote the number of odd parts in an integer partition $\pi$
denote the number of odd parts in an integer partition $\pi$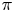 . In 2005, Stanley introduced a new statistic $\operatorname {srank}(\pi )=\mathcal {O}(\pi )-\mathcal {O}(\pi ')$
. In 2005, Stanley introduced a new statistic $\operatorname {srank}(\pi )=\mathcal {O}(\pi )-\mathcal {O}(\pi ')$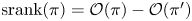 , where $\pi '$
, where $\pi '$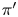 is the conjugate of $\pi$
is the conjugate of $\pi$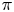 . Let $p(r,\,m;n)$
. Let $p(r,\,m;n)$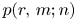 denote the number of partitions of $n$
denote the number of partitions of $n$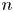 with srank congruent to $r$
with srank congruent to $r$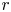 modulo $m$
modulo $m$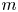 . Generating function identities, congruences and inequalities for $p(0,\,4;n)$
. Generating function identities, congruences and inequalities for $p(0,\,4;n)$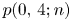 and $p(2,\,4;n)$
and $p(2,\,4;n)$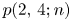 were then established by a number of mathematicians, including Stanley, Andrews, Swisher, Berkovich and Garvan. Motivated by these works, we deduce some generating functions and inequalities for $p(r,\,m;n)$
were then established by a number of mathematicians, including Stanley, Andrews, Swisher, Berkovich and Garvan. Motivated by these works, we deduce some generating functions and inequalities for $p(r,\,m;n)$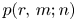 with $m=16$
with $m=16$ and $24$
and $24$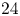 . These results are refinements of some inequalities due to Swisher.
. These results are refinements of some inequalities due to Swisher.