Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jones, P. R.
1980.
Congruences contained in an equivalence on a semigroup.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 29,
Issue. 2,
p.
162.
Mitsch, Heinz
1983.
Semigroups and their lattice of congruences.
Semigroup Forum,
Vol. 26,
Issue. 1,
p.
1.
Bonzini, C.
and
Cherubini, A.
1990.
Semimodularity of the congruence lattice on regular ?-semigroups.
Monatshefte f�r Mathematik,
Vol. 109,
Issue. 3,
p.
205.


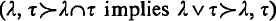 . This result may be stated: If
. This result may be stated: If 