Published online by Cambridge University Press: 28 May 2009
Semiclassical limits of generic multi-parameter quantized coordinate rings A=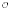 q(kn) of affine spaces are constructed and related to A, for k an algebraically closed field of characteristic zero and q a multiplicatively antisymmetric matrix whose entries generate a torsion-free subgroup of k×. A semiclassical limit of A is a Poisson algebra structure on the corresponding classical coordinate ring R=
q(kn) of affine spaces are constructed and related to A, for k an algebraically closed field of characteristic zero and q a multiplicatively antisymmetric matrix whose entries generate a torsion-free subgroup of k×. A semiclassical limit of A is a Poisson algebra structure on the corresponding classical coordinate ring R=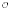 (kn), and results of Oh, Park, Shin and the authors are used to construct homeomorphisms from the Poisson-prime and Poisson-primitive spectra of R onto the prime and primitive spectra of~A. The Poisson-primitive spectrum of R is then identified with the space of symplectic cores in kn in the sense of Brown and Gordon, and an example is presented (over ℂ) for which the Poisson-primitive spectrum of R is not homeomorphic to the space of symplectic leaves in kn. Finally, these results are extended from quantum affine spaces to quantum affine toric varieties.
(kn), and results of Oh, Park, Shin and the authors are used to construct homeomorphisms from the Poisson-prime and Poisson-primitive spectra of R onto the prime and primitive spectra of~A. The Poisson-primitive spectrum of R is then identified with the space of symplectic cores in kn in the sense of Brown and Gordon, and an example is presented (over ℂ) for which the Poisson-primitive spectrum of R is not homeomorphic to the space of symplectic leaves in kn. Finally, these results are extended from quantum affine spaces to quantum affine toric varieties.