Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alonso, J.M
1996.
Dehn functions and finiteness properties of graph products.
Journal of Pure and Applied Algebra,
Vol. 107,
Issue. 1,
p.
9.
Polyakova, L. Yu.
2007.
Resolutions for free partially commutative monoids.
Siberian Mathematical Journal,
Vol. 48,
Issue. 6,
p.
1038.
Genevois, Anthony
2023.
Special cube complexes revisited: a quasi-median generalization.
Canadian Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
743.


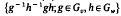 for all adjacent
for all adjacent 