Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T21:29:10.518Z Has data issue: false hasContentIssue false
  • English
  • Français

A procedure for summing asymptotic series

Published online by Cambridge University Press:  20 January 2009

R. E. Scraton
R. E. Scraton
Affiliation:
University of Bradford, Bradford 7 Yorks
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

When a function ƒ(x) possesses an asymptotic series

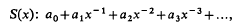
this series provides a useful means of evaluating ƒ(x) for large values of x. The usual procedure is to sum all the terms in S(x) up to, but excluding, the term of smallest magnitude. The degree of accuracy obtained by this method cannot normally be improved by direct summation of S(x), but sometimes better accuracy can be obtained by using one of the familiar devices for accelerating the convergence of series. Simple δ2-extrapolation may be successful, and Rosser (1) and others have used the Euler transformation to some effect. The method given here provides, in suitable cases, a more effective means of evaluating ƒ(x) from the series for a wide range of values of x.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 317 - 324
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERECNCES

(1) Rosser, J. B.Transformations to speed the convergence of series J. Res. Nat. Bur. Stand. 46 (1951), 56.CrossRefGoogle Scholar
(2) Scraton, R. E.A note on the summation of divergent power series, Proc. Cambridge Philos. Soc. 66 (1969), 109.CrossRefGoogle Scholar
(3) Ser, J.Sur la valeur numérique des intégrales employées dans la sommation exponentielle, Bull. Sci. Math. (2) 60 (1936), 199.Google Scholar
(4) Ser, J.Quelques applications des polynomes de Laguerre, Bull. Sci. Math. (2) 61 (1937), 74.Google Scholar
(5) Ser, J.Formules et tables pour le calcul numérique de certaines series divergentes. Bull. Math. Sci., (2) 62 (1938), 171.Google Scholar
(6) Wijngaarden, A. Van, A transformation of formal series, Proc. Kon. Ned. Ak. v. Wet., Ser. A, 56 (1953), 522.Google Scholar