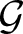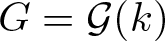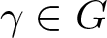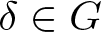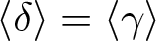1. The main result
Let G be a group. We say that G has the Honda property Footnote 1 if for any ![]() $\gamma\in G$ such that γ is a commutator and for any
$\gamma\in G$ such that γ is a commutator and for any ![]() $\delta\in G$ such that
$\delta\in G$ such that ![]() $\langle \delta\rangle= \langle \gamma\rangle$, δ is also a commutator. If γ has infinite order then the only generators of
$\langle \delta\rangle= \langle \gamma\rangle$, δ is also a commutator. If γ has infinite order then the only generators of ![]() $\langle \gamma\rangle$ are
$\langle \gamma\rangle$ are ![]() $\delta= \gamma^{\pm 1}$, so the condition above is only of interest when γ has finite order. The following result was proved by Honda in 1953 [Reference Honda8].
$\delta= \gamma^{\pm 1}$, so the condition above is only of interest when γ has finite order. The following result was proved by Honda in 1953 [Reference Honda8].
Theorem 1.1.
Any finite group has the Honda property.
Honda’s original proof is character-theoretic. Recently, Lenstra has given a short and elegant proof that avoids character theory completely [Reference Lenstra9].
It is natural to ask which other groups have the Honda property. Pride has given an example of a one-relator group with torsion which does not have the Honda property [Reference Pride16, Result (C), p. 488]. In this note, we extend Theorem 1.1 to certain linear algebraic groups. By a linear algebraic group over a ring k, we mean a smooth closed subgroup scheme of GLn for some ![]() $n\in {\mathbb N}$; if k is a field then these are just linear algebraic groups in the usual sense [Reference Borel1], and they correspond to the affine algebraic groups of finite type by [Reference Milne14, Corollary 4.10].
$n\in {\mathbb N}$; if k is a field then these are just linear algebraic groups in the usual sense [Reference Borel1], and they correspond to the affine algebraic groups of finite type by [Reference Milne14, Corollary 4.10].
Theorem 1.2.
Let ![]() ${\mathcal G}$ be a linear algebraic group over k and let
${\mathcal G}$ be a linear algebraic group over k and let ![]() $G= {\mathcal G}(k)$, where k is one of the following.
$G= {\mathcal G}(k)$, where k is one of the following.
(a) An algebraically closed field.
(b) A pseudo-finite field.
(c) The valuation ring of a non-archimedean local field.
Then G has the Honda property.
Remark 1.3. Let us say a group G has the strong Honda property if for any ![]() $\alpha, \beta\in G$ and any
$\alpha, \beta\in G$ and any ![]() $\delta\in G$ such that
$\delta\in G$ such that ![]() $\langle \delta\rangle= \langle [\alpha, \beta]\rangle$, there exist
$\langle \delta\rangle= \langle [\alpha, \beta]\rangle$, there exist ![]() $\sigma, \tau\in \langle \alpha, \beta\rangle$ such that
$\sigma, \tau\in \langle \alpha, \beta\rangle$ such that ![]() $\delta= [\sigma, \tau]$. Clearly, if G has the strong Honda property then G has the Honda property and any subgroup of G has the strong Honda property. Theorem 1.1 implies that any locally finite group has the strong Honda property. In particular, if
$\delta= [\sigma, \tau]$. Clearly, if G has the strong Honda property then G has the Honda property and any subgroup of G has the strong Honda property. Theorem 1.1 implies that any locally finite group has the strong Honda property. In particular, if ![]() ${\mathcal G}$ is a linear algebraic group over
${\mathcal G}$ is a linear algebraic group over ![]() $\overline{{\mathbb F}_p}$ then
$\overline{{\mathbb F}_p}$ then ![]() ${\mathcal G}(\overline{{\mathbb F}_p})$ is locally finite, so
${\mathcal G}(\overline{{\mathbb F}_p})$ is locally finite, so ![]() ${\mathcal G}(\overline{{\mathbb F}_p})$ has the strong Honda property. (Here
${\mathcal G}(\overline{{\mathbb F}_p})$ has the strong Honda property. (Here ![]() $\overline{{\mathbb F}_p}$ denotes the algebraic closure of the field with p elements.)
$\overline{{\mathbb F}_p}$ denotes the algebraic closure of the field with p elements.)
On the other hand, none of ![]() ${\rm (P)GL}_n({\mathbb C})$,
${\rm (P)GL}_n({\mathbb C})$, ![]() ${\rm (P)GL}_n({\mathbb R})$,
${\rm (P)GL}_n({\mathbb R})$, ![]() ${\rm (P)SL}_n({\mathbb C})$ and
${\rm (P)SL}_n({\mathbb C})$ and ![]() ${\rm (P)SL}_n({\mathbb R})$ has the strong Honda property if
${\rm (P)SL}_n({\mathbb R})$ has the strong Honda property if ![]() $n\geq 2$, so Theorem 1.2(a) fails if we replace the Honda property with the strong Honda property. To see this, consider the group
$n\geq 2$, so Theorem 1.2(a) fails if we replace the Honda property with the strong Honda property. To see this, consider the group ![]() $\Gamma_s= \langle a,b\,|\,[a,b]^s\rangle$. Pride (loc. cit.) shows that if
$\Gamma_s= \langle a,b\,|\,[a,b]^s\rangle$. Pride (loc. cit.) shows that if ![]() $0 \lt t \lt s$ then
$0 \lt t \lt s$ then ![]() $[a,b]^t$ is not a commutator in
$[a,b]^t$ is not a commutator in ![]() $\Gamma_s$ unless
$\Gamma_s$ unless ![]() $t\equiv \pm 1\! \mod\! s$, so
$t\equiv \pm 1\! \mod\! s$, so ![]() $\Gamma_s$ does not have the Honda property if s > 6 (choose
$\Gamma_s$ does not have the Honda property if s > 6 (choose ![]() $2\leq t\leq s- 2$ such that t is coprime to s). The group
$2\leq t\leq s- 2$ such that t is coprime to s). The group ![]() $\Gamma_s$ is Fuchsian (cf. [Reference Long, Maclachlan and Reid10, § 1]), so it is a subgroup of
$\Gamma_s$ is Fuchsian (cf. [Reference Long, Maclachlan and Reid10, § 1]), so it is a subgroup of ![]() ${\rm PSL}_2({\mathbb R})$. Hence
${\rm PSL}_2({\mathbb R})$. Hence ![]() ${\rm PSL}_2({\mathbb R})$ does not have the strong Honda property, so
${\rm PSL}_2({\mathbb R})$ does not have the strong Honda property, so ![]() ${\rm PSL}_2({\mathbb C})$,
${\rm PSL}_2({\mathbb C})$, ![]() ${\rm PGL}_2({\mathbb R})$ and
${\rm PGL}_2({\mathbb R})$ and ![]() ${\rm PGL}_2({\mathbb C})$ also do not have the strong Honda property. Now choose lifts
${\rm PGL}_2({\mathbb C})$ also do not have the strong Honda property. Now choose lifts ![]() $\widehat{a}$ (resp.,
$\widehat{a}$ (resp., ![]() $\widehat{b}$) of a (resp., b) to elements of
$\widehat{b}$) of a (resp., b) to elements of ![]() ${\rm SL}_2({\mathbb R})$, and let
${\rm SL}_2({\mathbb R})$, and let  $\widehat{\Gamma}_s= \langle \widehat{a}, \widehat{b}\rangle$. The element
$\widehat{\Gamma}_s= \langle \widehat{a}, \widehat{b}\rangle$. The element  $[\widehat{a}, \widehat{b}]$ has order either s or 2s, and
$[\widehat{a}, \widehat{b}]$ has order either s or 2s, and  $[\widehat{a}, \widehat{b}]^t$ is not a commutator in
$[\widehat{a}, \widehat{b}]^t$ is not a commutator in ![]() $\widehat{\Gamma}_s$ if
$\widehat{\Gamma}_s$ if ![]() $0 \lt t \lt s$ and
$0 \lt t \lt s$ and ![]() $t\not\equiv \pm 1\mod s$. Hence
$t\not\equiv \pm 1\mod s$. Hence ![]() ${\rm SL}_2({\mathbb R})$ does not have the strong Honda property (choose s > 6 and choose
${\rm SL}_2({\mathbb R})$ does not have the strong Honda property (choose s > 6 and choose ![]() $2\leq t\leq s- 2$ such that t is coprime to 2s), so
$2\leq t\leq s- 2$ such that t is coprime to 2s), so ![]() ${\rm GL}_2({\mathbb R})$,
${\rm GL}_2({\mathbb R})$, ![]() ${\rm SL}_2({\mathbb C})$ and
${\rm SL}_2({\mathbb C})$ and ![]() ${\rm GL}_2({\mathbb C})$ also do not have the strong Honda property. Since we may embed
${\rm GL}_2({\mathbb C})$ also do not have the strong Honda property. Since we may embed ![]() ${\rm SL}_2({\mathbb R})$ as a subgroup of
${\rm SL}_2({\mathbb R})$ as a subgroup of ![]() ${\rm (P)GL}_n({\mathbb C})$,
${\rm (P)GL}_n({\mathbb C})$, ![]() ${\rm (P)GL}_n({\mathbb R})$,
${\rm (P)GL}_n({\mathbb R})$, ![]() ${\rm (P)SL}_n({\mathbb C})$ and
${\rm (P)SL}_n({\mathbb C})$ and ![]() ${\rm (P)SL}_n({\mathbb R})$ for any
${\rm (P)SL}_n({\mathbb R})$ for any ![]() $n\geq 3$, the assertion above follows.
$n\geq 3$, the assertion above follows.
The proof of Theorem 1.2(a) uses the Lefschetz principle from first-order model theory. The idea is very simple. Let ![]() ${\mathcal G}$ be a linear algebraic group over an algebraically closed field k. For the moment, assume
${\mathcal G}$ be a linear algebraic group over an algebraically closed field k. For the moment, assume ![]() ${\mathcal G}$ is defined over the prime field F. Set
${\mathcal G}$ is defined over the prime field F. Set ![]() $G= {\mathcal G}(k)$. We can find an F-embedding of
$G= {\mathcal G}(k)$. We can find an F-embedding of ![]() ${\mathcal G}$ as a closed subgroup of SLn for some n: so G is defined as a subset of
${\mathcal G}$ as a closed subgroup of SLn for some n: so G is defined as a subset of ![]() ${\rm SL}_n(k)$ by polynomials over F in n 2 variables and the group operations on G are given by polynomial maps over F. If
${\rm SL}_n(k)$ by polynomials over F in n 2 variables and the group operations on G are given by polynomial maps over F. If ![]() $\gamma, \delta\in G$ then
$\gamma, \delta\in G$ then ![]() $\langle \delta\rangle= \langle \gamma\rangle$ if and only if
$\langle \delta\rangle= \langle \gamma\rangle$ if and only if ![]() $\delta= \gamma^s$ and
$\delta= \gamma^s$ and ![]() $\gamma= \delta^t$ for some
$\gamma= \delta^t$ for some ![]() $s,t\in {\mathbb Z}$. For fixed s and t, we observe that the condition
$s,t\in {\mathbb Z}$. For fixed s and t, we observe that the condition
is given by a first-order sentence in the language of rings involving the n 2 variables of the ambient affine space. Now ![]() $(*)_{s,t}$ is true if
$(*)_{s,t}$ is true if ![]() $k= \overline{{\mathbb F}_p}$ for any prime p, by Remark 1.3. It follows from the Lefschetz principle that
$k= \overline{{\mathbb F}_p}$ for any prime p, by Remark 1.3. It follows from the Lefschetz principle that ![]() $(*)_{s,t}$ is true for every algebraically closed field k, including the characteristic 0 case. But s and t were arbitrary integers, so the result follows. On the other hand, we see from Remark 1.3 that the analogous argument fails for the strong Honda property, so the strong Honda property cannot be expressed in a first-order way.
$(*)_{s,t}$ is true for every algebraically closed field k, including the characteristic 0 case. But s and t were arbitrary integers, so the result follows. On the other hand, we see from Remark 1.3 that the analogous argument fails for the strong Honda property, so the strong Honda property cannot be expressed in a first-order way.
If G is not defined over the prime field F then the argument above needs modification. The trouble is that the polynomials that define G as a closed subgroup of ![]() ${\rm SL}_n(k)$ may involve parameters from k, so
${\rm SL}_n(k)$ may involve parameters from k, so ![]() $(*)_{s,t}$ may fail to translate into an honest sentence. We get around this by using a trick from [Reference Martin, Stewart and Topley13] (cf. also the discussion after Theorem 1.1 of [Reference Martin, Stewart and Topley12]): first, we replace these parameters with variables, then we quantify over all possible values of these variables. This amounts to quantifying over all linear algebraic groups of bounded complexity in an appropriate sense. In [Reference Martin, Stewart and Topley13, § 3.2], this idea is formulated using the language of Hopf algebras; here we give a more concrete description.
$(*)_{s,t}$ may fail to translate into an honest sentence. We get around this by using a trick from [Reference Martin, Stewart and Topley13] (cf. also the discussion after Theorem 1.1 of [Reference Martin, Stewart and Topley12]): first, we replace these parameters with variables, then we quantify over all possible values of these variables. This amounts to quantifying over all linear algebraic groups of bounded complexity in an appropriate sense. In [Reference Martin, Stewart and Topley13, § 3.2], this idea is formulated using the language of Hopf algebras; here we give a more concrete description.
We present the details in § 2. The proof of Theorem 1.2(b) follows from a closely related argument. We prove Theorem 1.2(c) in § 3.
Remark 1.4. J. Wilson gives some other first-order properties of groups that hold for finite groups but not for arbitrary groups [Reference Wilson19]; see [Reference Wilson18], [Reference Cornulier and Wilson5]. One can use the methods of this paper to prove that these properties hold for linear algebraic groups over an algebraically closed or pseudo-finite field. Likewise, Theorem 1.2 holds for definable groups in the sense of [Reference Peterzil, Pillay and Starchenko15, Introduction] over an algebraically closed or pseudo-finite field k; in particular, this includes group schemes of finite type over such k. I’m grateful to Lenstra and Tiersma for these observations.
2. Model theory and the Lefschetz principle
We give a brief review of the model theory we need to prove Theorem 1.2. For more details, see [Reference Marker11]. We work in the language of rings, which consists of two binary function symbols + and · and two constant symbols 0 and 1. A formula is a well-formed expression involving +, ·, =, 0 and 1, the symbols ![]() $\vee$ (or),
$\vee$ (or), ![]() $\wedge$ (and),
$\wedge$ (and), ![]() $\rightarrow$ (implies),
$\rightarrow$ (implies), ![]() $\neg$ (not), some variables and the quantifiers
$\neg$ (not), some variables and the quantifiers ![]() $\forall$ and
$\forall$ and ![]() $\exists$. For instance,
$\exists$. For instance, ![]() $(\exists Y)\,Y^2= X$ and
$(\exists Y)\,Y^2= X$ and ![]() $(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$ and
$(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$ and ![]() $X\neq 0 \rightarrow X^2= X$ are formulas. The variable X in the first formula is free because it is not attached to a quantifier, while the variable Y is bound. A sentence is a formula with no free variables; the second formula above is a sentence. For any given ring k, a sentence is either true or false: for instance, the sentence
$X\neq 0 \rightarrow X^2= X$ are formulas. The variable X in the first formula is free because it is not attached to a quantifier, while the variable Y is bound. A sentence is a formula with no free variables; the second formula above is a sentence. For any given ring k, a sentence is either true or false: for instance, the sentence ![]() $(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$ is true when
$(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$ is true when ![]() $k= {\mathbb C}$ and false when
$k= {\mathbb C}$ and false when ![]() $k= {\mathbb R}$. If a formula involves one or more free variables then it doesn’t make sense to ask whether it is true or false for a particular ring k; but if
$k= {\mathbb R}$. If a formula involves one or more free variables then it doesn’t make sense to ask whether it is true or false for a particular ring k; but if ![]() $\psi(X_1,\ldots, X_m)$ is a formula in free variables
$\psi(X_1,\ldots, X_m)$ is a formula in free variables ![]() $X_1, \ldots, X_m$, k is a ring and
$X_1, \ldots, X_m$, k is a ring and ![]() $\alpha_1,\ldots, \alpha_m\in k$ then the expression
$\alpha_1,\ldots, \alpha_m\in k$ then the expression ![]() $\psi(\alpha_1,\ldots, \alpha_m)$ we get by substituting
$\psi(\alpha_1,\ldots, \alpha_m)$ we get by substituting ![]() $X_i= \alpha_i$ for
$X_i= \alpha_i$ for ![]() $1\leq i\leq m$ is either true or false.
$1\leq i\leq m$ is either true or false.
We can turn a formula into a sentence by quantifying over the free variables: e.g. quantifying over all X in the third formula above gives the sentence ![]() $(\forall X)\,X\neq 0 \rightarrow X^2= X$, which is false for any field with more than two elements. Note that if
$(\forall X)\,X\neq 0 \rightarrow X^2= X$, which is false for any field with more than two elements. Note that if ![]() $k= {\mathbb R}$ then the expression
$k= {\mathbb R}$ then the expression ![]() $(\forall X)(\exists Y)\, Y^2= \pi X$ is not a sentence in the above sense as it involves the real parameter π. This problem does not arise with the expression
$(\forall X)(\exists Y)\, Y^2= \pi X$ is not a sentence in the above sense as it involves the real parameter π. This problem does not arise with the expression ![]() $(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$: we don’t need to regard 2 as a real parameter, because we get
$(\forall X) (\exists Y) (\exists Z)\,X= Y^2+ Z^2+ 2$: we don’t need to regard 2 as a real parameter, because we get ![]() $2= 1+1$ for free by adding the constant symbol 1 to itself. More generally, if
$2= 1+1$ for free by adding the constant symbol 1 to itself. More generally, if ![]() $f(X_1,\ldots, X_m)$ is a polynomial over
$f(X_1,\ldots, X_m)$ is a polynomial over ![]() ${\mathbb Z}$ in variables
${\mathbb Z}$ in variables ![]() $X_1,\ldots, X_m$ then (say) the expression
$X_1,\ldots, X_m$ then (say) the expression ![]() $(\exists X_1)\cdots (\exists X_m)\, f(X_1,\ldots, X_m)= 0$ is a sentence.
$(\exists X_1)\cdots (\exists X_m)\, f(X_1,\ldots, X_m)= 0$ is a sentence.
An infinite field k is pseudo-finite if it is a model of the theory of finite fields: that is, a sentence is true for k if it is true for every finite field. A non-principal ultraproduct of an infinite collection of finite fields is pseudo-finite. For instance, if ![]() ${\mathcal U}$ is a non-principal ultrafilter on the set of all primes then the ultraproduct
${\mathcal U}$ is a non-principal ultrafilter on the set of all primes then the ultraproduct ![]() $\prod_{\mathcal U} {\mathbb F}_p$ is a pseudo-finite field of characteristic 0, and many of the infinite subfields of
$\prod_{\mathcal U} {\mathbb F}_p$ is a pseudo-finite field of characteristic 0, and many of the infinite subfields of ![]() $\overline{{\mathbb F}_p}$ are pseudo-finite fields of characteristic p. See [Reference Chatzidakis2] and [Reference Chatzidakis3, (5.1)] for more details and examples.
$\overline{{\mathbb F}_p}$ are pseudo-finite fields of characteristic p. See [Reference Chatzidakis2] and [Reference Chatzidakis3, (5.1)] for more details and examples.
We will use the following version of the Lefschetz principle (see [Reference Marker11, Corollary 2.2.9 and Corollary 2.2.10]).
Theorem 2.1 (The Lefschetz principle)
Let ψ be a sentence.
(a) Let p be 0 or a prime. If ψ is true for some algebraically closed field of characteristic p then ψ is true for every algebraically closed field of characteristic p.
(b) ψ is true for some algebraically closed field of characteristic 0 if and only if for all but finitely many primes p, ψ is true for some algebraically closed field of characteristic p.
We have an immediate corollary.
Corollary 2.2. Let ψ be a sentence. If ψ is true for ![]() $k= \overline{{\mathbb F}_p}$ for every prime p then ψ is true for every algebraically closed field.
$k= \overline{{\mathbb F}_p}$ for every prime p then ψ is true for every algebraically closed field.
Now fix a field k. Let ![]() ${\mathcal G}$ be a linear algebraic group over k. Choose an embedding of
${\mathcal G}$ be a linear algebraic group over k. Choose an embedding of ![]() ${\mathcal G}$ as a closed subgroup of SLn for some n. We regard
${\mathcal G}$ as a closed subgroup of SLn for some n. We regard ![]() ${\rm SL}_n(k)$ as a subset of affine space
${\rm SL}_n(k)$ as a subset of affine space ![]() $k^{n^2}$ in the usual way. Denote the co-ordinates of
$k^{n^2}$ in the usual way. Denote the co-ordinates of ![]() $k^{n^2}$ by Xij for
$k^{n^2}$ by Xij for ![]() $1\leq i\leq n$ and
$1\leq i\leq n$ and ![]() $1\leq j\leq n$. Let
$1\leq j\leq n$. Let ![]() $G= {\mathcal G}(k)$. Our embedding of
$G= {\mathcal G}(k)$. Our embedding of ![]() ${\mathcal G}$ in SLn allows us to regard G as a subset of
${\mathcal G}$ in SLn allows us to regard G as a subset of ![]() $k^{n^2}$ given by the set of zeroes of some polynomials
$k^{n^2}$ given by the set of zeroes of some polynomials ![]() $f_1(X_{ij}),\ldots, f_r(X_{ij})$ over k in the Xij.
$f_1(X_{ij}),\ldots, f_r(X_{ij})$ over k in the Xij.
Fix ![]() $s,t\in {\mathbb Z}$. We want to interpret the condition in
$s,t\in {\mathbb Z}$. We want to interpret the condition in ![]() $(*)_{s,t}$ as a sentence. The subset
$(*)_{s,t}$ as a sentence. The subset ![]() ${\rm SL}_n(k)$ of
${\rm SL}_n(k)$ of ![]() $k^{n^2}$ is the set of zeroes of finitely many polynomials over
$k^{n^2}$ is the set of zeroes of finitely many polynomials over ![]() ${\mathbb Z}$ in the matrix entries and the group operations on
${\mathbb Z}$ in the matrix entries and the group operations on ![]() ${\rm SL}_n(k)$ are given by polynomials over
${\rm SL}_n(k)$ are given by polynomials over ![]() ${\mathbb Z}$ in the matrix entries, so the conditions on
${\mathbb Z}$ in the matrix entries, so the conditions on ![]() $\alpha, \beta, \gamma, \delta, \sigma, \tau\in {\rm SL}_n(k)$ that
$\alpha, \beta, \gamma, \delta, \sigma, \tau\in {\rm SL}_n(k)$ that ![]() $\delta= \gamma^s$,
$\delta= \gamma^s$, ![]() $\gamma^t= \delta$,
$\gamma^t= \delta$, ![]() $\gamma= [\alpha, \beta]$ and
$\gamma= [\alpha, \beta]$ and ![]() $\delta= [\sigma, \tau]$ are given by formulas in the matrix entries of
$\delta= [\sigma, \tau]$ are given by formulas in the matrix entries of ![]() $\alpha, \beta, \gamma, \delta, \sigma$ and τ. (For instance, if we denote the co-ordinates of α by Xij then the condition
$\alpha, \beta, \gamma, \delta, \sigma$ and τ. (For instance, if we denote the co-ordinates of α by Xij then the condition ![]() $\alpha\in {\rm SL}_n(k)$ is given by the formula
$\alpha\in {\rm SL}_n(k)$ is given by the formula ![]() ${\rm det}(X_{ij})- 1= 0$.) However, the conditions
${\rm det}(X_{ij})- 1= 0$.) However, the conditions ![]() $\alpha, \beta, \gamma, \delta, \sigma, \tau\in G$ may fail to be given by formulas as the polynomials
$\alpha, \beta, \gamma, \delta, \sigma, \tau\in G$ may fail to be given by formulas as the polynomials ![]() $f_l(X_{ij})$ may involve some arbitrary elements of k.
$f_l(X_{ij})$ may involve some arbitrary elements of k.
We avoid this problem as follows. Fix ![]() $r\geq n$, let
$r\geq n$, let ![]() $m_1(X_{ij}),\ldots, m_c(X_{ij})$ be a listing (in some fixed but arbitrary order) of all the monomials in the Xij of total degree at most r, and let Vr be the subspace of the polynomial ring
$m_1(X_{ij}),\ldots, m_c(X_{ij})$ be a listing (in some fixed but arbitrary order) of all the monomials in the Xij of total degree at most r, and let Vr be the subspace of the polynomial ring ![]() $k[X_{ij}]$ spanned by the
$k[X_{ij}]$ spanned by the ![]() $m_e(X_{ij})$. Let Zab for
$m_e(X_{ij})$. Let Zab for ![]() $1\leq a\leq c$ and
$1\leq a\leq c$ and ![]() $1\leq b\leq c$ be variables. Define
$1\leq b\leq c$ be variables. Define ![]() $g_d(X_{ij}, Z_{ab})= \sum_{e= 1}^c Z_{ed}m_e(X_{ij})$ for
$g_d(X_{ij}, Z_{ab})= \sum_{e= 1}^c Z_{ed}m_e(X_{ij})$ for ![]() $1\leq d\leq c$. Now let
$1\leq d\leq c$. Now let ![]() $\epsilon= (\epsilon_{ab})_{1\leq a\leq c, 1\leq b\leq c}$ be a tuple of elements of k. We define
$\epsilon= (\epsilon_{ab})_{1\leq a\leq c, 1\leq b\leq c}$ be a tuple of elements of k. We define
 \begin{equation*}
G_\epsilon= \{\eta_{ij}\in k^{n^2}\,|\,{\rm det}(\eta_{ij})= 1\ \mbox{and}\ g_d(\eta_{ij}, \epsilon_{ab})= 0\ \mbox{for}\ 1\leq d\leq c\}.
\end{equation*}
\begin{equation*}
G_\epsilon= \{\eta_{ij}\in k^{n^2}\,|\,{\rm det}(\eta_{ij})= 1\ \mbox{and}\ g_d(\eta_{ij}, \epsilon_{ab})= 0\ \mbox{for}\ 1\leq d\leq c\}.
\end{equation*} If H is a subgroup of ![]() ${\rm SL}_n(k)$ defined by polynomials over k in the Xij of degree at most r then we say H has complexity at most r: in particular, Gϵ has complexity at most r.Footnote 2 Conversely, any closed subgroup H of complexity at most r is of the form Gϵ for some ϵ (note that we need at most c polynomials of the form gd to define a subgroup of complexity at most r because
${\rm SL}_n(k)$ defined by polynomials over k in the Xij of degree at most r then we say H has complexity at most r: in particular, Gϵ has complexity at most r.Footnote 2 Conversely, any closed subgroup H of complexity at most r is of the form Gϵ for some ϵ (note that we need at most c polynomials of the form gd to define a subgroup of complexity at most r because ![]() $\dim V_r= c$). Any closed subgroup of
$\dim V_r= c$). Any closed subgroup of ![]() ${\rm SL}_n(k)$ has complexity at most r′ for some
${\rm SL}_n(k)$ has complexity at most r′ for some ![]() $r^\prime\geq n$.
$r^\prime\geq n$.
Let ![]() $\phi(Z_{ab})$ be the formula in free variables Zab given by
$\phi(Z_{ab})$ be the formula in free variables Zab given by
 \begin{align*}
(\forall U_{ij})(\forall V_{ij}) [[{\rm det}(U_{ij})&= 1\wedge {\rm det}(V_{ij})= 1]\wedge [g_d(U_{ij}, Z_{ab})= 0 \wedge g_d(V_{ij}, Z_{ab})\\
&= 0\ \mbox{for}\ 1\leq d\leq c]]
\end{align*}
\begin{align*}
(\forall U_{ij})(\forall V_{ij}) [[{\rm det}(U_{ij})&= 1\wedge {\rm det}(V_{ij})= 1]\wedge [g_d(U_{ij}, Z_{ab})= 0 \wedge g_d(V_{ij}, Z_{ab})\\
&= 0\ \mbox{for}\ 1\leq d\leq c]]
\end{align*} where Wij is shorthand for ![]() $\sum_{l= 1}^n U_{il}V_{lj}$. Then Gϵ is closed under multiplication if and only if
$\sum_{l= 1}^n U_{il}V_{lj}$. Then Gϵ is closed under multiplication if and only if ![]() $\phi(\epsilon_{ab})$ is true. Likewise, there are formulas
$\phi(\epsilon_{ab})$ is true. Likewise, there are formulas ![]() $\chi(Z_{ab})$ and
$\chi(Z_{ab})$ and ![]() $\eta(Z_{ab})$ such that Gϵ is closed under taking inverses if and only if
$\eta(Z_{ab})$ such that Gϵ is closed under taking inverses if and only if ![]() $\chi(\epsilon_{ab})$ is true, and the identity I belongs to Gϵ if and only if
$\chi(\epsilon_{ab})$ is true, and the identity I belongs to Gϵ if and only if ![]() $\eta(\epsilon_{ab})$ is true.
$\eta(\epsilon_{ab})$ is true.
Now consider the condition ![]() $\psi_{n,s,t,r}$ given by
$\psi_{n,s,t,r}$ given by
 \begin{align*}
(\forall \alpha\in G_Z)(\forall \beta\in G_Z)(\forall \delta\in G_Z) (\delta= [\alpha, \beta]^s \wedge [\alpha, \beta]= \delta^t) \rightarrow ((\exists \sigma\in G_Z)(\exists \tau\in G_Z)\,\delta \\
= [\sigma, \tau]),
\end{align*}
\begin{align*}
(\forall \alpha\in G_Z)(\forall \beta\in G_Z)(\forall \delta\in G_Z) (\delta= [\alpha, \beta]^s \wedge [\alpha, \beta]= \delta^t) \rightarrow ((\exists \sigma\in G_Z)(\exists \tau\in G_Z)\,\delta \\
= [\sigma, \tau]),
\end{align*} where ![]() $\alpha= (\alpha_{ij}), \beta= (\beta_{ij}), \dots$ are tuples representing elements of
$\alpha= (\alpha_{ij}), \beta= (\beta_{ij}), \dots$ are tuples representing elements of ![]() ${\rm SL}_n(k)$. Here
${\rm SL}_n(k)$. Here ![]() $\alpha\in G_Z$ is shorthand for
$\alpha\in G_Z$ is shorthand for  $[{\rm det}(\alpha_{ij})= 1]\wedge \left[\bigwedge_{1\leq d\leq c} g_d(\alpha_{ij}, Z_{ab})= 0\right]$, and likewise for
$[{\rm det}(\alpha_{ij})= 1]\wedge \left[\bigwedge_{1\leq d\leq c} g_d(\alpha_{ij}, Z_{ab})= 0\right]$, and likewise for ![]() $\beta\in G_Z$, etc. We regard
$\beta\in G_Z$, etc. We regard ![]() $\psi_{n,s,t,r}$ as a sentence in variables Zab, αij, βij, etc. The above discussion yields the following: for any field k and for any
$\psi_{n,s,t,r}$ as a sentence in variables Zab, αij, βij, etc. The above discussion yields the following: for any field k and for any ![]() $n,s,t,r$, the sentence
$n,s,t,r$, the sentence ![]() $\psi_{n,s,t,r}$ is true for k if and only if
$\psi_{n,s,t,r}$ is true for k if and only if
![]() $(\dagger)$ for every closed subgroup G of
$(\dagger)$ for every closed subgroup G of ![]() ${\rm SL}_n(k)$ of complexity at most r and for every
${\rm SL}_n(k)$ of complexity at most r and for every ![]() $\alpha, \beta, \delta\in G$ such that
$\alpha, \beta, \delta\in G$ such that ![]() $\delta= [\alpha, \beta]^s$ and
$\delta= [\alpha, \beta]^s$ and ![]() $[\alpha, \beta]= \delta^t$, there exist
$[\alpha, \beta]= \delta^t$, there exist ![]() $\sigma, \tau\in G$ such that
$\sigma, \tau\in G$ such that ![]() $\delta= [\sigma, \tau]$.
$\delta= [\sigma, \tau]$.
We see from the above discussion that
Proposition 2.3. Let ![]() $n\in {\mathbb N}$, let
$n\in {\mathbb N}$, let ![]() $r\geq n$ and let
$r\geq n$ and let ![]() $s,t\in {\mathbb Z}$. Let k be an algebraically closed field or a pseudo-finite field. Then
$s,t\in {\mathbb Z}$. Let k be an algebraically closed field or a pseudo-finite field. Then ![]() $\psi_{n,s,t,r}$ is true for k.
$\psi_{n,s,t,r}$ is true for k.
Proof. Fix ![]() $n, s, t$ and r. If
$n, s, t$ and r. If ![]() $k= \overline{{\mathbb F}_p}$ for some prime p then
$k= \overline{{\mathbb F}_p}$ for some prime p then ![]() $\mathcal{G}(k)$ has the Honda property for every linear algebraic group
$\mathcal{G}(k)$ has the Honda property for every linear algebraic group ![]() $\mathcal{G}$ over k by Remark 1.3, so
$\mathcal{G}$ over k by Remark 1.3, so ![]() $\psi_{n,s,t,r}$ is true for k by
$\psi_{n,s,t,r}$ is true for k by ![]() $(\flat)$. Hence
$(\flat)$. Hence ![]() $\psi_{n,s,t,r}$ is true for any algebraically closed field k by Corollary 2.2. If k is a finite field then
$\psi_{n,s,t,r}$ is true for any algebraically closed field k by Corollary 2.2. If k is a finite field then ![]() $\mathcal{G}(k)$ has the Honda property for every linear algebraic group
$\mathcal{G}(k)$ has the Honda property for every linear algebraic group ![]() $\mathcal{G}$ over k by Theorem 1.1, so
$\mathcal{G}$ over k by Theorem 1.1, so ![]() $\psi_{n,s,t,r}$ is true for k by
$\psi_{n,s,t,r}$ is true for k by ![]() $(\flat)$. Hence
$(\flat)$. Hence ![]() $\psi_{n,s,t,r}$ is true for any pseudo-finite field.
$\psi_{n,s,t,r}$ is true for any pseudo-finite field.
Remark 2.4. We don’t know whether ![]() $\mathcal{G}(k)$ must satisfy the Honda property for
$\mathcal{G}(k)$ must satisfy the Honda property for ![]() $\mathcal{G}$ a linear algebraic group over an arbitrary field k. Tiersma has observed that if the conclusion of Theorem 1.2 holds for a field k then it holds for any algebraic field extension k ʹ of k. To see this, let
$\mathcal{G}$ a linear algebraic group over an arbitrary field k. Tiersma has observed that if the conclusion of Theorem 1.2 holds for a field k then it holds for any algebraic field extension k ʹ of k. To see this, let ![]() $\mathcal{G}'$ be a linear algebraic group over k ʹ. Let
$\mathcal{G}'$ be a linear algebraic group over k ʹ. Let ![]() $\alpha, \beta\in \mathcal{G}'(k')$. Let
$\alpha, \beta\in \mathcal{G}'(k')$. Let ![]() $\gamma= [\alpha, \beta]$ and let
$\gamma= [\alpha, \beta]$ and let ![]() $\delta\in \mathcal{G}'(k')$ such that
$\delta\in \mathcal{G}'(k')$ such that ![]() $\langle \delta\rangle= \langle \gamma\rangle$. There is a field k 1 such that
$\langle \delta\rangle= \langle \gamma\rangle$. There is a field k 1 such that ![]() $k\subseteq k_1\subseteq k'$,
$k\subseteq k_1\subseteq k'$, ![]() $k_1/k$ is finite,
$k_1/k$ is finite, ![]() $\mathcal{G}'$ descends to a k 1-group
$\mathcal{G}'$ descends to a k 1-group ![]() $\mathcal{G}_1$ and
$\mathcal{G}_1$ and ![]() $\alpha, \beta, \gamma, \delta\in \mathcal{G}_1(k_1)$. Let
$\alpha, \beta, \gamma, \delta\in \mathcal{G}_1(k_1)$. Let ![]() $\mathcal{G}$ be the Weil restriction
$\mathcal{G}$ be the Weil restriction ![]() $R_{k_1/k}(\mathcal{G}_1)$ [Reference Conrad, Gabber and Prasad4, A.5]. Then
$R_{k_1/k}(\mathcal{G}_1)$ [Reference Conrad, Gabber and Prasad4, A.5]. Then ![]() $\mathcal{G}(k)= \mathcal{G}_1(k_1)$. Since
$\mathcal{G}(k)= \mathcal{G}_1(k_1)$. Since ![]() $\mathcal{G}(k)$ satisfies the Honda property by assumption, the result follows.
$\mathcal{G}(k)$ satisfies the Honda property by assumption, the result follows.
Here is another situation where we obtain a positive result. Let G be a connected compact Lie group. Then every element of ![]() $[G,G]$ is a commutator [Reference Hofmann and Morris7, Theorem 6.55], and it follows that G has the Honda property. The link with linear algebraic groups is the following: if
$[G,G]$ is a commutator [Reference Hofmann and Morris7, Theorem 6.55], and it follows that G has the Honda property. The link with linear algebraic groups is the following: if ![]() ${\mathcal G}$ is a Zariski-connected real reductive algebraic group then
${\mathcal G}$ is a Zariski-connected real reductive algebraic group then ![]() $G:= {\mathcal G}({\mathbb R})$ is compact if and only if
$G:= {\mathcal G}({\mathbb R})$ is compact if and only if ![]() ${\mathcal G}$ is anisotropic, and in this case G is connected in the standard topology [Reference Borel1, V.24.6(c)(ii)]. A similar argument using [Reference Ree17, Theorem] shows that any connected reductive linear algebraic group over an algebraically closed field has the Honda property; this recovers a special case of Theorem 1.2(a).
${\mathcal G}$ is anisotropic, and in this case G is connected in the standard topology [Reference Borel1, V.24.6(c)(ii)]. A similar argument using [Reference Ree17, Theorem] shows that any connected reductive linear algebraic group over an algebraically closed field has the Honda property; this recovers a special case of Theorem 1.2(a).
3. Profinite groups
In this section, we prove Theorem 1.2(c); by a non-archimedean local field we mean either a finite extension of a p-adic field or the field of Laurent series ![]() ${\mathbb F}_q(\!(T)\!)$ in an indeterminate T for some prime power q. In fact, we prove a more general result for profinite groups. Recall that a topological group is profinite if and only if it is compact and Hausdorff and has a neighbourhood base at the identity consisting of open subgroups [Reference Dixon, du Sautoy, Mann and Segal6, Proposition 1.2].
${\mathbb F}_q(\!(T)\!)$ in an indeterminate T for some prime power q. In fact, we prove a more general result for profinite groups. Recall that a topological group is profinite if and only if it is compact and Hausdorff and has a neighbourhood base at the identity consisting of open subgroups [Reference Dixon, du Sautoy, Mann and Segal6, Proposition 1.2].
Proposition 3.1. Every profinite group has the Honda property.
Proof. Let G be a profinite group. Let Q be the set of finite-index normal subgroups of G. Let ![]() $\gamma, \delta\in G$ such that γ is a commutator and
$\gamma, \delta\in G$ such that γ is a commutator and ![]() $\langle \delta\rangle= \langle \gamma\rangle$. For
$\langle \delta\rangle= \langle \gamma\rangle$. For ![]() $N\in Q$, let
$N\in Q$, let ![]() $\pi_N\colon G\to G/N$ denote the canonical projection, and set
$\pi_N\colon G\to G/N$ denote the canonical projection, and set ![]() $C_N= \{(\sigma, \tau)\in G\times G\,|\,\pi_N(\delta)= [\pi_N(\sigma), \pi_N(\tau)]\}$, a closed subset of G × G. By Theorem 1.1, CN is non-empty for each
$C_N= \{(\sigma, \tau)\in G\times G\,|\,\pi_N(\delta)= [\pi_N(\sigma), \pi_N(\tau)]\}$, a closed subset of G × G. By Theorem 1.1, CN is non-empty for each ![]() $N\in Q$. If
$N\in Q$. If ![]() $N_1,\ldots, N_t\in Q$ then
$N_1,\ldots, N_t\in Q$ then ![]() $N_1\cap\cdots \cap N_t\in Q$ and
$N_1\cap\cdots \cap N_t\in Q$ and ![]() $C_{N_1\cap\cdots \cap N_t}= C_{N_1}\cap\cdots \cap C_{N_t}$; in particular,
$C_{N_1\cap\cdots \cap N_t}= C_{N_1}\cap\cdots \cap C_{N_t}$; in particular, ![]() $C_{N_1}\cap\cdots \cap C_{N_t}$ is non-empty. By the finite intersection property for compact spaces,
$C_{N_1}\cap\cdots \cap C_{N_t}$ is non-empty. By the finite intersection property for compact spaces,  $\bigcap_{N\in Q} C_N$ is non-empty, so we can pick an element
$\bigcap_{N\in Q} C_N$ is non-empty, so we can pick an element ![]() $(\sigma, \tau)$ from it. Then
$(\sigma, \tau)$ from it. Then ![]() $\pi_N(\delta)= [\pi_N(\sigma), \pi_N(\tau)]$ for all
$\pi_N(\delta)= [\pi_N(\sigma), \pi_N(\tau)]$ for all ![]() $N\in Q$. But
$N\in Q$. But  $\bigcap_{N\in Q} N= 1$ as G is profinite, so
$\bigcap_{N\in Q} N= 1$ as G is profinite, so ![]() $[\sigma, \tau]= \delta$ and we are done.
$[\sigma, \tau]= \delta$ and we are done.
Remark 3.2. Lenstra has observed that if G is profinite then a variation of the Honda property holds: if ![]() $\gamma, \delta\in G$, γ is a commutator and the closures of
$\gamma, \delta\in G$, γ is a commutator and the closures of ![]() $\langle \gamma\rangle$ and
$\langle \gamma\rangle$ and ![]() $\langle \delta\rangle$ are equal then δ is also a commutator. The argument is very similar to the proof of Proposition 3.1.
$\langle \delta\rangle$ are equal then δ is also a commutator. The argument is very similar to the proof of Proposition 3.1.
Proof of Theorem 1.2(c)
Let F be a non-archimedean local field with associated norm ν and valuation ring k. Fix a uniformiser π. Let ![]() ${\mathcal G}$ be a linear algebraic group over k and let
${\mathcal G}$ be a linear algebraic group over k and let ![]() $G= {\mathcal G}(k)$. It is enough by Proposition 3.1 to show that G is profinite. By assumption, there is an embedding of
$G= {\mathcal G}(k)$. It is enough by Proposition 3.1 to show that G is profinite. By assumption, there is an embedding of ![]() ${\mathcal G}$ as a closed subgroup of SLn for some n. So G is a subgroup of
${\mathcal G}$ as a closed subgroup of SLn for some n. So G is a subgroup of ![]() ${\rm SL}_n(k)$ and there are polynomials
${\rm SL}_n(k)$ and there are polynomials ![]() $f_1,\ldots, f_t$ in n 2 variables over k for some
$f_1,\ldots, f_t$ in n 2 variables over k for some ![]() $t\in {\mathbb N}_0$ such that
$t\in {\mathbb N}_0$ such that  $G= \{a_{ij}\in k^{n^2}\,|\,f_i(a_{ij})= 0$ for
$G= \{a_{ij}\in k^{n^2}\,|\,f_i(a_{ij})= 0$ for ![]() $1\leq i\leq t\}$ (we need only finitely many polynomials as discrete valuation ringsare Noetherian). The operations of addition and multiplication on k are continuous; it follows easily that G is a closed subspace of
$1\leq i\leq t\}$ (we need only finitely many polynomials as discrete valuation ringsare Noetherian). The operations of addition and multiplication on k are continuous; it follows easily that G is a closed subspace of ![]() $k^{n^2}$ with respect to the topology on
$k^{n^2}$ with respect to the topology on ![]() $k^{n^2}$ induced by ν, and the group operations on G are continuous. Hence G is a compact topological group. The open subgroups
$k^{n^2}$ induced by ν, and the group operations on G are continuous. Hence G is a compact topological group. The open subgroups ![]() $G_n:= \{g\in G\,|\,g= 1 \mod \pi^n\}$ form a neighbourhood base at the identity. It follows that G is profinite, as required.
$G_n:= \{g\in G\,|\,g= 1 \mod \pi^n\}$ form a neighbourhood base at the identity. It follows that G is profinite, as required.
Acknowledgements
I’m grateful to Hendrik Lenstra for introducing me to the Honda property, for stimulating discussions and for sharing a draft of his preprint [Reference Lenstra9] with me. I’m grateful to Hendrik and to Samuel Tiersma for comments on earlier drafts of this note. I’d also like to thank the referees for some comments and corrections, and the Edinburgh Mathematical Society for supporting Lenstra’s visit to Aberdeen.
Competing interests
The author declares none.