Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T18:52:54.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Open surfaces with congruent geodesics

Published online by Cambridge University Press:  20 January 2009

Charlambos Charitos
Charlambos Charitos
Affiliation:
University of CreteDepartment of MathematicsIraklion P. O. Box 1470, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to prove the Theorem: Let M be a complete non compact surface without boundary in the euclidean space 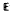3. We suppose that all geodesies of M are congruent. Then M is an affine plane in 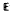3.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 38 , Issue 1 , February 1995 , pp. 179 - 183
Copyright
Copyright © Edinburgh Mathematical Society 1995

References

REFERENCES

1.Cartan, E., Sur des families remarquables d'hypersurfaces dans les espaces spheriques, Math. Z. (1939), 335–367.CrossRefGoogle Scholar
2.Charitos, C., Surfaces with Congruent Shadow-lines, Mathematika 37 (1990), 43–58.CrossRefGoogle Scholar
3.Charitos, C. and Pamfilos, P., Surfaces with Isometric Geodesies, Proc. Edinburgh Math. Soc. 34 (1991), 359–362.CrossRefGoogle Scholar
4.Ballman, W., Ghys, E., Haefliger, A., de la Harpe, P., Salem, E., Strebel, R., Troyanov, M., Sur les groupes hyperboliques d'après Gromov (Seminaire Berne édité par E. Ghys et P. de la Harpe, Birkhauser, 1990).Google Scholar
5.Hirsch, M., Differential Topology (Springer-Verlag, 1976).CrossRefGoogle Scholar
6.Mani, P., Fields of planar bodies tangent to spheres, Monatsh. Math. 74 (1970) 145–149.CrossRefGoogle Scholar
7.Ryan, P., Homogeneity and some curvature conditions for hyperfurfaces, Tôhoku Math. J. 21 (1969), 363–388.CrossRefGoogle Scholar
8. [S1], [S2] Spivak, M., A Comprehensive Introduction to Diff. Geometry, vol III.Google Scholar
9. vol IV (Publish or Perish, 1975).Google Scholar
10.Suss, [Su] W.Kennzeichende Eigenschaften der Kugel als Folgerung eines Brouwersche Fixtpunktsatzes, Comment. Math. Helv. 20 (1947), 61–64.CrossRefGoogle Scholar