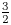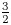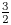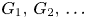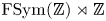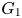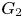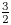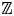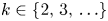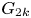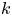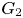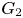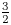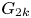1. Introduction
A group $G$![]() is $\frac 32$
is $\frac 32$![]() -generated if for every non-trivial $g\in G$
-generated if for every non-trivial $g\in G$![]() there exists an $h\in G$
there exists an $h\in G$![]() such that $\langle g,\, h\rangle =G$
such that $\langle g,\, h\rangle =G$![]() . This name was chosen because the property is stronger than being $2$
. This name was chosen because the property is stronger than being $2$![]() -generated but is weaker than being cyclic. A natural generalization of this is the notion of spread, introduced in [Reference Brenner and Wiegold2]. The spread of a group $G$
-generated but is weaker than being cyclic. A natural generalization of this is the notion of spread, introduced in [Reference Brenner and Wiegold2]. The spread of a group $G$![]() , denoted by $s(G)$
, denoted by $s(G)$![]() , is the supremum of those $k\in \mathbb {N}\cup \{0\}$
, is the supremum of those $k\in \mathbb {N}\cup \{0\}$![]() such that, for every $g_1,\, \ldots,\, g_k \in G\setminus \{1\}$
such that, for every $g_1,\, \ldots,\, g_k \in G\setminus \{1\}$![]() , there exists an $h\in G$
, there exists an $h\in G$![]() with
with
This notion has attracted significant attention for finite groups, e.g. [Reference Brenner and Wiegold2–Reference Breuer, Guralnick and Kantor4, Reference Burness and Harper8, Reference Burness, Guralnick and Harper9, Reference Guralnick and Kantor16, Reference Guralnick and Shalev17]. But the first paper on spread for infinite groups, [Reference Donoven and Harper13], only recently appeared. They showed that the Higman–Thompson and Brin–Thompson groups are $\frac 32$![]() -generated, i.e. have spread at least 1. They also posed many interesting questions, which we investigate here. The following lemma is a good place to start.
-generated, i.e. have spread at least 1. They also posed many interesting questions, which we investigate here. The following lemma is a good place to start.
Lemma If $G$![]() is $\frac 32$
is $\frac 32$![]() -generated, then every proper quotient of $G$
-generated, then every proper quotient of $G$![]() is cyclic.
is cyclic.
Proof. Let $H\lhd G$![]() be chosen so that the quotient of $G$
be chosen so that the quotient of $G$![]() by $H$
by $H$![]() is not cyclic, and let $h\in H\setminus \{1\}$
is not cyclic, and let $h\in H\setminus \{1\}$![]() . Then $\langle g,\, h\rangle \ne G$
. Then $\langle g,\, h\rangle \ne G$![]() for every $g\in G$
for every $g\in G$![]() .
.
In the case of finite groups, there has been an exceptional effort [Reference Burness and Guest6, Reference Burness, Guralnick and Harper9, Reference Harper18, 19] to prove the converse of this statement, which was first conjectured in [Reference Breuer, Guralnick and Kantor4] and eventually completed in [Reference Burness, Guralnick and Harper9]. For infinite groups, the converse to the above lemma is false for a trivial reason: the existence of infinite simple groups that are not 2-generated. Note that there exist finitely generated, but not $2$![]() -generated, infinite simple groups, as shown in [Reference Guba14]. This leads us to the first question raised in [Reference Donoven and Harper13].
-generated, infinite simple groups, as shown in [Reference Guba14]. This leads us to the first question raised in [Reference Donoven and Harper13].
Question 1 Is there a 2-generated group with no non-cyclic proper quotients that is not $\frac 32$![]() -generated?
-generated?
The answer to this is yes, as indicated by our first theorem. The groups considered are all finite index in the second Houghton group. This is the group $\operatorname {FSym}(\mathbb {Z})\rtimes \langle t\rangle$![]() , where $\operatorname {FSym}(\mathbb {Z})$
, where $\operatorname {FSym}(\mathbb {Z})$![]() consists of all bijections of $\mathbb {Z}$
consists of all bijections of $\mathbb {Z}$![]() which move only finitely many points, and $t$
which move only finitely many points, and $t$![]() is the translation map sending $z$
is the translation map sending $z$![]() to $z+1$
to $z+1$![]() for all $z\in \mathbb {Z}$
for all $z\in \mathbb {Z}$![]() . Then $\operatorname {FSym}(\mathbb {Z})$
. Then $\operatorname {FSym}(\mathbb {Z})$![]() contains $\operatorname {Alt}(\mathbb {Z})$
contains $\operatorname {Alt}(\mathbb {Z})$![]() , which consists of exactly those permutations which are even. We consider, for $k\in \mathbb {N}$
, which consists of exactly those permutations which are even. We consider, for $k\in \mathbb {N}$![]() , the groups $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle$
, the groups $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle$![]() . These groups were introduced in [Reference Burillo, Cleary, Martino and Röver5], and, because the second Houghton group is not finitely presented, neither are any of the groups $G_k$
. These groups were introduced in [Reference Burillo, Cleary, Martino and Röver5], and, because the second Houghton group is not finitely presented, neither are any of the groups $G_k$![]() .
.
Theorem 4.1 The groups $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle,$![]() indexed over the naturals, satisfy:
indexed over the naturals, satisfy:
(i) for every $k \in \mathbb {N}$
 , the group $G_k$
, the group $G_k$ is 2-generated;
is 2-generated;(ii) for every $k \in \mathbb {N}$
 , every proper quotient of $G_k$
, every proper quotient of $G_k$ is cyclic; but
is cyclic; but(iii) for every $k \in \{3,\, 4,\, \ldots \},$
 the group $G_k$
the group $G_k$ is not $\frac 32$
is not $\frac 32$ -generated, i.e., $s(G_k)=0$
-generated, i.e., $s(G_k)=0$ .
.
For (i), we make a careful choice of elements to generate each $G_k$![]() . Although the groups appearing in Theorem 4.1 are not simple, a short argument shows that they have $\operatorname {Alt}(\mathbb {Z})$
. Although the groups appearing in Theorem 4.1 are not simple, a short argument shows that they have $\operatorname {Alt}(\mathbb {Z})$![]() as a unique minimal normal subgroup. This ensures that (ii) holds. Then (iii) easily follows from $(1\;2\;3)\in G_k$
as a unique minimal normal subgroup. This ensures that (ii) holds. Then (iii) easily follows from $(1\;2\;3)\in G_k$![]() not being part of a generating pair. Also, given any $k\in \{2,\, 3,\, \ldots \}$
not being part of a generating pair. Also, given any $k\in \{2,\, 3,\, \ldots \}$![]() , note that $G_{2k}$
, note that $G_{2k}$![]() is index $k$
is index $k$![]() in $G_2$
in $G_2$![]() but $s(G_2)>0$
but $s(G_2)>0$![]() whilst $s(G_{2k})=0$
whilst $s(G_{2k})=0$![]() . We then show that these groups are in some sense ‘not far’ from having infinite spread, with the obstruction coming from the finite order elements.
. We then show that these groups are in some sense ‘not far’ from having infinite spread, with the obstruction coming from the finite order elements.
Theorem 4.4 Let $k,\, n \in \mathbb {N}$![]() and $g_1,\, \ldots,\, g_n \in G_k\setminus \operatorname {Alt}(\mathbb {Z})$
and $g_1,\, \ldots,\, g_n \in G_k\setminus \operatorname {Alt}(\mathbb {Z})$![]() . Then there exists an $h\in [t^{k}]\subset G_k$
. Then there exists an $h\in [t^{k}]\subset G_k$![]() such that $\langle g_1,\, h\rangle =\ldots =\langle g_n,\, h\rangle =G_k$
such that $\langle g_1,\, h\rangle =\ldots =\langle g_n,\, h\rangle =G_k$![]() .
.
We then investigate the other questions of [Reference Donoven and Harper13], which require additional notions. Given a group $G$![]() , let us say that the spread on $X\subseteq G$
, let us say that the spread on $X\subseteq G$![]() is the supremum of those $k\in \mathbb {N}\cup \{0\}$
is the supremum of those $k\in \mathbb {N}\cup \{0\}$![]() such that for any $g_1,\, \ldots,\, g_k\in G$
such that for any $g_1,\, \ldots,\, g_k\in G$![]() there exists an $h \in X$
there exists an $h \in X$![]() so that
so that
Although the author is unaware of it having been used, the notation $s_X(G)$![]() appears natural in this context. If there is a set $X$
appears natural in this context. If there is a set $X$![]() such that $s_X(G)\geqslant 1$
such that $s_X(G)\geqslant 1$![]() , then $X$
, then $X$![]() is called a total dominating set of $G$
is called a total dominating set of $G$![]() . We can then define the uniform spread of $G$
. We can then define the uniform spread of $G$![]() as the supremum of $\{s_C(G)\;:\;C$
as the supremum of $\{s_C(G)\;:\;C$![]() a conjugacy class of $G\}$
a conjugacy class of $G\}$![]() , and denote this by $u(G)$
, and denote this by $u(G)$![]() . The concept of uniform spread was introduced in [Reference Breuer, Guralnick and Kantor4]; both [Reference Burness and Harper7, Reference Burness and Harper8] provide further interesting results for finite groups. Note that $u(G)\leqslant s(G)$
. The concept of uniform spread was introduced in [Reference Breuer, Guralnick and Kantor4]; both [Reference Burness and Harper7, Reference Burness and Harper8] provide further interesting results for finite groups. Note that $u(G)\leqslant s(G)$![]() by definition.
by definition.
Proposition 5.5 No finite total dominating set exists for $G_1$![]() or $G_2$
or $G_2$![]() .
.
Since all of the elements we use for $G_1$![]() lie in $[t]$
lie in $[t]$![]() and the elements we use for $G_2$
and the elements we use for $G_2$![]() lie in $[t^{2}]$
lie in $[t^{2}]$![]() , our computations for the spread of $G_1$
, our computations for the spread of $G_1$![]() and $G_2$
and $G_2$![]() provide information about the uniform spread of these groups. Note that [Reference Burness, Guralnick and Harper9] also showed that no finite group $G$
provide information about the uniform spread of these groups. Note that [Reference Burness, Guralnick and Harper9] also showed that no finite group $G$![]() has $s(G)=1$
has $s(G)=1$![]() , which was open from 1975 having been discussed in [Reference Brenner and Wiegold2]. Deciding whether this is also the case for infinite groups is [Reference Donoven and Harper13, Question 2], but we see that $G_1$
, which was open from 1975 having been discussed in [Reference Brenner and Wiegold2]. Deciding whether this is also the case for infinite groups is [Reference Donoven and Harper13, Question 2], but we see that $G_1$![]() and $G_2$
and $G_2$![]() do not resolve this question.
do not resolve this question.
Theorem 6.1 Let $G_1=\langle (1\;2\;3),\, t\rangle$![]() and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$
and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$![]() . Then $u(G_1)\geqslant 2,$
. Then $u(G_1)\geqslant 2,$![]() $u(G_2)\geqslant 2,$
$u(G_2)\geqslant 2,$![]() $s(G_1)\leqslant 9,$
$s(G_1)\leqslant 9,$![]() and $s(G_2)\leqslant 9$
and $s(G_2)\leqslant 9$![]() .
.
Note that $G_1$![]() and $G_2$
and $G_2$![]() are the first infinite groups known to have finite positive spread, and the first to be shown to have spread at least 2 (other than $\mathbb {Z}$
are the first infinite groups known to have finite positive spread, and the first to be shown to have spread at least 2 (other than $\mathbb {Z}$![]() and the Tarski monsters, which have infinite spread).
and the Tarski monsters, which have infinite spread).
We thank Benjamin Barrett, Scott Harper, and Jeremy Rickard for helpful conversations regarding the proof of the following lemma, which significantly narrows the search for $\frac 32$![]() -generated groups. Harry Petyt has also pointed out that the residually finite condition can be weakened (by not requiring the quotient to be finite).
-generated groups. Harry Petyt has also pointed out that the residually finite condition can be weakened (by not requiring the quotient to be finite).
Lemma 1.1 Let $G$![]() be infinite, residually finite, and have every proper quotient cyclic. Then $G=\mathbb {Z}$
be infinite, residually finite, and have every proper quotient cyclic. Then $G=\mathbb {Z}$![]() .
.
Proof. Our proof involves three parts: that the group is abelian; that the group is finitely generated; and that it must be $\mathbb {Z}$![]() .
.
Assume there exist $a,\, b \in G$![]() such that $[a,\, b]$
such that $[a,\, b]$![]() , the commutator of $a$
, the commutator of $a$![]() and $b$
and $b$![]() , is non-trivial. Using that $G$
, is non-trivial. Using that $G$![]() is residually finite, there must exist a non-trivial normal subgroup $N$
is residually finite, there must exist a non-trivial normal subgroup $N$![]() of $G$
of $G$![]() with $[a,\, b]\not \in N$
with $[a,\, b]\not \in N$![]() . But then the images of $a$
. But then the images of $a$![]() and $b$
and $b$![]() in the quotient of $G$
in the quotient of $G$![]() by $N$
by $N$![]() must be non-trivial, and $G/N$
must be non-trivial, and $G/N$![]() is non-abelian and so not cyclic.
is non-abelian and so not cyclic.
Now let $x \in G\setminus \{1\}$![]() . Then $G/\langle x\rangle$
. Then $G/\langle x\rangle$![]() is cyclic, and so is generated by some $y$
is cyclic, and so is generated by some $y$![]() . Taking a preimage $y'$
. Taking a preimage $y'$![]() of $y$
of $y$![]() implies that $G=\langle x,\, y'\rangle$
implies that $G=\langle x,\, y'\rangle$![]() . Thus, $G$
. Thus, $G$![]() is finitely generated.
is finitely generated.
Since $G$![]() is a finitely generated abelian group, $G=A\times \mathbb {Z}^{n}$
is a finitely generated abelian group, $G=A\times \mathbb {Z}^{n}$![]() for some finite abelian group $A$
for some finite abelian group $A$![]() and $n \in \mathbb {N}\cup \{0\}$
and $n \in \mathbb {N}\cup \{0\}$![]() . If $n=0$
. If $n=0$![]() , then $G$
, then $G$![]() is finite. Finally, using the condition on quotients, it is clear that $n=1$
is finite. Finally, using the condition on quotients, it is clear that $n=1$![]() and $A$
and $A$![]() must be trivial.
must be trivial.
2. The Houghton groups
For each $n\in \mathbb {N}$![]() , the Houghton group $H_n$
, the Houghton group $H_n$![]() acts on the set $X_n:=\{1,\, \ldots,\, n\}\times \mathbb {N}$
acts on the set $X_n:=\{1,\, \ldots,\, n\}\times \mathbb {N}$![]() in a way that is ‘eventually a translation’. This paper deals exclusively with subgroups of $H_2$
in a way that is ‘eventually a translation’. This paper deals exclusively with subgroups of $H_2$![]() , and so it is this group – and a particularly nice representation of it – that we introduce here. For a more in-depth introduction, see, for example, [Reference Cox11].
, and so it is this group – and a particularly nice representation of it – that we introduce here. For a more in-depth introduction, see, for example, [Reference Cox11].
Definition 2.1 Given $X\ne \emptyset$![]() , let $\operatorname {Sym}(X)$
, let $\operatorname {Sym}(X)$![]() denote the group of all bijections on $X$
denote the group of all bijections on $X$![]() . For any $g\in \operatorname {Sym}(X)$
. For any $g\in \operatorname {Sym}(X)$![]() , we then define $\operatorname {supp}(g):=\{x\in X : (x)g\ne x\}$
, we then define $\operatorname {supp}(g):=\{x\in X : (x)g\ne x\}$![]() , which is often called the support of $g$
, which is often called the support of $g$![]() . Let $\operatorname {FSym}(X)$
. Let $\operatorname {FSym}(X)$![]() consist of those $g\in \operatorname {Sym}(X)$
consist of those $g\in \operatorname {Sym}(X)$![]() with $|\operatorname {supp}(g)|<\infty$
with $|\operatorname {supp}(g)|<\infty$![]() , and let $\operatorname {Alt}(X)\leqslant \operatorname {FSym}(X)$
, and let $\operatorname {Alt}(X)\leqslant \operatorname {FSym}(X)$![]() consist of all even permutations.
consist of all even permutations.
Note that, if $|X|=n$![]() , then $\operatorname {Sym}(X)=\operatorname {FSym}(X)\cong S_n$
, then $\operatorname {Sym}(X)=\operatorname {FSym}(X)\cong S_n$![]() and $\operatorname {Alt}(X)\cong A_n$
and $\operatorname {Alt}(X)\cong A_n$![]() .
.
Notation Let $t\in \operatorname {Sym}(\mathbb {Z})$![]() be defined as $t: z\mapsto z+1$
be defined as $t: z\mapsto z+1$![]() for all $z \in \mathbb {Z}$
for all $z \in \mathbb {Z}$![]() .
.
Definition 2.2 The group $H_2$![]() , sometimes called the second Houghton group, is the group $\operatorname {FSym}(\mathbb {Z})\rtimes \langle t\rangle$
, sometimes called the second Houghton group, is the group $\operatorname {FSym}(\mathbb {Z})\rtimes \langle t\rangle$![]() .
.
A first important observation is that conjugacy in this group, being a subgroup of $\operatorname {Sym}(\mathbb {Z})$![]() , is easy to understand: conjugation by $g\in \operatorname {Sym}(\mathbb {Z})$
, is easy to understand: conjugation by $g\in \operatorname {Sym}(\mathbb {Z})$![]() changes the support exactly by how it acts on $\mathbb {Z}$
changes the support exactly by how it acts on $\mathbb {Z}$![]() , e.g. $g^{-1}(a\;b\;c)g=((a)g\;(b)g\;(c)g)$
, e.g. $g^{-1}(a\;b\;c)g=((a)g\;(b)g\;(c)g)$![]() . A commonly used generating set is then $\{(0\;1),\, t\}$
. A commonly used generating set is then $\{(0\;1),\, t\}$![]() . From [Reference Guba and Sapir15], $H_2$
. From [Reference Guba and Sapir15], $H_2$![]() has exponential conjugacy growth.
has exponential conjugacy growth.
To add clarity to our arguments, we also remark here that elements in $H_2$![]() do indeed ‘eventually act as a translation’, meaning that their infinite orbits have a simple structure. The following is based on [Reference Antolín, Burillo and Martino1, Prop. 2.6].
do indeed ‘eventually act as a translation’, meaning that their infinite orbits have a simple structure. The following is based on [Reference Antolín, Burillo and Martino1, Prop. 2.6].
Lemma 2.3 Let $g\in H_2$![]() and $z\in \mathbb {Z}$
and $z\in \mathbb {Z}$![]() . If $\{(z)g^{m}\;:\;m\in \mathbb {Z}\}$
. If $\{(z)g^{m}\;:\;m\in \mathbb {Z}\}$![]() is infinite, then it differs only on finitely many points from a set of the form
is infinite, then it differs only on finitely many points from a set of the form
for some $d_1,\, d_2,\, r_1,\, r_2\in \mathbb {N}$![]() .
.
Proof. Note that $g=\sigma t^{c}$![]() for some $\sigma \in \operatorname {FSym}(\mathbb {Z})$
for some $\sigma \in \operatorname {FSym}(\mathbb {Z})$![]() and $c\in \mathbb {Z}$
and $c\in \mathbb {Z}$![]() . Thus, if $x\not \in \operatorname {supp}(\sigma )$
. Thus, if $x\not \in \operatorname {supp}(\sigma )$![]() , then the result follows by considering $\{(x)g^{m}\;:\;m\in \mathbb {N}\}$
, then the result follows by considering $\{(x)g^{m}\;:\;m\in \mathbb {N}\}$![]() and $\{(x)g^{-m}\;:\;m\in \mathbb {N}\}$
and $\{(x)g^{-m}\;:\;m\in \mathbb {N}\}$![]() . Then $d_1$
. Then $d_1$![]() and $d_2$
and $d_2$![]() are both equal to $c$
are both equal to $c$![]() in this case. Now, if $y\in \operatorname {supp}(\sigma )$
in this case. Now, if $y\in \operatorname {supp}(\sigma )$![]() , either $y$
, either $y$![]() lies on a finite orbit or one of the infinite orbits already described.
lies on a finite orbit or one of the infinite orbits already described.
Remark 2.4 Lemma 2.3 means that for each $g\in H_2$![]() there are numbers $k\in \mathbb {Z}$
there are numbers $k\in \mathbb {Z}$![]() and $z\in \mathbb {N}$
and $z\in \mathbb {N}$![]() such that $(x)g=x+k$
such that $(x)g=x+k$![]() for every $x\in \mathbb {Z}\setminus \{-z,\, \ldots,\, z\}$
for every $x\in \mathbb {Z}\setminus \{-z,\, \ldots,\, z\}$![]() .
.
3. On a family of two generated subgroups of $H_2$
The groups we will use were introduced in [Reference Burillo, Cleary, Martino and Röver5] and are all finite index in $H_2$![]() .
.
Definition 3.1 For each $k \in \mathbb {N}$![]() , let $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle$
, let $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle$![]() .
.
It follows from [Reference Cox11, Lem. 5.9] and [Reference Cox12, Lem. 2.4] that $\operatorname {Aut}(G_k)\cong H_{2k}\rtimes (S_k\wr C_2)$![]() , where the elements in $S_k\wr C_2$
, where the elements in $S_k\wr C_2$![]() relate to isometrically permuting the $2k$
relate to isometrically permuting the $2k$![]() rays of $X_{2k}$
rays of $X_{2k}$![]() . This means that $G_m\cong G_n$
. This means that $G_m\cong G_n$![]() only if $m=n$
only if $m=n$![]() .
.
Remark 3.2 Since $\operatorname {Alt}(\mathbb {Z})$![]() is an infinite simple group, $G_k$
is an infinite simple group, $G_k$![]() is not residually finite.
is not residually finite.
The following allows us to see that the groups $G_k$![]() have the property on proper quotients that we desire.
have the property on proper quotients that we desire.
Lemma 3.3 Cox [Reference Cox12, Prop. 2.5]
Let $\operatorname {Alt}(\mathbb {Z})\leqslant G\leqslant \operatorname {Sym}(\mathbb {Z})$![]() . Then $G$
. Then $G$![]() has $\operatorname {Alt}(\mathbb {Z})$
has $\operatorname {Alt}(\mathbb {Z})$![]() as a unique minimal normal subgroup.
as a unique minimal normal subgroup.
Lemma 3.4 Let $k\in \mathbb {N}$![]() . Then every proper quotient of $G_k$
. Then every proper quotient of $G_k$![]() is cyclic.
is cyclic.
Proof. Let $N$![]() be a non-trivial normal subgroup of $G_k$
be a non-trivial normal subgroup of $G_k$![]() . Then $\operatorname {Alt}(\mathbb {Z})\leqslant N$
. Then $\operatorname {Alt}(\mathbb {Z})\leqslant N$![]() , and so
, and so
i.e. $G_{k}/N$![]() is a quotient of $G_{k}/\operatorname{Alt}(\mathbb{Z})\cong \langle t^{k}\rangle$
is a quotient of $G_{k}/\operatorname{Alt}(\mathbb{Z})\cong \langle t^{k}\rangle$![]() , and hence cyclic.
, and hence cyclic.
We now show, for each $k\in \mathbb {N}$![]() , that the group $G_k$
, that the group $G_k$![]() is $2$
is $2$![]() -generated.
-generated.
Remark 3.5 Computations show that $G_1=\langle (1\;2\;3),\, t\rangle$![]() and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$
and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$![]() .
.
The following result is essentially [Reference Cox10, Lem. 3.2].
Notation For any $k\in \mathbb {N}$![]() , let $\Omega _k=\{1,\, 2,\, \ldots,\, k\}$
, let $\Omega _k=\{1,\, 2,\, \ldots,\, k\}$![]() .
.
Lemma 3.6 Let $k\in \{3,\, 4,\, \ldots \}$![]() . Then $G_k$
. Then $G_k$![]() is generated by $\operatorname {Alt}(\Omega _{2k}) \cup \{t^{k}\}$
is generated by $\operatorname {Alt}(\Omega _{2k}) \cup \{t^{k}\}$![]() .
.
Proof. We will show that all $3$![]() -cycles in $\operatorname {Alt}(\mathbb {Z})$
-cycles in $\operatorname {Alt}(\mathbb {Z})$![]() lie in $\langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$
lie in $\langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$![]() . We only need to construct those $3$
. We only need to construct those $3$![]() -cycles with support in $\mathbb {N}$
-cycles with support in $\mathbb {N}$![]() , since for any $\sigma \in \operatorname {Alt}(\mathbb {Z})$
, since for any $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() there is an $n \in \mathbb {N}$
there is an $n \in \mathbb {N}$![]() such that $\operatorname {supp}(t^{-kn}\sigma t^{kn})\subset \mathbb {N}$
such that $\operatorname {supp}(t^{-kn}\sigma t^{kn})\subset \mathbb {N}$![]() . Moreover, $\{(1\;2\;m)\;:\;m\geqslant 3\}$
. Moreover, $\{(1\;2\;m)\;:\;m\geqslant 3\}$![]() generates $\operatorname {Alt}(\mathbb {N})$
generates $\operatorname {Alt}(\mathbb {N})$![]() since for any distinct $m_1,\, m_2,\, m_3\in \mathbb {N}$
since for any distinct $m_1,\, m_2,\, m_3\in \mathbb {N}$![]() we have $(1\;2\;m_1)(1\;2\;m_2)^{-1}=(2\;m_1\;m_2)$
we have $(1\;2\;m_1)(1\;2\;m_2)^{-1}=(2\;m_1\;m_2)$![]() and $(1\;2\;m_3)^{-1}(2\;m_1\;m_2)(1\;2\;m_3)=(m_1\;m_2\;m_3)$
and $(1\;2\;m_3)^{-1}(2\;m_1\;m_2)(1\;2\;m_3)=(m_1\;m_2\;m_3)$![]() .
.
By definition, $(1\;2\;m)\in \operatorname {Alt}(\Omega _{2k})$![]() for $m=3,\, \ldots,\, 2k$
for $m=3,\, \ldots,\, 2k$![]() . To use induction on $n$
. To use induction on $n$![]() , let us assume, for each $r\in \{1,\, \ldots,\, k\}$
, let us assume, for each $r\in \{1,\, \ldots,\, k\}$![]() , that $(1,\, 2,\, nk+r)\in \langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$
, that $(1,\, 2,\, nk+r)\in \langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$![]() . Thus, we want to show that $\langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$
. Thus, we want to show that $\langle \operatorname {Alt}(\Omega _{2k}),\, t^{k}\rangle$![]() also contains $(1,\, 2,\, (n+1)k+r)$
also contains $(1,\, 2,\, (n+1)k+r)$![]() . Clearly $(r,\, r+1,\, r+k)\in \langle \Omega _{2k},\, t^{k}\rangle$
. Clearly $(r,\, r+1,\, r+k)\in \langle \Omega _{2k},\, t^{k}\rangle$![]() . Let
. Let
Conjugating $(1,\, 2,\, nk+r)$![]() by $\omega ^{-1}$
by $\omega ^{-1}$![]() yields the required element $(1,\, 2,\, (n+1)k+r)$
yields the required element $(1,\, 2,\, (n+1)k+r)$![]() .
.
Lemma 3.7 Let $k \in \{3,\, 4,\, \ldots \}$![]() . Then $G_k$
. Then $G_k$![]() is 2-generated.
is 2-generated.
Proof. Our aim is to reduce to the previous lemma. From the assumption that $k\geqslant 3$![]() , all $3$
, all $3$![]() -cycles in $\operatorname {Alt}(\Omega _{2k})$
-cycles in $\operatorname {Alt}(\Omega _{2k})$![]() are conjugate. Our generating set will consist of $t^{k}$
are conjugate. Our generating set will consist of $t^{k}$![]() and an element $\alpha \in \operatorname {Alt}(\mathbb {Z})$
and an element $\alpha \in \operatorname {Alt}(\mathbb {Z})$![]() .
.
Let $n=\binom {2k}{3}$![]() and let $\omega _1,\, \ldots,\, \omega _n$
and let $\omega _1,\, \ldots,\, \omega _n$![]() be a choice of distinct $3$
be a choice of distinct $3$![]() -cycles in $\operatorname {Alt}(\Omega _{2k})$
-cycles in $\operatorname {Alt}(\Omega _{2k})$![]() with $\omega _i\ne \omega _j^{-1}$
with $\omega _i\ne \omega _j^{-1}$![]() for every $i,\,j \in \{1,\, \ldots,\, n\}$
for every $i,\,j \in \{1,\, \ldots,\, n\}$![]() . Thus $\langle \omega _1,\, \ldots,\, \omega _n\rangle =\operatorname {Alt}(\Omega _{2k})$
. Thus $\langle \omega _1,\, \ldots,\, \omega _n\rangle =\operatorname {Alt}(\Omega _{2k})$![]() . Set $\sigma _0=(1\;3)$
. Set $\sigma _0=(1\;3)$![]() and $\sigma _{n+1}=(2\;3)$
and $\sigma _{n+1}=(2\;3)$![]() and observe that $(\sigma _{n+1}^{-1}\sigma _0^{-1}\sigma _{n+1})\sigma _0=(1\;2\;3)$
and observe that $(\sigma _{n+1}^{-1}\sigma _0^{-1}\sigma _{n+1})\sigma _0=(1\;2\;3)$![]() . Now choose $\sigma _1,\, \ldots,\, \sigma _{n}\in \operatorname {Alt}(\Omega _{2k})$
. Now choose $\sigma _1,\, \ldots,\, \sigma _{n}\in \operatorname {Alt}(\Omega _{2k})$![]() such that for each $m\in \{1,\,\ldots,\, n\}$
such that for each $m\in \{1,\,\ldots,\, n\}$![]() we have $\sigma _m^{-1}(1\;2\;3)\sigma _m=\omega _m$
we have $\sigma _m^{-1}(1\;2\;3)\sigma _m=\omega _m$![]() .
.
Let $\alpha :=\prod _{i=0}^{n+1}t^{-2ik}\sigma _it^{2ik}$![]() and, for each $m\in \{1,\,\ldots,\, n+1\}$
and, for each $m\in \{1,\,\ldots,\, n+1\}$![]() , let $\beta _m:=t^{2mk}\alpha t^{-2mk}$
, let $\beta _m:=t^{2mk}\alpha t^{-2mk}$![]() . Then $\beta _{n+1}^{-1}\alpha ^{-1}\beta _{n+1}\alpha =\sigma _{n+1}^{-1}\sigma _0^{-1}\sigma _{n+1}\sigma _0=(1\;2\;3)$
. Then $\beta _{n+1}^{-1}\alpha ^{-1}\beta _{n+1}\alpha =\sigma _{n+1}^{-1}\sigma _0^{-1}\sigma _{n+1}\sigma _0=(1\;2\;3)$![]() and, for $m\in \{1,\, \ldots,\, n\}$
and, for $m\in \{1,\, \ldots,\, n\}$![]() , we have that $\beta _m^{-1}(1\;2\;3)\beta _m=\omega _m$
, we have that $\beta _m^{-1}(1\;2\;3)\beta _m=\omega _m$![]() . Hence $\langle \alpha,\, t^{k}\rangle =G_k$
. Hence $\langle \alpha,\, t^{k}\rangle =G_k$![]() .
.
Remark 3.8 By including an odd element in the choice of the $\sigma _1,\, \ldots,\, \sigma _n$![]() , we note that there exists $\alpha _k\in \operatorname {FSym}(\mathbb {Z})$
, we note that there exists $\alpha _k\in \operatorname {FSym}(\mathbb {Z})$![]() such that $\langle \operatorname {FSym}(\mathbb {Z}),\, t^{k}\rangle =\langle \alpha _k,\, t^{k}\rangle$
such that $\langle \operatorname {FSym}(\mathbb {Z}),\, t^{k}\rangle =\langle \alpha _k,\, t^{k}\rangle$![]() for every $k \in \{3,\, 4,\, \ldots \}$
for every $k \in \{3,\, 4,\, \ldots \}$![]() . Then $\langle \operatorname {FSym}(\mathbb {Z}),\, t^{2}\rangle =\langle \alpha _4,\, t^{2}\rangle$
. Then $\langle \operatorname {FSym}(\mathbb {Z}),\, t^{2}\rangle =\langle \alpha _4,\, t^{2}\rangle$![]() since $\operatorname {FSym}(\mathbb {Z})\leqslant \langle \alpha _4,\, t^{4}\rangle \leqslant \langle \alpha _4,\, t^{2}\rangle$
since $\operatorname {FSym}(\mathbb {Z})\leqslant \langle \alpha _4,\, t^{4}\rangle \leqslant \langle \alpha _4,\, t^{2}\rangle$![]() .
.
4. On the spread of the groups $G_k$ , where $k \in \mathbb {N}$
, where $k \in \mathbb {N}$
Now that we have defined our 2-generated groups, we can investigate their spread. Our first aim is to prove the following. Part (i) is Lemma 3.7 and part (ii) is Lemma 3.4.
Theorem 4.1 The groups $G_k:=\langle \operatorname {Alt}(\mathbb {Z}),\, t^{k}\rangle,$![]() indexed over the naturals, satisfy:
indexed over the naturals, satisfy:
(i) for every $k \in \mathbb {N},$
 the group $G_k$
the group $G_k$ is 2-generated;
is 2-generated;(ii) for every $k \in \mathbb {N},$
 every proper quotient of $G_k$
every proper quotient of $G_k$ is cyclic; but
is cyclic; but(iii) for every $k \in \{3,\, 4,\, \ldots \},$
 the group $G_k$
the group $G_k$ is not $\frac 32$
is not $\frac 32$ -generated, i.e., $s(G_k)=0$
-generated, i.e., $s(G_k)=0$ .
.
We show (iii) by dealing separately with the cases $k\geqslant 4$![]() and $k=3$
and $k=3$![]() .
.
Lemma 4.2 Let $k\in \{4,\, 5,\, \ldots \}$![]() . Then $G_k$
. Then $G_k$![]() has spread zero.
has spread zero.
Proof. We will show, given any $h \in G_k$![]() , that $\langle (1\;2\;3),\, h\rangle$
, that $\langle (1\;2\;3),\, h\rangle$![]() does not contain $\operatorname {Alt}(\mathbb {Z})$
does not contain $\operatorname {Alt}(\mathbb {Z})$![]() and so cannot equal $G_k$
and so cannot equal $G_k$![]() .
.
If $h\in \operatorname {Alt}(\mathbb {Z})$![]() , then $\langle (1\;2\;3),\, h\rangle$
, then $\langle (1\;2\;3),\, h\rangle$![]() is finite. Thus, without loss of generality, $h=\omega t^{n}$
is finite. Thus, without loss of generality, $h=\omega t^{n}$![]() where $\omega \in \operatorname {Alt}(\mathbb {Z})$
where $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() and $n \in k\mathbb {N}$
and $n \in k\mathbb {N}$![]() . From our description of the orbits of $H_2$
. From our description of the orbits of $H_2$![]() , we know that $h$
, we know that $h$![]() has at least $k$
has at least $k$![]() infinite orbits. Thus, $h$
infinite orbits. Thus, $h$![]() has an infinite orbit $\mathcal {O}_4$
has an infinite orbit $\mathcal {O}_4$![]() which does not intersect $\{1,\, 2,\, 3\}$
which does not intersect $\{1,\, 2,\, 3\}$![]() . Let $x\in \mathcal {O}_4$
. Let $x\in \mathcal {O}_4$![]() . Then the orbit of $x$
. Then the orbit of $x$![]() under $\langle (1\;2\;3),\, h\rangle$
under $\langle (1\;2\;3),\, h\rangle$![]() is $\mathcal {O}_4$
is $\mathcal {O}_4$![]() .
.
Lemma 4.3 The group $G_3$![]() has spread zero.
has spread zero.
Proof. With a similar approach to the previous lemma, we will show, given any $h \in G_3$![]() , that $\langle (1\;2\;3),\, h\rangle \ne G_3$
, that $\langle (1\;2\;3),\, h\rangle \ne G_3$![]() .
.
If $h\in \operatorname {Alt}(\mathbb {Z})$![]() , then $\langle (1\;2\;3),\, h\rangle$
, then $\langle (1\;2\;3),\, h\rangle$![]() is finite. Similarly, if $h=\omega t^{n}$
is finite. Similarly, if $h=\omega t^{n}$![]() where $\omega \in \operatorname {Alt}(\mathbb {Z})$
where $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() and $n\not \in \{3,\, -3\}$
and $n\not \in \{3,\, -3\}$![]() , then $|n|>3$
, then $|n|>3$![]() and the argument in the previous lemma proves the result. Thus, without loss of generality, $h=\omega t^{3}$
and the argument in the previous lemma proves the result. Thus, without loss of generality, $h=\omega t^{3}$![]() where $\omega \in \operatorname {Alt}(\mathbb {Z})$
where $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() .
.
Let $\mathcal {O}_1,\, \mathcal {O}_2$![]() , and $\mathcal {O}_3$
, and $\mathcal {O}_3$![]() denote the three infinite orbits of $h$
denote the three infinite orbits of $h$![]() . After relabelling, we can assume that $i \in \mathcal {O}_i$
. After relabelling, we can assume that $i \in \mathcal {O}_i$![]() for $i=1,\, 2,\, 3$
for $i=1,\, 2,\, 3$![]() (for if, say, $\mathcal {O}_3$
(for if, say, $\mathcal {O}_3$![]() did not contain a point from $\{1,\, 2,\, 3\}$
did not contain a point from $\{1,\, 2,\, 3\}$![]() , then we could run the argument from the previous lemma). Moreover, if $\mathbb {Z}\setminus (\mathcal {O}_1\cup \mathcal {O}_2\cup \mathcal {O}_3)=Y\ne \emptyset$
, then we could run the argument from the previous lemma). Moreover, if $\mathbb {Z}\setminus (\mathcal {O}_1\cup \mathcal {O}_2\cup \mathcal {O}_3)=Y\ne \emptyset$![]() , then the orbit of points in $Y$
, then the orbit of points in $Y$![]() under $\langle (1\;2\;3),\, h\rangle$
under $\langle (1\;2\;3),\, h\rangle$![]() is the same as the orbit of points in $Y$
is the same as the orbit of points in $Y$![]() under $\langle h\rangle$
under $\langle h\rangle$![]() . By construction, this orbit cannot be $\mathbb {Z}$
. By construction, this orbit cannot be $\mathbb {Z}$![]() , which contradicts that $\operatorname {Alt}(\mathbb {Z})\leqslant G_3$
, which contradicts that $\operatorname {Alt}(\mathbb {Z})\leqslant G_3$![]() acts transitively on $\mathbb {Z}$
acts transitively on $\mathbb {Z}$![]() . Then $\mathcal {O}_1\cup \mathcal {O}_2\cup \mathcal {O}_3=\mathbb {Z}$
. Then $\mathcal {O}_1\cup \mathcal {O}_2\cup \mathcal {O}_3=\mathbb {Z}$![]() , and by relabelling $\mathbb {Z}$
, and by relabelling $\mathbb {Z}$![]() we can assume that
we can assume that
and $(1\;2\;3)$![]() has been relabelled as $\sigma =(a_1\;a_2\;a_3)$
has been relabelled as $\sigma =(a_1\;a_2\;a_3)$![]() where $a_i \in \mathcal {O}_i$
where $a_i \in \mathcal {O}_i$![]() for $i=1,\, 2,\, 3$
for $i=1,\, 2,\, 3$![]() . But then $\langle (a_1\;a_2\;a_3),\, h\rangle \cong C_3\wr \mathbb {Z}$
. But then $\langle (a_1\;a_2\;a_3),\, h\rangle \cong C_3\wr \mathbb {Z}$![]() , since for every $m\in \mathbb {Z}\setminus \{0\}$
, since for every $m\in \mathbb {Z}\setminus \{0\}$![]() we have that $h^{-m}(a_1\;a_2\;a_3)h^{m}$
we have that $h^{-m}(a_1\;a_2\;a_3)h^{m}$![]() and $(a_1\;a_2\;a_3)$
and $(a_1\;a_2\;a_3)$![]() are disjoint. Therefore $\langle (a_1\;a_2\;a_3),\, h\rangle$
are disjoint. Therefore $\langle (a_1\;a_2\;a_3),\, h\rangle$![]() has an imprimitive action on $\mathbb {Z}$
has an imprimitive action on $\mathbb {Z}$![]() , and so cannot contain $\operatorname {Alt}(\mathbb {Z})$
, and so cannot contain $\operatorname {Alt}(\mathbb {Z})$![]() .
.
Notation For any $\omega \in \operatorname {FSym}(\mathbb {Z})$![]() , let $s_\omega :=\omega ^{-1}t\omega$
, let $s_\omega :=\omega ^{-1}t\omega$![]() .
.
The following intriguing observation tells us that the groups $G_k$![]() are, in some sense, not far from having infinite spread.
are, in some sense, not far from having infinite spread.
Theorem 4.4 Let $k,\, n \in \mathbb {N}$![]() and $g_1,\, \ldots,\, g_n \in G_k\setminus \operatorname {Alt}(\mathbb {Z})$
and $g_1,\, \ldots,\, g_n \in G_k\setminus \operatorname {Alt}(\mathbb {Z})$![]() . Then there exists an $h\in [t^{k}]\subset G_k$
. Then there exists an $h\in [t^{k}]\subset G_k$![]() such that $\langle g_1,\, h\rangle =\ldots =\langle g_n,\, h\rangle =G_k$
such that $\langle g_1,\, h\rangle =\ldots =\langle g_n,\, h\rangle =G_k$![]() .
.
Proof. Fix a $k \in \mathbb {N}$![]() . We start by taking powers of the $g_1,\, \ldots,\, g_n$
. We start by taking powers of the $g_1,\, \ldots,\, g_n$![]() so to obtain
so to obtain
for some $c\in k\mathbb {N}$![]() and $\omega _1,\, \ldots,\, \omega _n \in \operatorname {Alt}(\mathbb {Z})$
and $\omega _1,\, \ldots,\, \omega _n \in \operatorname {Alt}(\mathbb {Z})$![]() . Our aim is to show that there exists a $\sigma \in \operatorname {Alt}(\mathbb {Z})$
. Our aim is to show that there exists a $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() so that $s_{\sigma }^{k}$
so that $s_{\sigma }^{k}$![]() is a suitable choice for our element $h\in G_k$
is a suitable choice for our element $h\in G_k$![]() .
.
From Remark 2.4, there exists an $m\in \mathbb {N}$![]() such that for every $z\in \mathbb {Z}\setminus \{-m,\, \ldots,\, m\}$
such that for every $z\in \mathbb {Z}\setminus \{-m,\, \ldots,\, m\}$![]() and every $i\in \{1,\, \ldots,\, n\}$
and every $i\in \{1,\, \ldots,\, n\}$![]() we have $\omega _it^{-c}(z)=z-c$
we have $\omega _it^{-c}(z)=z-c$![]() . Fix an $i\in \{1,\, \ldots,\, n\}$
. Fix an $i\in \{1,\, \ldots,\, n\}$![]() . Let $\omega _i^{*}:=(\omega _it^{-c})^{2}t^{2c}$
. Let $\omega _i^{*}:=(\omega _it^{-c})^{2}t^{2c}$![]() so that $(\omega _it^{-c})^{2}=\omega _i^{*}t^{-2c}$
so that $(\omega _it^{-c})^{2}=\omega _i^{*}t^{-2c}$![]() . Then, for any $\sigma \in \operatorname {Alt}(\mathbb {Z})$
. Then, for any $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() ,
,
and we can choose $\sigma$![]() so that $\operatorname {supp}(\sigma )\cap \operatorname {supp}(t^{-2c}\sigma ^{-1}t^{2c})=\emptyset$
so that $\operatorname {supp}(\sigma )\cap \operatorname {supp}(t^{-2c}\sigma ^{-1}t^{2c})=\emptyset$![]() . Recall that $\Omega _{2c}=\{1,\, \ldots,\, 2c\}$
. Recall that $\Omega _{2c}=\{1,\, \ldots,\, 2c\}$![]() . We will choose $\sigma$
. We will choose $\sigma$![]() so that $\operatorname {supp}(\sigma )\cap \{-m,\, \ldots,\, m\}=\emptyset$
so that $\operatorname {supp}(\sigma )\cap \{-m,\, \ldots,\, m\}=\emptyset$![]() and
and
We now mimick the proof of Lemma 3.7 (with $\omega _it^{-c}$![]() taking the role of $t^{k}$
taking the role of $t^{k}$![]() ) and show that there exists $\sigma \in \operatorname {FSym}(\mathbb {Z})$
) and show that there exists $\sigma \in \operatorname {FSym}(\mathbb {Z})$![]() , with the conditions above, such that $\langle \omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma,\, \omega _it^{-c}\rangle$
, with the conditions above, such that $\langle \omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma,\, \omega _it^{-c}\rangle$![]() contains $\Lambda :=\{\alpha \in \operatorname {Alt}(\mathbb {Z})\;:\;\min (\operatorname {supp}(\alpha ))\geqslant m\}$
contains $\Lambda :=\{\alpha \in \operatorname {Alt}(\mathbb {Z})\;:\;\min (\operatorname {supp}(\alpha ))\geqslant m\}$![]() . Let $n=\binom {2c}{3}$
. Let $n=\binom {2c}{3}$![]() , pick a set of distinct $3$
, pick a set of distinct $3$![]() -cycles $\tau _1,\, \ldots,\, \tau _n$
-cycles $\tau _1,\, \ldots,\, \tau _n$![]() with support in $\Omega _{2c}$
with support in $\Omega _{2c}$![]() such that $\tau _i\ne \tau _j^{-1}$
such that $\tau _i\ne \tau _j^{-1}$![]() for any $i,\, j\in \{1,\, \ldots,\, n\}$
for any $i,\, j\in \{1,\, \ldots,\, n\}$![]() , and choose $\sigma _1,\, \ldots,\, \sigma _n$
, and choose $\sigma _1,\, \ldots,\, \sigma _n$![]() with support in $\Omega _{2c}$
with support in $\Omega _{2c}$![]() such that $\sigma _i^{-1}(1\;2\;3)\sigma _i=\tau _i$
such that $\sigma _i^{-1}(1\;2\;3)\sigma _i=\tau _i$![]() for $i=1,\, \ldots,\, n$
for $i=1,\, \ldots,\, n$![]() . Choose $\sigma$
. Choose $\sigma$![]() so that $t^{4c(m+i)}\sigma t^{-4c(m+i)}$
so that $t^{4c(m+i)}\sigma t^{-4c(m+i)}$![]() acts on $\Omega _{2c}$
acts on $\Omega _{2c}$![]() in the same way as $\sigma _i$
in the same way as $\sigma _i$![]() for $i=1,\, \ldots,\, n$
for $i=1,\, \ldots,\, n$![]() , and moreover make $\sigma$
, and moreover make $\sigma$![]() act on $\Omega _{2c}t^{-4cm}$
act on $\Omega _{2c}t^{-4cm}$![]() and $\Omega _{2c}t^{4c(m+n+1)}$
and $\Omega _{2c}t^{4c(m+n+1)}$![]() in such a way that there exists $d\in \mathbb {N}$
in such a way that there exists $d\in \mathbb {N}$![]() so that the commutator of $(\omega _it^{-c})^{d}(\omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma )(\omega _it^{-c})^{-d}$
so that the commutator of $(\omega _it^{-c})^{d}(\omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma )(\omega _it^{-c})^{-d}$![]() and $\omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma$
and $\omega _i^{*}(t^{-2c}\sigma ^{-1}t^{2c})\sigma$![]() produces $t^{-4c(m+n+1)}(1\;2\;3)t^{4c(m+n+1)}$
produces $t^{-4c(m+n+1)}(1\;2\;3)t^{4c(m+n+1)}$![]() . We can assume that $\sigma \in \operatorname {Alt}(\mathbb {Z})$
. We can assume that $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() by potentially composing it with $(x\;x+1)$
by potentially composing it with $(x\;x+1)$![]() for some suitably large $x\in \mathbb {N}$
for some suitably large $x\in \mathbb {N}$![]() . Then, for every $i\in \{1,\, \ldots,\, n\}$
. Then, for every $i\in \{1,\, \ldots,\, n\}$![]() , we have that $\langle s_{\sigma }^{k},\, g_i\rangle \geqslant \langle s_{\sigma }^{k},\, \Lambda \rangle \geqslant \langle s_\sigma ^{k},\, \operatorname {Alt}(\mathbb {Z})\rangle =G_k$
, we have that $\langle s_{\sigma }^{k},\, g_i\rangle \geqslant \langle s_{\sigma }^{k},\, \Lambda \rangle \geqslant \langle s_\sigma ^{k},\, \operatorname {Alt}(\mathbb {Z})\rangle =G_k$![]() .
.
Remark 4.5 There is great flexibility for the element $\sigma$![]() in the above proof. First, given any $m'\in \mathbb {N}$
in the above proof. First, given any $m'\in \mathbb {N}$![]() , we can insist that $\operatorname {supp}(\sigma )\cap \{-m',\, \ldots,\, m'\}=\emptyset$
, we can insist that $\operatorname {supp}(\sigma )\cap \{-m',\, \ldots,\, m'\}=\emptyset$![]() . Secondly, given any $\tau \in \operatorname {Alt}(\mathbb {Z})$
. Secondly, given any $\tau \in \operatorname {Alt}(\mathbb {Z})$![]() , we can choose $m'$
, we can choose $m'$![]() large enough so that $\operatorname {supp}(\sigma )\cap \operatorname {supp}(\tau )=\emptyset$
large enough so that $\operatorname {supp}(\sigma )\cap \operatorname {supp}(\tau )=\emptyset$![]() and that $s_{\sigma \tau }^{k}$
and that $s_{\sigma \tau }^{k}$![]() and $s_{\tau \sigma }^{k}$
and $s_{\tau \sigma }^{k}$![]() both generate $G_k$
both generate $G_k$![]() with each of $g_1,\, \ldots,\, g_n\in G_k\setminus \operatorname {Alt}(\mathbb {Z})$
with each of $g_1,\, \ldots,\, g_n\in G_k\setminus \operatorname {Alt}(\mathbb {Z})$![]() .
.
The previous theorem reveals curious properties for the generating graphs of each group $G_k$![]() (which is a graph with vertex set $G$
(which is a graph with vertex set $G$![]() and an edge between vertices which generate the group). If we consider the elements of $G_k$
and an edge between vertices which generate the group). If we consider the elements of $G_k$![]() as obtained through the union of balls $B_n(G_k,\, X)$
as obtained through the union of balls $B_n(G_k,\, X)$![]() for some finite generating set $X$
for some finite generating set $X$![]() of $G_k$
of $G_k$![]() , then, by the previous lemma, for each $m\in \mathbb {N}$
, then, by the previous lemma, for each $m\in \mathbb {N}$![]() we can construct an element $\gamma _m\in \operatorname {Alt}(\mathbb {Z})$
we can construct an element $\gamma _m\in \operatorname {Alt}(\mathbb {Z})$![]() such that $\gamma _m^{-1}t^{k}\gamma _m$
such that $\gamma _m^{-1}t^{k}\gamma _m$![]() generates $G_k$
generates $G_k$![]() with every element in $B_m(G_k,\, S)\setminus \operatorname {Alt}(\mathbb {Z})$
with every element in $B_m(G_k,\, S)\setminus \operatorname {Alt}(\mathbb {Z})$![]() . Since $B_n(G_k,\, X)$
. Since $B_n(G_k,\, X)$![]() grows exponentially with $n$
grows exponentially with $n$![]() , the set $\{\gamma _m^{-1}t^{k}\gamma _m\;:\;m\in \mathbb {N}\}$
, the set $\{\gamma _m^{-1}t^{k}\gamma _m\;:\;m\in \mathbb {N}\}$![]() can be considered as ‘small’ in $G_k$
can be considered as ‘small’ in $G_k$![]() . Note also the similarity to what is known, from [Reference Burness and Harper8], for finite simple groups. In that world, there is a ‘small’ set of elements $S$
. Note also the similarity to what is known, from [Reference Burness and Harper8], for finite simple groups. In that world, there is a ‘small’ set of elements $S$![]() – in certain cases of size 2 – such that for every $g \in G\setminus \{1\}$
– in certain cases of size 2 – such that for every $g \in G\setminus \{1\}$![]() there exists an $s \in S$
there exists an $s \in S$![]() such that $\langle g,\, s\rangle =G$
such that $\langle g,\, s\rangle =G$![]() .
.
5. Conditions for the generation of $G_1$ and $G_2$
and $G_2$
We start with criteria for when a $3$![]() -cycle generates $G_1$
-cycle generates $G_1$![]() with the element $t$
with the element $t$![]() .
.
Lemma 5.1 Let $\omega \in \operatorname {Alt}(\mathbb {Z}),$![]() $s:=s_\omega,$
$s:=s_\omega,$![]() and $a,\, b\in \mathbb {Z}$
and $a,\, b\in \mathbb {Z}$![]() with $a<0< b$
with $a<0< b$![]() . Define $d_a,\, d_b\in \mathbb {N}$
. Define $d_a,\, d_b\in \mathbb {N}$![]() such that $(a)s^{d_a}=0$
such that $(a)s^{d_a}=0$![]() and $(b)s^{-d_b}=0$
and $(b)s^{-d_b}=0$![]() . Then $\langle (a\;0\;b),\, s\rangle =G_1$
. Then $\langle (a\;0\;b),\, s\rangle =G_1$![]() if and only if $\gcd (d_a,\, d_b)=1$
if and only if $\gcd (d_a,\, d_b)=1$![]() .
.
Proof. We change our perspective by relabelling $\mathbb {Z}$![]() so to replace $s$
so to replace $s$![]() with $t$
with $t$![]() and $(a\;0\;b)$
and $(a\;0\;b)$![]() with $(-d_a\;0\;d_b)$
with $(-d_a\;0\;d_b)$![]() . If $\gcd (d_a,\, d_b)=1$
. If $\gcd (d_a,\, d_b)=1$![]() , then apply the Euclidean algorithm to $(-d_a\;0\;d_b)$
, then apply the Euclidean algorithm to $(-d_a\;0\;d_b)$![]() using $t$
using $t$![]() to obtain $(-1\;0\;m)$
to obtain $(-1\;0\;m)$![]() or $(-m\;0\;1)$
or $(-m\;0\;1)$![]() for some $m \in \mathbb {N}$
for some $m \in \mathbb {N}$![]() , which both then reduce to $(-1\;0\;1)$
, which both then reduce to $(-1\;0\;1)$![]() .
.
On the other hand, if $\gcd (d_a,\, d_b)=k>1$![]() , then we claim that the set of torsion elements in $\langle (-d_a\;0\;d_b),\, t\rangle$
, then we claim that the set of torsion elements in $\langle (-d_a\;0\;d_b),\, t\rangle$![]() preserve a non-trivial block structure of $\mathbb {Z}$
preserve a non-trivial block structure of $\mathbb {Z}$![]() . We work with $\langle (-k\;0\;k),\, t\rangle$
. We work with $\langle (-k\;0\;k),\, t\rangle$![]() , since this contains $\langle (-d_a\;0\;d_b),\, t\rangle$
, since this contains $\langle (-d_a\;0\;d_b),\, t\rangle$![]() . A torsion element in $\langle (-k\;0\;k),\, t\rangle$
. A torsion element in $\langle (-k\;0\;k),\, t\rangle$![]() will be a product of $t$
will be a product of $t$![]() -conjugates of $(-k\;0\;k)$
-conjugates of $(-k\;0\;k)$![]() and $(-k\;0\;k)^{-1}$
and $(-k\;0\;k)^{-1}$![]() . Then both $(-k\;0\;k)$
. Then both $(-k\;0\;k)$![]() and $(-k\;0\;k)^{-1}$
and $(-k\;0\;k)^{-1}$![]() fix all but one of the sets
fix all but one of the sets
and every $t$![]() -conjugate of $(-k\;0\;k)^{\pm 1}$
-conjugate of $(-k\;0\;k)^{\pm 1}$![]() also has this property.
also has this property.
The following is a specific case of [Reference Cox10, Lem. 2.4].
Lemma 5.2 Let $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() . Then there exists an $\omega \in \operatorname {FSym}(\mathbb {Z})$
. Then there exists an $\omega \in \operatorname {FSym}(\mathbb {Z})$![]() such that $\langle s_\omega,\, \sigma \rangle =G_1$
such that $\langle s_\omega,\, \sigma \rangle =G_1$![]() . Moreover, given any $\tau \in \operatorname {FSym}(\mathbb {Z})$
. Moreover, given any $\tau \in \operatorname {FSym}(\mathbb {Z})$![]() with $\operatorname {supp}(\tau )$
with $\operatorname {supp}(\tau )$![]() disjoint from $\operatorname {supp}(\sigma )\cup \operatorname {supp}(\omega ),$
disjoint from $\operatorname {supp}(\sigma )\cup \operatorname {supp}(\omega ),$![]() we have that $\langle s_{\tau \omega },\, \sigma \rangle =\langle s_{\omega \tau },\, \sigma \rangle =G_1$
we have that $\langle s_{\tau \omega },\, \sigma \rangle =\langle s_{\omega \tau },\, \sigma \rangle =G_1$![]() .
.
Proof. As with the previous lemma, we start by reordering $\mathbb {Z}$![]() to consider $t$
to consider $t$![]() rather than $s_\omega$
rather than $s_\omega$![]() , at the cost of then working with $\sigma _*=\gamma ^{-1}\sigma \gamma$
, at the cost of then working with $\sigma _*=\gamma ^{-1}\sigma \gamma$![]() rather than $\sigma$
rather than $\sigma$![]() . With this perspective, the claims regarding $\tau$
. With this perspective, the claims regarding $\tau$![]() follow immediately.
follow immediately.
Let $\sigma _*=\sigma _1\ldots \sigma _n$![]() be written in disjoint cycle notation and let $\max \{\operatorname {supp}(\sigma _*)\}=\max \{\operatorname {supp}(\sigma _n)\}=y$
be written in disjoint cycle notation and let $\max \{\operatorname {supp}(\sigma _*)\}=\max \{\operatorname {supp}(\sigma _n)\}=y$![]() . We can choose $\gamma$
. We can choose $\gamma$![]() so that $(y)\sigma _*^{-1}=y-1$
so that $(y)\sigma _*^{-1}=y-1$![]() .
.
Conjugate $\sigma _*$![]() by a power of $t$
by a power of $t$![]() to obtain $\alpha$
to obtain $\alpha$![]() where $\min \{\operatorname {supp}(\alpha )\}=y$
where $\min \{\operatorname {supp}(\alpha )\}=y$![]() . We can then conjugate $\sigma _*$
. We can then conjugate $\sigma _*$![]() by $\alpha$
by $\alpha$![]() to obtain $\sigma '$
to obtain $\sigma '$![]() where, by construction, $(x)\sigma _*=(x)\sigma '$
where, by construction, $(x)\sigma _*=(x)\sigma '$![]() for all $x< y$
for all $x< y$![]() .
.
We will now consider the element $\sigma _*(\sigma ')^{-1}$![]() . Recall that $\sigma _*=\sigma _1\ldots \sigma _n$
. Recall that $\sigma _*=\sigma _1\ldots \sigma _n$![]() , and, from our construction, $\sigma '=\sigma _1\ldots \sigma _{n-1}\sigma _n'$
, and, from our construction, $\sigma '=\sigma _1\ldots \sigma _{n-1}\sigma _n'$![]() where
where
Therefore $\sigma _*(\sigma ')^{-1}=\sigma _n(\sigma '_n)^{-1}=(x_{r_n-1}^{(n)}\;x_{r_n}^{(n)}\;m)=(y-1\;y\;m)$![]() , which then, together with $t$
, which then, together with $t$![]() , generates $G_1$
, generates $G_1$![]() by Lemma 5.1.
by Lemma 5.1.
Lemma 5.3 For any $z\in \mathbb {Z},$![]() we have that $\langle (2z-1\;0\;2),\, t^{2}\rangle =\langle (2z\;1\;3),\, t^{2}\rangle =G_2$
we have that $\langle (2z-1\;0\;2),\, t^{2}\rangle =\langle (2z\;1\;3),\, t^{2}\rangle =G_2$![]() .
.
Proof. Starting with an arbitrary odd $d\in \mathbb {Z}$![]() , if we conjugate $(d\;0\;2)$
, if we conjugate $(d\;0\;2)$![]() by $t^{-2}(d\;0\;2)t^{2}$
by $t^{-2}(d\;0\;2)t^{2}$![]() then we obtain $(d\;0\;4)$
then we obtain $(d\;0\;4)$![]() . Then $(d\;0\;2)(d\;4\;0)=(0\;2\;4)$
. Then $(d\;0\;2)(d\;4\;0)=(0\;2\;4)$![]() which conjugates $(d\;0\;2)$
which conjugates $(d\;0\;2)$![]() to $(d\;2\;4)$
to $(d\;2\;4)$![]() . Now $t^{2}(d\;2\;4)t^{-2}=(e\;0\;2)$
. Now $t^{2}(d\;2\;4)t^{-2}=(e\;0\;2)$![]() where $e=d-2$
where $e=d-2$![]() , and hence $\langle (d\;0\;2),\, t^{2}\rangle$
, and hence $\langle (d\;0\;2),\, t^{2}\rangle$![]() contains $(1\;0\;2)$
contains $(1\;0\;2)$![]() and so $\operatorname {Alt}(\mathbb {Z})$
and so $\operatorname {Alt}(\mathbb {Z})$![]() . For the other case, we note that $tG_2t^{-1}=G_2$
. For the other case, we note that $tG_2t^{-1}=G_2$![]() .
.
The preceding lemma allows us to generalize the argument of Lemma 5.2 to $G_2$![]() .
.
Lemma 5.4 Let $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() . Then there exists an $\omega \in \operatorname {FSym}(\mathbb {Z})$
. Then there exists an $\omega \in \operatorname {FSym}(\mathbb {Z})$![]() such that $\langle s_\omega ^{2},\, \sigma \rangle =G_2$
such that $\langle s_\omega ^{2},\, \sigma \rangle =G_2$![]() . Moreover, given any $\tau \in \operatorname {FSym}(\mathbb {Z})$
. Moreover, given any $\tau \in \operatorname {FSym}(\mathbb {Z})$![]() with $\operatorname {supp}(\tau )$
with $\operatorname {supp}(\tau )$![]() disjoint from $\operatorname {supp}(\sigma )\cup \operatorname {supp}(\omega ),$
disjoint from $\operatorname {supp}(\sigma )\cup \operatorname {supp}(\omega ),$![]() we have that $\langle s_{\tau \omega }^{2},\, \sigma \rangle =\langle s_{\omega \tau }^{2},\, \sigma \rangle =G_2$
we have that $\langle s_{\tau \omega }^{2},\, \sigma \rangle =\langle s_{\omega \tau }^{2},\, \sigma \rangle =G_2$![]() .
.
Proof. As with the proof of Lemma 5.2, we change our perspective and so work with $t^{2}$![]() rather than $s_\omega ^{2}$
rather than $s_\omega ^{2}$![]() , at the cost of then working with $\sigma _*=\gamma ^{-1}\sigma \gamma$
, at the cost of then working with $\sigma _*=\gamma ^{-1}\sigma \gamma$![]() rather than $\sigma$
rather than $\sigma$![]() . This again resolves the claims regarding $\tau$
. This again resolves the claims regarding $\tau$![]() .
.
If $\sigma$![]() is a $3$
is a $3$![]() -cycle, then we choose $\gamma$
-cycle, then we choose $\gamma$![]() so that $\operatorname {supp}(\sigma _*)=\{0,\, 1,\, 2\}$
so that $\operatorname {supp}(\sigma _*)=\{0,\, 1,\, 2\}$![]() . Otherwise we recall the notation from Lemma 5.2, and write $\sigma _*=\sigma _1\ldots \sigma _n$
. Otherwise we recall the notation from Lemma 5.2, and write $\sigma _*=\sigma _1\ldots \sigma _n$![]() where
where
and choose $\gamma \in \operatorname {Alt}(\mathbb {Z})$![]() so that:
so that:
• $x_{r_n}^{(n)}$
 is even and maximal in $\operatorname {supp}(\sigma _*)$
is even and maximal in $\operatorname {supp}(\sigma _*)$ ;
;• $x_{r_n-1}^{(n)}$
 is odd;
is odd;• $x_1^{(1)}=0$
 and is minimal in $\operatorname {supp}(\sigma _*)$
and is minimal in $\operatorname {supp}(\sigma _*)$ ; and
; and• $x_2^{(1)}=2$
 .
.
Now conjugate $\sigma _*$![]() by a suitable power of $t^{2}$
by a suitable power of $t^{2}$![]() to produce an element $\alpha \in \operatorname {Alt}(\mathbb {Z})$
to produce an element $\alpha \in \operatorname {Alt}(\mathbb {Z})$![]() with $\min \{\operatorname {supp}(\alpha )\}=x_{r_n}^{(n)}$
with $\min \{\operatorname {supp}(\alpha )\}=x_{r_n}^{(n)}$![]() and conjugate $\sigma _*$
and conjugate $\sigma _*$![]() by $\alpha$
by $\alpha$![]() to obtain $\sigma '$
to obtain $\sigma '$![]() . With this construction $\sigma _*(\sigma ')^{-1}=(x_{r_n-1}^{(n)}\;x_{r_n}^{(n)}\;x_{r_n}^{(n)}+2)$
. With this construction $\sigma _*(\sigma ')^{-1}=(x_{r_n-1}^{(n)}\;x_{r_n}^{(n)}\;x_{r_n}^{(n)}+2)$![]() . Then $\langle \sigma _*(\sigma ')^{-1},\, t^{2}\rangle =G_2$
. Then $\langle \sigma _*(\sigma ')^{-1},\, t^{2}\rangle =G_2$![]() by Lemma 5.3.
by Lemma 5.3.
A group $G$![]() has a dominating set $S$
has a dominating set $S$![]() if for each $g\in G\setminus \{1\}$
if for each $g\in G\setminus \{1\}$![]() there exists an $s\in S$
there exists an $s\in S$![]() such that $\langle g,\, s\rangle =G$
such that $\langle g,\, s\rangle =G$![]() . A natural question is whether $G_1$
. A natural question is whether $G_1$![]() or $G_2$
or $G_2$![]() has a finite dominating set. Despite the strong result of Theorem 4.4, we find that the groups $G_k$
has a finite dominating set. Despite the strong result of Theorem 4.4, we find that the groups $G_k$![]() do not resolve the question of whether there is an infinite group – other than $\mathbb {Z}$
do not resolve the question of whether there is an infinite group – other than $\mathbb {Z}$![]() or the Tarski monsters – with a finite total dominating set.
or the Tarski monsters – with a finite total dominating set.
Proposition 5.5 No finite total dominating set exists for $G_1$![]() or $G_2$
or $G_2$![]() .
.
Proof. Consider the elements in $L=\{(k\;k+2\;k+4)\;:\;k\in \mathbb {N}\}$![]() . Given any finite sets $S_1\subset G_1$
. Given any finite sets $S_1\subset G_1$![]() and $S_2\subset G_2$
and $S_2\subset G_2$![]() , first produce $S_1^{*}$
, first produce $S_1^{*}$![]() and $S_2^{*}$
and $S_2^{*}$![]() such that $S_i^{*}$
such that $S_i^{*}$![]() contains elements with exactly $i$
contains elements with exactly $i$![]() infinite orbits. We do this because no element in $S_i\setminus S_i^{*}$
infinite orbits. We do this because no element in $S_i\setminus S_i^{*}$![]() can generate $G_i$
can generate $G_i$![]() with any element in $L$
with any element in $L$![]() .
.
Recall, by Remark 2.4, that there exists an $m\in \mathbb {N}$![]() such that each $g\in S_1^{*}\cup S_2^{*}$
such that each $g\in S_1^{*}\cup S_2^{*}$![]() translates all points $z>m$
translates all points $z>m$![]() . Now $(m\;m+2\;m+4)$
. Now $(m\;m+2\;m+4)$![]() cannot generate $G_1$
cannot generate $G_1$![]() with any $s \in S_1^{*}$
with any $s \in S_1^{*}$![]() by Lemma 5.1, and $(m\;m+2\;m+4)$
by Lemma 5.1, and $(m\;m+2\;m+4)$![]() cannot generate $G_2$
cannot generate $G_2$![]() with any $s'\in S_2^{*}$
with any $s'\in S_2^{*}$![]() since $m$
since $m$![]() , $m+2$
, $m+2$![]() , and $m+4$
, and $m+4$![]() all lie on the same orbit of each $s'\in S_2^{*}$
all lie on the same orbit of each $s'\in S_2^{*}$![]() .
.
6. Bounds on the spread and uniform spread of $G_1$ and $G_2$
and $G_2$
Our aim in this final section is to prove the following.
Theorem 6.1 Let $G_1=\langle (1\;2\;3),\, t\rangle$![]() and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$
and $G_2=\langle (1\;2\;3),\, t^{2}\rangle$![]() . Then $u(G_1)\geqslant 2,$
. Then $u(G_1)\geqslant 2,$![]() $u(G_2)\geqslant 2,$
$u(G_2)\geqslant 2,$![]() $s(G_1)\leqslant 9,$
$s(G_1)\leqslant 9,$![]() and $s(G_2)\leqslant 9$
and $s(G_2)\leqslant 9$![]() .
.
Our proof naturally breaks into four parts. To show that $u(G_1)\geqslant 2$![]() , we show that given any $g_1,\, g_2 \in G_1$
, we show that given any $g_1,\, g_2 \in G_1$![]() there exists $s\in [t]$
there exists $s\in [t]$![]() which generates $G_1$
which generates $G_1$![]() with each of $g_1$
with each of $g_1$![]() and $g_2$
and $g_2$![]() . In a similar way, but using $[t^{2}]$
. In a similar way, but using $[t^{2}]$![]() rather than $[t]$
rather than $[t]$![]() , we show that $u(G_2)\geqslant 2$
, we show that $u(G_2)\geqslant 2$![]() . The upper bounds for $s(G_1)$
. The upper bounds for $s(G_1)$![]() and $s(G_2)$
and $s(G_2)$![]() are found in order to illustrate that these groups have finite spread, and so are unlikely to be optimal.
are found in order to illustrate that these groups have finite spread, and so are unlikely to be optimal.
Notation Given $g,\, h \in G$![]() , let $g^{h}:=h^{-1}gh$
, let $g^{h}:=h^{-1}gh$![]() .
.
Lemma 6.2 Let $g_1,\, g_2\in \operatorname {Alt}(\mathbb {Z})$![]() . Then there exists an $h\in [t]\subset G_1$
. Then there exists an $h\in [t]\subset G_1$![]() such that $\langle h,\, g_1\rangle =\langle h,\, g_2\rangle =G_1$
such that $\langle h,\, g_1\rangle =\langle h,\, g_2\rangle =G_1$![]() .
.
Proof. By reordering $\mathbb {Z}$![]() , we can work with $t$
, we can work with $t$![]() rather than $h$
rather than $h$![]() and aim to find an $\omega \in \operatorname {Alt}(\mathbb {Z})$
and aim to find an $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() such that $\langle g_1^{\omega },\, t\rangle =\langle g_2^{\omega },\, t\rangle =G_1$
such that $\langle g_1^{\omega },\, t\rangle =\langle g_2^{\omega },\, t\rangle =G_1$![]() .
.
First assume that $\operatorname {supp}(g_1)=\operatorname {supp}(g_2)$![]() . If $|\operatorname {supp}(g_1)|=3$
. If $|\operatorname {supp}(g_1)|=3$![]() , then $g_1\in \{g_2,\, g_2^{-1}\}$
, then $g_1\in \{g_2,\, g_2^{-1}\}$![]() and so we are done. Otherwise, let $y=\max \{\operatorname {supp}(g_1)\}$
and so we are done. Otherwise, let $y=\max \{\operatorname {supp}(g_1)\}$![]() , and define $x_1:=(y)g_1^{-1}$
, and define $x_1:=(y)g_1^{-1}$![]() , $x_2:=(y)g_2^{-1}$
, $x_2:=(y)g_2^{-1}$![]() , and fix some $a\in \operatorname {supp}(g_1)\setminus \{x_1,\, x_2,\, y\}$
, and fix some $a\in \operatorname {supp}(g_1)\setminus \{x_1,\, x_2,\, y\}$![]() . Choose $\omega \in \operatorname {Alt}(\mathbb {Z})$
. Choose $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() so that:
so that:
• $(y)\omega =:y'$
 is still maximal in $\operatorname {supp}(g_1^{\omega })$
is still maximal in $\operatorname {supp}(g_1^{\omega })$ ;
;• $a$
 is minimal in $\operatorname {supp}(g_1^{\omega })$
is minimal in $\operatorname {supp}(g_1^{\omega })$ ; and
; and• $(x_1)\omega =y'-1$
 .
.
Applying the steps in the proof of Lemma 5.2 to $g_1^{\omega }$![]() then yields $(y'-1\;y'\;m)$
then yields $(y'-1\;y'\;m)$![]() for some $m>y'$
for some $m>y'$![]() , and so Lemma 5.1 implies that $\langle g_1^{\omega },\, t\rangle =G_1$
, and so Lemma 5.1 implies that $\langle g_1^{\omega },\, t\rangle =G_1$![]() . We note that there is also some $d\in \mathbb {N}$
. We note that there is also some $d\in \mathbb {N}$![]() such that $(y')t^{-d}=(x_2)\omega$
such that $(y')t^{-d}=(x_2)\omega$![]() . Given $b_2:=(a)g_2^{\omega }$
. Given $b_2:=(a)g_2^{\omega }$![]() , we can therefore adjust $\omega$
, we can therefore adjust $\omega$![]() so that it moves $a$
so that it moves $a$![]() arbitrarily far away from the other points in $\operatorname {supp}(g_1^{\omega })$
arbitrarily far away from the other points in $\operatorname {supp}(g_1^{\omega })$![]() , i.e. we can assume that $(a)t^{p}=b_2$
, i.e. we can assume that $(a)t^{p}=b_2$![]() , where $p$
, where $p$![]() is a suitably large prime number so that $\gcd (d,\, p)=1$
is a suitably large prime number so that $\gcd (d,\, p)=1$![]() . Again, applying the steps from the proof of Lemma 5.2 will yield $(y'-d\;y'\;y'+p)$
. Again, applying the steps from the proof of Lemma 5.2 will yield $(y'-d\;y'\;y'+p)$![]() and so $\langle g_2^{\omega },\, t\rangle \geqslant \langle (-d\;0\;p),\, t\rangle =G_1$
and so $\langle g_2^{\omega },\, t\rangle \geqslant \langle (-d\;0\;p),\, t\rangle =G_1$![]() by Lemma 5.1.
by Lemma 5.1.
If $\operatorname {supp}(g_1)\ne \operatorname {supp}(g_2)$![]() then, without loss of generality, $\operatorname {supp}(g_1)\setminus \operatorname {supp}(g_2)\ne \emptyset$
then, without loss of generality, $\operatorname {supp}(g_1)\setminus \operatorname {supp}(g_2)\ne \emptyset$![]() and we can fix some $\alpha$
and we can fix some $\alpha$![]() in this set. Imagine that $\{\alpha g_1^{k}\;:\;k\in \mathbb {N}\}\cap \operatorname {supp}(g_2)=\emptyset$
in this set. Imagine that $\{\alpha g_1^{k}\;:\;k\in \mathbb {N}\}\cap \operatorname {supp}(g_2)=\emptyset$![]() . By choosing $\omega \in \operatorname {FSym}(\mathbb {Z})$
. By choosing $\omega \in \operatorname {FSym}(\mathbb {Z})$![]() such that $(\alpha )g_1^{\omega }=\alpha +1$
such that $(\alpha )g_1^{\omega }=\alpha +1$![]() and $\alpha =\min (\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega }))$
and $\alpha =\min (\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega }))$![]() , we have that $\langle t,\, g_1^{\omega }\rangle =G_1$
, we have that $\langle t,\, g_1^{\omega }\rangle =G_1$![]() . Thus, choose $\omega$
. Thus, choose $\omega$![]() so that some point $y$
so that some point $y$![]() in $\operatorname {supp}(g_2^{\omega })$
in $\operatorname {supp}(g_2^{\omega })$![]() is maximal in $\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega })$
is maximal in $\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega })$![]() , and set $(y)(g_2^{\omega })^{-1}=y-1$
, and set $(y)(g_2^{\omega })^{-1}=y-1$![]() .
.
Now let $\alpha \in \operatorname {supp}(g_1)\setminus \operatorname {supp}(g_2)$![]() but assume that $(\alpha )g_1^{\omega }=\beta \in \operatorname {supp}(g_2^{\omega })$
but assume that $(\alpha )g_1^{\omega }=\beta \in \operatorname {supp}(g_2^{\omega })$![]() where $\alpha$
where $\alpha$![]() is minimal in $\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega })$
is minimal in $\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega })$![]() and $\beta =\alpha +1$
and $\beta =\alpha +1$![]() . Thus, $\langle t,\, g_1^{\omega }\rangle =G_1$
. Thus, $\langle t,\, g_1^{\omega }\rangle =G_1$![]() but also, by construction, $\beta$
but also, by construction, $\beta$![]() is minimal in $\operatorname {supp}(g_2^{\omega })$
is minimal in $\operatorname {supp}(g_2^{\omega })$![]() . We can therefore choose $\omega$
. We can therefore choose $\omega$![]() so that $(\beta )g_2^{\omega }=\beta +1$
so that $(\beta )g_2^{\omega }=\beta +1$![]() , so that $\langle t,\, g_2^{\omega }\rangle =G_1$
, so that $\langle t,\, g_2^{\omega }\rangle =G_1$![]() .
.
Lemma 6.3 The group $G_1$![]() has a uniform spread at least 2.
has a uniform spread at least 2.
Proof. Let $g_1,\, g_2 \in G_1$![]() . We will show that there exists $\alpha \in \operatorname {FSym}(\mathbb {Z})$
. We will show that there exists $\alpha \in \operatorname {FSym}(\mathbb {Z})$![]() such that $\langle s_\alpha,\, g_1\rangle = \langle s_\alpha,\, g_2\rangle =G_1$
such that $\langle s_\alpha,\, g_1\rangle = \langle s_\alpha,\, g_2\rangle =G_1$![]() . The case where $g_1,\, g_2 \in \operatorname {Alt}(\mathbb {Z})$
. The case where $g_1,\, g_2 \in \operatorname {Alt}(\mathbb {Z})$![]() is dealt with in the previous lemma. If $g_1,\, g_2 \in G_1\setminus \operatorname {Alt}(\mathbb {Z})$
is dealt with in the previous lemma. If $g_1,\, g_2 \in G_1\setminus \operatorname {Alt}(\mathbb {Z})$![]() , then Theorem 4.4 implies the result. Finally, if $g_1 \in \operatorname {Alt}(\mathbb {Z})$
, then Theorem 4.4 implies the result. Finally, if $g_1 \in \operatorname {Alt}(\mathbb {Z})$![]() and $g_2\in G_1\setminus \operatorname {Alt}(\mathbb {Z})$
and $g_2\in G_1\setminus \operatorname {Alt}(\mathbb {Z})$![]() , then we can apply Lemma 5.2 so to find $s_\omega$
, then we can apply Lemma 5.2 so to find $s_\omega$![]() which generates $G_1$
which generates $G_1$![]() with $g_1$
with $g_1$![]() . This lemma also states that choosing any $\tau \in \operatorname {FSym}(\mathbb {Z})$
. This lemma also states that choosing any $\tau \in \operatorname {FSym}(\mathbb {Z})$![]() such that $\operatorname {supp}(\tau )$
such that $\operatorname {supp}(\tau )$![]() is disjoint from $\operatorname {supp}(\omega )\cup \operatorname {supp}(g_1)$
is disjoint from $\operatorname {supp}(\omega )\cup \operatorname {supp}(g_1)$![]() will result in $\langle s_{\tau \omega },\, g_1\rangle =G_1$
will result in $\langle s_{\tau \omega },\, g_1\rangle =G_1$![]() . Theorem 4.4 and Remark 4.5 together ensure the existence of an element $\alpha =\sigma \omega \in \operatorname {Alt}(\mathbb {Z})$
. Theorem 4.4 and Remark 4.5 together ensure the existence of an element $\alpha =\sigma \omega \in \operatorname {Alt}(\mathbb {Z})$![]() so that $\langle g_1,\, s_\alpha \rangle =\langle g_2,\, s_\alpha \rangle =G_1$
so that $\langle g_1,\, s_\alpha \rangle =\langle g_2,\, s_\alpha \rangle =G_1$![]() .
.
We now show that $s(G_2)\geqslant 2$![]() . As we did for $G_1$
. As we did for $G_1$![]() , we deal separately with the case where the given elements are both in $\operatorname {Alt}(\mathbb {Z})$
, we deal separately with the case where the given elements are both in $\operatorname {Alt}(\mathbb {Z})$![]() . We do approach $G_2$
. We do approach $G_2$![]() differently however, since the methods we used for $G_1$
differently however, since the methods we used for $G_1$![]() appear to be too weak. This is because the conditions for a $3$
appear to be too weak. This is because the conditions for a $3$![]() -cycle to generate $G_2$
-cycle to generate $G_2$![]() with $t^{2}$
with $t^{2}$![]() are more restrictive than the conditions for a $3$
are more restrictive than the conditions for a $3$![]() -cycle to generate $G_1$
-cycle to generate $G_1$![]() with $t$
with $t$![]() . Our approach takes some inspiration from [Reference Brenner and Wiegold2, Cor. 3.04], by partitioning $\mathbb {Z}$
. Our approach takes some inspiration from [Reference Brenner and Wiegold2, Cor. 3.04], by partitioning $\mathbb {Z}$![]() into two parts and working separately with each. We partition $\mathbb {Z}$
into two parts and working separately with each. We partition $\mathbb {Z}$![]() into even and odd numbers, which we use because these are the two orbits of $t^{2}$
into even and odd numbers, which we use because these are the two orbits of $t^{2}$![]() .
.
Notation Let $2\mathbb {Z}$![]() and $2\mathbb {Z}+1$
and $2\mathbb {Z}+1$![]() denote the sets of even and odd integers, respectively.
denote the sets of even and odd integers, respectively.
Our first step is to show that we can focus on generating $\operatorname {Alt}(2\mathbb {Z}+1)$![]() rather than $\operatorname {Alt}(\mathbb {Z})$
rather than $\operatorname {Alt}(\mathbb {Z})$![]() . We will then use this simplification in order to show that $u(G_2)\geqslant 2$
. We will then use this simplification in order to show that $u(G_2)\geqslant 2$![]() .
.
Lemma 6.4 If $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() has an orbit containing both an even and an odd integer, then $\langle \sigma,\, \operatorname {Alt}(2\mathbb {Z}+1),\, t^{2}\rangle =G_2$
has an orbit containing both an even and an odd integer, then $\langle \sigma,\, \operatorname {Alt}(2\mathbb {Z}+1),\, t^{2}\rangle =G_2$![]() .
.
Proof. First, conjugate $\sigma$![]() by a suitable power of $t^{2}$
by a suitable power of $t^{2}$![]() to produce $\sigma _*$
to produce $\sigma _*$![]() , where $\sigma _*$
, where $\sigma _*$![]() sends $0$
sends $0$![]() to a point in $2\mathbb {Z}+1$
to a point in $2\mathbb {Z}+1$![]() and $\sigma _*$
and $\sigma _*$![]() sends no negative even number to $2\mathbb {Z}+1$
sends no negative even number to $2\mathbb {Z}+1$![]() . Now, given $\omega \in \operatorname {Alt}(\mathbb {Z})$
. Now, given $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() with $|\operatorname {supp}(\omega )\cap 2\mathbb {Z}|=k>0$
with $|\operatorname {supp}(\omega )\cap 2\mathbb {Z}|=k>0$![]() , we consider the following steps:
, we consider the following steps:
i. conjugate $\omega$
 by a suitable power of $t^{2}$
by a suitable power of $t^{2}$ to produce $\omega '$
to produce $\omega '$ so that $0\in \operatorname {supp}(\omega ')$
so that $0\in \operatorname {supp}(\omega ')$ and $\operatorname {supp}(\omega ')\cap 2\mathbb {N}=\emptyset$
and $\operatorname {supp}(\omega ')\cap 2\mathbb {N}=\emptyset$ ;
;ii. conjugate $\omega '$
 by an appropriate element of $\operatorname {Alt}(2\mathbb {Z}+1)$
by an appropriate element of $\operatorname {Alt}(2\mathbb {Z}+1)$ to produce $\omega _*$
to produce $\omega _*$ with $\operatorname {supp}(\sigma _*)\cap \operatorname {supp}(\omega _*)\subset 2\mathbb {Z}$
with $\operatorname {supp}(\sigma _*)\cap \operatorname {supp}(\omega _*)\subset 2\mathbb {Z}$ ;
;iii. conjugate $\omega _*$
 by $\sigma _*$
by $\sigma _*$ to produce $\hat {\omega }$
to produce $\hat {\omega }$ .
.
Note that $|\operatorname {supp}(\hat {\omega })\cap 2\mathbb {Z}|=|\operatorname {supp}(\omega )\cap 2\mathbb {Z}|-1$![]() . Iterating these steps, therefore, results in an element in $\operatorname {Alt}(2\mathbb {Z}+1)$
. Iterating these steps, therefore, results in an element in $\operatorname {Alt}(2\mathbb {Z}+1)$![]() .
.
Proposition 6.5 Given any $g_1,\, g_2\in \operatorname {Alt}(\mathbb {Z}),$![]() there exists $s\in [t^{2}]$
there exists $s\in [t^{2}]$![]() which generates $G_2$
which generates $G_2$![]() with both $g_1$
with both $g_1$![]() and $g_2$
and $g_2$![]() .
.
Proof. Again, by relabelling $\mathbb {Z}$![]() , we deal with the equivalent problem of whether there exists $\omega \in \operatorname {Alt}(\mathbb {Z})$
, we deal with the equivalent problem of whether there exists $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() such that $\langle g_1^{\omega },\, t^{2}\rangle =\langle g_2^{\omega },\, t^{2}\rangle =G_2$
such that $\langle g_1^{\omega },\, t^{2}\rangle =\langle g_2^{\omega },\, t^{2}\rangle =G_2$![]() . If $\operatorname {supp}(g_1)\cap \operatorname {supp}(g_2)=\emptyset$
. If $\operatorname {supp}(g_1)\cap \operatorname {supp}(g_2)=\emptyset$![]() , then Lemma 5.4 implies the result. Otherwise, fix some $c\in \operatorname {supp}(g_1)\cap \operatorname {supp}(g_2)$
, then Lemma 5.4 implies the result. Otherwise, fix some $c\in \operatorname {supp}(g_1)\cap \operatorname {supp}(g_2)$![]() . We will restrict ourselves to those $\omega \in \operatorname {Alt}(\mathbb {Z})$
. We will restrict ourselves to those $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() such that:
such that:
• $(c)\omega =0$
 ;
;• $(\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega }))\cap 2\mathbb {Z}=\{0\}$
 ; and
; and• the only positive odd integers in $\operatorname {supp}(g_1^{\omega })\cup \operatorname {supp}(g_2^{\omega })$
 are $1$
are $1$ and $3$
and $3$ .
.
In light of the previous lemma, our aim is to choose $\omega$![]() so to relabel the points in $\operatorname {supp}(g_1)\cup \operatorname {supp}(g_2)$
so to relabel the points in $\operatorname {supp}(g_1)\cup \operatorname {supp}(g_2)$![]() so that both $\langle g_1^{\omega },\, t^{2}\rangle$
so that both $\langle g_1^{\omega },\, t^{2}\rangle$![]() and $\langle g_1^{\omega },\, t^{2}\rangle$
and $\langle g_1^{\omega },\, t^{2}\rangle$![]() contain $\operatorname {Alt}(2\mathbb {Z}+1)$
contain $\operatorname {Alt}(2\mathbb {Z}+1)$![]() .
.
Note that $|\operatorname {supp}(g_1)|\geqslant 3$![]() . Hence there exist distinct $x,\, y$
. Hence there exist distinct $x,\, y$![]() , both not equal to $c$
, both not equal to $c$![]() , with $(x)g_1=y$
, with $(x)g_1=y$![]() . We now further restrict our choice of $\omega$
. We now further restrict our choice of $\omega$![]() to those such that:
to those such that:
• $(x)\omega =1$
 ; and
; and• $(y)\omega =3$
 .
.
To simplify the cases we consider later, we impose that if $y\in \operatorname {supp}(g_2)$![]() , then so is $x$
, then so is $x$![]() . This is not a problematic choice: if only $y$
. This is not a problematic choice: if only $y$![]() were in $\operatorname {supp}(g_2)$
were in $\operatorname {supp}(g_2)$![]() , then we could replace $g_1$
, then we could replace $g_1$![]() with $g_1^{-1}$
with $g_1^{-1}$![]() and then swap the labels for $x$
and then swap the labels for $x$![]() and $y$
and $y$![]() . We first note that any choice of $\omega \in \operatorname {Alt}(\mathbb {Z})$
. We first note that any choice of $\omega \in \operatorname {Alt}(\mathbb {Z})$![]() with the above properties gives $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_1^{\omega },\, t^{2}\rangle$
with the above properties gives $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_1^{\omega },\, t^{2}\rangle$![]() . We prove this in two parts. If $|\operatorname {supp}(g_1)|=3$
. We prove this in two parts. If $|\operatorname {supp}(g_1)|=3$![]() , then we apply Lemma 5.3 to obtain that $\langle g_1^{\omega },\, t^{2}\rangle =G_2$
, then we apply Lemma 5.3 to obtain that $\langle g_1^{\omega },\, t^{2}\rangle =G_2$![]() . Otherwise, we apply the following steps, which we have employed numerous times in this paper so far (the first time being in Lemma 5.2).
. Otherwise, we apply the following steps, which we have employed numerous times in this paper so far (the first time being in Lemma 5.2).
1. Let $a:=\min (\operatorname {supp}(g_1^{\omega })\setminus \{0,\, 1,\, 3\})$
 . From our restrictions on $\omega$
. From our restrictions on $\omega$ , $a$
, $a$ is odd.
is odd.2. Conjugate $g_1^{\omega }$
 by a power of $t^{2}$
by a power of $t^{2}$ to obtain $\alpha$
to obtain $\alpha$ , an element with $\min (\operatorname {supp}(\alpha ))=3$
, an element with $\min (\operatorname {supp}(\alpha ))=3$ .
.3. Conjugate $g_1^{\omega }$
 by $\alpha$
by $\alpha$ to obtain $g_1'$
to obtain $g_1'$ . Note, for every $z \in \mathbb {Z}\setminus \{1,\, 3,\, (3)g_1^{\omega }\}$
. Note, for every $z \in \mathbb {Z}\setminus \{1,\, 3,\, (3)g_1^{\omega }\}$ , that $(z)g_1^{\omega }=(z)g_1'$
, that $(z)g_1^{\omega }=(z)g_1'$ .
.4. Let $g_1^{*}:=g_1^{\omega } (g_1')^{-1}$
 . Then $g_1^{*}=(1\;3\;m)$
. Then $g_1^{*}=(1\;3\;m)$ , where $m=(3)\alpha$
, where $m=(3)\alpha$ .
.
This element $g_1^{*}$![]() is exactly what we need. If $(3)\alpha \in 2\mathbb {Z}$
is exactly what we need. If $(3)\alpha \in 2\mathbb {Z}$![]() then $\langle g_1^{*},\, t^{2}\rangle =G_2$
then $\langle g_1^{*},\, t^{2}\rangle =G_2$![]() by Lemma 5.3. If $(3)\alpha \in 2\mathbb {Z}+1$
by Lemma 5.3. If $(3)\alpha \in 2\mathbb {Z}+1$![]() then, by focusing on the action of $t^{2}$
then, by focusing on the action of $t^{2}$![]() and $(1\;3\;m)$
and $(1\;3\;m)$![]() on $2\mathbb {Z}+1$
on $2\mathbb {Z}+1$![]() , we can apply Lemma 5.1 to see that $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_1^{*},\, t^{2}\rangle$
, we can apply Lemma 5.1 to see that $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_1^{*},\, t^{2}\rangle$![]() .
.
We must now choose the image of $\omega$![]() on $\operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$
on $\operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$![]() so to guarantee that $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_2^{\omega },\, t^{2}\rangle$
so to guarantee that $\operatorname {Alt}(2\mathbb {Z}+1)\leqslant \langle g_2^{\omega },\, t^{2}\rangle$![]() . First, if $1$
. First, if $1$![]() and $3$
and $3$![]() lie on the same orbit of $g_2^{\omega }$
lie on the same orbit of $g_2^{\omega }$![]() , then there exists $f_2$
, then there exists $f_2$![]() , a suitable power of $g_2^{\omega }$
, a suitable power of $g_2^{\omega }$![]() , such that $(1)f_2=3$
, such that $(1)f_2=3$![]() . The steps given above then imply that $\langle f_2,\, t^{2}\rangle =G_2$
. The steps given above then imply that $\langle f_2,\, t^{2}\rangle =G_2$![]() for any choice of $\omega$
for any choice of $\omega$![]() with the properties we have specified above. Similarly, if there exist $a,\, b\in \operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$
with the properties we have specified above. Similarly, if there exist $a,\, b\in \operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$![]() which lie on the same orbit of $g_2$
which lie on the same orbit of $g_2$![]() , then we can produce $h_2$
, then we can produce $h_2$![]() , a suitable power of $g_2$
, a suitable power of $g_2$![]() such that $(a)h_2=b$
such that $(a)h_2=b$![]() . We can insist that $\omega$
. We can insist that $\omega$![]() preserves the ordering on $\operatorname {supp}(h_2)\setminus \{c,\, x,\, y,\, a,\, b\}$
preserves the ordering on $\operatorname {supp}(h_2)\setminus \{c,\, x,\, y,\, a,\, b\}$![]() , and let $q:=\max (\operatorname {supp}(h_2))$
, and let $q:=\max (\operatorname {supp}(h_2))$![]() . By choosing $\omega$
. By choosing $\omega$![]() so that:
so that:
• $a$
 is odd;
is odd;• $a$
 is minimal in $\operatorname {supp}(g_2^{\omega })$
is minimal in $\operatorname {supp}(g_2^{\omega })$ ; and
; and• $b=a+2$

we see that the steps (1)–(4) above yield the $3$![]() -cycle $((1)h_2^{-1}\;q\;q+2)$
-cycle $((1)h_2^{-1}\;q\;q+2)$![]() . As we saw for $g_1^{*}$
. As we saw for $g_1^{*}$![]() , Lemma 5.3 and Lemma 5.1 deal respectively with the cases that $(1)h_2^{-1}$
, Lemma 5.3 and Lemma 5.1 deal respectively with the cases that $(1)h_2^{-1}$![]() is even or odd. We now note that if $1$
is even or odd. We now note that if $1$![]() and $3$
and $3$![]() lie on distinct $g_2$
lie on distinct $g_2$![]() orbits and there are no such $a,\, b\in \operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$
orbits and there are no such $a,\, b\in \operatorname {supp}(g_2)\setminus \{c,\, x,\, y\}$![]() which lie on the same orbit of $g_2$
which lie on the same orbit of $g_2$![]() , then we have one of a finite list of cases. We end by dealing with each such possibility.
, then we have one of a finite list of cases. We end by dealing with each such possibility.
If $x,\, y\not \in \operatorname {supp}(g_2)$![]() , then $|\operatorname {supp}(g_2)|\geqslant 3$
, then $|\operatorname {supp}(g_2)|\geqslant 3$![]() and so there exist $a,\, b\in \operatorname {supp}(g_2)\setminus \{c\}$
and so there exist $a,\, b\in \operatorname {supp}(g_2)\setminus \{c\}$![]() that lie on the same orbit of $g_2$
that lie on the same orbit of $g_2$![]() . If $x\in \operatorname {supp}(g_2)$
. If $x\in \operatorname {supp}(g_2)$![]() but $y\not \in \operatorname {supp}(g_2)$
but $y\not \in \operatorname {supp}(g_2)$![]() , then either:
, then either:
• $g_2^{\omega }$
 or its inverse equals $(i\;0\;1)$
or its inverse equals $(i\;0\;1)$ for some $i\in \mathbb {Z}\setminus \{0,\, 1\}$
for some $i\in \mathbb {Z}\setminus \{0,\, 1\}$ , in which case, by choosing the appropriate $\omega$
, in which case, by choosing the appropriate $\omega$ , we can set $i:=-1$
, we can set $i:=-1$ so that $\langle g_2^{\omega },\, t^{2}\rangle =G_2$
so that $\langle g_2^{\omega },\, t^{2}\rangle =G_2$ ; or
; or• $g_2^{\omega }=(i\;0)(j\;1)$
 for some distinct $i,\, j\in \mathbb {Z}\setminus \{0,\, 1\}$
for some distinct $i,\, j\in \mathbb {Z}\setminus \{0,\, 1\}$ . We set $i:=-5$
. We set $i:=-5$ and $j:=-1$
and $j:=-1$ and note that $\langle g_2^{\omega },\, t^{2}\rangle$
and note that $\langle g_2^{\omega },\, t^{2}\rangle$ contains $g_2^{\omega }((t^{-2}g_2^{\omega } t^{2})^{-1}g_2^{\omega }(t^{-2}g_2^{\omega } t^{2}))=(-1\;1\;3)$
contains $g_2^{\omega }((t^{-2}g_2^{\omega } t^{2})^{-1}g_2^{\omega }(t^{-2}g_2^{\omega } t^{2}))=(-1\;1\;3)$ . We can then apply Lemma 5.1 to the orbit of $t^{2}$
. We can then apply Lemma 5.1 to the orbit of $t^{2}$ containing $2\mathbb {Z}+1$
containing $2\mathbb {Z}+1$ in order to generate $\operatorname {Alt}(2\mathbb {Z}+1)$
in order to generate $\operatorname {Alt}(2\mathbb {Z}+1)$ , and then apply Lemma 6.4 for our desired conclusion that $\langle g_2^{\omega },\, t^{2}\rangle =G_2$
, and then apply Lemma 6.4 for our desired conclusion that $\langle g_2^{\omega },\, t^{2}\rangle =G_2$ .
.
We commented above that we could assume that if $y\in \operatorname {supp}(g_2)$![]() , then $x$
, then $x$![]() must also be in $\operatorname {supp}(g_2)$
must also be in $\operatorname {supp}(g_2)$![]() . So finally, if $x,\, y \in \operatorname {supp}(g_2)$
. So finally, if $x,\, y \in \operatorname {supp}(g_2)$![]() , then $g_2^{\omega }$
, then $g_2^{\omega }$![]() or its inverse is either $(i\;1\;0)(j\;3)$
or its inverse is either $(i\;1\;0)(j\;3)$![]() , $(i\;0\;3)(j\;1)$
, $(i\;0\;3)(j\;1)$![]() , or $(i\;0)(j\;1)(k\;3)$
, or $(i\;0)(j\;1)(k\;3)$![]() . But then $g_2\not \in \operatorname {Alt}(\mathbb {Z})$
. But then $g_2\not \in \operatorname {Alt}(\mathbb {Z})$![]() , since these are all odd permutations.
, since these are all odd permutations.
We are now equipped to show that $u(G_2)\geqslant 2$![]() , which we approach in a similar way to the proof of Lemma 6.3.
, which we approach in a similar way to the proof of Lemma 6.3.
Lemma 6.6 The group $G_2$![]() has uniform spread at least 2.
has uniform spread at least 2.
Proof. Let $g_1,\, g_2 \in G_1$![]() . We will show that there exists $\alpha \in \operatorname {FSym}(\mathbb {Z})$
. We will show that there exists $\alpha \in \operatorname {FSym}(\mathbb {Z})$![]() such that $\langle s_\alpha ^{2},\, g_1\rangle = \langle s_\alpha ^{2},\, g_2\rangle =G_2$
such that $\langle s_\alpha ^{2},\, g_1\rangle = \langle s_\alpha ^{2},\, g_2\rangle =G_2$![]() . If $g_1,\, g_2 \in G_2\setminus \operatorname {Alt}(\mathbb {Z})$
. If $g_1,\, g_2 \in G_2\setminus \operatorname {Alt}(\mathbb {Z})$![]() , then Theorem 4.4 implies the result. If $g_1 \in \operatorname {Alt}(\mathbb {Z})$
, then Theorem 4.4 implies the result. If $g_1 \in \operatorname {Alt}(\mathbb {Z})$![]() and $g_2\in G_2\setminus \operatorname {Alt}(\mathbb {Z})$
and $g_2\in G_2\setminus \operatorname {Alt}(\mathbb {Z})$![]() , then we can apply Lemma 5.4 in the same way to how Lemma 5.2 is used in the proof of Lemma 6.3. The final case was dealt with in the previous proposition.
, then we can apply Lemma 5.4 in the same way to how Lemma 5.2 is used in the proof of Lemma 6.3. The final case was dealt with in the previous proposition.
In light of Theorem 4.4, we consider a finite collection of elements in $\operatorname {Alt}(\mathbb {Z})$![]() to obtain upper bounds on the spread of $G_1$
to obtain upper bounds on the spread of $G_1$![]() and $G_2$
and $G_2$![]() . I thank François Le Maître for his improvements to the following argument.
. I thank François Le Maître for his improvements to the following argument.
Lemma 6.7 The group $G_1$![]() has spread at most 9.
has spread at most 9.
Proof. We will construct a set $S\subset G_1$![]() , of size 10, such that no $h\in G_1$
, of size 10, such that no $h\in G_1$![]() generates $G_1$
generates $G_1$![]() with every element in $S$
with every element in $S$![]() . The set will consist of $3$
. The set will consist of $3$![]() -cycles in $\operatorname {Alt}(\mathbb {Z})$
-cycles in $\operatorname {Alt}(\mathbb {Z})$![]() with support contained within $X=\{1,\, \ldots,\, 5\}$
with support contained within $X=\{1,\, \ldots,\, 5\}$![]() and chosen such that if $\sigma \in S$
and chosen such that if $\sigma \in S$![]() then $\sigma ^{-1}\not \in S$
then $\sigma ^{-1}\not \in S$![]() . There are $\binom {5}{3}=10$
. There are $\binom {5}{3}=10$![]() such cycles. Let $h\in G_1$
such cycles. Let $h\in G_1$![]() . Then $h=\sigma t^{k}$
. Then $h=\sigma t^{k}$![]() for some $\sigma \in \operatorname {Alt}(\mathbb {Z})$
for some $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() and $k\in \mathbb {Z}$
and $k\in \mathbb {Z}$![]() . If $k\not \in \{1,\, -1\}$
. If $k\not \in \{1,\, -1\}$![]() , then $h$
, then $h$![]() cannot generate $G_1$
cannot generate $G_1$![]() with $(1\;2\;3)$
with $(1\;2\;3)$![]() .
.
We start with the observation that, given 5 points in $\mathbb {Z}$![]() , they cannot all lie on the infinite orbit of $h$
, they cannot all lie on the infinite orbit of $h$![]() . To do this, we use Lemma 5.1. Assume that $h$
. To do this, we use Lemma 5.1. Assume that $h$![]() consists of a single infinite orbit, equal to $\mathbb {Z}$
consists of a single infinite orbit, equal to $\mathbb {Z}$![]() . Without loss of generality, reorder $\mathbb {Z}$
. Without loss of generality, reorder $\mathbb {Z}$![]() so to replace $h$
so to replace $h$![]() with $t$
with $t$![]() , the translation map. Now, given $\{a,\, b,\, c,\, d,\, e\}\subset \mathbb {Z}$
, the translation map. Now, given $\{a,\, b,\, c,\, d,\, e\}\subset \mathbb {Z}$![]() with $a< b< c< d< e$
with $a< b< c< d< e$![]() , at least 3 of these points lie in $2\mathbb {Z}$
, at least 3 of these points lie in $2\mathbb {Z}$![]() or in $2\mathbb {Z}+1$
or in $2\mathbb {Z}+1$![]() . Let $\sigma$
. Let $\sigma$![]() denote the 3-cycle with support equal to 3 such points. Lemma 5.1 then states that $\langle \sigma,\, t\rangle \ne G_1$
denote the 3-cycle with support equal to 3 such points. Lemma 5.1 then states that $\langle \sigma,\, t\rangle \ne G_1$![]() .
.
From the previous paragraph, no $h$![]() with an infinite orbit equal to $\mathbb {Z}$
with an infinite orbit equal to $\mathbb {Z}$![]() can generate $G_1$
can generate $G_1$![]() with each element from $S$
with each element from $S$![]() . Hence at least one of $\{1,\, \ldots,\, 5\}$
. Hence at least one of $\{1,\, \ldots,\, 5\}$![]() must lie on a finite orbit of $h$
must lie on a finite orbit of $h$![]() . Let $K$
. Let $K$![]() be the intersection of the infinite orbit of $h$
be the intersection of the infinite orbit of $h$![]() with $\{1,\, \ldots,\, 5\}$
with $\{1,\, \ldots,\, 5\}$![]() , and let $L:=\{1,\, \ldots,\, 5\}\setminus K$
, and let $L:=\{1,\, \ldots,\, 5\}\setminus K$![]() . One of $K$
. One of $K$![]() or $L$
or $L$![]() must have size 3, and so contains $m_1< m_2< m_3$
must have size 3, and so contains $m_1< m_2< m_3$![]() from $\{1,\, \ldots,\, 5\}$
from $\{1,\, \ldots,\, 5\}$![]() . Let $\omega =(m_1\;m_2\;m_3)$
. Let $\omega =(m_1\;m_2\;m_3)$![]() . Then $\langle h,\, \omega \rangle \ne G_1$
. Then $\langle h,\, \omega \rangle \ne G_1$![]() since the group generated by $h$
since the group generated by $h$![]() and $\omega$
and $\omega$![]() does not act transitively on $\mathbb {Z}$
does not act transitively on $\mathbb {Z}$![]() .
.
Lemma 6.8 The group $G_2$![]() has spread at most 9.
has spread at most 9.
Proof. As with the previous proof, let $S$![]() consist of those $3$
consist of those $3$![]() -cycles in $\operatorname {Alt}(\mathbb {Z})$
-cycles in $\operatorname {Alt}(\mathbb {Z})$![]() with support contained within $X=\{1,\, \ldots,\, 5\}$
with support contained within $X=\{1,\, \ldots,\, 5\}$![]() and chosen such that if $\sigma \in S$
and chosen such that if $\sigma \in S$![]() then $\sigma ^{-1}\not \in S$
then $\sigma ^{-1}\not \in S$![]() . We will show that no $h\in G_2$
. We will show that no $h\in G_2$![]() generates $G_2$
generates $G_2$![]() with every element in $S$
with every element in $S$![]() . Given $h\in G_2$
. Given $h\in G_2$![]() , we have that $h=\sigma t^{2k}$
, we have that $h=\sigma t^{2k}$![]() where $\sigma \in \operatorname {Alt}(\mathbb {Z})$
where $\sigma \in \operatorname {Alt}(\mathbb {Z})$![]() and $k \in \mathbb {Z}$
and $k \in \mathbb {Z}$![]() . If $k\not \in \{1,\, -1\}$
. If $k\not \in \{1,\, -1\}$![]() , then $h$
, then $h$![]() cannot generate $G_2$
cannot generate $G_2$![]() with $(1\;2\;3)$
with $(1\;2\;3)$![]() . Let $h$
. Let $h$![]() have infinite orbits $\mathcal {O}_1$
have infinite orbits $\mathcal {O}_1$![]() and $\mathcal {O}_2$
and $\mathcal {O}_2$![]() and define $\phi _h: X\rightarrow \{0,\, 1,\, 2\}$
and define $\phi _h: X\rightarrow \{0,\, 1,\, 2\}$![]() by
by
• $0$
 if $x$
if $x$ lies on a finite orbit of $h$
lies on a finite orbit of $h$ ;
;• $1$
 if $x\in \mathcal {O}_1$
if $x\in \mathcal {O}_1$ ; and
; and• $2$
 if $x\in \mathcal {O}_2$
if $x\in \mathcal {O}_2$ .
.
It is clear that the image of $\phi$![]() must contain $\{1,\, 2\}$
must contain $\{1,\, 2\}$![]() , since otherwise $\langle h,\, (a\;b\;c)\rangle$
, since otherwise $\langle h,\, (a\;b\;c)\rangle$![]() cannot act transitively on both $\mathcal {O}_1$
cannot act transitively on both $\mathcal {O}_1$![]() and $\mathcal {O}_2$
and $\mathcal {O}_2$![]() for any distinct $a,\, b,\, c\in X$
for any distinct $a,\, b,\, c\in X$![]() . Similarly, we cannot have two points of $X$
. Similarly, we cannot have two points of $X$![]() sent to 0 by $\phi$
sent to 0 by $\phi$![]() , and we cannot have 3 points of $X$
, and we cannot have 3 points of $X$![]() sent to either 1 or to 2. Thus, after relabelling, the only possibility is that $\phi (1)=0$
sent to either 1 or to 2. Thus, after relabelling, the only possibility is that $\phi (1)=0$![]() , $\phi (2)=\phi (3)=1$
, $\phi (2)=\phi (3)=1$![]() , and $\phi (4)=\phi (5)=2$
, and $\phi (4)=\phi (5)=2$![]() . But then $\langle h,\, (1\;2\;3)\rangle \ne G_2$
. But then $\langle h,\, (1\;2\;3)\rangle \ne G_2$![]() .
.
Acknowledgements
I thank Scott Harper of the University of Bristol for his illuminating talks, ever-keen interest to discuss group theory, and comments on this work. I also thank both him and Casey Donoven for the interesting questions they raised in [Reference Donoven and Harper13]. I thank the anonymous referees for their comments. I thank François Le Maître, Université de Paris, for his improvements to Lemma 6.7. Finally, I thank Tim Burness of the University of Bristol for his support and encouragement.
Competing interests
The author is employed by the University of Bristol.