Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:09:03.805Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of eigenvalues in the spectral gap of a Dirac system

Published online by Cambridge University Press:  20 January 2009

D. B. Hinton ,
A. B. Mingarelli ,
T. T. Read  and
J. K. Shaw
D. B. Hinton
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996
A. B. Mingarelli
Affiliation:
Mathematics Department, University of Ottawa, Ottawa, Ontario K1N 6N5
T. T. Read
Affiliation:
Mathematics Department, Western Washington University, Bellingham, WA 98225
J. K. Shaw
Affiliation:
Mathematics Department, Virginia Tech, Blacksburg, VA 24061
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the one-dimensional operator,

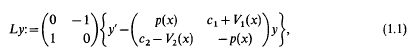
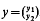on 0<x<∞ with . The coefficients p, V1 and V2 are assumed to be real, locally Lebesgue integrable functions; c1 and c2 are positive numbers. The operator L acts in the Hilbert space H of all equivalence classes of complex vector-value functions 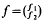such that 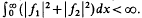. L has domain D(L) consisting of ally∈H such that y is locally absolutely continuous and Ly∈H; thus in the language of differential operators L is a maximal operator. Associated with L is the minimal operator L0 defined as the closure of 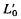where 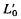is the restriction of L to the functions with compact support in (0,∞).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 3 , October 1986 , pp. 367 - 378
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Behncke, H., The Dirac equations with an anomalous magnetic moment, II, Lecture Notes in Mathematics 964, pp. 77–85 (Springer, Berlin-Heidelberg-New York, 1982).Google Scholar
2.Behrens, H. and Buhring, W., Electron radial wave functions and nuclear beta-decay (Clarendon Press, Oxford, 1982).Google Scholar
3.Birman, M. S., The spectra of singular boundary problems, Matem. Sbornik 55 (1961), 125–174;Google Scholar
Amer. Math. Soc. Translations 53 (1966), 23–80.CrossRefGoogle Scholar
4.Coppel, W. A., Stability and asymptotic behavior of differential equations (Heath, Boston, 1965).Google Scholar
5.Dunford, N. and Schwarz, J., Linear Operators, Part I (Interscience, New York, 1958).Google Scholar
6.Etgen, G. J. and Pawlowski, J. F., Oscillation criteria for second order self-adjoint differential systems, Pacific J. Math. 66 (1976), 99–110.CrossRefGoogle Scholar
7.Glazman, I. M., Direct methods of qualitative spectral analysis of singular differential operators (Israel program for scientific translation, Jerusalem, 1965).Google Scholar
8.Hinton, D. and Shaw, J. K., Absolutely continuous spectra of Dirac systems with long range, short range, and oscillating potentials, Quart. J. Math. (2), 36 (1985), 183–213.CrossRefGoogle Scholar
9.Hinton, D. and Shaw, J. K., Spectral properties of a separated Dirac operator (preprint).Google Scholar
10.Hinton, D. and Shaw, J. K., Dirac systems with discrete spectra, Canad. J. Math., to appear.Google Scholar
11.Kalf, H., A limit-point criterion for separated Dirac operators and a little known result on Riccati's equation, Math. Z. 129 (1972), 75–82.CrossRefGoogle Scholar
12.Kalf, H., Schmincke, U.-W., Walter, J. and Wust, R., On the spectral theory of Schrodinger and Dirac operators with strongly singular potentials, Lecture Notes in Mathematics 448, pp. 182–226 (Springer, Berlin-Heidelberg-New York, 1975).Google Scholar
13.Klaus, M., On the point spectrum of Dirac operators, Helv. Phy. Ada. 53 (1980), 453–162.Google Scholar
14.Klaus, M. and Wust, R., Spectral properties of Dirac operators with singular potentials, J. Math. Anal. Appl. 72 (1979), 206–214.CrossRefGoogle Scholar
15.Kurbenin, O. I., The discrete spectra of the Dirac and Pauli operators, Topics in Mathematical Physics 3, pp. 43–52 (Consultants Bureau, New York-London, 1969).Google Scholar
16.Lewis, R. T., Conjugate points of vector-matrix differential equations, Trans. Amer. Math. Soc. 231 (1977), 167–178.CrossRefGoogle Scholar
17.Lewis, R. T. and Wright, L. C., Comparison and oscillation criteria for selfadjoint vector matrix differential equations, Pacific J. Math. 90 (1980), 125–134.CrossRefGoogle Scholar
18.Levitan, B. M. and Sargsjan, I., Introduction to spectral theory: Selfadjoint ordinary differential operators. Translations of Mathematical Monographs 39 (Amer. Math. Soc, Providence, 1975).CrossRefGoogle Scholar
19.Read, T. T., Elliptic equations without positive solutions, J. Diff. Eqs. 58 (1985), 381–390.CrossRefGoogle Scholar
20.Schmincke, U. W., Distinguished selfadjoint extensions of Dirac operators, Math. Z. 129 (1972), 335–349.CrossRefGoogle Scholar
21.Tamura, H., The asymptotic distribution of discrete eigenvalues for Dirac systems, J. Fac. Sci. U. Tokyo 23 (1976), 167–197.Google Scholar
22.Titchmarsh, E. C., On the nature of the spectrum in problems of relativistic quantum mechanics, Quart. J. Math. (2) 12 (1961), 227–240.CrossRefGoogle Scholar
23.Weidmann, J., Oscillationsmethoden fur Systeme gewohnlicher Differentialgleichungen, Math. Z. 119 (1971), 349–373.CrossRefGoogle Scholar
24.Wust, R., Dirac operators with strongly singular potentials, Math. Z. 152 (1977), 259–271.CrossRefGoogle Scholar