Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-06T07:22:39.136Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Evaluation of Determinants, the Formation of their Adjugates, and the Practical Solution of Simultaneous Linear Equations

Published online by Cambridge University Press:  20 January 2009

A. C. Aitken
A. C. Aitken
Affiliation:
Edinburgh University.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are various methods in existence for the practical solution of a set of simultaneous equations

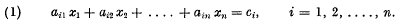
Some of these methods are appropriate to special systems, as for example to the axisymmetric “normal equations” of Least Squares. In many applications, however, as in problems of statistical correlation of many variables, it may be desired not merely to solve a given set of equations but to obtain as much knowledge as possible about the system or matrix of coefficients; perhaps to evaluate its determinant and various minors, such as principal minors, possibly also to determine the elements of the adjugate matrix, or the reciprocal matrix. The examination of the sign of successive principal minors of an axisymmetric determinant, in order to find the signature of the corresponding quadratic form, is a case in point; and there are many such applications.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , Issue 3 , February 1933 , pp. 207 - 219
Copyright
Copyright © Edinburgh Mathematical Society 1933

References

page 208 note 1 According to which the minor, e.g. arising from the 1st, 3rd and 4th rows, and Und, 5th and 6th columns, is represented by

page 208 note 2 Werke VI, 18–24;Google Scholar see also Bertrand's translation in his Méthode des Moindres Carrés, 139–141.Google Scholar

page 209 note 1 Phil. May. (3), 18 (1927), 1007.Google Scholar

page 209 note 2 An extension, i.e. added letters and suffixes, can of course be inserted not merely at the end, as |a 1b 2 becoming | a 1b 2c 3d 4|, but in the middle or elsewhere, as | a 1d 4 | becoming | a 1b 2c 3d 4 |.

page 211 note 1 If the original determinant is of less than full rank, we shall come to a stage in which all entries are zero. CfRice, L. H.Journ. Math. and Phys. (Massachusetts), 11 (1932), 146–149.CrossRefGoogle Scholar

page 211 note 2 Cf. § 5, infra. This rule of sign differs from that given by the author in a very similar method for computing determinants, Trans. Fac. Act., 13 (1931), 272–275.Google Scholar

page 215 note 1 CfEtherington, I. M. H., in Proc. Edin. Math. Soc. (2), 3 (1932), 107–117.CrossRefGoogle Scholar

page 217 note 1 CfTurnbull, Determinants, Matrices and Invariants, 77–79.Google Scholar

page 218 note 1 Muir, History of Determinants, Vol I, Part I, p. 172.Google Scholar