Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:43:17.968Z Has data issue: false hasContentIssue false
  • English
  • Français

On spreads in PG(3,2s) that admit projective groups of order 2s

Published online by Cambridge University Press:  20 January 2009

V. Jha  and
N. L. Johnson
V. Jha
Affiliation:
Department of Mathematics, The University of Iowa, Iowa City, Iowa 52242, U.S.A.
N. L. Johnson
Affiliation:
Mathematics Department, Glasgow College of Technology, Cowcaddens Road, Glasgow G4 0BA, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Γ be a spread in 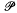= PG(3, q); thus Γ consists of a set of q2 +1 mutually skew lines that partition the points of 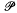. Also let Λ be the group of projectivities of 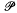that leave Γ invariant: so Λ is the “linear translation complement” of Γ, modulo the kern homologies. Recently, inspired by a theorem of Bartalone [1], a number ofresults have been obtained, in an attempt to describe (Γ, Λ) when q2 divides |Λ|. A good example of such a result is the following theorem of Biliotti and Menichetti [3], which ultimately depends on Ganley's characterization of likeable functions of even characteristic [5].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 3 , October 1985 , pp. 355 - 360
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Bartalone, C., On some translation planes admitting a Frobenius group of collineations, Combinatorics '81, Annals Discr. Math. 18 (1983), 37–54.Google Scholar
2.Betten, D., 4-dimensional Translationsebenen mit 8-dimensionaler Kollineations-gruppe, Geom. Ded. 2 (1973), 327–339.CrossRefGoogle Scholar
3.Biliotti, M. and Menichetti, G., On a genralization of Kantor's likeable planes. Geom. Ded. 17 (1985), 253–277.CrossRefGoogle Scholar
4.Dempfwolff, U., Grosse Baer-Untergruppen auf translationsebenen gerader Ordnung, J. Geometry 19 (1982), 101–114.CrossRefGoogle Scholar
5.Ganley, M. J., On likeable translation planes of even order, Arch. Math. 41 (1983), 478–480.CrossRefGoogle Scholar
6.Hughes, D. R. and Piper, F. C., Projective Planes (Springer-Verlag, New York/Heidelberg/Berlin, 1973).Google Scholar
7.Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin/New York, 1967).CrossRefGoogle Scholar
8.Jha, V., Johnson, N. L. and Wilkie, F. W., On translation planes of order q2 that admit a group of order q\q — 1); Bartalone's theorem, Rendiconti Circolo Mat. Palermo, 33 (1984), 407–424.CrossRefGoogle Scholar
9.Johnson, N. L. and Ostrom, T. G., Translation planes of characteristic two in which all involutions are Baer, J. Algebra 54 (1978), 447–458.CrossRefGoogle Scholar
10.Johnson, N. L. and Wilkie, F. W., Translation planes of order q2 that admit a collineation group of order q2, Geom. Dedicata 3 (1984), 293–312.Google Scholar
11.Loneburg, H., Translation Planes (Springer-Verlag, Berlin/Heidelberg/New York, 1980).CrossRefGoogle Scholar